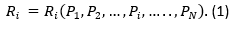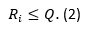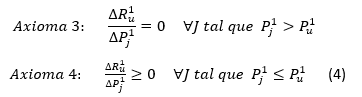Original article

The Possibility of Classifying for the World Cup and Its Mathematical Rationale

0000-0002-6643-8940Fernando Correa Alsina^{1  *} 

¹Universidad de la República, Regional Norte, Facultad de Ciencias Sociales Salto, Uruguay

Abstract

This article presents a method which allows to determine whether a national soccer team which is participating in the qualifying phase for the World Cup has a mathematical chance of achieving the passage to the final phase of said competition. The method is based on axioms developed for these purposes and its operation is illustrated by applying it to a specific case corresponding to the South American Qualifiers. This method is efficient, rigorous, flexible and applicable to a wide range of situations.

Key words: Qualifiers; World cup; Soccer; Mathematical chance.

Introduction

Every four years and almost uninterruptedly since 1930, the Men’s Soccer World Cup is organized by the International Federation of Association Football (FIFA). All national selections look to participate in this event that gathers the interest of the public and media coverage for the thirty days of the tournament. However, only a limited number of nations make it to the World Cup. It is worth mentioning that of the 210 representatives that take part in the qualifications for the World Cup of Qatar 2022, only 31 will be present, along with the host country in the final part of the tournament ^{(FIFA, 2021)}.

The qualifying round has also changed through time, and it varies according to the geographical area. However, it has maintained two features that confer it certain uniqueness. Firstly, the qualifications are held in every continent, and therefore, matches between historically known opponents are frequent. Secondly, they are organized as first and second legs, with crowds of locals in stadiums, fans that find a symbol of collective identity in the t-shirts of the national selection ^{(Galeano, 1995, 230)}. These factors determine that the participants feel greater pressure when they compete to get the qualification for the final stage of the tournament.

Soccer players and coaches who have participated in the qualifying games recall them as very demanding and exhausting competitions lived through a lot of pressure. The combination of adverse results and the huge pressure withstood frequently lead to the dismissal or resignation of coaches. On the contrary, qualifying for the final phase reports great satisfaction mixed with a sensation of relieve, then everything is quickly forgotten. In short, the qualifying games never represent a feeling of happiness and celebration lived during the World Cup ^{(Alabarces et al., 2018, 41}; ^{Bassorelli, 2014, 239}; ^{Castillo and Varoli, 2013, 146-147}; ^{Rivas and Señorans, 2003, 52-53)}.

The fans and related press members also live the qualifying phase with special intensity. Shortly before the end, everyone makes estimations and speculate about the possibilities of the national selection of classifying to the next World Cup. Various analyses refer to two different aspects that are interrelated. On one hand, they try to determine the mathematical probabilities of classifying . On the other, they express certain probability to participate in the event, either subjectively or based on certain rationale. While the former admits a single correct response, the latter is just judgement. Although this distinction is clear, the way the media handles it is misleading. The solidity of certain assertions, frequently made after an adverse sports result that plunges the national selection in the final tournament positions, can create the idea that there are no mathematical possibilities of qualifying for the World Cup, when sometimes reality shows that, in the best of cases, the predictions were mistaken ^{Piñón, 2009, 4}; ^{Savia, 2009, 2}; ^{Señorans, 2009, 2)}.

This paper shows a method to make an accurate determination if a national selection taking part in the qualifications has a chance to participate in the World Cup, regardless of the stage of the competition. This method is formulated and explained mathematically in the section below. In the third section, it is applied to a concrete case of the past; in the fourth section the same case is discussed, and the variants are analyzed; the last section shows the conclusions.

Materials and methods

The method presented in this article is explained through some elemental mathematical concepts associated with the properties of inequalities ^{(Kalnin, 1973}, 46-48), the incremental ^{(Woods and Bailey, 1944, 135)} and differential ^{(Chiang, 1996, 194-196)} calculus.

Notation

The qualifying stage of the World Cup is a competition between N countries in which the national selections ranking in the first Q positions win their ticket for the World tournament, being Q the quota given by FIFA to that set of representing teams.

The position of a particular country i in the position (R _i ) at any time of the competition is a function of the points scored by that selection (Pi) and the other teams (P _j ) (Equation 1).

Number 1 is given to the first position (R _i =1); 2, to the second (Ri=1); and successively, qualifying all the teams that meet the following condition at the end of the competition (Equation 2).

Method

In order to determine if a country, identified with letter U, has mathematical probabilities to qualify for the World Cup when there are still a few games left to play in the qualifications, the games should be given results that permit them to obtain the best possible position of U in the positions at the end of this phase. If after this U is still in the first Q positions, then qualifying will be possible, not otherwise.

The results of the pending matches should be given in this order: the instructions foreseen in the first five steps, regardless of the chronological order of the games, until all the steps have been completed. At the end of each step, the points won by country and the positions should be updated, in order to use them in the next step. From that time on, the corresponding updated information of the score and the standings will be identified with the highest corresponding index.

First step

The victories should be assigned to country U in all the games to be played. In turn, U will win those victories by a goal difference that permits the team to overtake every country position, from now on having the same score.

The position of U will improve or stay the same under this procedure (Axiom 1), and at the same time, it will be the same or better than if other results are assigned to the same games (Axioms 1 and 2) (Equation 3).

Second step

Secondly, the victories should be given in all the games they take part and still one more result needs to be added to the countries that, according to the updated positions, have a higher ranking than U. In case there are crossings between two countries, any results could be assigned to such matches.

The position of U in the standings will remain unchangeable under this procedure (Axiom 3), and at the same time, it will be the same or better than if other results are assigned to the same games (Axioms 3 and 4) (Equation 4).

Third step

In the third place, the victories should be given, in all the games they take part and still one more result needs to be added, to the countries that, according to the updated positions, rank below U, provided that winning all those games will not offer them better indicators. In case of crossings between countries that are unable to defeat U after winning all their games, any results could be given to such matches.

The position of U in the ranking will remain unchangeable under this procedure (Axiom 5), and at the same time, it will be the same or better than if other results are assigned to the same games (Axioms 5 and 6) (Equation 5).

This step should be implemented carefully, trying to avoid assigning victories to countries that, having the same number of victories, reach a lower score than U, but wining their remaining games can climb higher in the ranking, which would lead to a drop of U in the updated standings, as inferred from axiom 6.

Fourth step

After the third step, other countries that did not seem to have the conditions expected may appear to meet such conditions now, since the number of matches waiting for results has been shortened. Therefore, the instructions corresponding to the previous step will be applicable recurrently until no new countries that meet these conditions emerge.

Again, the position of U in the standings will remain unchangeable under this procedure (Axiom 5), and at the same time, it will be the same or better than if other results are assigned in the same games (Axioms 5 and 6).

Following the allocation of results that correspond to any of the four steps, the full timetable will possible be completed, and therefore, the final positions will correspond to them. In this case, if according to the table the possible qualification of U to the World Cup is verified by R_u^i≤Q not otherwise R_u^i>Q. On the contrary, if there are still some matches to hold and no results have been assigned, the fifth step should be carried out.

Fifth step

The pending matches that still have no results assigned correspond exclusively to crossings between countries that, according to the updated positions, have a lower score than U, and could climb higher in the rankings, provided that they win all the points corresponding to the games to be assigned.

Three possible results must be assignedin these matches (victory of I, victory of J, and tie). Combining the results from the different games (q), there will be 3 ^q different final positions. Among them, the one in which U takes the best position will be identified, then the existence of conditions for possible qualification will be verified (Equation 6).

As can be seen, the method is first oriented to place U in the best possible ranking in the updated positions. Hence, it is clear that victories must be attributed to that particular country in all their games by a goal margin that sets it above any opponent in case they have the same points.

The next steps of the method permit the completion of the timetable, and preventing that U drops in the updated standings. It can be achieved, on one hand, by attributing victories to the countries in a higher position than U; and on the other, the countries below that cannot reach it. Note that the order in which the steps are taken is critical for the effectiveness of the method. In fact, the third step will be more effective if the other two have been taken before, and in turn, the fourth step derives from the third.

Method application

Between October 2007 and October 2009, the South American Qualifiers for the FIFA World Cup South Africa 2010 took place. The qualifying competition consisted in a double round robin tournament among the ten countries involved. The first four won a direct ticket to the World Cup, the fifth had to face the fourth place in the Central and North America qualifiers for an additional quota.

Having four games to the finals, Uruguay was in sixth position, and was supposed to play Peru as a visiting team. The team players were united and supported their technical management, despite the harsh criticism from the press ^{Lissardy, 2011, 461)}. A victory over Lima seemed an extremely urgent task to fulfill to have a chance of qualifying for the World Cup.

However, the outcome was unfavorable to Uruguay. The defeat by a point against Peru sent Uruguay to the seventh position in the rankings, it was a sharp blow to players and fans. The national media considered the selection had no single chance of qualifying to the World Cup. The opinions given by the main diaries of the country were clear in that respect: “Let the South African FIFA World Cup be bygone. May time go fast.” ^{(Piñón, 2009, 4)}; “Peru again (...) leaves us out” ^{(Señorans, 2009, 2)}; “Peru put an end to the dream. Uruguay lost its chance of qualifying after losing to the last in the ranking” ^{(Savia, 2009, 2)}.

Contrary to what the previous assertions seemed to suggest, Uruguay still had a chance of qualifying for the World Cup, even after losing in Lima. Following is the method presented in the previous section to show this conclusion could be made based on the information available then ^{(Asociación Uruguaya de Fútbol, 2015}; ^{FBREF, 2010a} y ^{FBREF, 2010b)}.

Information available

During the first fifteen days of the qualifying tournament, Uruguay had only scored eighteen points, and ranked seventh, out of the qualification zone, overtaking Venezuela by goal difference (+6 against -7), behind Brazil, Chile, Paraguay, Argentina, Colombia, and Ecuador. In the three remaining games, Colombia was visiting Ecuador, and would play Argentina as a home team (Table 1).

Table 1.  - South American Qualifiers for the FIFA World Cup, 2010, standings and last scheduled games 

Game No 16	Game No 17	Game No 18
Home-Visiting team	Home-Visiting team	Home-Visiting team
Bolivia - Ecuador	Colombia - Chile	Perú - Bolivia
Uruguay - Colombia	Venezuela - Paraguay	Brazil - Venezuela
Paraguay - Argentina	Ecuador - Uruguay	Chile - Ecuador
Brazil - Chile	Argentina - Perú	Uruguay - Argentina
Venezuela - Perú	Bolivia - Brazil	Paraguay - Colombia
Standings after Game No 15: 1 °) Brazil 30 points; 2 °) Chile points; 3°) Paraguay 27 points; 4°) Argentina 22 points; 5°) Colombia 20 points;	6°) Ecuador 20 points; 7°) Uruguay 18 points; 8°) Venezuela 18 points;	9°) Bolivia 12 points; 10°) Perú 10 poiunts.

First step

In order to maximize the score that Uruguay could reach at the end of the qualifying tournament, first, a number of victories are allocated to the sky-blue team in the last three games of the competition. Likewise, the victories must have a goal difference big enough to ensure a favorable definition in case a tie occurs with any other opponent. As will be seen later, in this particular case, the goal difference is not determinant.

Upon updating the positions with the results of this allocation, Uruguay climbed to the second position, with a total of 27 points, equaling Chile and Paraguay, but having a better goal balance than the two other teams (Table 2).

Table 2.  - Results allocated in the first step and updated standings 

Game No 16	Game No 17	Game No 18
Uruguay defeats Colombia	Uruguay defeats Ecuador	Uruguay defeats Argentina
Updated standings after the first step: 1 °) Brazil 30 points; 2°) Uruguay 27 points; 3°) Chile 27 points; 4°) Paraguay 27 points;	5°) Argentina 22 points; 6°) Colombia 20 points; 7°) Ecuador 20 points;	8°) Venezuela 18 points; 9°) Bolivia 12 points; 10°) Perú 10 points.

Second step

After the second step, Brazil is the only country above Uruguay in the updated positions chart. Therefore, since Brazil was unreachable it received the victories in its three final games against Bolivia, Chile, and Venezuela, accumulating 39 points at the end of qualifiers (Table 3).

Table 3.  - Results allocated in the second step and updated standings 

Game No 16	Game No 17	Game No 18
Brazil defeats Chile	Brazil defeats Bolivia	Brazil defeats Venezuela
Updated standings after the second step: 1°) Brazil 39 points; 2°) Uruguay 27 points; 3°) Chile 27 points; 4°) Paraguay 27 points;	5°) Argentina 22 points; 6°) Colombia 20 points; 7°) Ecuador 20 points;	8°) Venezuela 18 points; 9°) Bolivia 12 points; 10°) Perú 10 points.

Third step

Upon finalizing the second step, five countries were unable to reach the score of Uruguay, considering the remaining games, as well as those with no outcome allocated, namely, Bolivia, Colombia, Ecuador, Peru, and Venezuela. The victories were conceded to Uruguay in the next matches, except where they played against each other. In such cases, any outcome can be allocated, so the choice was to concede a tie. After this allocation, Uruguay maintained the second position in the rankings (Table 4).

Table 4.  - Results allocated in the third step and updated standings 

Game No 16	Game No 17	Game No 18
Bolivia has a tie with Ecuador	Colombia defeats Chile	Bolivia has a tie with Peru
Perú has a tie with Venezuela	Venezuela defeats Paraguay	Ecuador defeats Chile
--	Perú defeats Argentina	Venezuela defeats Paraguay
Updated standings after the third step: 1°) Braxil 39 points; 2°) Uruguay 27 points; 3°) Chile 27 points; 4°) Paraguay 27 points;	5°) Colombia 26 points; 6°) Ecuador 24 points; 7°) Argentina 22 points;	8°) Venezuela 22 points; 9°) Perú 15 points; 10°) Bolivia 14 points.

Fourth step

Following the third step, Argentina was could overtake reach Uruguay, considering that only one game outcome was left for allocation. Hence, the victory was conceded to Argentina over Uruguay. That way, the allocation of results from the last three competition days was completed without implementing the fifth step in the method.

As can be seen in the updated positions, Uruguay was in second position with the same score as Chile and Paraguay (Table 5). This indicated that with only three games to the end, there were still mathematical probabilities of qualifying for the World Cup, without checking the goal difference.

Table 5.  - Results allocated in the fourth step and updated standings 

Game No 16	Game No 17	Game No 18
Argentina defeats Paraguay	--	--
Updated standings after the fourth step: 1°) Brazil 39 points; 2°) Uruguay 27 points; 3°) Chile 27 points; 4°) Paraguay 27 points;	5°) Colombia 26 points; 6°) Argentina 25 points; 5°) Ecuador 24 points;	8°) Venezuela 22 points; 9°) Perú 15 points; 10°) Bolivia 14 points.

The rest is known history. Against all odds, Uruguay qualified for the FIFA World Cup in South Africa, after ending in the fifth position during the qualifiers, and winning the shared quota for the cup in the first and second leg matches against Costa Rica. In the World Cup, Uruguay showed its best performance in forty years, ranking fourth.

Results and discussion

Following is a discussion of the applicability, efficiency, rigorousness, and flexibility of the method suggested.

Applicability

So far, this method has been presented as a way of determining if a national selection has chances of qualifying for the FIFA World Cup. However, the application setting is much wider. In the first place, it can be used in several different soccer tournaments, as well as in other sports, even together with different scoring systems by game victory. Secondly, it can be applied regardless of how advanced the competition is. Lastly, it permits the utilization of several objectives, from being the champion to qualifying within the quota established for the first positions in a tournament.

In more general terms, the method is useful to determine if a contender in an ongoing competition comprising several matches, each of which adding points, can end the tournament within the first positions expected to fill the qualifying quota, considering the score achieved until then, and the games still to be played.

Efficiency and rigorousness

The question can also be answered correctly by analyzing all the possible result combinations, and designing the several different resulting positions. Nevertheless, it can be costly in terms of time and calculations.

Notwithstanding, the method provides an efficient solution since it minimizes the combinations to be analyzed with no loss of rigorousness. Accordingly, the results from pending matches are allocated, provided that with them, U will have a better final position, rather than using the alternative results.

Flexibility

One of the downsides of the method is the lack of realism, since the results are allocated without considering the likelihood of occurrence. However, this procedure derived from a question that needed to be answered. An event unlikely to take place does not mean it is mathematically unlikely; the history of soccer is rich in terms of unexpected results and epic victories ^{(Cattani, 2015, 226-227}; ^{Haberkorn, 2004, 21-32)}. Overcoming important challenges is within the essence of any sport.

Trying not to disrupt the above ideas, the method can also be used in a more flexible way to consider this aspect. In fact, several results thought to be highly probable can be allocated, because one of the national selections to play is already eliminated and has no major incentives to fight for a victory, as there are marked differences between them according to any objective indicator ^{(FIFA, 2018)}, or simply based on judgement. Then the method can be applied in relation to the remaining scheduled games. Naturally, in this case, a question different from the original would be answered.

The method can also be slightly adjusted to know if U can qualify for the World Cup just relying on the score achieved, without a better goal balance than their opponents. Accordingly, the first step will consist uniquely in granting the victories to U, whereas the third and fourth steps will only give the victories to the countries that cannot reach U scoring.

Finally, a similar method to the one suggested in this paper used to ensure development and rationale allows specialists to determine if a U country in the qualifiers is already qualified for the World Cup. In that direction, the results that lead to the worst possible ranking of U in the final positions should be given to the remaining games, then an evaluation must follow to determine if the country is out of the qualifying zone. The steps consist in allocating the following results: first the defeats to U by such a goal difference that it is in a disadvantageous position to any rival; second, granting the results of defeats to countries in the same position of overtaking U in the updated standings; third, giving the results of defeats to countries that cannot reach U in the standings. Finally, the games pending allocation need analysis of all the possible result combinations.

Conclusions

The people linked to sports, fans, players, coaches, or reporters, often want to know if a particular team or national selection holds a chance of meeting certain goals in the competition in progress, either being the champion or classifying for the next level. The method suggested in this article offers an efficient and rigorous way of responding this question. The efficiency of the method lies in that it permits the analysis of a minimum of possible result combinations, and it is mathematically rigorous, since it only discards irrelevant result combinations to provide the right responses.

Referencias bibliográficas

Alabarces, P., Amaral, W., Arrighi, P., Caetano, G., Delgado, G., Díaz, S., Fernández, F., González, A., Martínez, R., Morales, A., Piñeyrúa, R., Rodríguez, M., Vélez, B. y Yeghyaian, N. (2018). Uruguay en los mundiales. La búsqueda de la continuidad. Montevideo, Uruguay: Editorial Planeta. https://www.planetadelibros.com.uy/libro-uruguay-en-los-mundiales/273593

Asociación Uruguaya de Fútbol (2015). Eliminatoria Mundial Sudáfrica 2010. Asociación Uruguaya de Fútbol. https://www.auf.org.uy/eliminatoria-mundial-sud-aacute-frica-2010/

Bassorelli, G. (2014). El código celeste. Historias íntimas, anécdotas y polémicas de Uruguay en los mundiales. Montevideo, Uruguay: Ediciones de la Plaza. Pp. 422. ISBN/ISSN/DL: 978-9974-48-236-4, https://pmb.parlamento.gub.uy/pmb/opac_css/index.php?lvl=notice_display&id=83513

Castillo, F. y Varoli, H. (2013). Hasta la última gota. Vida de Fabián O’Neill. Montevideo, Uruguay: Editorial Sudamericana. https://books.google.com.cu/books/about/Hasta_la_%C3%BAltima_gota.html?id=CjUqnwEACAAJ&redir_esc=y

Cattani, R. (2015). El fútbol que más quiero. Salto, Uruguay: Sagitario Impresos.

Chiang, A.C. (1996). Métodos fundamentales de economía matemática. Tercera Edición. Madrid, España: McGraw-Hill. https://elvisjgblog.files.wordpress.com/2018/02/mc3a9todos-fundamentales-de-economc3ada-matemc3a1tica-4ta-edicic3b3n-alpha-c-chiang-freelibros-org.pdf

FBREF. (2010a). Estadísticas 2010 WCQ - CONMEBOL (M) FBref.https://fbref.com/es/comps/4/22/Estadisticas-2010-WCQ----CONMEBOL-M

FBREF. (2010b). Marcadores y partidos de 2010 WCQ CONMEBOL (M). FBref. https://fbref.com/es/comps/4/22/horario/Marcadores-y-partidos-de-2010-WCQ----CONMEBOL-M

FIFA. (2021.). FIFA World Cup Qatar 2022. FIFA. https://www.fifa.com/tournaments/mens/worldcup/qatar2022/qualifiers

FIFA. (2018). Revisión de la Clasificación Mundial FIFA/Coca-Cola. FIFA. https://www.fifa.com/es/fifa-world-ranking/procedure-men

Galeano, E. (1995). El fútbol a sol y a sombra. Montevideo, Uruguay: Ediciones del Chanchito. https://books.google.com.cu/books/about/El_f%C3%BAtbol_a_sol_y_sombra.html?id=Vy4oDwAAQBAJ&printsec=frontcover&source=kp_read_button&hl=es-419&redir_esc=y#v=onepage&q&f=false

Haberkorn, L. (2004). 9 historias uruguayas. Montevideo, Uruguay: Ediciones de la Plaza . http://www.rettalibros.com/shop/catalogs/show_material_details/23700

Kalnin, R.A. (1973). Álgebra y funciones elementales. Moscú, URSS: Editorial Mir. https://es.scribd.com/document/258441461/Algebra-y-Funciones-Elementales-R-Kalnin

Lissardy, A. L. (2011). Vamos que vamos. Un equipo, un país. Montevideo, Uruguay: Ediciones Santillana. https://fundaciongabo.org/es/vamos-que-vamos-un-equipo-un-pais

Piñón, E. (2009). La realidad pega fuerte. Diario El País, Año XCI, N° 31640, Sección Ovación, 4.

Rivas, E., y Señorans, J. (2003). Juan Ramón Carrasco. Un tipo auténtico. Montevideo, Uruguay: Ediciones de la Plaza. http://www.rettalibros.com/shop/catalogs/show_material_details/19116

Savia, J. (2009). Sueño congelado. Diario El País, Año XCI, N° 31640, Sección Ovación, 2.

Señorans, J. (2009). Perú, el verdugo. Diario El Observador, Año XVIII, N° 6016, Suplemento Al Toque, 2.

Woods, F. S., & Bailey, F. H. (1944). Analytic geometry and calculus. Boston, USA: The Athenaeum Press. https://books.google.com.cu/books/about/Calculus_with_Analytic_Geometry.html?id=oEucAQAACAAJ&redir_esc=y

Received: September 29, 2021; Accepted: October 13, 2021

^*Autor para la correspondencia: [e-mail]

El autor declara no poseer conflicto de intereses respecto a este texto.

Los autores han participado en la redacción del trabajo y análisis de los documentos.