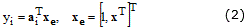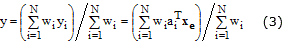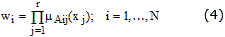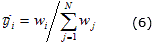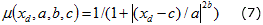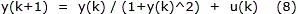ORIGINAL ARTICLE

 

 

A global fuzzy model for non linear systems using interval valued fuzzy sets

 

Un modelo difuso global para sistemas no lineales usando conjuntos difusos de intervalo evaluado

 

 

Francisco Herrera Fernández ^I, Etienne E. Kerre ^II, Boris L. Martínez Jiménez ^III 

^I Universidad Central "Marta Abreu" de Las Villas, Cuba.
^II University of Gent, Belgium.
^III Universidad Católica de Temuco, Chile.

 

 

---

ABSTRACT

This paper investigates the behavior of the fuzzy set in the antecedents of the Takagi Sugeno fuzzy model in identification of non linear and time variant systems. Data-driven techniques are applied by considering that measurement data are available. The principal question to solve in this paper is related with the representation of this kind of systems applying the concept of interval-valued fuzzy set. An overall model includes explicitly the nonlinear or time variant behavior of the system being identified by means of this concept using Takagi Sugeno fuzzy models. The determination of the nonlinear parameters of the antecedents is a central point in this modeling for time variant and nonlinear systems, because of the characteristics of these parameters. An illustrative experiment on a hybrid-tank system is conducted to present the benefits of the proposed approach.

Key words: Interval-valued fuzzy set, fuzzy identification, Takagi-Sugeno fuzzy model

RESUMEN

En este trabajo se investiga el comportamiento de los conjuntos difusos en los antecedentes de un modelo difuso del tipo Takagi Sugeno en la identificación de sistemas no linelaes y variantes en el tiempo. Técnicas de manejo de datos son aplicadas considerando que las mediciones están disponibles. EL principal problema a resolver en el trabajo está relacionado con la representación de este tipo de sistemas aplicando el concepto de conjunto difuso de intervalo evaluado. Un modelo general incluye de forma explícita el comportamiento no lineal o variante en el tiempo del sistema siendo identificado por medio de este concepto usando modelos difusos del tipo Takagi Sugeno. La determinación de ls parámetros no lineales de los antecedentes es aspecto esencial en esta modelación para sistemas variantes en el tiempo y no lineales debido a las características de estos parámetros. Un experimento ilustrativo de un sistema de tanque híbrido es realizado con el objetivo de presentar el enfoque propuesto.

Palabras Claves: Conjunto difuso de intervalo evaluado, identificación difusa, modelo difuso Takagi Sugeno

---

 

 

1.- INTRODUCTION

 

Many real-world problems are non-linear processes that require to be represented by adapting nonlinear models capable of representing the process dynamics. Particularly for nonlinear dynamic systems, the conventional techniques of modeling and identification are difficult to implement and sometimes impracticable. Therefore, there are demand for effective approaches to design self-developing systems which at the same time should be flexible and robust. Recently, several algorithms for on-line learning with self-constructing structure have been reported by including  techniques based on fuzzy logic  used for modeling this kind of processes [1- 14]. Specially the Takagi-Sugeno  model (TS) [15] has  been  extensively used. This model consists of if-then rules with fuzzy antecedents and mathematical functions in the consequent part. The task of system identification is to determine both the non-linear parameters of the antecedents and the linear parameters of the rules consequent.

During the past few years, significant attention has been given to data-driven techniques for generation of fuzzy models. It is well known that fuzzy systems are universal approximators, i.e., they can approximate any nonlinear continuous function to any prescribed accuracy if sufficient fuzzy rules are provided. The Takagi-Sugeno fuzzy model has become a powerful practical engineering tool for complex systems modeling because its capability of describing a highly nonlinear system using a small number of rules. Also fuzzy modeling involves structure and parameter identification.

The determination of the nonlinear parameters of the antecedent is a central point in this modeling for time variant and nonlinear systems, because of the characteristics of these parameters. Generally this situation is solved using linearization. Some methods based on data clustering are used for the structure identification. Clustering algorithms can be divided into two classes, off-line and on-line. Although a great number of clustering algorithms have been proposed, the majority of them process the data off-line, hence, the variant structure is ignored [10]. On-line clustering algorithms should be adaptive in the sense that up-to-date clusters are offered at any time, taking new data items into consideration as soon as they arrive. For continuous on-line learning of the TS fuzzy model, some on-line clustering methods responsible for the model structure (rule base) learning have been developed. [12, 16,17,18].

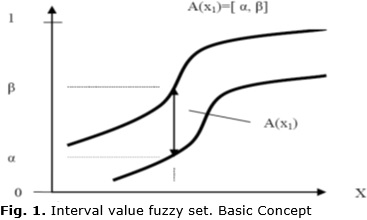
Another method besides clustering to obtain a global model is to consider the changing parameters in the antecedents. These parameters are changing continually. For that reason it is very important to obtain a correct determination of the membership function corresponding to the fuzzy sets in the antecedents. These fuzzy sets don't take unique values. In this sense a formal representation of this model implies use another concept. An alternative for these classes of systems are the interval-valued fuzzy sets, where the membership degrees are closed subintervals of [0,1], see Fig. 1.

In this form it's possible to determine a fuzzy set which can represent all regions in the space state visited for the operation point of the non linear and time variant process. The question is how to determine the parameters of these fuzzy sets and what relations exist between these parameters and the process parameters characterizing non linearity and time variability.

In this paper, a short application is developed in the identification of a non-linear system to explore the way to determine the global fuzzy set. Specially to determine the range where the antecedent fuzzy set can take values. These features make the approach potentially useful in adaptive control, robotics, diagnostic systems and as a tool for knowledge acquisition from data [12].

The rest of the paper is organized as follows. Section 2 gives a description of the TS fuzzy modeling. Section 3 gives a short explication of the algorithm for equation solving and simulation.  Section 4 presents the simulation results and Section 5 draws the concluding remarks. 

 

2.-TAKAGI-SUGENO FUZZY MODELING

 

The aim of this section is to describe a computationally efficient and accurate algorithm for on-line Takagi–Sugeno (TS) fuzzy model generation.

Our on-line dynamic fuzzy system uses the well-known Takagi–Sugeno inference engine [15]. Such fuzzy system is composed of N fuzzy rules indicated as follows:

Where x_j, j = 1,…, r, are input variables defined over universes of discourse X., and A_ij, are fuzzy sets defined by their fuzzy membership functions

µ_Aij: X_j → [0, 1].

Considering A_ij as interval-valued fuzzy set then

µ_Aij: X_j → I([0, 1])

where I ([0, 1]) denotes the class of all closed subintervals of [0, 1].  In the consequent parts, y_i is the rule output and a_ij are scalars.

For an input vector x = [x₁, x₂,…,x_r]^T, each of the consequent functions can be expressed as follows:

The result of inference, the output of the system y, is the weighted average of each rule output y_i, computed as follows:

The quantity w_i is the firing strength of the rule i. Equation (3) can be rewritten in the form:

where τ_i represents the normalized firing strength of the i-th rule. TS fuzzy rule-based model, as a set of local models, enables application of a linear LS method since this algorithm requires a model that is linear in the parameters.

Finally, all fuzzy membership functions are inverted bell-shape type functions because, in practice, partitions of this type are recommended when Tagaki-Sugeno consequents are used [18]. Inverted bell membership functions depend on three parameters as given by the following expression:

where:

c is the center of the bell (maximum value) on the x_d dimension,

a is the width of the inverted bell, and

b is proportional to the support of the fuzzy set.

If interval-valued fuzzy sets are used the result of inference changes. One needs to solve the expressions (3) and (4) where the operations multiplication and division must be solve with intervals and not with fixed numbers. 

 

3.-STRUCTURE IDENTIFICATION AND PARAMETERS DETERMINATION

 

The on-line learning algorithm consists of two main parts: structure identification and parameters determination. The object of structure identification is to select fuzzy rules by input-output clustering. In on-line identification, there is always new data coming, and the parameters should be updated according to the new data.

The first step is determine the numbers of input and rules. After that the linear functions in the consequent parts are created and updated using a linear least squares estimator. In this application the well-known method ANFIS was used.

The recursive procedure for on-line learning of TS models used in this paper, includes the following stages.

1) Stage 1: Initialization of the fuzzy model. For this:

          (a) Take the first m data samples from the data set.

          (b) Determine the input variables using initial fuzzy inference systems

          (c) Create the fuzzy model to be trained

2) Stage 2: At the next time step reading of the next data sample.

3) Stage 3: Recursive up-date of the model 

5) Stage 5: Up-grade of the antecedent parameters

6) Stage 6: Calculation of the consequent parameters

7) Stage 7: Prediction of the output for the next time step by the TS fuzzy model.

The execution of the algorithm continues for the next time step from stage 2. Stages 3 to 6 are solved using ANFIS technique.

 

4.- EXPERIMENTAL RESULTS

 

This analysis is realized on a hypothetical non-linear affine system, single input and single output, SISO, described by

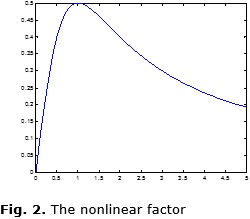
Fig. 2 shows the static characteristic of the non linearity, where it's possible to observe the change in the behavior around y(k) = 1.

Logically the behavior of output y depends on the operation point, that means in which zone or range is the input u. It will be analyzed the behavior in the following 3 zones or ranges for u:

Zone 1 Input and output/     u   random in [-5.5  -4.5]

Zone 2 Input and output/     u   random in [-0.5  +0.5]

Zone 3 Input and output/     u   random in [+4.5  +5.5]

 

The rules obtained are presented as:

If y(k-1) is A₁₁ and y(k-2) is A₂₁ and u(k-1) is A₃₁  then y(k) = p₁₀ + p₁₁y(k-1) + p₁₂y(k-2) + p₁₃u(k-1)

If y(k-1) is A₁₁ and y(k-2) is A₂₁ and u(k-1) is A₃₂  then y(k) = p₂₀ + p₂₁y(k-1) + p₂₂y(k-2) + p₂₃u(k-1)

If y(k-1) is A₁₁ and y(k-2) is A₂₂ and u(k-1) is A₃₁  then y(k) = p₃₀ + p₃₁y(k-1) + p₃₂y(k-2) + p₃₃u(k-1)

If y(k-1) is A₁₁ and y(k-2) is A₂₂ and u(k-1) is A₃₂  then y(k) = p₄₀ + p₄₁y(k-1) + p₄₂y(k-2) + p₄₃u(k-1)

If y(k-1) is A₁₂ and y(k-2) is A₂₁ and u(k-1) is A₃₁  then y(k) = p₅₀ + p₅₁y(k-1) + p₅₂y(k-2) + p₅₃u(k-1)

If y(k-1) is A₁₂ and y(k-2) is A₂₁ and u(k-1) is A₃₂  then y(k) = p₆₀ + p₆₁y(k-1) + p₆₂y(k-2) + p₆₃u(k-1)

If y(k-1) is A₁₂ and y(k-2) is A₂₂ and u(k-1) is A₃₁  then y(k) = p₇₀ + p₇₁y(k-1) + p₇₂y(k-2) + p₇₃u(k-1)

If y(k-1) is A₁₂ and y(k-2) is A₂₂ and u(k-1) is A₃₂  then y(k) = p₈₀ + p₈₁y(k-1) + p₈₂y(k-2) + p₈₃u(k-1)

Applying the algorithm described above for the three input zone the obtained antecedent parameters are:

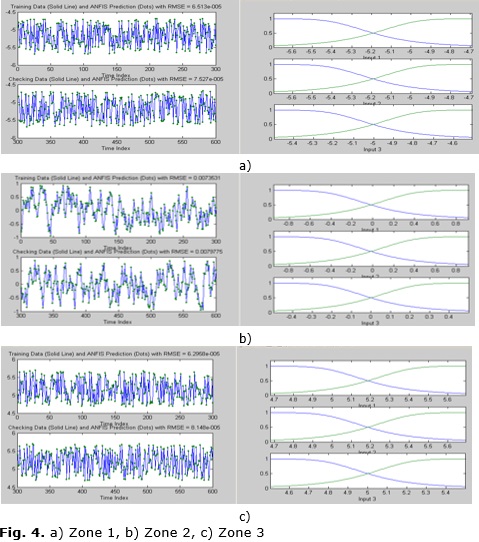
The results of the training and the final membership function for antecedents are shown in figures 4a), 4b) and 4c). These plots display error curves for both training and checking data. Logically the training error is higher than the checking error.  

But very important is the fact that for zone 2 both error are bigger than the error for the other two zones. The explication is in the accentuated non-linearity in this zone 2.

Taking only the first fuzzy set, A₁₁, as example it's possible to observe the variations in the value for this membership function. The fig. 5a shows how it's shifting with the zone, and fig. 5b) shows how the basic parameters of this fuzzy set also are different.

Fig. 5b) explains the possibility of applying the interval-valued fuzzy set concept for the description of nonlinear (and time variant) systems.

 

4.- CONCLUSIONS

 

This paper presented an approach for Takagi–Sugeno fuzzy model generation for a non-linear system, demonstrating the possibility of using interval-valued fuzzy set to represent this kind of systems.

Quantitative analysis demonstrates the possibility to solve this problem without using clustering algorithms. In this paper only non linear SISO systems were analyzed, but this principle can also be applied to time variant and MIMO systems.

The experiments show that as the parameters of the antecedent fuzzy set change, so it is possible to analyze the relation between these changes and the changes in the process parameters. This constitutes important further directions for research in this area

 

ACKNOWLEDMENTS

 

This paper is based on work supported in part by ended VLIR-UCLV Project: "Strengthening research and  postgraduated education in Computer Science".

 

REFERENCES

 

1. Hongmei J. Lianhua W. Interval-valued fuzzy subsemigroups and subgroups associated by intervalvalued Fuzzy graphs. In: WRI Global Congress on Intelligent Systems. Xiamen(China): 2009. p. 484-487.
2. Bustince H. Interval-valued Fuzzy Sets in Soft Computing. International Journal of Computational Intelligence Systems. 2010; 3(2): 215-222.
3. Bustince H, Montero J, Pagola M, Barrenechea E, Gomez D. A survey of interval-valued fuzzy sets. In: Pedrycz W, editors. Handbook of Granular Computing. New Jersey: Wiley; 2008. p. 489-515
4. Wang, CH, Cheng CS, Lee TT. Dynamical optimal training for interval type-2 fuzzy neural network (T2FNN). IEEE Transactions on Systems Man and Cybernetics: Part B, 2004; 34 (3): 1462-1477
5. Chen SH, Wang HY.Evaluating students answer scripts based on interval-valued fuzzy grade sheets. Expert Systems with Applications. 2009; 36 (6): 9839-9846
6. Sanz J, Fernandez A, Bustince F, Herrera F. A First Study on the Use of Interval-Valued Fuzzy Sets with Genetic Tuning for Classification with Imbalanced Data-Sets. In: 4th International Workshop on Hybrid Artificial Intelligence Systems. Salamanca(Spain): Springer Berlin Heidelberg; 2009. p. 581-588
7. Broumi S, Smarandach F. New Operations over Interval Valued Intuitionistic Hesitant Fuzzy Set. Mathematics and Statistics. 2014 2(2): 62-71
8. Xu ZS, Xia MM. On distance and correlation measures of hesitant fuzzy information. International Journal of Intelligent Systems. 2011; 26(5): 410-425
9. Kasabov NK, Song Q. DENFIS: Dynamic Evolving Neural-Fuzzy Inference System and its application for time-series prediction. IEEE Transactions on Fuzzy Systems. 2012; 10(2): 144-154
10. Li Z, Er MJ. A nonlinear transversal fuzzy filter with online clustering. In: 5th Asian Control Conference. Melbourne(Australia): 2004. p. 1585- 1593
11. Kukolj D, Levi E. Identification of complex systems based on neural and Takagi-Sugeno fuzzy model. IEEE Transactions on Systems, Man, and Cybernetics - Part B: Cybernetics. 2004; 34(1): 272-282
12. Angelov PP, Filev DP. An approach to online identification of Takagi-Sugeno fuzzy models. IEEE Transactions on Systems, Man, and Cybernetics - Part B: Cybernetics. 2004; 34(1): 484-498
13. Yu W, Ferreyra A. On-line clustering for nonlinear system identification using fuzzy neural networks. In: IEEE International Conference on Fuzzy Systems. Reno(USA): 2005. p. 678-683
14. Bouchachia A, Mittermeir R. Towards incremental fuzzy classifiers. Soft Computing - A Fusion of Foundations, Methodologies and Applications. 2007; 11(2): 193-207
15. Takagi T, Sugeno M. Fuzzy identification of systems and its applications to modeling and control. IEEE Transactions on Systems, Man, and Cybernetics. 1985; 15 (1): 116-132
16. Martínez B, Herrera F, Fernández, JA. Métodos de agrupamiento clásico para el modelado difuso en línea. In: Convención Internacional FIE'06. Santiago de Cuba(Cuba): 2006. p. 125-134
17. Martínez BL, Herrera F, Fernández JA, Marichal E. Método de Agrupamiento en Línea para la Identificación de Modelos Borrosos Takagi-Sugeno. Revista Iberoamericana de Automática e Informática Industrial. 2008; 5(3): 63-69

 

 

Received: 4 de february de 2016
Accepted: 2 de september de 2016

 

 

Francisco Herrera Fernández. Universidad Central "Marta Abreu" de Las Villas, Cuba. E-mail: [e-mail].