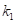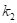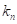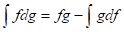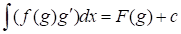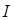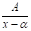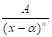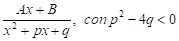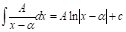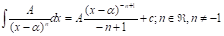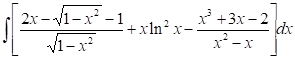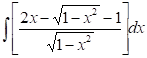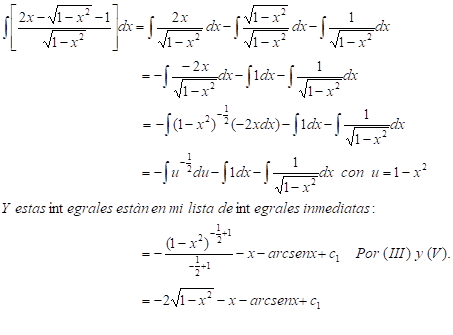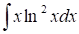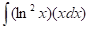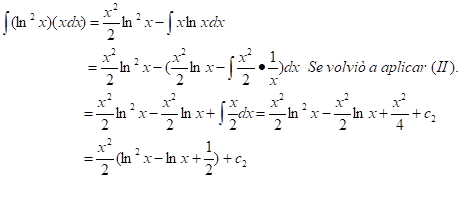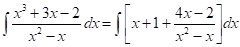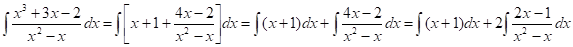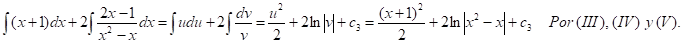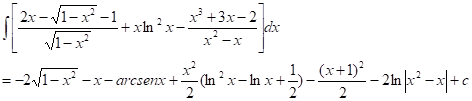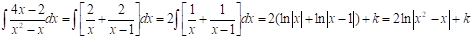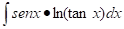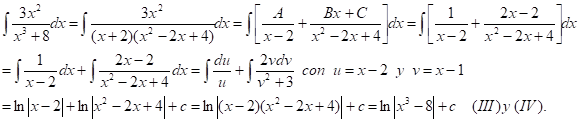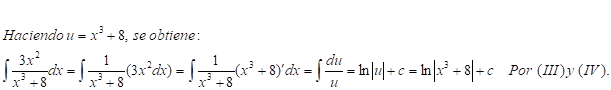Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Se concuerda con Cabrera, et al. (2011), al plantear que “la escuela, que en nuestra sociedad tiene entre sus tareas primordiales la de contribuir decisivamente a la formación multilateral de nuestros escolares, dedica gran parte de sus esfuerzos a crear las condiciones para que los alumnos aprendan a pensar”. (p.4). Alineada con tales esfuerzos está la inclusión de asignaturas de Matemática a lo largo de la enseñanza general y en la enseñanza superior, teniendo como base las potencialidades de la Matemática para contribuir al desarrollo del pensamiento lógico, elemento de vital importancia para la resolución de problemas en la vida escolar, la social y la laboral.
El uso de métodos heurísticos en las clases de Matemática propicia el rol activo de los estudiantes, realizando operaciones básicas del pensamiento tales como analizar, comparar, establecer analogías, generalizar, entre otras, contribuyendo por medio de estas a que ellos desarrollen la capacidad de resolver problemas, constituyendo esta, a decir de Ballester, et al. (2018), un elemento del aspecto instructivo de los objetivos de enseñanza aprendizaje de la Matemática.
En la enseñanza superior, una regularidad del proceso de enseñanza aprendizaje del Cálculo es la existencia de dificultades de los estudiantes en el cálculo manual de integrales indefinidas. Una de las principales causas de este fenómeno es la inexistencia de un procedimiento algorítmico para calcular cualquier integral indefinida, aun cuando el integrando es una función elemental dada mediante una fórmula sencilla, por lo que el cálculo de integrales indefinidas adquiere la connotación de problema, de ahí que cobre importancia la selección por el profesor(a) de métodos problémicos, fundamentado en su contribución a la reflexión, la actividad productiva de los estudiantes, el desarrollo del pensamiento creador y la independencia cognoscitiva.
Desarrollo
Con el objetivo de auxiliar a profesores en su actividad de enseñanza del cálculo de integrales indefinidas, se procederá a ejemplificar el uso de los métodos problémicos: de exposición problémica, el de conversación heurística y el de dirección del trabajo independiente, en medio de la resolución del problema de cálculo de integrales indefinidas.
Algunos conceptos y precisiones básicos (Rodríguez, et al., 1988; Jiménez, 2009; y Stewart, 2018).
Algunas fórmulas de integración básicas:
, donde 
, 
,…
son números reales.
Fórmula de integración por partes.
, siendo F una primitiva de f en 
(V)
En los casos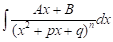
, donde 
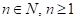, puede procederse a realizar la sustitución 
, con lo que se simplifica el cálculo de la integral.
A diferencia de la derivación , en la integración indefinida, no existen reglas generales para el cálculo de primitivas; no obstante, el análisis de la estructura del integrando y la práctica sistemática favorecerán la toma correcta de decisiones en torno a que técnica de integración usar en cada caso particular, si existen primitivas elementales. De lo que se trata es de tener disponibles nuestros recursos para descubrir cuál debe ser la clave de éxito.
Algunos recursos que pueden ser tenidos en cuenta son:
Las reglas de integración inmediata
Los métodos clásicos de integración: el de Sustitución y el de Integración por partes. En el caso de las funciones racionales fraccionarias: la división de polinomios y la descomposición de fracciones racionales propias en fracciones simples.
Las tablas de integrales.
Método de exposición problémica:
El docente expone el contenido mostrando la(s) vías de solución de un determinado problema. Diálogo mental entre profesor y estudiante; el primero se apoya en preguntas que él mismo responde (demuestra la lógica del razonamiento) para así guiar el pensamiento del estudiante (Colectivo de Autores, 2003).
Con la utilización de este método el profesor pretende familiarizar a los alumnos con la lógica contradictoria de la búsqueda de las soluciones de los problemas formulados en la clase. El profesor desarrolla en forma de diálogo mental el hilo conductor del razonamiento que lleva a la solución de los problemas originados por el planteamiento de situaciones problémicas (Ballester, et al., 2018).
Método de conversación heurística: En este método el profesor plantea a los estudiantes preguntas y tareas problémicas, cuya solución independiente se efectúa durante la conversación heurística (de búsqueda), los debates de los estudiantes y los comentarios a la realización independiente de experimentos. El descubrimiento de los nuevos hechos se produce como resultado del análisis de los datos de la tarea y de la generalización de los hechos presentados por el profesor. Lo que favorece a eliminar el formalismo, en la medida en que las situaciones que se le plantea a los estudiantes, activen su pensamiento, teniendo en cuenta el grado de dificultad en función del nivel de asimilación de los mismos (Cabrera, et al., 2011).
Se entiende por método de trabajo independiente aquel donde “el estudiante realiza tareas de manera independiente, bajo la guía del profesor”. (Colectivo de Autores, 2003, p.78)
Propuesta de metodología para calcular integrales indefinidas de funciones elementales, en términos de funciones elementales
Analizar el integrando de la integral, para decidir si esta forma parte de la lista de integrales declaradas como inmediatas:
Si se reconoce como inmediata, proceder a calcular la integral por medio de la tabla.
Si no se reconoce la integral como inmediata, valorar la posibilidad de transformarla en inmediata(s) aplicando operaciones aritméticas y/o identidades de alguno(s) de los tipos: algebraicas, trigonométricas, exponenciales y logarítmicas, o ensayar una sustitución. Si se intenta la sustitución, en principio, buscar una función presente en el integrando, además de su diferencial, quizá multiplicado por una constante. Si esto último se logra, se procede a declarar tal función como la variable auxiliar y proceder a aplicar la fórmula (III), y la (I) caso que el integrando quede expresado como una combinación lineal finita de funciones más fáciles de integrar.
Si las acciones anteriores resultaron infructíferas, proceder a clasificar el integrando en racional o no racional.
Si el integrando es una función racional expresada mediante una fracción de dos polinomios, clasificarla en propia o impropia :
Si la fracción es propia y, a la vez, una fracción simple (también se le dice parcial), aplicar la regla de integración correspondiente según el tipo de fracción simple.
Si es una fracción racional propia, pero no simple, proceder a descomponer en fracciones simples y luego continuar como en el inciso anterior; finalmente, hacer uso de (I).
Si la fracción racional es impropia, efectuar la división indicada, para obtener la suma de un polinomio y una fracción racional propia. En este caso, proceder a sumar la integral del polinomio y la de la fracción propia, de acuerdo con (I).
Si el integrando es una función no racional, valorar la posibilidad de aplicar alguna sustitución o el método de integración por partes, para obtener directamente el resultado o, al menos, reducir el integrando a uno que esté en alguna tabla de integrales.
Una vez calculada la integral, verificar si lo está o no correctamente procediendo a derivar el integrando.
Ejemplos de la aplicación de la metodología propuesta
Ejemplo 1(uso del método de exposición problémica)
Calcular la integral 
:
Quizá razonaría así:
No reconozco esta integral como una del grupo de integrales inmediatas; no obstante, el integrando es la suma de tres funciones. Pienso entonces en aplicar la fórmula (I), lo cual permite calcular, por separado, las tres integrales y luego sumarlas:
:
Una vez más, no reconozco la integral como inmediata, pero el integrando viene expresado en forma de cociente de una suma entre un monomio, por lo que, efectuando la división indicada y haciendo uso de la fórmula de integración (I), quizá logre expresar la integral por medio de una suma de integrales inmediatas o, al menos, más sencillas:
:
La integral no me resulta inmediata, tampoco se me ocurre ninguna transformación en el integrando, tampoco ninguna sustitución, al menos en principio. Pero el integrando es una función no racional y está en forma de producto, por lo que quizá sea útil la fórmula (II), de integración por partes. La elección que supongo conveniente es:
Hacemos entonces la elección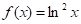
y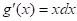 
, de donde resulta 
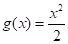y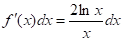 
. Entonces, al aplicar la fórmula (II), se obtiene:
La integral no me resulta inmediata, tampoco se me ocurre ninguna transformación en el integrando, tampoco ninguna sustitución, al menos en principio. Pero el integrando es una fracción racional impropia, por lo que se impone efectuar la división con resto, porque ello me conduciría a integrales de polinomios y de fracciones racionales propias, y sé cómo orientarme en tales casos:
Debido a que el integrando es una suma de funciones, aplicaré la fórmula (I) de integración:
Logrando las inmediatas:
Entonces
Notas:
Se pudo haber calculado la integral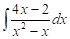
teniendo en cuenta que el integrando es una fracción racional propia no simple, por lo que se descompone en fracciones simples. Se tiene entonces que
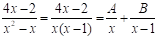y, al multiplicar la igualdad por el mcm de los denominadores, se obtiene 
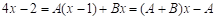, de donde resulta que 
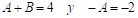, por lo que 
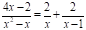y
Al verificar la corrección del cálculo la integral, si se recurre a un sistema algebraico computacional para derivar las primitivas encontradas, es posible que haya que realizar manipulaciones algebraicas para demostrar la equivalencia del integrando con la derivada mostrada por el sistema.
Ejemplo 2(uso del método de la conversación heurística)
Calcular la integral 
:
Pregunta formulada por el profesor(a): Guiándote por la metodología que se te brinda, ¿en torno a qué meditarías primero?
Respuesta que se espera emitan los estudiantes: En torno a si le reconozco alguna primitiva al integrando.
Pregunta formulada por el profesor(a): ¿Y reconoces alguna primitiva del integrando?
Respuesta que se espera emitan los estudiantes: No.
Pregunta formulada por el profesor(a): Entonces ¿qué propones?
Respuesta que se espera emitan los estudiantes: Tratar de transformar el integrando usando identidades, operaciones aritméticas o ambas cosas.
Preguntas formuladas por el profesor(a): ¿Para qué? ¿Cuál(es) en este caso?
Respuesta que se espera emitan los estudiantes: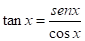 
.
Estímulo o impulso dado por el profesor(a) si no se logra la respuesta anterior: en general, ¿qué se ha hecho costumbre hacer cuando coexisten las razones trigonométricas seno, coseno y tangente?
Respuesta que se espera emitan los estudiantes: expresar la tangente en función del seno y el coseno:.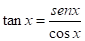
Pregunta formulada por el profesor(a): ¿Y qué obtienes si continúas por aquí?
Respuesta que se espera emitan los estudiantes: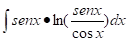 
Pregunta formulada por el profesor(a): ¿Consideras que has avanzado en encontrar la solución?
Respuesta que se espera emitan los estudiantes: No, esto no me resuelve.
Estímulo o impulso dado por el profesor(a): Consulta la metodología. ¿Qué se te recomienda?
Respuesta que se espera emitan los estudiantes: Bueno…el integrando no es racional…pero tiene forma de producto, por lo que pudiera pensar en la integración por parte.
Respuesta formulada por el profesor(a): Efectivamente, intentémoslo. De acuerdo con la estructura del producto, ¿cuál función propones para derivar?
Respuesta que se espera emitan los estudiantes: derivando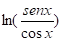
, tenemos: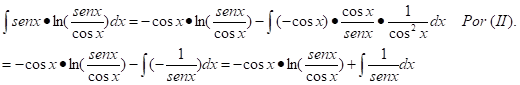
Y esta última integral se calcula inmediatamente con una tabla o un sistema algebraico computacional: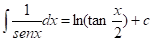
, por lo que la respuesta final es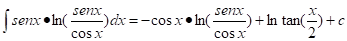
Ejemplo 3(uso del método de dirección del trabajo independiente)
Calcular la integral
:
Estímulos o impulsos dados por el profesor(a): ¿Le conoces alguna primitiva al integrando? Si tu respuesta es negativa, ten en cuenta que el integrando es una fracción racional propia no simple, porque el denominador es una suma de cubos, por lo que es de esperar que puedas factorizarlo completamente y proceder luego a la descomposición del integrando en fracciones simples: inténtalo.
Respuesta que emitieron (en medio de otros impulsos y correcciones) la mayoría los estudiantes durante la observación realizada por el profesor(a):
Respuesta emitida por el profesor(a): ¿Cómo saber si es correcta la respuesta?
Respuesta que emitieron los estudiantes: Derivando el resultado y chequear si se retorna a la función integrando.
Respuesta emitida por el profesor(a): Háganlo. ¿Este cálculo no les sugiere una vía más rápida para calcular la integral? ¿Cuál? Aplíquenla.
Respuesta que emitieron los estudiantes:
Conclusiones
El uso del método de exposición problémica, el de conversación heurística y el de dirección del trabajo independiente, durante la implementación de la metodología propuesta, propician la reactivación de conceptos y teoremas del cálculo integral que constituyen nivel de partida indispensable para el cálculo exitoso de integrales indefinidas.
Un correcto tratamiento didáctico del cálculo manual de este tipo de integrales contribuye al desarrollo del pensamiento lógico de los estudiantes, especialmente a través de su principal ámbito de manifestación: la resolución de problemas.
Disponer de tablas impresas de integrales indefinidas y las incorporadas en sistemas algebraicos computacionales no debe considerarse razón suficiente para prescindir definitivamente del cálculo manual de este tipo de integrales.
