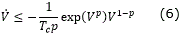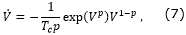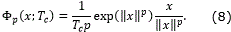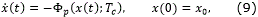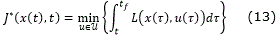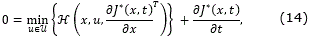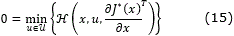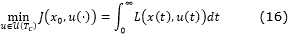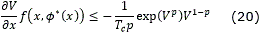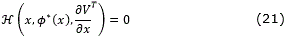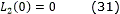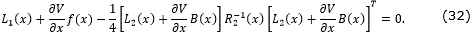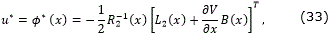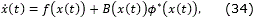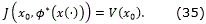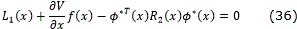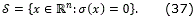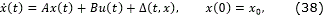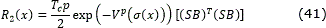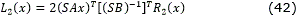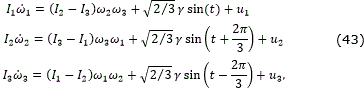Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Electrónica, Automática y Comunicaciones
versión On-line ISSN 1815-5928
EAC vol.38 no.1 La Habana ene.-abr. 2017
ORIGINAL ARTICLE
Optimal Predefined-Time Stabilization for a Class of Linear Systems
Estabilización de tiempo predefinido óptima para una clase de sistemas lineales
Esteban Jiménez-Rodríguez I, Juan Diego Sánchez-Torres II, Alexander G. Loukianov I
I Advanced Studies and Research Center of the National Polytechnic Institute (CINVESTAV). Guadalajara, México.
II Department of Mathematics and Physics of ITESO University. Guadalajara, México.
ABSTRACT
This paper addresses the problem of optimal predefined-time stability. Predefined-time stable systems are a class of fixed-time stable dynamical systems for which a bound of the settling-time function can be defined a priori as an explicit parameter of the system. Sufficient conditions for a controller to solve the optimal predefined-time stabilization problem for a given nonlinear system are provided. Furthermore, for nonlinear affine systems and a specific performance index, a family of inverse optimal predefined-time stabilizing controllers is derived. This class of controllers is applied to the inverse predefined-time optimization of the sliding manifold reaching phase in linear systems, jointly with the idea of integral sliding mode control to ensure robustness. Finally, as a study case, the developed methods are applied to an uncertain satellite system, and numerical simulations are carried out to show their behavior.
Key words: Hamilton-Jacobi-Bellman Equation, Lyapunov Functions, Optimal Control, Predefined-Time Stability.
RESUMEN
Este trabajo trata el problema de estabilidad óptima en tiempo predefinido. Los sistemas estables en tiempo predefinido son una clase de sistemas que presentan la propiedad de estabilidad en tiempo fijo y, además, una cota de la función de tiempo de convergencia puede ser definida a priori como un parámetro explícito del sistema. En el trabajo se proporcionan condiciones suficientes para que el problema de estabilización optima en tiempo predefinido sea soluble dado un sistema no lineal. Además, para sistemas no lineales afines al control y un índice de desempeño específico, se deriva una familia de controladores estabilizantes en tiempo predefinido. Esta clase de controladores se aplica a la optimización inversa en tiempo predefinido de la fase de alcance de variedades deslizantes en sistemas lineales, junto con la idea de modos deslizantes integrales para brindar robustez. Finalmente, como caso de estudio, los métodos desarrollados se aplican a un sistema de satélite con incertidumbre, y se llevan a cabo simulaciones numéricas para validar su comportamiento.
Palabras Claves: Ecuación de Hamilton-Jacobi-Bellman, Funciones de Lyapunov, Control Óptimo, Estabilidad de tiempo predefinido
1.- INTRODUCTION
Finite-time stable dynamical systems provide solutions to applications which require hard time response constraints. Important works involving the definition and application of finite-time stability have been carried out in [1-5] Nevertheless, this finite stabilization time is often an unbounded function of the initial conditions of the system. Making this function bounded to ensure the settling time is less than a certain quantity for any initial condition may be convenient, for instance, for optimization and state estimation tasks. With this purpose, a stronger form of stability, in which the convergence time presents a class of uniformity with respect to the initial conditions, called fixed-time stability was introduced [6-9]. When fixed-time stable dynamical systems are applied to control or observation, it may be difficult to find a direct relationship between the gains of the system and the upper bound of the convergence time; thus, tuning the system in order to achieve a desired maximum stabilization time is not a trivial task.
In this sense, another class of dynamical systems which exhibit the property of predefined-time stability, have been studied [10,11]. For these systems, an upper bound of the convergence time appears explicitly in their dynamical equations; in particular, it equals the reciprocal of the system gain. Moreover, for unperturbed systems, this bound is not a conservative estimation but truly the minimum value that is greater than all the possible exact settling times.
On the other hand, the infinite-horizon, nonlinear non-quadratic optimal asymptotic stabilization problem was addressed in [12]. The main idea of the results are based on the condition that a Lyapunov function for the nonlinear system is at the same time the solution of the steady-state Hamilton-Jacobi-Bellman equation, guaranteeing both asymptotic stability and optimality. Nevertheless, returning to the first paragraph idea, the finite-time stability is a desired property in some applications, but optimal finite-time controllers obtained using the maximum principle do not generally yield feedback controllers. In this sense, the optimal finite-time stabilization is studied in [13], as an extension of [12]. Since the results are based on the framework developed in [12], the controllers obtained are feedback controllers.
Consequently, as an extension of the ideas presented in [11-14], this paper addresses the problem of optimal predefined-time stabilization, namely the problem of finding a state-feedback control that minimizes certain performance measure, guaranteeing at the same time predefined-time stability of the closed-loop system. In particular, sufficient conditions for a controller to solve the optimal predefined-time stabilization problem for a given system are provided. These conditions involve a Lyapunov function that satisfy both a certain differential inequality for guaranteeing predefined-time stability and the steady-state Hamilton-Jacobi-Bellman equation for ensuring optimality. Furthermore, this result is applied to the predefined-time optimization of the sliding manifold reaching phase in linear systems, jointly with the integral sliding mode control idea to provide robustness. Finally, as a study case, the predefined-time optimization of the sliding manifold reaching phase in an uncertain satellite system is performed using the developed methods, and numerical simulations are carried out to show their behavior.
2.- MATHEMATICAL PRELIMINARES: PREDEFINED-TIME STABILITY
Consider the system
where x ∈ ℜn is the system state, ρ ∈ ℜb stands for the system parameters and f:ℜn→ℜn is a function such that f(0)=0, i.e. the origin x=0 is an equilibrium point of (1).
Definition 1.1. [8] The origin of (1) is globally finite-time stable if it is globally asymptotically stable and any solution x(t,x0) of (1) reaches the equilibrium point at some finite time moment, i.e., ∀ t ≥ T(x0):x(t,x0)=0, where T: ℜn→ℜ+ ∪ {0}.
Remark 1.1. The settling-time function T(x0) for systems with a finite-time stable equilibrium point is usually an unbounded function of the system initial condition.
Definition 1.2. [8] The origin of the system (1) is fixed-time stable if it is globally finite-time stable and the settling-time function is bounded, i.e. ∃ Tmax > 0:∀ x0∈ ℜn: T(x0)≤ Tmax.
Remark 1.3. Note that there are several choices for Tmax. For instance, if the settling-time function is bounded by Tm, it is also bounded by λTm for all λ≥1. This motivates the following definition.
Definition 1.3. [11] Assume that the origin of the system (1) is fixed-time stable. Let Τ be the set of all the bounds of the settling-time function for the system (1), i.e.,
Then, the minimum bound of the settling-time function Tf, is defined as
Remark 1.2. The time Tf in the above definition can be considered as the true fixed-time in which the system (1) is stabilized.
Definition 1.4. [11] For the case of fixed-time stability when the system (1) parameters ρ can be expressed in terms of Tmax or Tf (a bound or the least upper bound of the settling-time function), it is said that the origin of the system (1) is predefined-time stable.
With the above definition, the following lemma provides a Lyapunov-like condition for predefined-time stability of the origin:
Lemma 1.1. [10] Assume there exist a continuous radially unbounded function V: ℜn→ℜ+ ∪ {0}, and real numbers Tc >0 and 0<p≤1, such that the system (1) parameters ρ can be expressed as a function of Tc >0, and
and the time derivative of V along the trajectories of the system (1) satisfies the differential inequality
Then, the origin of the system (1) is predefined-time stable with T(x0) ≤ Tc.
Remark 1.3. Lemma 1.1 characterizes fixed-time stability in a very practical way since the condition (6) directly involves a bound on the convergence time. However, this condition is not sufficient for Tc to be the least upper bound of the settling-time function T(x0). A sufficient condition is provided in the following corollary of Lemma 1.1.
Corollary 1.1. Under the same conditions of Lemma 1.1, if the time derivative of V along the trajectories of the system (1) satisfies differential equation
then, the origin of the system (1) is predefined -time stable with 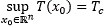 .
.
Remark 1.4. Note that the equality condition (7) is more restrictive than the inequality (6), in the sense that to obtain the equality in (7) no uncertainty in the system model is allowed.
Definition 1.5. [11] For x ∈ ℜn, 0<p≤1 and Tc >0, the predefined-time stabilizing function is defined as
Remark 1.5. The function Φp(x; Tc) is continuous and non-Lipschitz for 0<p<1, and discontinuous for p=1.
The following two lemmas give meaning to the name "predefined-time stabilizing function".
Lemma 1.2. [11] For every initial condition x0, the origin of the system
with Tc >0, and 0<p≤1 is predefined-time stable with 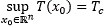 .
.
The previous results have been applied to design a robust predefined-time controller for the perturbed system
with x, u ∈ ℜn and Δ: ℜ+ × ℜn→ℜn. The objective is to drive the system (10) state to the point x=0 in a predefined time, in spite of the unknown perturbation Δ(t, x).
Lemma 1.3. [11] Let the function Δ(t ,x) be considered as an unknown non-vanishing perturbation bounded by |Δ(t, x)|≤δ, with 0<δ<∞. Then, selecting the control input as
with Tc >0, 0<p<1 and k≥δ, ensures the closed-loop system (10)-(11) origin is predefined-time stable with T(x0) ≤ Tc.
2.1.- MATHEMATICAL PRELIMINARES: OPTIMAL CONTROL THEORY
Consider the controlled nonlinear system
where x ∈ ℜn is the system state, u ∈ ℜm is the system control input, which is restricted to belong to a certain set U ⊂ ℜm of the admissible controls, and f:ℜn × ℜm → ℜn is a nonlinear function with f(0,0)=0.
The control objective is to design a control law for the system (12) such that the following performance measure J(x0,u(⋅))=∫0tf L(x(t), u(t))dt is minimized. Here, L: ℜn × ℜm → ℜ is a continuous function, assumed to be convex in u.
Define the minimum cost function J*(x(t), t) as
Then, defining the Hamiltonian, for p ∈ ℜn (usually called the costate), H(x,u,p)=L(x,u)+pT f(x,u), the Hamilton-Jacobi-Bellman (HJB) equation can be written as
that provides a sufficient condition for optimality.
For infinite-horizon problems (limit as tf→∞), the cost does not depend on t anymore and the partial differential equation (14) reduces to the steady-state HJB equation
which will be used in foregoing.
3.- OPTIMAL PREDEFINED-TIME STABILIZATION
Definition 3.1. Consider the optimal control problem for the system (12)
where U(Tc)={u(⋅):u(⋅) stabilizes (12) in a predefined time Tc}. This problem is called as the optimal predefined-time stabilization problem for the system (12).
The following theorem gives sufficient conditions for a controller to solve this problem.
Theorem 3.1. Assume there exist a C1 radially unbounded function V: ℜn → ℜ+ ∪ {0}, real numbers Tc >0 and 0<p< 1, and a control law ϕ*: ℜn → ℜm such that
Then, with the feedback control
the origin x=0 of the closed-loop system
is predefined-time stable with T(x0) ≤ Tc. Moreover, the feedback control law (23) minimizes J(x0, u(⋅)) (18) in the sense that
Proof. Applying Lemma 1.1 to the closed-loop system (24), predefined-time stability with predefined time Tc follows directly from the conditions (17)-(20).
To prove (25), let x(t) be a solution of the system (24). Then,
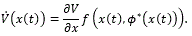
From the above and (21) it follows
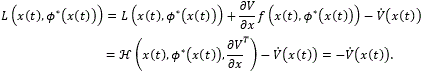
Hence,
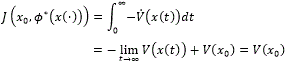
Now, let u(⋅) ∈ U(Tc) and let x(t) be the solution of (12), so that
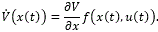
Then,
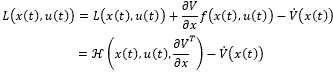
Since u(⋅) stabilizes (12) in predefined time Tc, using (21) and (22) we have
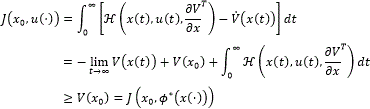
Remark 3.1. It is important that the optimal predefined-time stabilizing controller u*=ϕ*(x) characterized by Theorem 3.1 is a feedback controller.
Remark 3.2. Note that the conditions (17)-(22) involve a C1 predefined-time Lyapunov function (see Lemma 1.1) that is also a solution of the steady state Hamilton-Jacobi-Bellman equation (15). As usual in optimal control theory, these existence conditions are quite restrictive. However, these conditions are very useful to obtain an inverse optimal predefined-time stabilizing controller, for instance, for a class nonlinear affine control systems with relative degree one. This is a typical case in sliding mode control design, and it will be considered in foregoing.
To derive a closed-form expression for the controller, the result of Theorem 3.1 is specialized to nonlinear affine control systems of the form
where x ∈ ℜn is the system state, u ∈ ℜm is the system control input, f: ℜn → ℜn is a nonlinear function with f(0)=0 and B:ℜn → ℜn×m.
The performance integrand is also specialized to
where L1: ℜn → ℜ, L2: ℜn → ℜ1×m and R2: ℜn → ℜm×m is a positive definite matrix function.
Theorem 3.2. Assume there exist a C1 radially unbounded function V: ℜn → ℜ+ ∪ {0}, and real numbers Tc >0 and 0<p< 1 such that
Then, with the feedback control
the origin of the closed loop system
is predefined-time stable with T(x0) ≤ Tc. Moreover, the performance measure J(x0, u(⋅)) is minimized in the sense of (25) and
Proof. Under these conditions the hypotheses of Theorem 3.1 are satisfied. In fact, the control law (33) is obtained solving 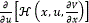 =0 with L(x, u) specialized to (27). Then, setting u*=ϕ*(x) as in (33), the conditions (28), (29) and (30) become the hypotheses (17), (18) and (20), respectively.
=0 with L(x, u) specialized to (27). Then, setting u*=ϕ*(x) as in (33), the conditions (28), (29) and (30) become the hypotheses (17), (18) and (20), respectively.
On the other hand, since the function V is C1, and by (28)-(29) V has a local minimum at the origin, then 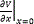 =0. Consequently, the hypothesis (19) follows from (31) and the fact that
=0. Consequently, the hypothesis (19) follows from (31) and the fact that 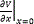 .
.
Since ϕ*(x) satisfies 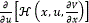 u=ϕ*(x)=0, and noticing that (23) can be rewritten in terms of ϕ*(x) as
u=ϕ*(x)=0, and noticing that (23) can be rewritten in terms of ϕ*(x) as
then the hypothesis (21) is directly verified.
Finally, from (21), (33) and the positive definiteness of R2(x) it follows
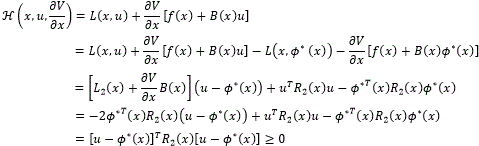
which is the hypothesis (22). Applying Theorem 3.1, the result is obtained.
Remark 3.4. The expression (33) provided by Theorem 3.2 can be used to construct an inverse optimal controller, in the following sense: instead of solving the steady-state HJB equation directly to minimize some given performance measure, one can flexibly specify L2(x) and R2(x), while from (36) L1(x) is parameterized as in (36).
Remark 3.5. As in Theorem 3.1, it is not always easy to satisfy the hypotheses (28)-(32) of Theorem 3.2. However, for affine systems with relative degree one, the functions L2(x) and R2(x) can be chosen such that the conditions (28)-(32) are fulfilled.
4.- INVERSE OPTIMAL PREDEFINED-TIME SLIDING MANIFOLD ReacHING IN LINEAR SYSTEMS.
Definition 4.1. [15] Let σ: ℜn → ℜm be a smooth function, and define the manifold
If for an initial condition x0 ∈ S, the solution of (1) x(t, x0) ∈ S for all t, the manifold S is called an integral manifold.
Definition 4.2. [15] If there is a nonempty set N ⊂ ℜn-S such that for every initial condition x0∈ N, there is a finite time ts >0 in which the state of the system (1) reaches the manifold S (39), then the manifold S is called a sliding mode manifold.
Consider the following linear time-invariant system subject to perturbation:
where x ∈ ℜn is the system state, u ∈ ℜm, with m≤n, is the system control input, Δ: ℜ+ × ℜn → ℜn is the system perturbation, A ∈ ℜn×n, and B ∈ ℜn×m has full rank.
Moreover, consider the function σ:ℜn → ℜm as a linear combination of the states
σ(x)=Sx
where S ∈ ℜm×n is full rank.
With the above definitions, the main objective of the controller is to optimally drive the trajectories of the system (38) to the set S={x ∈ ℜn: Sx=0} (7) in a predefined time in spite of the unknown perturbation Δ(t, x). The matrix S is selected so that the motion of the system (38) restricted to the sliding manifold σ(x)=Sx=0 has a desired behavior.
The dynamics of σ are described by
It is assumed that the matrix S is selected such that the square matrix SB ∈ ℜm×m is nonsingular, i.e., such that the system (39) has relative degree one. This can be easily accomplished since B is full rank.
Unperturbed case
Consider the case when Δ(t, x)=0. The following result gives an explicit form of the functions V, R2 and L2 which characterize the optimal predefined-time stabilizing feedback controller (33).
Corollary 4.1. Consider the system (39) in absence of the perturbation term, i.e., Δ(t, x)=0. The feedback controller (33) with the functions V, R2 and L2 selected as
with Tc>0, 0<p<1 and 4c=(p+1)2, stabilizes the system (39) in predefined time with sup T(σ0)=Tc. Moreover, this controller solves the optimal predefined-time stabilization problem (16) for the system (39) with the performance integrand L(x, u)=L1(x)+L2(x)u+uTR2(x)u, where L2 and R2 are given by (42) and (41), respectively, and L1 is given by (36).
Proof. It is easy to see that all the conditions of Theorem 3.2 are satisfied. Indeed, note that the function V in (40) is C1, and satisfies the hypotheses (28) and (29). In the same manner, the function L2 in (42) satisfies the hypothesis (31), and defining the function L1 as in (36), the hypothesis (32) is also satisfied.
On the other hand, the derivative of V along  =SAx+SBϕ* is calculated as (note that
=SAx+SBϕ* is calculated as (note that 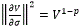 )
)
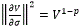
Thus, the hypothesis (30) is satisfied. Then, the result is obtained by direct application of Theorem 3.2.
Perturbed case
Now, consider the case when Δ(t, x) is a matched non-vanishing perturbation. Under the idea of integral sliding mode control [16-17], the following result provides a controller that rejects the perturbation term Δ(t, x) in predefined-time and, once the perturbation term is rejected, this controller optimally stabilizes the system (39) in predefined-time.
Corollary 4.2. Consider the system (39) and let the function Δ(t, x) be a matched and non-vanishing perturbation term, i.e. there exists a function 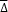 (t, x) such that Δ(t, x)=B
(t, x) such that Δ(t, x)=B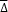 (t, x) and ‖
(t, x) and ‖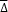 (t, x)‖≤δ, with 0<δ<∞ a known constant. Then, splitting the control function $u$ into two parts, u=u0+u1, and selecting
(t, x)‖≤δ, with 0<δ<∞ a known constant. Then, splitting the control function $u$ into two parts, u=u0+u1, and selecting
(i) u0 as the optimal predefined-time stabilizing feedback controller (33), with the functions V, R2 and L2 as in Corollary 4.1 with parameters Tc2>0 and 0<p2<1, and
(ii) u1=-(SB)-1 [k‖SB‖ s/‖s‖ + Φp1(s; Tc1))], with Tc1>0, 0<p1<1, k≥δ, and the auxiliary sliding variable s=σ+z, where z is an integral variable, solution of  =-SAx-SBu0,
=-SAx-SBu0,
the system perturbation term 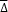 (t, x) is rejected in predefined time Tc1 and, once the perturbation term is rejected, the system (39) is optimally predefined-time stabilized with predefined time T(σ0) ≤Tc2, with respect to the performance L(x, u)=L1(x)+L2(x)u+uTR2(x)u, where L2 and R2 are given by (42) and (41), respectively, and L1 is given by (36).
(t, x) is rejected in predefined time Tc1 and, once the perturbation term is rejected, the system (39) is optimally predefined-time stabilized with predefined time T(σ0) ≤Tc2, with respect to the performance L(x, u)=L1(x)+L2(x)u+uTR2(x)u, where L2 and R2 are given by (42) and (41), respectively, and L1 is given by (36).
Proof. By the definition of s, σ, z and u1, the dynamics of s are obtained as
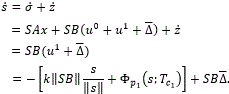
By direct application of Lemma 1.3, s=0 for t>Tc1. Once the dynamics of (39) are constrained to the manifold s=0, then, from s=0, the equivalent control (3) value of u1 is u1eq=-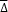 . Therefore, the sliding mode dynamics of σ,
. Therefore, the sliding mode dynamics of σ,  =SAx+SBu0, are invariant with respect to the perturbation. By the definition of u0 a direct application of Corollary 4.1 yields the desired result.
=SAx+SBu0, are invariant with respect to the perturbation. By the definition of u0 a direct application of Corollary 4.1 yields the desired result.
5.- EXAMPLE
Consider a satellite system as presented in [18], subject to external disturbances
where, for i=1,2,3; ωi are the angular velocities of the satellite around the principal axes, ui are the control input torques, and Ii represent the moments of inertia.
Defining xi=ωi for i=1,2,3; x=[x1 x2 x3]T, and u=[u1 u2 u3]T, the system (43) can be represented as the linear perturbed system
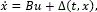
where Δ(t, x)=B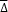 (t, x) is a matched perturbation which represents the nonlinearities and uncertainties, with B=diag(1/I1, 1/I2, 1/I3), and
(t, x) is a matched perturbation which represents the nonlinearities and uncertainties, with B=diag(1/I1, 1/I2, 1/I3), and 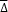 (t, x)=[(I2 - I3)x2x3+√(2⁄3)γ·sin(t)·(I3 - I1)x3x1 + √(2⁄3)γ·sin(t+2π/3)·(I1 - I2)x1x2 + √(2⁄3)γ·sin(t-2π/3)]T. Furthermore ‖
(t, x)=[(I2 - I3)x2x3+√(2⁄3)γ·sin(t)·(I3 - I1)x3x1 + √(2⁄3)γ·sin(t+2π/3)·(I1 - I2)x1x2 + √(2⁄3)γ·sin(t-2π/3)]T. Furthermore ‖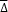 (x)‖≤δ+γ, with δ:=
(x)‖≤δ+γ, with δ:=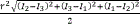 for ‖x‖≤r.
for ‖x‖≤r.
The goal is to optimally stabilize the equilibrium point x=0 of the satellite (eliminate rotation movements around the principal axes) in predefined time. With this aim, choose σ(x)=Sx, with S=diag(I1, I2, I3) so that SB=I3×3.
According to Corollary 4.2, u0 is implemented as in (33) with the functions V, R2 and L2 selected as
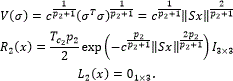
On the other hand, z and u1 are chosen according to the part (ii) of Corollary 4.2.
Simulations were conducted using the Euler integration method, with a fundamental step size of 1×10-4 s. The numerical values of the parameters are I1=1 kg⋅m2, I2=0.8 kg⋅m2, I3=0.4 kg⋅m2 and γ=0.5. The initial conditions of the integrators were selected as: x(0)=[0.5 -1 2]T, and z(0)=[0 0 0]T. In addition, the controller gains were adjusted to: Tc1=1, Tc2=1, k=3.9 p1=1/3 and p2=1/3.
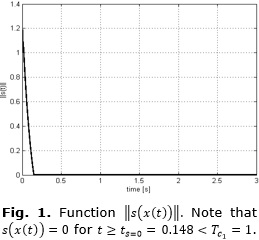
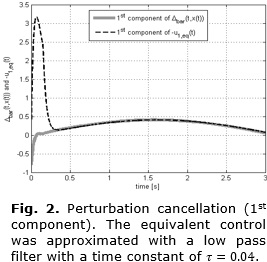
Note that s(t)=0 for t≥0.148s:=ts=0<Tc1=1s (see Figure 1), and from that instant on, the equivalent control signal u1eq (approximated using the low-pass filter 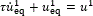 , with τ=0.04, see [3]) cancels the perturbation term
, with τ=0.04, see [3]) cancels the perturbation term 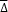 (t, x)=[(I2 - I3)x2x3+√(2⁄3)γ·sin(t)·(I3 - I1)x3x1 + √(2⁄3)γ·sin(t+2π/3)·(I1 - I2)x1x2 + √(2⁄3)γ·sin(t-2π/3)]T (see Figure 2).
(t, x)=[(I2 - I3)x2x3+√(2⁄3)γ·sin(t)·(I3 - I1)x3x1 + √(2⁄3)γ·sin(t+2π/3)·(I1 - I2)x1x2 + √(2⁄3)γ·sin(t-2π/3)]T (see Figure 2).
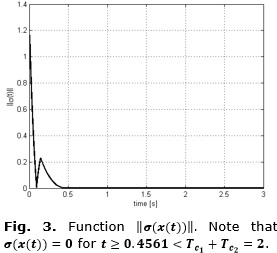
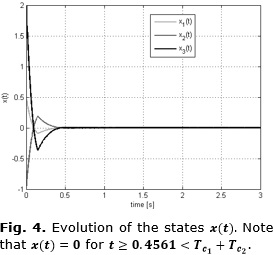
Once the perturbation is canceled, the optimal predefined-time stabilization of the variable σ(t) takes place. It can be seen that σ(t)=0 for t≥0.4561 s<Tc1+Tc2=2s (see Figure 3). It can be noticed that σ(x)=Sx=0, if and only if x=0 since S=diag(I1, I2, I3) is invertible. Then, for t≥0.4561s<Tc1+Tc2=2s, the state x(t)=0 (see Figure 4).
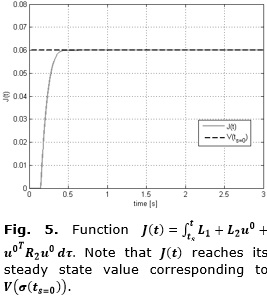
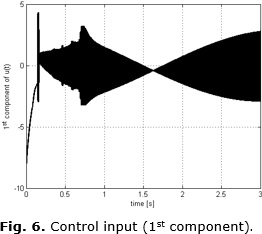
Figure 5 shows that the cost, as a function of time, grows quickly to a steady state value corresponding to $V(σ(ts=0)). Finally, Figure 6 shows the first component of the control signal (torque) versus time. It is important to remark that this controller yields discontinuous signals in order to cancel the persistent perturbation  (t, x).
(t, x).
6.- CONCLUSIONS
In this paper, the problem of optimal predefined-time stability was investigated. Sufficient conditions for a controller to be optimal predefined-time stabilizing for a given nonlinear system were provided. Moreover, under the idea of inverse optimal control, and considering nonlinear affine systems and a certain class of performance integrand, the explicit form of the controller was also derived. This class of controllers was applied to the predefined-time optimization of the sliding manifold reaching phase in linear systems, considering both the unperturbed and the perturbed cases. For the unperturbed case, the developed result was applied directly, while for the perturbed case it was used jointly with the idea of integral sliding mode control to provide robustness. The developed control schemes were performed for the predefined-time optimization of the sliding manifold reaching phase in a satellite system model. Simulation results supported the expected results.
REFERENCES
1. Roxin E. On finite stability in control systems. Rend del Circ Mat di Palermo. 1966;15(3):273–82.
2. Haimo V. Finite Time Controllers. SIAM J Control Optim. 1986;24(4):760–70.
3. Utkin VI. Sliding Modes in Control and Optimization. New York: Sciences; 1992. p. 286.
4. Bhat S, Bernstein D. Finite-Time Stability of Continuous Autonomous Systems. SIAM J Control Optim. 2000;38(3):751–66.
5. Moulay E, Perruquetti W. Finite-Time Stability and Stabilization: State of the Art. In: Edwards C, Fossas Colet E, Fridman L, editors. Advances in Variable Structure and Sliding Mode Control. Berlin: Springer Berlin Heidelberg; 2006. p. 23–41.
6. Andrieu V, Praly L, Astolfi A. Homogeneous Approximation, Recursive Observer Design, and Output Feedback. SIAM J Control Optim. 2008;47(4):1814–50.
7. Cruz-Zavala E, Moreno JA, Fridman L. Uniform Second-Order Sliding Mode Observer for mechanical systems. In: Proceedings of the 2010 11th International Workshop on Variable Structure Systems (VSS 2010). 2010. p. 14–9.
8. Polyakov A. Nonlinear Feedback Design for Fixed-Time Stabilization of Linear Control Systems. IEEE Trans Automat Contr. 2012;57(8):2106–10.
9. Polyakov A, Fridman L. Stability notions and {L}yapunov functions for sliding mode control systems. J Franklin Inst. 2014;351(4):1831–65.
10. Sánchez-Torres JD, Sánchez EN, Loukianov AG. A discontinuous recurrent neural network with predefined time convergence for solution of linear programming. In: IEEE Symposium on Swarm Intelligence (SIS). 2014. p. 9–12.
11. Sánchez-Torres JD, Sanchez EN, Loukianov AG. Predefined-time stability of dynamical systems with sliding modes. In: American Control Conference (ACC) 2015. 2015. p. 5842–6.
12. Bernstein DS. Nonquadratic Cost and Nonlinear Feedback Control. Int J Robust Nonlinear Control. 1993;3(1):211–29.
13. Haddad WM, L’Afflitto A. Finite-Time Stabilization and Optimal Feedback Control. IEEE Trans Automat Contr. 2016;61(4):1069–74.
14. Jiménez-Rodríguez E, Sánchez-Torres JD, Loukianov AG. On Optimal Predefined-Time Stabilization. In: Proceedings of the XVII Latin American Conference in Automatic Control. 2016. p. 317–22.
15. Drakunov S V., Utkin VI. Sliding mode control in dynamic systems. International Journal of Control. 1992; 55(4): 1029–37.
16. Matthews GP, DeCarlo RA. Decentralized tracking for a class of interconnected nonlinear systems using variable structure control. Automatica. 1988;24(2):187–93.
17. Utkin VI, Shi J. Integral sliding mode in systems operating under uncertainty conditions. In: Proc 35th IEEE Conf Decis Control. 1996. p. 4.
18. Shtessel Y, Edwards C, Fridman L, Levant A. Sliding Mode Control and Observation. New York: Springer; 2014.
Received: 15 de septiembre del 2016
Approved: 8 de enero del 2017
Esteban Jiménez Rodríguez, Advanced Studies and Research Center of the National Polytechnic Institute -CINVESTAV-, Campus Guadalajara, México. E-mail: esjimenezro@gmail.com.