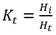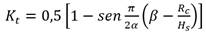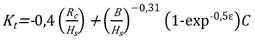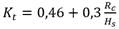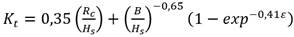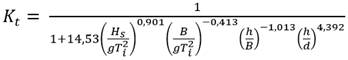Introducción
México cuenta con más de 11 500 Km de extensión de costas, que representan un importante recurso natural que puede ser aprovechado en el turismo; por lo anterior es importante investigar estructuras costeras que fomenten su conservación. Dentro de las estructuras empleadas, se encuentran los arrecifes artificiales que se han aplicado con gran éxito en varios paises para prevenir, preservar e incluso la reconstrucción y rehabilitación de playas. Para su aplicación es fundamental establecer los parámetros de diseño adecuados a las condiciones de oleaje a que serán sometidos, siendo el objeto del estudio determinar los coeficientes de transmisión de oleaje como indicador de su eficiencia.
El estudio se realizó en el Laboratorio de Ingeniería Hidráulica de la Escuela Superior de Ingeniería y Arquitectura-Unidad Zacateco del Instituto Politécnico Nacional de México, en su canal angosto con generador hidráulico de oleaje regular e irregular y equipo de medición de oleaje controlados por computadoras. En el canal se implementó un modelo físico reducido a una escala de líneas 1:20, de fondo fijo y sin distorsión, en el que se construyeron dos secciones de arrecife artificial de 34,00 m y 50,00 m de coronamiento en prototipo (1,70 m y 2,50 m en modelo).
Los ensayos se apoyaron en mediciones de oleaje incidente y transmitido sobre las dos diferentes secciones de arrecife calculándose los coeficientes de transmisión del oleaje, los cuales se contrastaron con las formulaciones de Goda et al. (1969), d´ Agremont et al. (1996), Van der Meer (1991, 2000 y 2004) y Armono (2003).
Análisis teórico
Transmisión del oleaje
Anteriormente se llevaron a cabo una serie de investigaciones de laboratorio para cuantificar el coeficiente de transmisión, se interpreta a través de la relación de la altura de ola incidente 𝐻𝑖, entre la altura de ola transmitida 𝐻𝑡 representado por la ecuación (1).
Donde:
K t |
coeficiente de transmisión |
H i |
altura de ola significante incidente |
H t |
altura de la ola transmitida |
Estas investigaciones produjeron fórmulas empíricas que se han utilizado ampliamente en la ingeniería de puertos y costas. Sin embargo, hay limitaciones a cada una de ellas debido a las condiciones de laboratorio y la gama de variables utilizados en las pruebas (Seabrook 1998).
Para una mejor interpretación del fenómeno de transmisión del oleaje sobre las estructuras estudiadas, se utilizaron los parámetros adimensionales que se consideran de mayor influencia para este fenómeno, los cuales se obtienen de relacionar las principales características de la estructura y del oleaje que incide sobre ella.
Varias investigaciones experimentales se realizaron en el pasado que condujo a expresiones semi-empíricas para el coeficiente de transmisión en oleaje irregular como son: Saville (1963), Goda (1969), Allsop (1983), Ahrens (1987), Van der Meer (1988, 1990, 1991, 2004), d'Angremond (1996), Van Der Meer y de Jong (1996).
De las fórmulas desarrolladas por investigadores, las propuestas para el estudio fueron las ecuaciones 2, 3, 4, 5 y 6:
Donde las variables de las ecuaciones tienen el siguiente significado:
K t |
Coeficiente de transmisión |
B |
Ancho del coronamiento de la estructura |
R c |
Bordo libre o sumergencia |
D |
Profundidad |
H |
Altura de la estructura |
H s |
Altura de ola incidente |
T i |
Período de la ola incidente |
H i /L |
Relación de esbeltez de ola incidente |
d/L |
Profundidad relativa |
B/L |
Ancho de coronamiento relativo |
R c /H s |
Profundidad de sumergencia relativa |
α |
2 y β tiene valores de 0,1 (alto), 0,3 (medio) y 0,5 (bajo) |
Parámetros considerados en el estudio
Oleaje incidente
Con base a datos de oleaje normal y de tormenta que corresponde a olas generadas en mar abierto, se realizó una propagación del oleaje hacia las profundidades a reproducir en el modelo. De acuerdo con lo anterior, se calcularon las características del oleaje a una profundidad de 10 m a pie del generador de oleaje (condición de modelo), y 4 m de profundidad en donde se desplantó el arrecife artificial.
Niveles del mar
El estudio considera la condición del oleaje normal y de tormenta, el plano de referencia fue el Nivel de Bajamar Media (N.B.M.).
Batimetría del modelo
Debido a las características experimentales del estudio y tomando en cuenta las pendientes de las playas del caribe mexicano, se representó un perfil playero con pendiente 1:20 donde se desplantaron las dos secciones del arrecife artificial a ensayar.
Secciones de arrecifes
Se propusieron 2 secciones de arrecifes artificiales de sección trapecial, con dimensiones de 34,00 y 50,00 m de coronamiento, altura de 2,50 m en promedio, con taludes 2:1 (lado mar y lado protegido), constituidos por enrocamiento en su capa secundaria y por elementos artificiales de concreto en su coraza (nuevo elemento propuesto) con peso de 2,5 toneladas.
Modelo hidraulico fisico
Escala del modelo
Para representar el fenómeno a reproducir en los ensayos, en este caso el comportamiento de las diferentes secciones de arrecifes artificiales bajo la acción de trenes de oleaje irregular, las fuerzas que imperan en el fenómeno de estudio son las gravitacionales y de inercia, por lo tanto, la condición de similitud a reproducir en el modelo es la de Froude (Hughes 1993). Con base en lo anterior, a las características de los oleajes y niveles a reproducir en las pruebas, y a los requerimientos del generador de oleaje irregular, se seleccionó una escala de líneas de 1:20, para un modelo de fondo fijo sin distorsión. De la escala anterior se determinaron las siguientes escalas de utilidad en el estudio, las cuales se resumen en la tabla 1.
Tabla 1 Escalas del modelo
| Tipo de escala. | Notación. | Escalas |
|---|---|---|
| Escala de líneas horizontales | ELH | 20,00 |
| Escala de líneas verticales | ELV | 20,00 |
| Escala de longitudes de ola | EL | 20,00 |
| Escala de alturas de ola | EH | 20,00 |
| Escala de periodos de ola | ET | 4,47 |
| Escala de celeridades de ola | EC | 4,47 |
| Escala de fuerzas | EF | 8 000 |
| Escala de pesos | EW | 8 000 |
Instalación
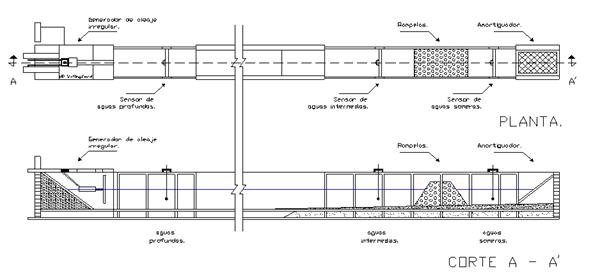
Los ensayos se llevaron a cabo en el canal de oleaje angosto del Laboratorio de Ingeniería Hidráulica de la Escuela Superior de Ingeniería y Arquitectura del Instituto Politécnico Nacional de México, con dimensiones de 24,45 m de longitud, 0,90 m de altura y 0,66 m de ancho; el cual cuenta con un generador hidráulico de oleaje regular e irregular en uno de sus extremos, cuyo control se efectúa por procedimientos electrónicos controlados por computadora. En el extremo contrario se colocó un amortiguador para absorber la energía del oleaje y limitar su reflexión. En el interior del canal, se realizó un relleno y colado de firmes para obtener dos pendientes del fondo marino, un tramo de 6,00 m con pendiente 1:20 y otro tramo de 9,00 m con pendiente 1:100. Se dispuso un tirante de agua a lo largo del canal de 0,50 cm (10,00 m en prototipo), tirante necesario para un adecuado funcionamiento del generador de oleaje. El canal de oleaje y la disposición del modelo ensayado se muestran en la figura 1.
Instrumentación
Para medir el oleaje incidiendo sobre el arrecife correspondiente, se colocaron tres sensores de oleaje de tipo resistivo para medir el oleaje en aguas profundas (pie del generador) y al pie de la estructura y posterior a la misma. Las señales analógicas transmitidas por los sensores de oleaje se amplificaron a través de un olómetro, para luego enviarse a un convertidor de señales A/D (analógico/digital) con que cuenta el equipo de cómputo; ya digitalizadas se analizaron con el programa de cómputo HR WAVES subrutina WARP (Beresford, 1994) y se enviaron a una impresora (figura 2).
Construcción del modelo
En el estudio se realizo la construcción de dos secciones de arrecife con anchos de coronamiento de 34,00 y 50,00 m. Los materiales de enrocamiento para el abilitado de las diferentes estructuras se obtuvo por medio de triturado (capa secundaria) y elementos artificiales fabricados de concreto (coraza) (ver figuras 3 y 4).
Procedimiento experimental
Calibración
En esta fase se llevaron a cabo una serie de ensayos para validar las señales de oleaje a reproducir en cada uno de los ensayos (cinco señales), así como la calibración de los sensores de oleaje de tipo resistivo a utilizarse en los ensayos. Este paso se realizó con el programa de cómputo HR WAVES, en la subrutina CAL.
Programa de ensayos
Para llevar a cabo las pruebas del modelo, se estableció el siguiente programa de ensayos (tabla 2):
Tabla 2 Programa de ensayos
| Señal | TPrototipo (seg) | Tmodelo (seg) | HPrototipo (m) | Hmodelo (cm) | Número de olas |
|---|---|---|---|---|---|
| 1 | 6,00 | 1,34 | 1,42 | 7,10 | 300 |
| 2 | 7,00 | 1,56 | 1,94 | 9,70 | 300 |
| 3 | 8,00 | 1,79 | 2,54 | 12,70 | 300 |
| 4 | 9,00 | 2,01 | 3,22 | 16,10 | 300 |
| 5 | 10,00 | 2,24 | 3,97 | 19,85 | 300 |
Condiciones y procedimiento de ensayos
Se utilizó el espectro frecuencial de Pierson - Moskowitz (el equipo cuenta con 7 espectros frecuenciales diferentes) para generar las señales de oleaje con el programa HR WAVEGEN subrutina SEASTATE (Beresford, 1994)
Cada sección se somete una incidencia total de 1.500 olas por serie de ensayos.
En todos los ensayos se mide el coeficiente de reflexión.
En todos los ensayos se mide el oleaje en dos puntos diferentes (al frente y en la parte posterior del arrecife)
Procedimiento de los ensayos
Ensayos para obtener coeficientes de reflexión
Con el objeto de conocer el grado de reflexión de los arrecifes artificiales, y en dado caso compensar las señales de oleaje, se procedió de la siguiente manera (Mansard and Funke 1980):
Se colocaron tres sensores de oleaje entre el generador de oleaje y el arrecife, a una distancia mayor de una longitud de ola (función está del período de oleaje correspondiente al ensayo) y separados entre sí de acuerdo con el período de oleaje de ensayo.
Se generó oleaje y se midió la energía de ola incidente y la reflejada en la estructura por cada uno de los tres sensores de oleaje.
Se calculó el coeficiente de reflexión promediando las energías del oleaje incidente y reflejado, evaluadas de los datos transmitidos por los sensores de oleaje al ológrafo y de ahí al programa HR WAVES subrutina REFLECTION con que cuenta el equipo de cómputo.
Ensayos para obtener coeficientes de transmisión
Estos se llevan a cabo mediante el proceso siguiente:
Se genera oleaje para cada uno de los ensayos, en tiempo suficiente para tener una incidencia de 300 olas sobre la estructura en prueba.
Cada estructura se somete a una incidencia total de 1 500 olas.
Con base en los datos de oleaje transmitidos por los sensores de oleaje y analizados por el programa HR WAVES subrutina WARP, se calculan las alturas y periodos de ola significante para cada ensayo.
En base a los datos obtenidos en el inciso anterior, se calculan los coeficientes de transmisión para cada uno de los ensayos.
Se realiza un registro de video y fotografías de cada ensayo.
Ensayos
En las figuras 5 y 6 se muestran dos de los ensayos realizados con las dos secciones de arrecifes.
Presentación de la información
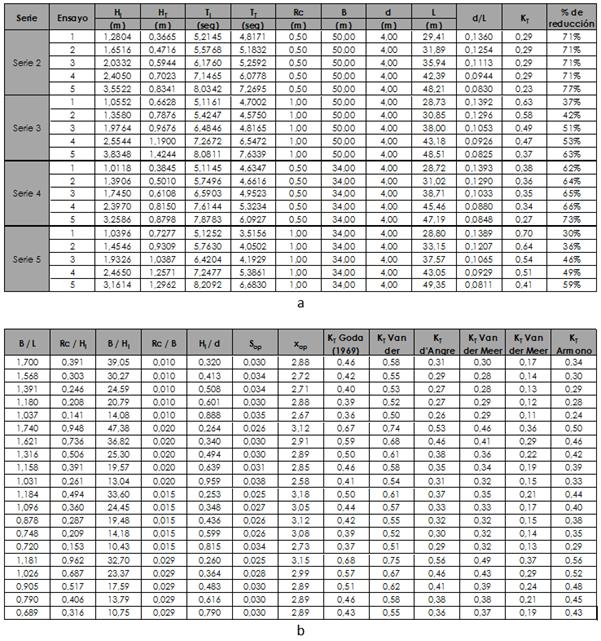
Se procedió a realizar el procesamiento de la información aportada por el estudio, obteniéndose los coeficientes de transmisión de acuerdo con los datos que, aportados por los ensayos y los coeficientes de transmisión obtenidos de las fórmulas de Goda (1969), d’Angremond (1996), Van der Meer (1991, 2000 y 2004) y Armono (2003).
Los datos de los ensayos de las dos secciones de arrecife artificial, así como los calculados con las fórmulas de los autores antes citados, se presentan en las figuras 7a y 7b.
Resultados
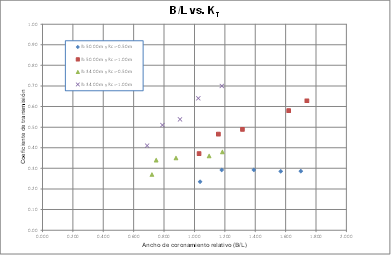
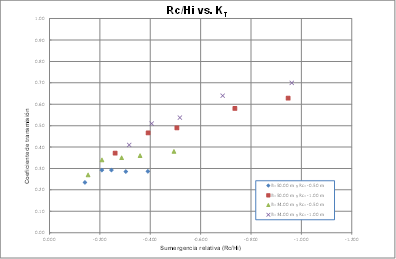
Se desarrollaron una serie de gráficas, en las cuales se representan los datos aportados por el estudio; en la primera se relacionan la sumergencia relativa del coronamiento contra el coeficiente de transmisión medido (ver figura 8), la segunda el ancho de coronamiento relativo contra el coeficiente de transmisión medido (ver figura 9) y en las tercera y cuarta, los coeficientes de transmisión calculados con respecto las fórmulas propuestas en las figuras 10 , 11, 12, 13, 14, 15, dichas gráficas se presentan a continuación.
Conclusiones
Teniendo en cuenta los resultados obtenidos, se puede concluir:
Se ensayaron dos estructuras con anchos de coronamiento de 34 y 50 m, con sumergencias de 0,50 y 1 m respectivamente. Con base en los resultados se concluye que la estructura que disipa mayor cantidad de energía del oleaje es la que presenta un ancho de coronamiento de 50 m y una sumergencia de 0,50 m, ya que sus coeficientes de transmisión se presentan en un rango de 0,23 a 0,29, siendo estos los valores más bajos obtenidos (ver figuras 8 y 9).
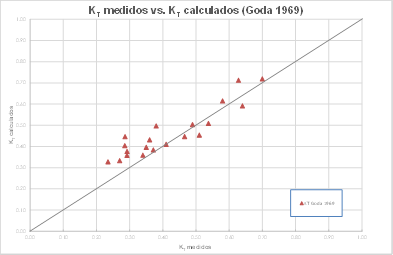
De la figura 10, donde se comparan los coeficientes de transmisión medidos contra los calculados con la fórmula de Goda (1969), se aprecia una dispersión baja de los datos con respecto a la recta de tendencia, siendo la fórmula de este investigador adecuada para evaluaciones de los coeficientes de transmisión en forma práctica.
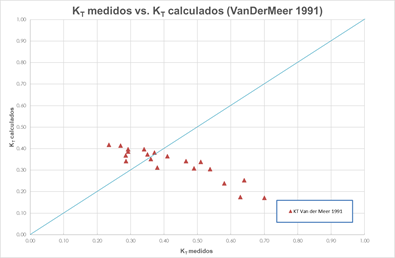
De la figura 11, donde se comparan los coeficientes de transmisión medidos contra los calculados con la fórmula de Van der Meer (1991), se observa una dispersión alta de los datos con respecto a la recta de tendencia, siendo la fórmula de este investigador no adecuada para evaluaciones de los coeficientes de transmisión en forma práctica.
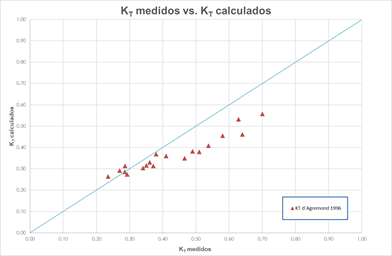
De la figura 12, donde se comparan los coeficientes de transmisión medidos contra los calculados con la fórmula de d´Agremond (1996), se advierte una dispersión media de los datos con respecto a la recta de tendencia, siendo la fórmula de este investigador no factible para evaluaciones de los coeficientes de transmisión en forma práctica.
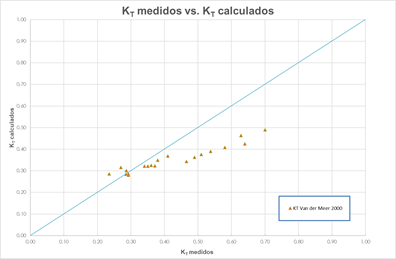
De la figura 13, donde se comparan los coeficientes de transmisión medidos contra los calculados con la fórmula de Van der Meer (2000), se nota una dispersión media de los datos con respecto a la recta de tendencia, siendo la fórmula de este investigador no adecuada para evaluaciones de los coeficientes de transmisión en forma práctica.
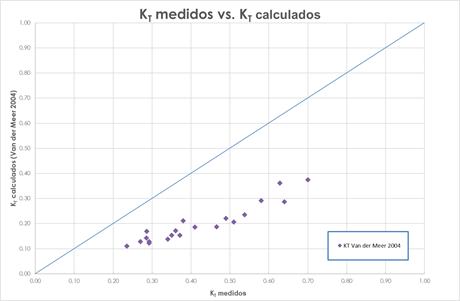
De la figura 14, donde se comparan los coeficientes de transmisión medidos contra los calculados con la fórmula de Van der Meer (2004), se percibe una dispersión alta de los datos con respecto a la recta de tendencia, siendo la fórmula de este investigador no recomendable para evaluaciones de los coeficientes de transmisión en forma práctica.
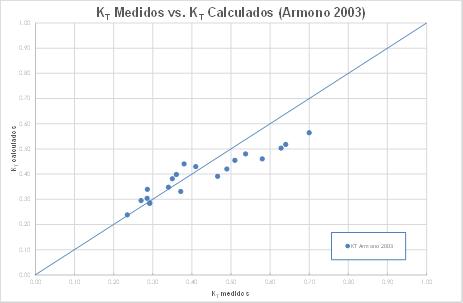
En la figura 15, donde se comparan los coeficientes de transmisión medidos contra los calculados con la fórmula de Armono (2003), se distingue también una dispersión reducida de los datos con respecto a la recta de tendencia, siendo la fórmula de este autor también adecuada para el cálculo de los coeficientes de transmisión.
Se concluye que las formulaciones que presentan una mejor tendencia en relación con los datos medidos fueron las propuestas por los autores Goda et al (1969) y Armono (2003), aunque también se analizaron las propuestas por d´Agremond (1996) y Van der Meer (1991, 2000 y 2004).
Finalmente, con base en los resultados producto del estudio, se puede concluir que los parámetros que tienen mayor influencia en la disminución de la transmisión del oleaje son la sumergencia y el ancho del coronamiento de los arrecifes artificiales (ver Figuras 8 y 9), lo cual concuerda con lo presentado en el estado del arte.