1.Introducción
La metaestabilidad es un fenómeno probabilístico que provoca fallos en sistemas digitales. Tiene mayor probabilidad de ocurrencia cuando un circuito recibe una señal asincrónica o se intercambian señales entre circuitos sincrónicos con dominios de reloj no relacionados. El riesgo también aumenta mientras mayor sea la frecuencia de reloj [1 4].
Para reducir la probabilidad de que la metaestabilidad se propague a través de un circuito y propiciar una transición más confiable de las señales entre los cruces de dominio de reloj, se recomienda el empleo de sincronizadores [5-8]. Según documentan Ginosar [5&093; y Golson [9], se utilizan soluciones de sincronización desde la década de 1940, la primera publicación sobre análisis matemático de la metaestabilidad y sincronizadores data de 1952, mientras que el primer trabajo experimental sobre este tema se reportó en 1973. En la literatura más reciente se presentan diversos circuitos de sincronización y protocolos de arbitraje, cuya selección depende de las características de los sistemas y de las frecuencias de los dominios de reloj involucrados. Entre los sincronizadores más utilizados se encuentra el de N flip-flops conectados en cascada, conocido también como de N etapas [7,9,10,11].
La efectividad de los sincronizadores puede expresarse mediante el parámetro MTBF (Mean Time Between Failure), que indica el tiempo medio entre fallas consecutivas y está relacionado con la fiabilidad del sistema [12]. El análisis del MTBF mediante métodos experimentales y de simulación ha sido centro de atención de grupos de investigación [13- 18] . Sin embargo, muchos reportes presentan un profundo nivel teórico y resulta trabajoso extrapolar los resultados a situaciones cotidianas relacionadas con el diseño lógico.
El desarrollo alcanzado en las tecnologías de fabricación de circuitos integrados ha permitido la construcción de dispositivos digitales CMOS cuyos transistores tienen largos de canal entre 130 nm y 14 nm [19,]. La disminución de las dimensiones hacia el orden de los nanómetros propicia la aparición de efectos que no eran apreciables a nivel de micrómetros y que influyen en el riesgo de metaestabilidad. Por ejemplo, las nuevas tensiones de alimentación son más cercanas a la tensión de umbral de los transistores [21] y en consecuencia se ha observado un cambio en el comportamiento de estos dispositivos ante variaciones de temperatura [25,]. El análisis del impacto que tienen la tecnología de fabricación, el potencial de la fuente de alimentación y la temperatura de trabajo (PVT: process, voltage and temperature) en los tiempos de respuesta de los nuevos dispositivos y en el riesgo de metaestabilidad, es de especial interés para la comunidad científica [22,23,27,28,29, 30].
La metaestabilidad no es un fenómeno teórico, es la causa real de los fallos de muchos circuitos digitales que funcionan correctamente a nivel de laboratorio. Es una necesidad que los diseñadores de sistemas electrónicos conozcan estos riesgos y desde la etapa de diseño, tomen las acciones para contrarrestarlos. Este trabajo tiene como objetivo analizar el comportamiento de la metaestabilidad en sincronizadores de dos etapas desarrollados sobre FPGA del fabricante Intel-Altera, específicamente de las familias Cyclone III y Cyclone V cuyas tecnologías son de 65 nm y 28 nm, respectivamente. Como método de investigación se utilizó la simulación basada en las herramientas de Quartus II y en modelos de los dispositivos para condiciones de operación extremas de PVT [31-33]. Las pruebas se realizaron en condiciones de temperaturas de trabajo correspondientes al rango industrial (-40 °C a 100 °C) y para diferentes frecuencias de reloj.
Como resultado se obtuvieron curvas que relacionan el MTBF de peor caso, la frecuencia de reloj del sincronizador y la temperatura. Se determinó que el MTBF de los sincronizadores varió con la temperatura de operación y lo hizo de manera diferente para los dispositivos de cada familia. Los resultados que se exponen constituyen un aporte de valor práctico al establecer las condiciones críticas de trabajo en función del riesgo de metaestabilidad y criterios de fiabilidad para los circuitos estudiados. Además, el artículo es una contribución a la divulgación de esta temática en nuestra comunidad científica.
2. Marco teórico
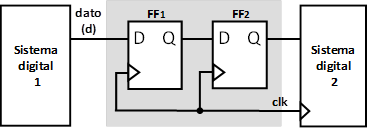
Los flip-flops constituyen la unidad básica de almacenamiento de los circuitos secuenciales sincrónicos. En un flip-flop tipo D, la señal del dato (D) tiene que estar estable por un tiempo mínimo antes (tiempo de set-up tsu) y después (tiempo de hold th) del frente de reloj para garantizar el correcto funcionamiento del circuito. La salida del flip-flop estará disponible después de un tiempo especificado por el fabricante (tco), como se muestra en la figura 1. Si se violan las condiciones de tiempo, el flip-flop puede caer en un estado metaestable [1]. Para que esta situación no se propague al resto del sistema y provoque una falla de sincronización, la metaestabilidad tiene que resolverse en un tiempo tMET [4].
En la figura 2 se muestra un sincronizador consistente en dos flip-flops conectados en cascada (dos etapas). Este circuito sincroniza la transferencia de datos (d) entre dos sistemas digitales con relojes no relacionados. Como se observa, el sincronizador y el sistema que recibe los datos operan con la misma señal de reloj (clk). Es un requisito para el correcto funcionamiento del sistema que el dato sea válido (se mantenga en nivel alto o en nivel bajo) durante al menos un período de reloj del sincronizador. Para lograr una mayor protección contra la metaestabilidad, se puede incrementar el número de flip-flops concatenados, pero aumentará también la latencia de la señal procesada [11]. Esta situación establece una solución de compromiso entre el comportamiento sin fallos del circuito en el tiempo y la latencia.
Si el primer flip-flop del sincronizador cae en metaestabilidad y el período de la señal de reloj es suficientemente grande, la salida inestable puede alcanzar un estado estable y no afectar al resto del circuito. Por lo tanto, considerar un tiempo adicional tMET para que la señal se establezca en un estado estable, evita la propagación de un valor desconocido al resto del sistema. Para una frecuencia de reloj dada (fclk), el tiempo disponible para resolver la metaestabilidad entre los dos flip-flops está determinado por:
La probabilidad de que el sincronizador de dos etapas de la figura 2 entre en el estado metaestable y permanezca en él un tiempo mayor que tMET, se calcula según la expresión 2 [2]:
En esta expresión, fd representa la frecuencia del dato de entrada al flip-flop. Una consideración importante para calcular el MTBF con la expresión 2, es que los datos sean asincrónicos o que se intercambien señales entre circuitos sincrónicos con dominios de reloj no relacionados [18]. Los parámetros C1 y C2 dependen del proceso tecnológico empleado en la fabricación del dispositivo, del valor de la fuente de alimentación y de la temperatura de operación. [2,34].
En los dispositivos digitales CMOS, el tiempo de resolución de la metaestabilidad depende de la velocidad de respuesta de sus transistores, lo que a su vez está influenciado por la tensión de alimentación y la temperatura de trabajo de los circuitos. Las expresiones 3 y 4 permiten analizar cómo estos dos últimos parámetros se relacionan con el tiempo de respuesta (td) y la corriente de drenaje (ID) del transistor MOS. La capacidad total equivalente de la carga a la salida del transistor está representada por Cout y VDD es la tensión de la fuente de alimentación. El potencial de umbral del transistor (VTH) y la movilidad de los portadores minoritarios en el canal de transistor (µ) tienen una relación inversa con la temperatura, o sea, decrecen con el aumento de la temperatura y viceversa [26].
En los transistores con largos de canal del orden de los micrómetros, la diferencia entre VDD y VTH es menos sensible a la temperatura, en comparación con la que experimenta la movilidad de los portadores minoritarios [22]. Como consecuencia, en esos transistores, la variación efectiva de la corriente ID con la temperatura queda dominada por la dependencia de la movilidad con la temperatura (µ(T)) [24]. Este comportamiento se refleja en el tiempo de respuesta del transistor, que tiende a ser más lento con el aumento de la temperatura.
En los dispositivos nanométricos, las tensiones de alimentación son del orden de 1 V y por lo tanto, más cercanos a la tensión de umbral (VTH) [21]. Consecuentemente, la diferencia VDD-VTH, se hace sensible a la influencia de la temperatura y puede dominar con respecto a la dependencia térmica de la movilidad de los portadores minoritarios en el canal del transistor. Es decir, cuando la temperatura fluctúa, los comportamientos de la corriente de drenaje y del tiempo de respuesta del transistor dependen del término que domine: si domina la dependencia de la movilidad, con el aumento de la temperatura, debe aumentar el tiempo de respuesta del transistor. Por el contrario, si domina la diferencia VDD-VTH, el incremento de la temperatura provocará la disminución de td. Este cambio del comportamiento que se pone de manifiesto en los nuevos dispositivos, conocido como inversión de la dependencia con la temperatura (ITD por sus siglas en inglés), afecta los parámetros de metaestabilidad.
Un sistema digital puede tener n sincronizadores. El valor efectivo del MTBF para este caso se determina mediante la expresión 5, donde el MTBF de cada sincronizador está representado por MTBFn [13,23]. De esta expresión se puede concluir que cuanto mayor sea la cantidad de sincronizadores en el circuito, mayor tiene que ser el valor del MTBF de cada sincronizador para lograr un MTBF efectivo requerido.
Mientras mayor sea el MTBF resultante del sistema, este será más fiable. La fiabilidad R(t) es la probabilidad de que un sistema o componente funcione satisfactoriamente, sin fallos, durante un período de tiempo (t). Si los fallos ocurren aleatoriamente, la fiabilidad puede ser descrita por la distribución exponencial de la expresión 6 [12]:
3. Materiales y métodos
El trabajo experimental consistió en determinar mediante simulación, los valores del MTBF de peor caso del sincronizador de dos etapas (figura 2) implementado en dispositivos FPGA de las familias Cyclone III (65 nm) y Cyclone V (28 nm) del fabricante Intel-Altera. El circuito sincronizador se describió en VHDL y para su síntesis se utilizó el programa Quartus II versión 13.0 sp1 (64-bits) de Intel-Altera.
Se utilizaron las herramientas de simulación de Intel-Altera, que disponen de modelos de los FPGA bajo estudio y que calculan la respuesta en el tiempo de los circuitos bajo diferentes condiciones extremas de PVT [33]. Los FPGA evaluados pueden operar en el rango industrial de temperatura de trabajo (-40 °C a 100 °C). Para las pruebas se seleccionaron los modelos slow -40°C, slow 0°C, slow 85°C y slow 100°C que para cada dispositivo tienen en cuenta los parámetros que producen la respuesta más lenta (slow) y consecuentemente, el peor MTBF. Estos modelos combinan las condiciones más limitadas del proceso de fabricación en el silicio (menor movilidad de los portadores minoritarios, mayor VTH, etc.), el valor mínimo permitido de la tensión de alimentación (1200 mV para la familia Cyclone III y 1100 mV para la familia Cyclone V) y la temperatura de la unión dentro del rango de trabajo de los dispositivos.
El análisis estático [35] de la respuesta en el tiempo en las peores condiciones de PVT, se realizó con la herramienta TimeQuest Analyzer del programa Quartus II [31]. Para obtener el reporte del MTBF, se simuló el sincronizador para cada modelo de cada dispositivo y para cada uno de los valores de frecuencia de la señal de reloj. Fue necesario también identificar el primer flip-flop del sincronizador y establecer la frecuencia de los datos (fd) a través del editor de asignaciones. Además, se aseguró que la opción de optimización de la metaestabilidad estuviera habilitada [32] con el objetivo de aprovechar toda la potencialidad de la herramienta.
En cada uno de los experimentos, la frecuencia de datos (fd) se fijó en 100 MHz, mientras que las frecuencias de reloj (fclk) se escogieron de modo que permitieran obtener valores cuantificables de MTBF de peor caso en los dispositivos de cada familia.
4. Discusión de los resultados
En un primer estudio se analizó el comportamiento de los valores de peor caso del MTBF del sincronizador de dos etapas con frecuencia de reloj de 250 MHz, implementado en varios FPGA de una misma familia. Los dispositivos seleccionados tienen el mismo nivel de velocidad (speed grade 7) [33] y para la simulación se emplearon sus correspondientes modelos para condiciones extremas de PVT a 0 °C (modelo slow 0° C). Los resultados obtenidos con los seis dispositivos evaluados de la familia Cyclone III se muestran en la figura 3. Los valores de MTBF estuvieron entre 203 000 y 208 000 años, mientras que la mayor variación con respecto al promedio fue de 1.5 %.

Fig. 3 Peor caso de MTBF de sincronizador de dos etapas implementado en dispositivos de la familia Cyclone III (fd=100 MHz, fclk = 250 MHz, modelo slow 0°C).
Los resultados obtenidos con dispositivos de la familia Cyclone V se presentan en la figura 4. En este caso los valores de MTBF estuvieron entre 8.09 y 9.06 años. La mayor variación con respecto al valor medio fue de 6.4 %. Dado que el MTBF es un índice estadístico que representa el tiempo promedio entre fallos, estos porcientos de variación no tienen efectos prácticos significativos. A partir de estos resultados se decidió que cualquiera de los dispositivos evaluados podía utilizarse en los futuros estudios de este trabajo.
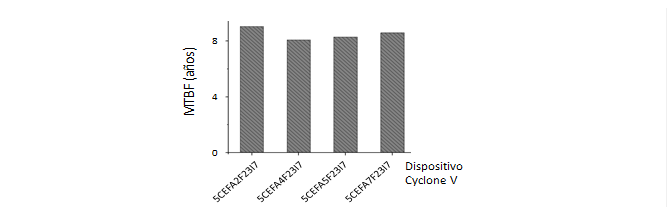
Fig. 4 Peor caso de MTBF de sincronizador de dos etapas implementado en dispositivos de la familia Cyclone V (fd=100 MHz, fclk = 250 MHz, modelo slow 0°C).
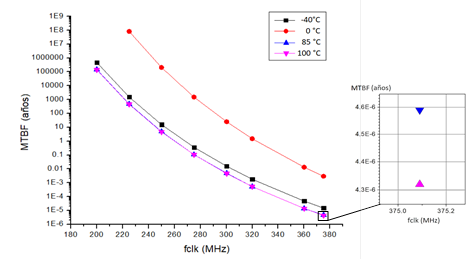
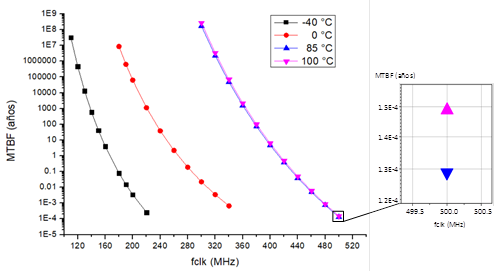
Para evaluar la relación entre la metaestabilidad, la frecuencia de la señal de reloj del sincronizador y la temperatura, se realizaron simulaciones con los dispositivos EP3C25F324I7 (Cyclone III - 65 nm) y 5CEFA2F23I7 (Cyclone V - 28 nm). En las figuras 5 y 6 se presentan gráficamente los resultados de MTBF de peor caso obtenidos en estos experimentos. El eje vertical tiene escala logarítmica. En todos los casos el MTBF decreció con el aumento de la frecuencia de reloj del sincronizador, lo que está en correspondencia con la expresión 2. También se aprecia que existe una dependencia entre el MTBF y la temperatura, aunque este comportamiento fue diferente para cada dispositivo.
Al comparar las curvas del EP3C25F324I7 correspondientes a cada modelo de temperatura (figura 5) se puede ver que, para una frecuencia dada, los menores valores de MTBF se obtuvieron a 100 °C. A medida que disminuye la temperatura hasta 0 °C, va aumentando el MTBF, o sea, disminuye el riesgo de que el circuito sufra metaestabilidad. Sin embargo, la curva correspondiente a la temperatura de -40 °C muestra valores de MTBF menores que la de 0 °C. Este comportamiento pudiera estar relacionado con la influencia que tiene la temperatura en el tiempo de respuesta de los transistores del dispositivo, ya que, a mayor velocidad de respuesta menos probabilidad tiene un circuito de fallar por metaestabilidad. El incremento del MTBF al disminuir la temperatura de 100 °C a 0 °C, sugiere un incremento de la velocidad de respuesta del dispositivo, probablemente debido al predominio de la dependencia con la temperatura de la movilidad de los portadores minoritarios del canal de los transistores. La disminución del MTBF observada a -40 °C, pudiera ser una manifestación del fenómeno conocido como inversión de la dependencia con la temperatura.
Para el sincronizador sintetizado en el FPGA 5CEFA2F23I7 de la familia Cyclone V (figura 6), el mayor valor de MTBF se obtuvo a 100 °C y al contrario de lo que sucedió en el dispositivo de la familia Cyclone III, según baja la temperatura el MTBF disminuye, o sea, aumenta la probabilidad de ocurrencia de metaestabilidad. Estos resultados reflejan que, con la disminución de la temperatura, se acortó el tiempo de respuesta del dispositivo, lo que indica que este último parámetro estuvo controlado por la dependencia térmica del potencial de umbral de los transistores. Puede concluirse que en el dispositivo con transistores con largo de canal de 28 nm se ha manifestado el comportamiento de inversión de la dependencia con la temperatura.
Conocer el MTBF es imprescindible para determinar la fiabilidad de un circuito electrónico durante un tiempo de operación de interés. Si la metaestabilidad fuera la única causa de fallo, los resultados mostrados en las figuras 5 y 6 permiten, a partir de un criterio de fiabilidad, determinar la máxima frecuencia de reloj permisible del sincronizador de dos etapas según la temperatura de trabajo. Igualmente, se puede determinar la fiabilidad a partir de la frecuencia de reloj y de la temperatura de operación.
Por ejemplo, si para el sincronizador de dos etapas que se evalúa en este trabajo se considera un 90% de probabilidad de funcionar correctamente durante un tiempo de operación de 10 años, el MTBF debe ser como mínimo igual a 100 años. Bajo esas condiciones, para el circuito sintetizado en el FPGA de la familia Cyclone III, la máxima frecuencia de reloj permisible en todo el rango industrial de temperatura es cercana a 225 MHz. Este valor queda determinado por la peor condición (100 °C). Al realizar un análisis similar con el FPGA de Cyclone V, puede observarse que la peor condición ocurre a -40 °C. Ese caso determina que, para operar en todo el rango industrial de temperatura, la frecuencia máxima de reloj queda limitada a 150 MHz. A esa frecuencia no se garantiza que el dato esté válido durante un período del reloj. Esta situación conllevaría al diseñador a replantearse la selección de otra familia de dispositivos si se precisa operar en todo el rango industrial de temperatura de trabajo. Sin embargo, es interesante que para las temperaturas de 85 °C y 100 °C sí se logra con este FPGA la fiabilidad del 90 % en 10 años a frecuencias de reloj de hasta 380 MHz, superiores a las alcanzadas con el Cyclone III.
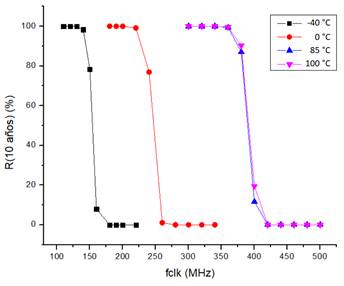
Estos resultados se corroboran al analizar las curvas que se presentan en las figuras 7 y 8, donde en el eje vertical se ha representado la fiabilidad del circuito en 10 años. En estas gráficas puede apreciarse que, para cada condición de temperatura, se logra una fiabilidad superior al 90 % para las menores frecuencias de reloj. En estos casos es donde se cumplen las condiciones de tiempo (tsu, th) de los flip-flops del circuito con mayor probabilidad y consecuentemente es menor el riesgo de metaestabilidad. Cuando el valor de la frecuencia de reloj supera un valor límite, la fiabilidad desciende bruscamente alcanzando valores inferiores al 20 %, puesto que el riesgo de fallos ha aumentado. Este comportamiento debe tenerse en cuenta como criterio de diseño, de modo que la frecuencia de reloj establecida en las especificaciones del circuito cumpla con el MTBF requerido. Si el diseño analizado tiene dos sincronizadores idénticos, según la expresión 5, el MTBF de cada sincronizador para el caso analizado anteriormente debe ser de 200 años.
5. Conclusiones
En este trabajo se presentó el estudio del comportamiento de la metaestabilidad en sincronizadores de dos etapas desarrollados sobre FPGA de las familias Cyclone III (65 nm) y Cyclone V (28 nm) del fabricante Intel-Altera, a partir de pruebas de simulación basadas en las herramientas de Quartus II y en modelos de los dispositivos para condiciones de operación extremas de PVT. Se obtuvieron curvas que relacionan el MTBF de peor caso, la frecuencia de reloj del sincronizador y la temperatura. Se determinó que el MTBF varió con la temperatura de operación en el rango industrial de trabajo (-40 °C a 100 °C) y lo hizo de manera diferente para los dispositivos de cada familia, poniéndose de manifiesto también el impacto de la tecnología en el riesgo de metaestabilidad. En el Cyclone III aumentó el MTBF al disminuir la temperatura de 100 °C a 0 °C y luego disminuyó para -40 °C, este cambio de comportamiento para la menor temperatura se atribuyó a la ocurrencia del fenómeno ITD. En el dispositivo Cyclone V disminuyó el MTBF al bajar la temperatura, poniéndose de manifiesto el fenómeno ITD en todo el rango estudiado. Los resultados presentados constituyen un aporte de valor práctico al permitir, para los circuitos estudiados, establecer las condiciones críticas de trabajo en función del riesgo de metaestabilidad y de criterios de fiabilidad.