ARTÍCULO ORIGINAL

 

Representación del desarrollo de la espongiosa primaria por medio de un sistema de reacción-difusión: Una hipótesis sobre el inicio de la formación de hueso inmaduro. Parte 2: Implementación numérica

 

Representation of the development of the primary spongiosa by means of a reaction-diffusion system: a hypothesis on the onset of immature bone formation. Part 2: Numerical implementation

 

 

MsC. Oscar Rodrigo López-Vaca,^I Ing. Diego Alexander Garzón-Alvarado^II

^IFacultad de Ingeniería Mecánica, Universidad Santo Tomás. Bogotá, Colombia.
^IIDepartamento de Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia. Bogotá, Colombia.

 

 

---

RESUMEN

Se presenta la implementación numérica del modelo bioquímico descrito mediante el sistema de reacción-difusión de la parte 1. De los resultados obtenidos se puede concluir que la retroalimentación química de los 2 factores moleculares a través de un sistema de reacción-difusión (RD) con parámetros en el espacio de Turing, puede explicar la aparición de los patrones espacio-temporales encontrados en la arquitectura de la espongiosa primaria. Para la solución numérica fue usado el método de los elementos finitos junto con el método de Newton-Raphson para aproximar las ecuaciones diferenciales parciales lineales. Los patrones de osificación obtenidos pueden representar la formación de la espongiosa primaria durante la osificación endocondral.

Palabras clave: espongiosa primaria, osificación endocondral, sistemas de reacción-difusión, simulación por elementos finitos.

---

ABSTRACT

A presentation is made of the numerical implementation of the biochemical model described by means of the reaction-diffusion system in Part 1. Based on the results obtained it may be concluded that the chemical feedback of the two molecular factors by means of a reaction-diffusion (RD) system with Turing space parameters may explain the appearance of the spatio-temporal patterns found in the architecture of the primary spongiosa. For the numerical solution, use was made of the finite element method in combination with the Newton-Raphson method to approximate the linear partial differential equations. The ossification patterns obtained may represent the formation of the primary spongiosa during endochondral ossification.

Key words: primary spongiosa, endochondral ossification, reaction-diffusion systems, finite element simulation.

---

 

 

INTRODUCCIÓN

Muchos problemas físicos pueden modelarse haciendo uso del balance de dos fenómenos: la difusión y la reacción.^1,2 La primera se define como la dispersión de las sustancias involucradas en el proceso a lo largo del dominio físico del problema; y la reacción, como el proceso de interacción mediante el cual se generan o se consumen las especies involucradas en el fenómeno. Matemáticamente, el problema de reacción-difusión se expresa mediante un conjunto de ecuaciones que contienen expresiones que describen los reactivos de concentración, los reactivos de difusión y un término que representa y describe la interacción no lineal entre los reactivos (ecuaciones 1).

El conjunto de ecuaciones de reacción-difusión donde intervienen más de un reactante, tienen la habilidad de crear determinados patrones espacio-temporales. Un caso particular son las inestabilidades de Turing^2-6 caracterizadas por la aparición de patrones formados por la concentración de las especies dentro del dominio, los cuales son estables en el tiempo e inestables en el espacio. Este tipo de modelos matemáticos han inspirado modelos para el estudio de diferentes problemas como transferencia de calor,⁷ biología,^4,5,8-11 ingeniería biomédica,^1,8,9,12 entre otros. El análisis de estos sistemas de reacción-difusión con inestabilidades de Turing, se ha desarrollado desde 2 marcos de trabajo: análisis matemático,¹³ y simulación numérica.^2,4-6,14,15 Desde la perspectiva analítica el trabajo se ha centrado en entender el comportamiento de los sistemas de reacción-difusión estudiando la relación entre las bifurcaciones del espacio de parámetros y la formación de patrones.

La simulación numérica de los sistemas de reacción-difusión ha permitido comprobar el conocimiento obtenido analíticamente sobre la formación de patrones, como por ejemplo, los trabajos de Madzvamuse y otros,^4,5 Maini y otros,^8,9 Murray y otros¹⁶ y Garzón y otros,^{1,2,6,12,14,15} donde se han desarrollado ejemplos numéricos sobre la formación de patrones en dominios en 2 y 3 dimensiones, teniendo en cuenta consideraciones de dominio creciente.

De acuerdo con esto, esta segunda parte presenta la simulación numérica de sistema de ecuaciones de reacción-difusión que representan la interacción de los 2 factores moleculares como el VEGF y el MMP13, solucionados mediante el método de los elementos finitos junto con el método de Newton Raphson. Este sistema de ecuaciones de reacción-difusión con parámetros en el espacio de Turing permite suponer que hay una interacción controlada entre 2 factores moleculares que da paso a la aparición de patrones espacio-temporales similares a los que se encuentran en la arquitectura de la espongiosa primaria durante el proceso de osificación endocondral.

 

MÉTODOS

A. Estimación de parámetros del modelo

 

 

 

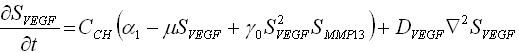
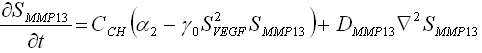
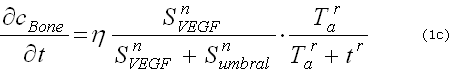
El conjunto de ecuaciones (1) corresponden a un sistema acoplado donde las ecuaciones correspondientes a los factores moleculares (1a) y (1b) son ecuaciones de reacción-difusión ampliadas, similares a un sistema de Turing que presenta una difusión controlada por inestabilidades. Para , la difusión controlada por inestabilidades aparece para cierta combinación de parámetros,^5,12,17 esto define un dominio en el espacio de los parámetros llamado espacio de Turing. Para obtener un espacio de Turing se necesita un análisis de estabilidad lineal del sistema de reacción-difusión sobre la solución homogénea, la cual es obtenida obligando a y , obteniendo . El análisis lineal permite encontrar los patrones espaciales de la solución linealizada y el rango de parámetros que garantizan la aparición de tales patrones específicos.⁵ Por lo tanto, la solución puede ser expresada como donde y son pequeñas perturbaciones en cada factor molecular, respectivamente. De las ecuaciones (1a) y 1(b) los resultados del análisis lineal permiten escribir las siguientes desigualdades:

 

 

 

 

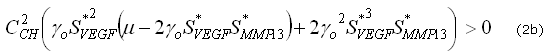
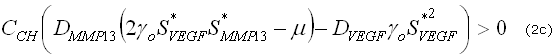
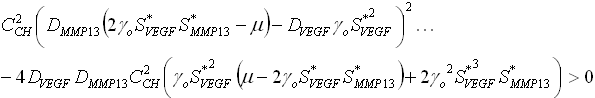
Estas desigualdades definen un dominio en el espacio de los parámetros, conocido como el espacio de Turing, donde el estado estable uniforme es linealmente inestable.

Si se expresan las ecuaciones (1a) y (1b) en una forma adimensional (ecuación de Schnakenberg) y en función de las pequeñas perturbaciones de los factores moleculares , respectivamente, a través de se puede obtener:

 

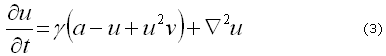
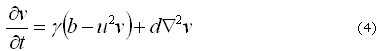
Donde pueden ser identificados los parámetros para el modelo y su relación:

 

 

 

 

 

 

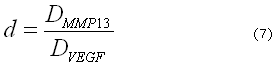
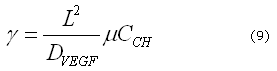
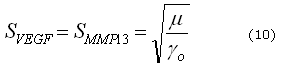
Donde es el tiempo característico del proceso biológico y es la longitud característica del modelo dimensional. Por lo tanto, definiendo es posible obtener los eigenvalores y los eigenvectores del conjunto de ecuaciones (3) y (4) y de ellos los diferentes patrones espaciales correspondientes a diferentes números de onda.

En el caso del modelo dimensional propuesto es necesario definir parámetros adimensionales . Para estimar estos valores se tienen en cuenta para este trabajo algunas evidencias experimentales:

- La concentración típica de VEGF en el tejido humano es de ¹⁸

- El dominio de estudio es un elemento tridimensional cúbico de lado ¹⁹

- La concentración de condrocitos hipertróficos en la epífisis femoral proximal ¹

- El coeficiente de difusividad para el VEGF es de ²⁰

Para reproducir los patrones presentes en la arquitectura del hueso trabecular primario con el modelo propuesto, es necesario que todos los parámetros se encuentren en el espacio de Turing y que con ellos se cumplan las restricciones (2). Por lo tanto, tomando los valores para , , y el conjunto de valores , , y^1,14 que cumplen con las restricciones de Turing y usando las relaciones de las ecuaciones (3) y (4) se obtiene el conjunto de valores que serán utilizados para la solución de las ecuaciones (1) (tabla).

 

B. Implementación numérica

El conjunto de ecuaciones (1) fueron implementadas y numéricamente solucionadas mediante el método de los elementos finitos con un esquema Newton-Raphson; para su solución se utilizó FORTRAN. El ejemplo propuesto se solucionó en un Laptop de 4 096 MB y 800 MHz de velocidad de procesador. La simulación computacional se llevó a cabo en un esquema iterativo incremental que permite solucionar, computacionalmente, la evolución tanto de la concentración de los factores moleculares como de la producción del hueso inmaduro. Inicialmente el cartílago de crecimiento es asumido como una matriz estructural con una concentración inicial de condrocitos en estado hipertrófico . Las concentraciones iníciales de VEGF y MMP13 se distribuyen aleatoriamente en el cartílago de crecimiento, con una perturbación del 10 % sobre la concentración de estado estable dada por . La selección de las condiciones iniciales aleatorias alrededor del estado estable es similar al evento de la expresión molecular de parte de los condrocitos hipertróficos en una zona de osificación. Las condiciones de flujo para cada factor molecular en la frontera se suponen nulas, esto debido a que estas condiciones se suponen periódicas sobre el dominio. Los valores de los parámetros utilizados se han mostrado previamente al igual que la justificación de todos los parámetros usados en los ejemplos ilustrados.

 

RESULTADOS

Para verificar el potencial del modelo propuesto en la predicción de la arquitectura de la espongiosa primaria, se realizó un ensayo numérico en un elemento cúbico tridimensional con una longitud de 0,2 mm. Los parámetros del modelo de reacción-difusión fueron seleccionados de forma tal que se obtuvieran estructuras con una periodicidad acorde con las presentes en el hueso trabecular.^19,21,22 En la malla de elementos finitos utilizada se emplearon 17 756 nodos y 16 625 elementos tetraedros. En todas las simulaciones se emplearon pasos incrementales de .

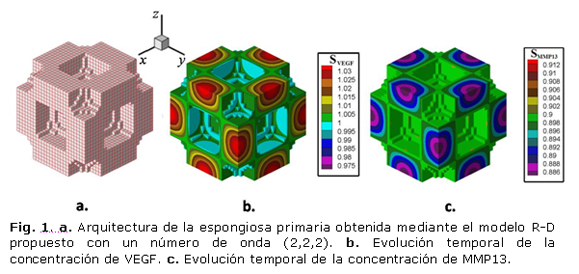
Como consecuencia de la interacción química entre los 2 factores moleculares (reactantes) y mediante los resultados numéricos fueron determinados patrones espaciales estables en el tiempo. La concentración de los factores moleculares en el cartílago y la acción del proceso difusivo permiten la formación de un patrón que se replica en todo el dominio. La arquitectura de la espongiosa primaria obtenida mediante el modelo R-D propuesto depende de los parámetros utilizados, por lo que se puede obtener estructuras con número de onda (2,2,2), como se muestra en la figura 1, en la que se observa la formación de dos medias ondas en cada una de las direcciones x, y y z.

 

 

Las figuras 1b, y 1c muestran los resultados para la organización del VEGF y MMP13 luego de la estabilización del proceso de reacción-difusión, nótese que en las zonas de mayor concentración de VEGF se produce calcificación del cartílago y en aquellas zonas de mayor presencia de MMP13 se produce su degradación (espacio vacío).

La arquitectura de la espongiosa primaria en un elemento cúbico de longitud 0,44 mm, como se muestra en la figura 2, donde se observan los patrones regulares para el modo de onda (2,2,2). De igual forma se puede ver el avance del frente de osificación en diferentes instantes, permitiendo la invasión del cartílago por células osteogénicas y condrogénicas que producen su degradación y calcificación. De esta forma se promueve la formación de las trabéculas primarias, las cuales posteriormente se someterán a procesos de remodelado óseo, producto de la distribución de los esfuerzos sobre el tejido óseo.

 

DISCUSIÓN

Mucho se ha aprendido en los últimos años acerca de los mecanismos celulares y moleculares que orientan los diferentes eventos que permiten la producción de hueso inmaduro por medio del mecanismo de osificación endocondral.^20,21,23-33 No obstante, aún existen inquietudes acerca de la relación e interacción de los diferentes eventos para permitir la osificación y crecimiento endocondral.

El trabajo presentado en esta segunda parte ilustra y da soporte a la validez de los modelos de reacción-difusión para describir los procesos ocurridos durante un evento complejo de formación de patrones en la biología del hueso. De los resultados presentados se puede concluir que la retroalimentación química entre los dos factores moleculares reactantes (activador-sustrato), pueden ser la mayor causa de la producción de los complejos patrones espaciales estables encontrados en el origen de la arquitectura de la espongiosa primaria, la cual es altamente estable y repetible. De igual forma estos factores pueden dar explicación al tamaño y forma tanto de las trabéculas como de los poros presentes en este tejido. Sin embargo, es claro que estos resultados han sido obtenidos con un modelo matemático basado en suposiciones y simplificaciones que deben ser discutidas. De igual forma, como cualquier otro sistema físico, el sistema biológico modelado está sometido a diferentes perturbaciones que pueden cambiar el patrón establecido por el modelo aquí planteado.

La producción de factores moleculares que actúan como activador-sustrato mediante la diferenciación de condrocitos prehipertróficos, no necesariamente son los únicos factores expresados por estas células condrogénicas, que probablemente afectan considerablemente el proceso de osificación, incluso los condrocitos no son las únicas células que actúan en este proceso. Sin embargo, el modelo planteado solo se enfoca en la formación de la arquitectura de la espongiosa primaria y no en el proceso de calcificación completo, en el cual también actúan células óseas como los osteoclastos y los osteoblastos. Para este último caso el modelo no solo incorpora influencias químicas (modelo biorregulatorio), probablemente involucre cargas y restricciones en la frontera (efectos mecánicos), así como otros factores bioquímicos adicionales que se deberá tener en cuenta.

Por último, a pesar de todas las limitaciones y simplificaciones el modelo matemático propuesto es capaz de reproducir con detalle la arquitectura de la espongiosa primaria, permitiendo la variación en la porosidad y el espesor de las trabéculas. El modelo propuesto servirá como base para determinar la formación de la arquitectura de la espongiosa secundaria, a partir del proceso de remodelado óseo, contemplando la acción de las células óseas y los diferentes efectos mecánicos que determinan la orientación de las trabéculas.

 

REFERENCIAS BIBLIOGRÁFICAS

1. Garzón-Alvarado DA, García-Aznar JM, Doblaré M. A reaction-diffusion model for long bones growth. Biomechanics and modeling in mechanobiology. 2009;8:381-95.

2. Garzón-Alvarado DA, Galeano Urueña CH. Mantilla González, JM. Ensayos numéricos sobre la formación de patrones de Turing bajo la acción de campos convectivos incompresibles: un acercamiento desde el problema de la cavidad. Ingeniería. 2010;14:239-60.

3. Turing AM. The Chemical Basis of Morphogenesis. Biological Sciences. 1952;237:37-72.

4. Madzvamuse A. A moving grid finite element method applied to a model biological pattern generator. Journal of Computational Physics. 2003;190: 478-500.

5. Madzvamuse A. Maini PK, Wathen AJ. A moving grid finite element method for the simulation of pattern generation by Turing models on growing domains. Journal of Scientific Computing. 2005;24:247-62.

6. Garzón-Alvarado DA, Galeano, CH, Mantilla JM. Turing pattern formation for reaction-convection-diffusion systems in fixed domains submitted to toroidal velocity fields. Applied Mathematical Modelling. 2011;35:4913-25.

7. Talayakyildiz F, Bellout H. Chaos in the thermal convection of a Newtonian fluid with a temperature dependent viscosity. Applied Mathematics and Computation. 2005;162:1103-18.

8. Maini PK. Mathematical models in morphogenesis. Mathematics inspired by biology. 1999;40:151-89.

9. Maini PK, Painter KJ, Nguyen Phong Chau H. Spatial pattern formation in chemical and biological systems. Journal of the Chemical Society, Faraday Transactions. 1997;93:3601-10.

10. Meinhardt H, Gierer A. Application of a theory of biological pattern formation based on lateral inhibition. Cell Science. 1974;15:321-46.

11. Vanegas J, Landinez N, Garzón D. Analysis of Turing instability in biological models. DYNA. 2009;123-34.

12. Garzón-Alvarado, DA. García-Aznar JM, Doblaré M. Appearance and location of secondary ossification centres may be explained by a reaction-diffusion mechanism. Computers in biology and medicine. 2009;39:554-61.

13. Mei Z. Numerical bifurcation analysis for reaction-diffusion equations. Berlin, Germany: Springer-Verlag; 2000. p. 428.

14. Garzón-Alvarado, DA, Velasco MA, Narváez-Tovar CA. Self-assembled Scaffolds using reaction-diffusion systems: a hypothesis for bone regeneration. Journal of Mechanics in Medicine and Biology. 2011;11:231.

15. Garzón-Alvarado DA, Ramírez Martinez AM. A biochemical hypothesis on the formation of fingerprints using a turing patterns approach. Theoretical biology & medical modelling. 2011;8:24.

16. Murray JD. Pattern formation in integrative biology: a marriage of theory and experiment. Comptes Rendus de l'Académie des Sciences. Series III. Sciences de la Vie. 2000;323:5-14.

17. Cramping EJ, Maini PK. Reaction-diffusion models for biological pattern formation. Methods and applications of analysis. 2001;8:415-28.

18. Hiltunen MO, Ruuskanen M, Huuskonen J, Mähönen AJ, Ahonen M, Rutanen J, et al. Adenovirus-mediated VEGF-A gene transfer induces bone formation in vivo. The FASEB journal: official publication of the Federation of American Societies for Experimental Biology. 2003;17:1147-9.

19. Ruimerman R, Hilbers P, Rietbergen BV, Huiskes R. A theoretical framework for strain-related trabecular bone maintenance and adaptation. Journal of Biomechanics. 2005,38:931-41.

20. Brouwers JEM, Van Donkelaar CC, Sengers BG, Huiskes R. Can the growth factors PTHrP, Ihh and VEGF, together regulate the development of a long bone? Journal of biomechanics. 2006;39:2774-82.

21. Olszta MJ, Xingguo C, Sang SJ, Rajendra K, Yi-Yeoun K, Kaufman MJ, et al. Bone structure and formation: A new perspective. Materials Science and Engineering: Reports. 2007;58:77-116.

22. Segre GV, Lee K. Endochondral Bone Formation Regulation by Parathyroid Hormone-Related Peptide. Indian Hedgehog and Parathyroid Hormone. The Parathyroids: Basic and Clinical Concepts. 2001;245-60.

23. Ballock RT, O'Keefe RJ. The biology of the growth plate. The Journal of bone and joint surgery. American volume. 2003;85-A:715-26.

24. Blumer MJF, Longato S, Fritsch H. Structure, formation and role of cartilage canals in the developing bone. Annals of anatomy. 2008;190:305-15.

25. Carlevaro MF, Cermelli S, Cancedda R, Descalzi Cancedda F. Vascular endothelial growth factor (VEGF) in cartilage neovascularization and chondrocyte differentiation: auto-paracrine role during endochondral bone formation. Journal of cell science. 2000;113(Pt 1):59-69.

26. Carter DR, Van der Meulen MC, Beaupré GS. Mechanical factors in bone growth and development. Bone. 1996;18:5S-10S.

27. de Crombrugghe B, Lefebvre V, Behringer RR, Bi W, Murakami S, Huang W. Transcriptional mechanisms of chondrocyte differentiation. Matrix biology. Journal of the International Society for Matrix Biology. 2000;19:389-94.

28. Crombrugghe B, Lefebvre V, Nakashima K. Regulatory mechanisms in the pathways of cartilage and bone formation. Current Opinion in Cell Biology. 2000;13:721-27.

29. Huch K, Kleffner S, Stöve J, Puhl W, Günther KP, Brenner RE. PTHrP, PTHr, and FGFR3 are involved in the process of endochondral ossification in human osteophytes. Histochemistry and cell biology. 2003;119:281-7.

30. Mackie EJ, Ahmed YA, Tatarczuch L, Chen KS, Mirams, M. Endochondral ossification: how cartilage is converted into bone in the developing skeleton. The international journal of biochemistry & cell biology. 2008;40:46-62.

31. Ortega N, Behonick DJ, Zena W. Matrix remodeling during endochondral ossification. Trends in Cell Biology. 2004:14:8.

32. Provot S, Schipani E. Molecular mechanisms of endochondral bone development. Biochemical and biophysical research communications. 2005;328:658-65.

33. Yang X, Karsenty G. Transcription factors in bone?: developmental and pathological aspects. Trends in Molecular Medicine. 2002;8:340-45.

 

 

Recibido: 5 de septiembre de 2011.
Aceptado: 22 de septiembre de 2011.

 

 

Oscar Rodrigo López-Vaca. Facultad de Ingeniería Mecánica, Universidad Santo Tomás. Bogotá, Colombia. Correo electrónico: [e-mail]