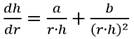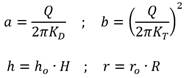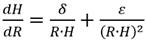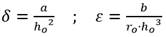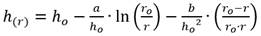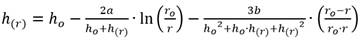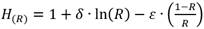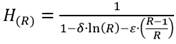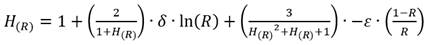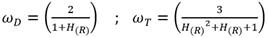Introducción
La ecuación diferencial obtenida por Pérez Franco (1982), que modela el flujo no lineal permanente en los acuíferos libres no había sido integrada en cuadraturas para su momento, ya que dicha ecuación no tiene solución analítica exacta, por lo tanto, hace algún tiempo Bravo Castillero (1993) integró en cuadraturas dicha ecuación, introduciendo una nueva relación y obteniendo dos soluciones utilizando métodos numéricos.
La primera solución la obtuvo mediante el método de aproximaciones sucesivas donde el primer término de la sucesión de funciones de Picard coincide con la solución propuesta en un principio por Pérez Franco (1982), la segunda solución fue obtenida mediante una aproximación asintótica basado en el método de perturbaciones regulares en relación con un parámetro pequeño.
Ahora bien, Bravo Castillero (1993, 1994), realiza diversos juegos de datos y concluye que la solución dada por la aproximación asintótica resulta bastante similar a la solución propuesta en un principio por Pérez Franco, sin embargo, Bravo Castillero recomienda utilizar la aproximación asintótica; debido a que garantiza errores del orden ε^2 y ε, ya que al utilizar la solución propuesta por Pérez Franco es difícil acotar y precisar el error que se comete, asimismo, dicho error será menor en los casos en que ε y δ se aproximen a cero, según la propuesta de Pérez Franco.
Por otro lado, el autor en un trabajo anterior (2022), obtuvo una solución analítica apoyada en los trabajos de Huyakorn y Dudgeon (1976), no obstante, resulta necesario validar las diferentes expresiones obtenidas, solucionando por el método de Runge Kutta cuarto orden la ecuación diferencial ordinaria obtenida por Pérez Franco.
Ecuaciones derivadas para los acuíferos libres en régimen no lineal
Antes que nada, no es ocioso mencionar y recordar las diversas restricciones impuestas por diversos investigadores al analizar el flujo radial hacia un pozo en un acuífero libre. Por consiguiente; para un acuífero libre, Pérez Franco (1982) obtuvo la siguiente formulación:
Ahora bien, Bravo Castillero (1993) propuso las siguientes transformaciones:
Por consiguiente, se obtiene la siguiente expresión adimensional para la ecuación (1):
Ahora, según las formulaciones obtenidas respectivamente por Pérez Franco (1982), Bravo Castillero (1993) y Rincón (2022), se tiene que:
Pero, si se ajustan las formulaciones anteriores respectivamente, teniendo en cuenta las relaciones dadas en la ecuación (2), se obtiene que:
Donde:
Q |
caudal de bombeo. |
ho |
espesor inicial del acuífero. |
h(r) |
espesor del acuífero a la distancia radial r. |
ro |
radio de influencia. |
r |
distancia en la cual se evalúa h_((r)). |
KD |
conductividad hidráulica lineal. |
KT |
conductividad hidráulica turbulenta. |
Validación de las expresiones obtenidas
Antes que todo, resulta importante analizar las transformaciones realizadas por Bravo Castillero (1993) que condujeron a la ecuación (3). Si se realiza un análisis somero a los términos a y b, se puede concluir con bastante facilidad que b > a y; por deducción, ε < δ. Ahora, la simulación de la ecuación (3) mediante el método numérico de Runge Kutta cuarto orden se realizó con Macros de Excel y Python, por consiguiente, se realizaron un grupo de simulaciones cuyos parámetros se resumen en la tabla 1.
Tabla 1 Parámetros de la simulación
| Parámetros de entrada | Simulación | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| h | 50 | 50 | 50 | 200 | 200 | 200 | 1000 |
| a | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| b | 50 | 50 | 50 | 2 | 2 | 50 | 50 |
| δ | 0,027777778 | 0,111111111 | 0,0025 | 0,04 | 0,000369822 | 0,000816327 | 0,000452694 |
| ε | 0,023148148 | 0,185185185 | 0,0000625 | 0,001066667 | 5,68958 x10-8 | 9,71817x10-6 | 1,20397x10-6 |
| ho(m) | 6 | 3 | 20 | 5 | 52 | 35 | 47 |
| ro (m) | 10 | 10 | 100 | 15 | 250 | 120 | 400 |
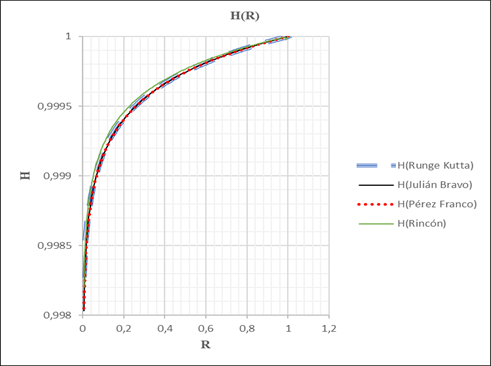
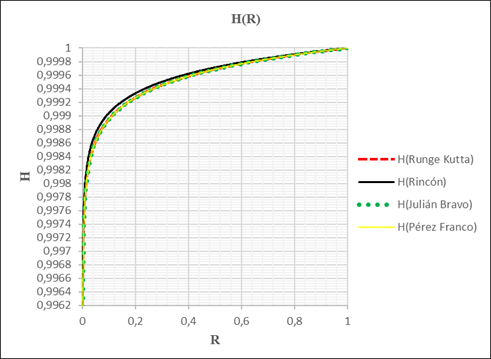
Las figuras 1, 2, 3, 4, 5, 6 y 7 muestran los resultados de las simulaciones realizadas
Resultados y observaciones generales
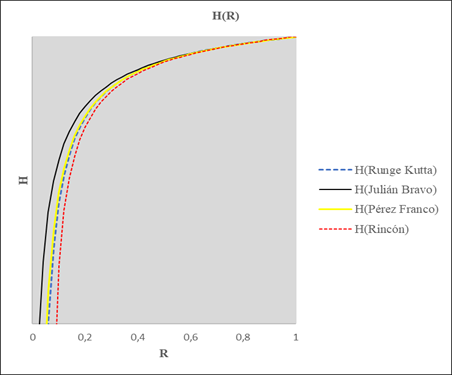
Para empezar, si se realiza un análisis somero a los resultados obtenidos en las figuras 1 y 2, se podría deducir que las expresiones obtenidas por Pérez Franco (7) y Bravo Castillero (8), se alejan de la solución real obtenida por Runge Kutta para h = 50, por consiguiente, se podría concluir que la solución propuesta por el autor (9), obtiene una mejor aproximación a la solución real cuando los valores de ho y ro son pequeños.
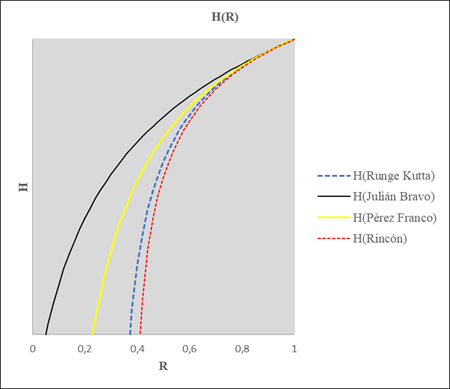
No obstante, realizando un juego riguroso de datos; alguno de ellos expresado en la figura 4 cuando ho y ro son pequeños, se concluyó que la formulación (9) es más precisa que las demás para b ≈ a, condición que en la práctica resultaría improbable o quizás imposible. Además, manteniendo dicha relación anterior y aumentando los valores de ho y ro figura 5, se puede llegar prácticamente al mismo resultado conceptual obtenido en las figuras 3, 6 y 7.
En este orden de ideas, para los resultados obtenidos por la ecuación (9); cuando ho y ro son pequeños, se genera un intervalo en las ordenadas para el cual la función no tendrá una solución real, por tanto, a medida que b se aproxime al valor de a, el intervalo de la función H(R) donde adquiere valores imaginarios se reducirá considerablemente y tenderá a intervalos infinitesimales próximos a cero. De hecho, el caso anterior se observa de la misma manera aun cuando b > a, resultados que se pueden apreciar en las figuras 1 y 2, donde no fue posible conseguir resultados completos debido al intervalo mayor generado que no pertenece a valores reales de la función H(R).
De otro modo, al aumentar en pequeñas proporciones ho y ro, partiendo de ho = 1 y ro = 1, para, b ≈ a, tanto para solución numérica como para las demás expresiones, ambas resultan bastante idénticas, pero cuando ho y ro adquieren valores altos ya no se ajusta la formulación (9) a las expresiones (7 y 8) y; por ende, a la solución numérica (ver figuras 4 y 5).
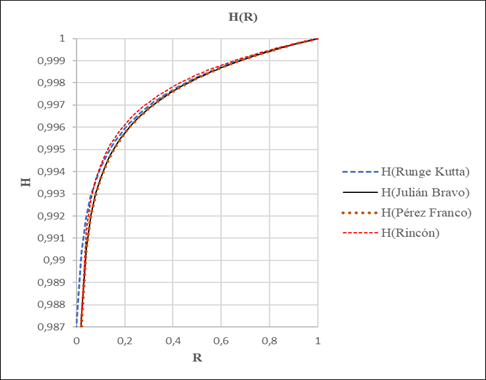
Ahora bien, al establecer valores acordes para a y b (b > a) y valores promedio en relación con las características típicas de los acuíferos libres (ver tabla 1); para realizar las simulaciones 3, 6 y 7 con diferentes valores de paso h(50, 200, 1000) para la solución numérica, se obtuvo los siguientes resultados expresados en las figuras 3, 6 y 7, los cuales guardan bastante similitud. Asimismo, se pudo corroborar teniendo en cuenta las figuras 1, 2 y 4, que la formulación propuesta por Bravo Castillero (1993, 1994) es más precisa a medida que ε sea más pequeño; condición que satisface las condiciones en la realidad, por lo tanto, las ventajas de la aproximación asintótica son indiscutibles debido a la comodidad y precisión de esta.
Por lo tanto, realizando un análisis a los resultados obtenidos y expresados en las figuras anteriormente mencionadas 3, 6 y 7, se puede deducir con facilidad que las expresiones propuestas por Pérez Franco (7) y Bravo Castillero (8) resultan bastante idénticas, corroborando una de las conclusiones a las cuales llegó Bravo Castillero (1993, 1994) en su momento, al comparar los resultados numéricos de ambas ecuaciones obtenidas.
Es importante mencionar; realizando diversos juegos de datos, que la propuesta de Pérez Franco se ajusta mejor a la solución numérica para valores pequeños de ho y ro, por el contrario, para valores relativamente promedio o altos de 𝑟 𝑜 y valores pequeños o altos para ho, las formulaciones obtenidas por Pérez Franco (7) y Bravo Castillero (8) resultan similares. Sin embargo, a pesar de los resultados anteriores ambas formulaciones son similares, conclusión misma a la que llegó Bravo Castillero (1994).
Ahora, en relación con la formulación obtenida por el autor (9), existe una desviación levemente pronunciada que difiere de la solución obtenida por la solución numérica, sin embargo, se ajusta satisfactoriamente como una aproximación menos precisa a las soluciones propuestas por los autores mencionados y, por ende, a la solución real.
Por último, con el fin de identificar la inconsistencia en el intervalo observado en la expresión (9) hacia la solución numérica y las expresiones obtenidas por los autores mencionados, si se examinan las ecuaciones (7) y (9), se puede deducir que:  y
y 
De hecho, se puede identificar con facilidad analizando las figuras 3, 5, 6 y 7 que los factores ω D y ω T tienen mayor incidencia a medida que R se acerca al cero por la izquierda, desviación que es observada sin dificultad en los resultados adquiridos.
Conclusiones
Para empezar, ante las dificultades que presenta para ciertas condiciones específicas la ecuación propuesta con anterioridad por (Rincón, 2022), no se recomienda utilizar la expresión (9), aunque el error cometido para la componente lineal (ω D ) y turbulenta (ω T ) sea progresivo a medida que disminuye R, es decir, que el error máximo será del 2% y 3% respectivamente para R=0.
Por el contrario, ante las diversas ventajas de una aproximación asintótica por su comodidad y precisión, se recomienda utilizar la ecuación propuesta por Bravo Castillero (1993). Por lo demás, no se descarta en ningún momento la formulación obtenida por Pérez Franco (1982), teniendo en cuenta que se obtiene mayor precisión para valores pequeños de ho y ro que la ecuación propuesta por Bravo Castillero, no obstante, ambas ecuaciones se asemejan con bastante precisión a la solución numérica.
Finalmente, resulta necesario modificar la expresión obtenida en un trabajo anterior por Rincón (2022), con el fin de lograr mejores resultados con respecto a lo expuesto en dicho trabajo.