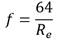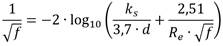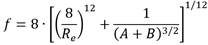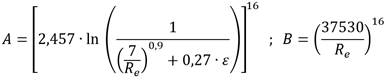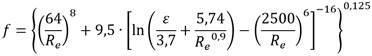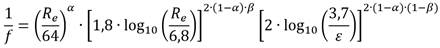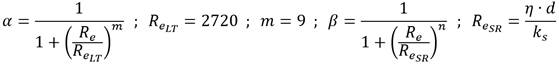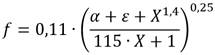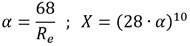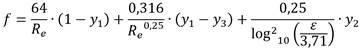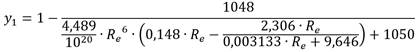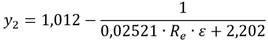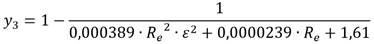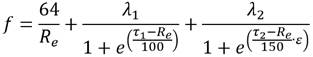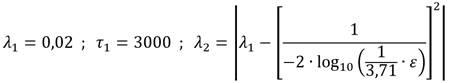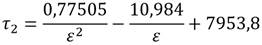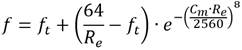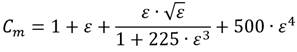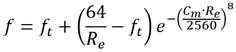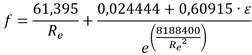Introducción
Para empezar, en el diseño de conducciones para el transporte de fluidos se emplean diferentes ecuaciones para establecer el factor de fricción en régimen laminar y turbulento, pero es posible que existan variaciones importantes de los diferentes parámetros inmersos en el fenómeno físico, que cambien significativamente el régimen de flujo laminar hacia turbulento (flujo hidráulicamente liso o rugoso) o viceversa.
Ahora bien, diversos investigadores han propuesto formulaciones que abarcan todos los regímenes de flujo, sin embargo, se desconoce, sobre todo en las expresiones más vanguardistas, la precisión y, por ende, la confiabilidad de estas.
No obstante, es importante destacar que Díaz-Damacillo et al. (2020) realizó la evaluación, según la expresión de Colebrook-White, de dos ecuaciones en cuestión relativamente modernas; la propuesta de Brkić and Praks (2018) y Díaz-Damacillo and Plascencia (2019). En efecto, los investigadores encontraron que, para algunos valores de ε entre el rango 102 ≤ Re ≤ 109, el error relativo máximo fue 10,02% y 9,83% de forma respectiva.
Por último y, ante cierta incertidumbre en relación con este tipo de formulaciones, en esta investigación se evaluarán las ecuaciones presentadas, por medio del algoritmo CPR hecho por los autores, con el objetivo de establecer la precisión y, por consiguiente, la confiabilidad de los resultados que cada expresión proporciona.
Ecuaciones unificadas para determinar el factor de fricción de Darcy-Weisbach
Antes que todo, no es ocioso recordar que el factor de fricción, en régimen laminar, se deriva de la ecuación de Hagen−Poiseuille y Darcy−Weisbach, por lo tanto, resulta que: (ecuación 1)
Por otro lado y, en un principio diseñada para determinar el factor de fricción en régimen transicional, se tiene la formulación de Colebrook-White (1939): (ecuación 2)
donde:
R e |
número de Reynolds. |
f |
factor de fricción de Darcy−Weisbach. |
k s |
rugosidad absoluta de la tubería. |
d |
diámetro de la tubería. |
Ɛ = k s /d |
rugosidad relativa. |
Por lo demás, cabe mencionar que la expresión (2) probó ser válida para todo tipo de flujo turbulento en tuberías; sin embargo, al ser esta una ecuación implícita para el factor de fricción implica la necesidad de utilizar algún método numérico para calcularlo (Saldarriaga 2016).
Formulación de Churchill
Churchill (1977) desarrolló la siguiente formulación que, según el autor, es válida para todo número de Reynolds R e , y rugosidad relativa Ɛ. (ecuación 3)
donde:
Es importante indicar, que la parte turbulenta de la expresión (3) se basa en la aproximación hecha por Churchill para la ecuación de Colebrook−White (Churchill 1973).
Formulación de Swamee
Swamee (1993) planteó la siguiente expresión:
Ahora bien, cabe resaltar que el autor no define explícitamente el rango de aplicación para la expresión (4), sin embargo, el autor evalúa la ecuación anterior en los intervalos dados por el diagrama de Moody (1944), por consiguiente, se puede deducir que dicha formulación es válida para todo el rango del diagrama mencionado.
Por lo demás, no es ocioso señalar que la expresión (4) considera la aproximación de Swamee y Jain (1976) para la ecuación de Colebrook−White.
Formulación de Cheng
Cheng (2008) estableció la siguiente ecuación:
donde:
Es relevante anotar, que la expresión anterior sigue los resultados obtenidos por el experimento de Nikuradse (1950).
Formulación práctica de la ingeniería rusa
A. Chernikin y B. Chernikin (2012), desarrollaron la siguiente formulación:
donde:
Ahora, cabe aclarar que la parte turbulenta de la formulación (6) se basa en una expresión hecha en 1982 por un investigador ruso, de hecho, dicha ecuación se usa comúnmente en Rusia en lugar de la formulación de Colebrook−White, cuando se diseñan y operan redes para el transporte de petróleo crudo (A. Chernikin and B. Chernikin 2012).
Por último y, con respecto a la incertidumbre del rango de aplicación para la expresión (6), Brkić and Praks (2018) corroboraron que, para valores pequeños de rugosidad relativa entre, 103,7 ≤ R e ≤ 105,8,las ecuaciones (2 y 6) producen resultados casi idénticos, no obstante, a medida que el valor de la rugosidad relativa aumenta el resultado obtenido por la formulación (6) se aleja del adquirido por Colebrook−White (expresión 2), situación que, según Brkić and Praks (2018), es cuestionable.
Formulación de Brkić y Praks
Brkić and Praks (2018), propusieron la siguiente ecuación que, infiriendo por sus resultados obtenidos, es válida para todo el rango del diagrama de Moody (1944). (ecuación 7)
donde:
Para acabar, cabe subrayar que la formulación (7) considera el comportamiento flexional de Nikuradse (1950).
Formulación de Díaz−Damacillo y Plascencia
Díaz−Damacillo and Plascencia (2019), plantearon una expresión que, un tiempo más tarde, fue modificada por Díaz−Damacillo et al. (2020). La formulación actualizada que, según los autores es aplicable para una amplia gama de valores de R e y Ɛ (Díaz−Damacillo et al. 2020), viene dada por: (ecuación 8)
donde:
Por lo demás, cabe resaltar que la ecuación (8) sigue la conducta flexional de Nikuradse (1950).
Formulación de Avci y Karagoz
Avci y Karagoz (2019), desarrollaron la siguiente formulación que, infiriendo por sus resultados adquiridos, es válida para todo el rango del gráfico de Moody (1944). (ecuación 9)
donde:
Ahora bien, es significativo señalar que la función f t hace referencia al factor de fricción calculado en régimen turbulento, por ende y, según el trabajo realizado por Avci y Karagoz (2009), dicho factor resulta que:
Para terminar, es crucial anotar que la expresión (9) prosigue el comportamiento monotónico de Colebrook−White.
Variante para la formulación de Avci y Karagoz
Milošević et al. (2022), introdujeron la ecuación que recomienda Brkić and Praks (2020) para el factor de fricción en régimen turbulento f t , que se encuentra inmerso en la función general obtenida por Avci y Karagoz (2019). En este orden de ideas, la formulación resultante es la siguiente.
donde:
Para finalizar, es notable aludir que la función f t puede ser cualquier propuesta coherente que se haya realizado a través del tiempo.
Formulación de Milošević, Brkić, Praks, Litričin y Stajić
Milošević et al. (2022), reportan la siguiente formulación que fue desarrollada mediante regresión simbólica. (ecuación 11)
Ahora bien, es fundamental indicar que la expresión (11) fue evaluada para una rugosidad relativa de 0,05 entre el rango 0 ≤ R e ≤ 103,78, obteniendo resultados similares a los conseguidos por la (ecuación 7).
En suma, cabe acentuar que la formulación (11) sigue la conducta flexional de Nikuradse (1950), aunado a ello, es relevante señalar que, según el conocimiento actual de los autores, la expresión (11), de acuerdo con la temática correspondiente, es la más contemporánea.
Algoritmo CPR
Para iniciar, el algoritmo CPR, desarrollado por los autores, es una herramienta programada en el lenguaje Python (versión 3.11 o 3.12), cuyo objetivo es evaluar los resultados obtenidos por las ecuaciones aproximadas, en relación con las formulaciones (1 y 2). En este orden de ideas, los autores disponen a los interesados el algoritmo en un repositorio de GitHub (https://github.com/BlutLucifugeKrieger/CPR-Algorithm), con el fin de satisfacer cualquier tipo de exigencia académica u ocupacional.
Por lo demás, a continuación, dejando un poco de lado la programación a fondo del CPR, se resumen las características más importantes en las cuales se basa este; sin embargo, si el lector desea profundizar en la programación o realizar algún cambio se recomienda clonar el algoritmo que se encuentra en el repositorio mencionado.
Rango evaluado para el número de Reynolds y la rugosidad relativa
Las condiciones adoptadas para el régimen laminar, transicional y turbulento se establecieron en R e ≤ 2000, 2000 < R e < 4000, y R e ≥ 4000 respectivamente (Moody 1944), por ende, el intervalo evaluado para 𝑅 𝑒 , en flujo laminar y turbulento, fue 10-10 ≤ R e ≤ 2000 y 4000 ≤ R e ≤ 108 correlativamente, por otra parte, el rango evaluado para la rugosidad relativa fue 10-10 ≤ Ɛ ≤ 0,05-10; no obstante, el usuario podrá seleccionar el rango que desee en el CPR, aunque los autores recomiendan que el límite inferior no sea igual a cero, ya que dicho punto es problemático.
Distribución de la muestra (puntos cuasi aleatorios de Sobol)
El método de Sobol cuasi−Monte Carlo llena el espacio de posibilidades de manera más uniforme en el rango de una muestra, por ende, los números de Sobol generados ofrecen una menor discrepancia entre sí, lo cual hace que se obtengan puntos que abarquen eficientemente el intervalo de una muestra (Brkić and Praks 2022).
En este sentido, las secuencias de Sobol proporcionan n=2 m puntos en el intervalo (0,1) d , donde d es la dimensionalidad de la secuencia. Por otro lado, es importante resaltar que Brkić and Praks (2022) concluyeron que, con m=6, es suficiente para obtener resultados aceptables sin necesidad de evaluar las infinitas posibilidades.
Por lo anterior, para el desarrollo específico de este trabajo los autores eligieron un m=10, es decir, 1024 puntos para el intervalo del número de Reynolds y la rugosidad relativa, de hecho, el índice total de los vectores resultantes, conforme a la cantidad de puntos de R e y Ɛ, es 10242. No obstante, el usuario puede seleccionar un valor diferente para m, según las necesidades que este requiera, pero sin que m sea mayor que trece, ya que para valores más grandes se debe disponer de un equipo de gran capacidad computacional y, aunado a ello, se tendrá que modificar un parámetro denominado “bits”, que hace parte del instrumento que se describe próximamente.
Ahora bien, el método mencionado es un procedimiento complejo que requiere una herramienta computacional. En este orden de ideas, en Python existe un motor denominado Sobol, que hace parte del sub-módulo cuasi−Monte Carlo de la librería SciPy de código abierto, por lo tanto, los autores implementaron dicho motor en este trabajo.
En otro sentido, cabe destacar que actualmente en el motor Sobol existen dos métodos de optimización para mejorar la calidad de la muestra; “random-cd” y “lloyd”, por ende, los autores utilizaron ambas metodologías, no obstante, el usuario definirá si desea o no implementar algún método mencionado.
Para terminar, si el lector requiere saber cómo usar el motor de Sobol o conocer más sobre este se recomienda acceder a la documentación de dicho sub-módulo (The SciPy Community 2023).
Desarrollo de la ecuación de Colebrook−White
El método numérico utilizado por los autores para solucionar la ecuación de Colebrook−White fue el de Newton−Raphson, el cual, por lo general, sólo requiere tres iteraciones para que el método converja (Saldarriaga 2016), de hecho, Brkić (2011) afirma que normalmente se necesita menos de siete iteraciones.
En este sentido y, para el desarrollo de este trabajo, los autores eligieron siete iteraciones para el método mencionado.
Cuantificación del error relativo
Para comenzar, es importante señalar que los valores obtenidos para el error relativo se programaron en cada régimen de flujo (laminar y turbulento), es decir, se caracterizó ambas zonas, con el fin de identificar exclusivamente el error en el régimen dado.
Por lo anterior, las fórmulas programadas para cuantificar el error mencionado son las siguientes:
donde:
L RE |
error relativo mínimo, promedio o máximo en régimen laminar. |
T RE |
error relativo mínimo, promedio o máximo en régimen turbulento. |
Finalmente, es indispensable aclarar que el error relativo promedio no es obtenido por el promedio entre el error relativo mínimo y máximo, sino que dicho error se adquiere como el promedio de toda la cantidad de datos que pueden existir en el vector del error relativo, siguiendo el régimen de flujo correspondiente.
Resultados
Antes que nada, es pertinente resaltar que en los siguientes resultados se obtuvo un mayor número de decimales, pero, por practicidad, los autores sólo consideraron tres decimales truncados para cada uno de ellos.
A continuación, se presentan las tablas (1, 2 y 3), donde se exponen los resultados adquiridos por el algoritmo CPR para cada modelo, de hecho, se resaltan las formulaciones con mejores resultados.
Tabla 1 Error relativo de las ecuaciones evaluadas para régimen laminar y turbulento (muestreo tipo Sobol)
| Autor y ecuación | Régimen de flujo | |||||
|---|---|---|---|---|---|---|
| Laminar | Turbulento | |||||
| L
|
L
|
L
|
T
|
T
|
T
|
|
| Churchill (3) | 0,000 | 0,003 | 0,131 | 4,543E-07 | 0,058 | 3,103 |
| Swamee (4) | 0,000 | 0,005 | 0,598 | 1,919E-08 | 0,033 | 1,401 |
| Cheng (5) | 0,000 | 0,242 | 2,909 | 3,243E-04 | 0,064 | 40,534 |
| A. Chernikin y B. Chernikin (6) | 5,589E-07 | 0,196 | 3,457 | 3,575E-04 | 16,217 | 46,818 |
| Brkić y Praks (7) | 5,852E-06 | 14,057 | 58,378 | 1,192E-04 | 1,169 | 86,337 |
| Díaz−Damacillo et al. (8) | 0,000 | 8,956 | 25,276 | 2,074E-06 | 1,160 | 236,639 |
| Avci y Karagoz (9) | 0,000 | 1,628 | 30,425 | 2,765E-05 | 0,967 | 3,106 |
| Brkić y Praks (10) | 0,000 | 1,745 | 31,435 | 1,175E-04 | 0,103 | 0,124 |
| Marko Milošević et al. (11) | 3,060E-05 | 3,986 | 17,958 | 1,302E-03 | 22,890 | 311,438 |
Tabla 2 Error relativo de las ecuaciones evaluadas para régimen laminar y turbulento (muestreo tipo Sobol−optimización por “random-cd”)
| Autor y ecuación | Régimen de flujo | |||||
|---|---|---|---|---|---|---|
| Laminar | Turbulento | |||||
| L
|
L
|
L
|
T
|
T
|
T
|
|
| Churchill (3) | 0,000 | 0,003 | 0,131 | 4,543E-07 | 0,058 | 3,103 |
| Swamee (4) | 0,000 | 0,005 | 0,598 | 1,919E-08 | 0,033 | 1,401 |
| Cheng (5) | 0,000 | 0,242 | 2,909 | 3,243E-04 | 0,064 | 40,534 |
| A. Chernikin y B. Chernikin (6) | 5,589E-07 | 0,196 | 3,457 | 3,575E-04 | 16,217 | 46,818 |
| Brkić y Praks (7) | 5,852E-06 | 14,057 | 58,378 | 1,192E-04 | 1,169 | 86,337 |
| Díaz−Damacillo et al. (8) | 0,000 | 8,956 | 25,276 | 2,074E-06 | 1,160 | 236,639 |
| Avci y Karagoz (9) | 0,000 | 1,628 | 30,425 | 2,765E-05 | 0,967 | 3,106 |
| Brkić y Praks (10) | 0,000 | 1,745 | 31,435 | 1,175E-04 | 0,103 | 0,124 |
| Marko Milošević et al. (11) | 3,060E-05 | 3,986 | 17,958 | 1,302E-03 | 22,890 | 311,438 |
Tabla 3 Error relativo de las ecuaciones evaluadas para régimen laminar y turbulento (muestreo tipo Sobol−optimización por “lloyd”)
| Autor y ecuación | Régimen de flujo | |||||
|---|---|---|---|---|---|---|
| Laminar | Turbulento | |||||
| L
|
L
|
L
|
T
|
T
|
T
|
|
| Churchill (3) | 0,000 | 0,004 | 0,131 | 4,092E-07 | 0,059 | 3,103 |
| Swamee (4) | 0,000 | 0,006 | 0,598 | 5,945E-07 | 0,035 | 1,401 |
| Cheng (5) | 0,000 | 0,248 | 2,909 | 3,243E-04 | 0,083 | 40,534 |
| A. Chernikin y B. Chernikin (6) | 1,434E-06 | 0,203 | 3,457 | 1,193E-03 | 16,255 | 46,818 |
| Brkić y Praks (7) | 6,980E-06 | 14,099 | 58,378 | 1,270E-04 | 1,178 | 86,337 |
| Díaz−Damacillo et al. (8) | 0,000 | 8,958 | 25,276 | 8,154E-06 | 1,535 | 236,639 |
| Avci y Karagoz (9) | 0,000 | 1,663 | 30,425 | 7,522E-05 | 0,963 | 3,106 |
| Brkić y Praks (10) | 0,000 | 1,782 | 31,435 | 1,175E-04 | 0,103 | 0,124 |
| Marko Milošević et al. (11) | 5,088E-06 | 4,007 | 17,958 | 6,542E-02 | 23,272 | 311,438 |
Por último, las muestras generadas por el motor Sobol, tanto para R e y Ɛ, fueron las mismas en cada evaluación; sin embargo, si el usuario desea que en cada ejecución del CPR las muestras cambien, deberá insertar su decisión en el input, cuando el algoritmo se lo requiera. En todo caso, se recomienda consultar la documentación asociada para más información.
Conclusiones
Para comenzar, es importante destacar que las ecuaciones presentadas siguen el comportamiento monotónico de Colebrook-White o el flexional de Nikuradse. Por lo tanto, resulta claro que las expresiones basadas en los resultados de Nikuradse sean las de menor precisión, puesto que la evaluación se realizó con respecto a la formulación universalmente aceptada; la ecuación de Colebrook-White.
En este orden de ideas, es notable enfatizar que los resultados obtenidos son equivalentes, de hecho, el resultado del muestreo general de Sobol (tabla 1) con el logrado por el método de optimización “random-cd” (tabla 2), son idénticos, aunque en realidad, esta casualidad se debe al recorte realizado de los decimales inmersos en cada resultado.
Por otro lado, los autores establecieron que, según el muestreo de puntos cuasi aleatorios de Sobol alcanzados por el CPR, las ecuaciones con menor error relativo máximo, para régimen laminar y turbulento, son las propuestas de Churchill (1977) y Brkić and Praks (2020) [expresión dada en Milošević et al. (2022)] respectivamente.
No obstante, los autores concluyen que, teniendo en cuenta los resultados obtenidos para el error relativo promedio en ambos regímenes de flujo, la formulación de Swamee (1993) es la más adecuada, aunque no se descarta la expresión de Churchill (1977), ya que la diferencia del error cometido en cuestión por ambas ecuaciones, para flujo laminar y turbulento, no es muy contundente.
En otro sentido, es posible realizar diferentes pruebas adicionales con el algoritmo CPR, ya que este cuenta con la practicidad de validar eficazmente diversas condiciones para las funciones presentadas en este trabajo, en cualquier caso y, para casos extraordinarios, se recomienda consultar previamente la documentación del motor Sobol.
En suma, los autores consideran que, conforme a los resultados presentados y de acuerdo con los requerimientos específicos para cada caso, el lector determine qué ecuación le resulta más conveniente utilizar.