Introducción
La protección de distancia es ampliamente utilizada para la protección de las redes de trasmisión y debería ser utilizada como protección de respaldo y no como protección principal [1], pero algunos ingenieros no conocen las causas de porqué hay que asignarle este papel de respaldo en la protección de las líneas. La protección de distancia, función de protección (21 código ANSI), es una protección direccional por naturaleza, con selectividad relativa que tiene como órgano de medición un relé de impedancia, que opera contra los cortocircuitos en la línea que protege. Dicha protección determina la razón entre la tensión y la corriente (impedancia) de la línea en donde se encuentra conectada, que en condiciones de falla trifásica metálica no es más que la distancia entre el punto de conexión y el fallo.
Las protecciones de distancia no siempre aseguran una aceptable selectividad para cortocircuitos internos para su primer y segundo escalón en la mayoría de las configuraciones actuales [2].Las protecciones de distancia no siempre aseguran una aceptable selectividad para cortocircuitos internos para su primer y segundo escalón en la mayoría de las configuraciones actuales [2]. Para la protección de líneas se emplean fundamentalmente tres escalones de la protección de distancia. El primer escalón se ajusta con una impedancia alrededor de 80% de la impedancia de línea que se está protegiendo. El segundo escalón se ajusta de tal forma que asegure la protección total de la línea y el tercer escalón, se ajusta para que detecte fallas en la línea o el elemento que esté conectado aguas abajo.
Estas condiciones de pre-falla están relacionadas con [3-4].
La resistencia involucrada en la falla
La cantidad y dirección de la transferencia de potencias por la línea antes de la falla o en condiciones de pre-falla
Las potencias de cortocircuitos de las fuentes en ambos extremos de la línea
La protección de distancia se puede realizar con varias formas o zonas de protección, teniendo en cuenta la longitud de la línea, la tensión de alimentación, la característica en el plano complejo del relé, la tendencia a producirse cortocircuitos con resistencias de arco y las oscilaciones de potencia del sistema. Entre estas formas se pueden encontrar relés tipo impedancia, relés tipo MHO, relés con característica cuadrilateral, y otros.
En ocasiones no se toman en cuenta las condiciones de pre-falla a la hora de realizar los ajustes de los escalones de las protecciones de distancia, además de utilizarla en configuraciones donde es poco confiable. En este trabajo se analiza utilizando la simulación matemática, como influyen de forma negativa las condiciones de pre-falla en la operación de los relés de distancias empleados en las líneas de trasmisión cuando existen arcos eléctricos caracterizados por su resistencia.
Materiales y métodos
Es importante que el comportamiento de las protecciones en los Sistemas Eléctricos de Potencia (SEP), sea sumamente confiable, debido al elevado valor de los elementos que protegen y que las protecciones constituyen la primera barrera para lograr la estabilidad del sistema frente a grandes perturbaciones. Si las protecciones separan los elementos en cortocircuito de forma rápida, el sistema tendrá más posibilidades de lograr la estabilidad luego de la avería [2-5]. La protección de distancia es ampliamente utilizada en nuestro país en redes eléctricas con tensiones iguales y superiores a 110kV. Esta protección puede realizar operaciones incorrectas por numerosos factores: efecto de las fuentes intermedias, condiciones de prefalla, oscilaciones de potencia, efecto de la carga y acoplamiento mutuo. El relé de distancia tipo Mho [1-6], es ampliamente utilizado, aunque en la actualidad en la mayoría de los SEP se utiliza el rele de distancia tipo cuadrilateral.
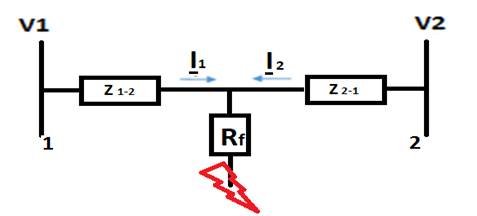
Las condiciones de prefalla se presentan de manera negativa en la operación de la protección de distancia, ya que se afectan los valores de medición de la impedancia. En la figura 1, se observa un esquema simplificado de una línea simple circuito, considerando que el cortocircuito tiene resistencia de arco Rf. Este esquema servirá de base para el análisis del efecto de la pre-falla en la impedancia que mide un relé de distancia.
Para una protección de distancia ubicada en el extremo de la línea más cercano a la barra 1 (Fig. 1), para una falla trifásica, este mediría una tensión V1 en función de la ecuación (1).
Donde:
V1 |
tensión en el extremo de medición |
I1 |
corriente en el extremo de medición |
I2 |
corriente en el otro extremo lejano de la línea fallada |
Rf |
resistencia involucrada en la falla |
Luego para calcular la impedancia involucrada en la falla se tiene la ecuación (2):
Simplificando la ecuación se obtiene la ecuación (3):
Como se observa en la ecuación (3), el valor de la impedancia de falla medida por el relé de distancia no va a depender solo de la impedancia involucrada en la línea fallada, ni de la resistencia involucrada en la falla (Rf), sino también de las corrientes por ambos extremos de la línea.
La impedancia medida por el relé depende de la relación entre I2 y I1 siempre que exista resistencia de falla, por lo que se presenta como una dificultad real ya que en los cortocircuitos casi siempre habrá Rf, en gran parte aportada por el arco eléctrico.
Como la impedancia medida, cuando existe resistencia de falla, va a depender de la intensidad de las corrientes tanto de las que pasan por el punto de medición, como las corrientes del otro extremo de la línea y sus desfasajes, entonces la magnitud y el ángulo de dichas corrientes afectarán la medición de la impedancia. La magnitud de las corrientes estará sujeto a las capacidades de cortocircuitos de las fuentes en ambos extremos de la línea y sus ángulos al estado de la trasferencia antes de ocurrir la falla (condiciones de prefalla).
Resultados y discusión
En el sistema eléctrico simplificado mostrado en la figura 2, se simularán cortocircuitos trifásicos en la línea que une las barras 2 y 3 y se analizarán los valores de las mediciones de impedancia del relé de distancia tomando en cuenta la resistencia involucrada en el cortocircuito y la transferencia que existía antes de la falla.
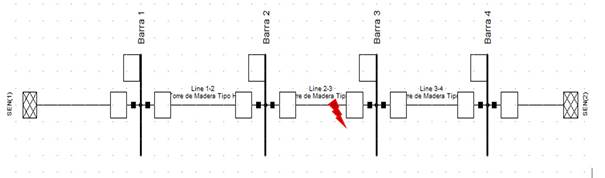
Fig. 2 Sistema de transmisión con líneas tipo torre de 110 kV, montado en el software matemático PowerFactory DigSilent 15.1.7.
En este sistema simplificado que se muestra en la figura 2, las líneas tienen la misma impedancia 0,218Ω+j3,038Ω y tienen a su vez, la misma distancia de 10 km. Los sistemas equivalentes instalados en ambos extremos tiene 1500 MVA de cortocircuitos. Esta red opera en 110kV así que es una típica red simple circuito de trasmisión que une dos áreas de generación.
Efecto de la resistencia de falla
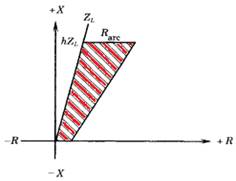
La impedancia de una línea de la transmisión típica es muy inductiva. Esto significa que la impedancia que mide el relé, en un plano complejo X-R, quedará sobre la impedancia de la línea [2-3].
Se pensaría que el efecto de la resistencia del arco, mueve la impedancia en plano X-R sacándola de la característica donde está ubicada la impedancia de la línea como se observa en la figura 3.
En la línea 2-3 mostrada en la figura 2, se simula un cortocircuito al 50 % de la longitud de la línea y se variarán los valores de la resistencia de falla mostrados en la tabla 1. Nótese que aunque la falla no se ha movido de posición la impedancia medida por el relé es distinta para cada valor de resistencia de falla.
Tabla 1 Valores de impedancia medidas por el relé para un cortocircuito en el 50% de la línea, con distintos valores de resistencia de falla
| Impedancia de Falla (Ω) | |
|---|---|
| 0 | 0,1094 + j1,5231 |
| 0.4 | 0,9000 + j1,5180 |
| 0.6 | 1,3090 + j1,5190 |
| 0.8 | 1,7090 + j1,5190 |
| 1 | 2,1014 + j1,5139 |
| 1,2 | 2,5065 + j1,5170 |
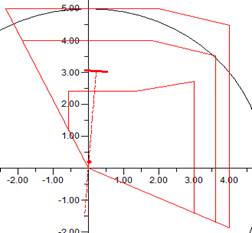
En la figura 4, se muestra las zonas de operación del relé analizado que es el que está conectado al extremo más cercano a la barra 2 (fig. 2), considerando que es un relé tipo MHO con tres zonas de operación calculadas aproximadamente para dicha línea, y considerando los valores de resistencia de falla mostrados en la tabla 1.
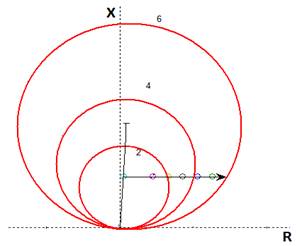
Fig. 4 Ubicación del CC en las zonas de operación del relé de distanica ubicado en la barra 1 con una resitencia de falla de 0 hasta 1,2 Ohm en el sentido de la saeta.
Para un valor aproximado de 0,8 ohm de resistencia de falla, la medición de la impedancia ya se encuentra operando incorrectamente al salirse de primera zona de operación si se utiliza un relé de distancia tipo MHO, y con el aumento de la resistencia de falla la impedancia pasa a ser vista por la zona 2 y hasta llega a ser visto solo por la zona 3 para valores más altos de resistencia de falla.
El problema que introduce el incremento que pueda tener la resistencia de falla, se intenta resolver instalando un relé de distancia con característica cuadrilateral en lugar de uno Mho [4-7], representado en la figura 5. Con la característica cuadrilateral se reduce la contradicción existente entre el efecto de la resistencia de arco sobre la no operación del relé (que demanda una característica ancha de acuerdo al eje R) [2-6].
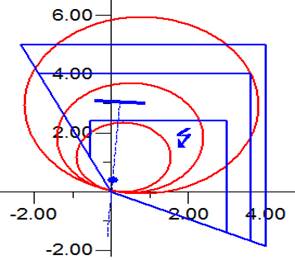
Fig. 5 Ubicación del CC en las zonas de operación del relé de distancia tipo Mho y cuadrilateral con una resistencia de falla de 0,8 Ohm.
En la figura 5, se observa que la falla quedará en la primera zona de operación del relé cuadrilateral lo que es correcto, mientras que a su vez la falla queda fuera de la primera zona de operación del relé tipo Mho lo que no es correcto.
Se pudiera decir que la solución del problema de selectividad de la los relés de distancia debido a la resistencia involucrada en la falla, es emplear en las líneas aéreas de trasmisión relés Cuadrilaterales en lugar de relés tipo MHO, pero a continuación se constatará que esta solución no es totalmente efectiva.
Efecto de la cantidad y dirección de la transferencia de potencias por la línea
Considérese que el sistema de la figura 2, no tiene transferencia entre las fuentes y se simulará una falla trifásica en un punto al 50 % de la longitud de la línea 2-3. A continuación se puede observar que pasa con el ángulo de la corriente de cortocircuito en las barras a las que se encuentra conectada la línea fallada.
Medición en la Barra 2: -88,653 °
Medición en la Barra 3: -88,033 °
Se observa que la diferencia entre los ángulos de la medición de cada barra es mínima, menor que 1%, por lo que no es significativo. Es decir, si no hay transferencia no hay diferencia angular entre las fuentes conectadas a ambos extremos de la línea. Esta no es una situación normal, lo normal es que por las líneas existan transferencias.
Ahora se tendrá una transferencia del Sistema 1 hacia el Sistema 2, lo que significa un envió de 120 MW, y se simulará una falla al 50 % de la línea 2-3. La diferencia entre los ángulo de las corrientes que ingresan a la línea es de un 43 % y esto es debido a la transferencia de potencia activa que existía antes de la falla que era de 120 MW.
Medición en la Barra 2: -57.245 °
Medición en la Barra 3: -99.424 °
La transferencia de potencia activa que existía antes de la falla influye de manera importante en la diferencia angular de las corrientes proveniente de ambas fuentes. Esta diferencia angular está relacionada con el ángulo de la fem antes de que ocurra la falla y es por eso que este ángulo corresponde a las condiciones de prefalla. Tomando como base la ecuación (3), se observa el valor de la impedancia de falla no va a depender solo de Rf, sino también a la relación fasorial entre las corrientes por ambos extremos de la línea. La impedancia medida depende del factor entre I2 e I1. Como la impedancia medida, cuando existe resistencia de falla, va a depender de los fasores de las corrientes tanto los que pasan por el punto de medición, como las corrientes del otro extremo de la línea, entonces la magnitud y el ángulo de dichas corrientes afectarán la medición de la impedancia. Con anterioridad se evidenció que cuando la transferencia por la línea era cero, la diferencia angular entre las corrientes era pequeña es decir I2/I1 será prácticamente uno si las fuentes son iguales, ahora bien cuando existe una transferencia se tendrá que este coeficiente I2/I1 introducirá un comportamiento angular, ya que existe una diferencia en estos valores. Dependiendo del sentido en el que se encuentre la transferencia por las líneas, para un mismo cortocircuito en un punto a la mitad de la línea 2-3 para valores de resistencia de falla en aumento el comportamiento será el descrito por los valores de la tabla 2 y 3. Se simula de la misma forma que el experimento anterior una falla al 50 % de la línea 2-3, pero en este caso con transferencia de potencia por la misma enviando del Sistema 1 a Sistema 2, 120 MW previo a la falla y luego con dirección contraria. Los valores medidos por el relé en ambos experimentos se pueden observar en la tabla 2.
Tabla 2 Valores de impedancia medido por el relé para distintos valores de resistencia de falla considerando las condiciones de pre-falla con diferentes direcciones de la transferencia.
| Rf (Ω) |
Impedania (Ω) para 120 MW Desde el Sistema 1 al Sistema 2 |
Impedancia (Ω) para 120 MW Desde el Sistema 2 al Sistema 1 |
|---|---|---|
| 0.4 | 0,754 + j1,2173 | 0,767 + j1,8390 |
| 0.6 | 1,100 + j1,0770 | 1,100 + j2,0200 |
| 0.8 | 1,398 + j0,9440 | 1,450 + j2,1900 |
| 1 | 1,665 + j0,8180 | 1,790 + j2,3800 |
| 1.2 | 1,955 + j0,6990 | 2,160 + j2,6018 |
Ahora se puede notar si se comparan los resultados de la tabla 2, con los obtenidos en la tabla 1, que los resultados de las impedancias que mediría el relé para diferentes valores de resistencia de falla son diferentes con y sin transferencia y en dependencia del sentido que tenga dicha transferencia. Para 0,8 OHM sin transferencia antes de la falla el relé mediría 1,709Ω+j1,519Ω, pero con transferencia de 120 MW desde el sistema 1 al 2 el mismo relé con una falla en la misma posición mediría 1,398Ω+j0,9440Ω y si la transferencia se invierte el relé mediría 1,450Ω +j2,190Ω. Siendo la falla en el mismo punto al 50% de la línea, el relé mide valores diferentes de impedancia cada vez. Este resultado mostrado en las tablas 1 y 2, quiere decir, como se supondría del análisis de la ecuación 3, que la impedancia que mide el relé va a depender no solo si existe resistencia de falla, ni de su valor sino también del estado de transferencia que existía antes de ocurrir la falla. Nótese en la tabla 2, que para una resistencia de falla de 0.8 ohm la impedancia medida por el relé cambia no solo la componente resistiva sino también la componente reactiva inductiva de la impedancia, por tanto el punto de falla se mueve ya no de forma lineal como en el caso de la figura 4, sino de manera transversal. El resultado de la tabla 2, se lleva al plano X-R mostrado en la figura 6.
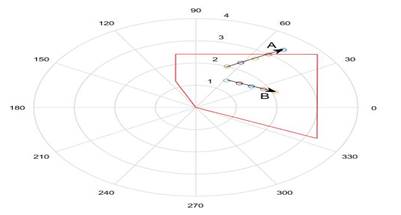
Fig. 6 Ubicación en el plano X-R de la falla para valores de resistencia de arco, A-con trasferencia previa desde SEN 2 a SEN 1(Valores Tabla 2), B-con trasferencia de Sistema 1 a Sistema 2 (Valores Tabla 2).
Se observa que en ambos casos A y B la característica describe un comportamiento lineal pero no paralelo al eje de las resistencias, con el aumento de Rf, lo que se corrobora lo plasmado anteriormente. Los ángulos de las corrientes implicadas en la falla tienen valores diferentes y el factor I2/I1 introducirá un nuevo problema a las mediciones del relé de distancia. Con esto la falla puede quedar fuera de la zona de operación para valores más pequeños de resistencia de falla y la confiabilidad sería aún menor, por ejemplo para un valor de Rf=0,8 Ohm describiendo el comportamiento A de la figura 6, ya la operación no es confiable por su cercanía a la frontera de la zona 1 de operación, y para valores superiores ya estaría fuera de la zona 1 de operación siendo esto incorrecto [4-7-8].
En la figura 6, se observó que el relé cuadrilateral en un primer momento suprime los problemas de la resistencia de falla, pero aún es una problemática el estado de la transferencia antes del cortocircuito, así como las capacidades de cc de las fuentes, ya que estos introducen un comportamiento angular, lo que provocaría disparos incorrectos aún más rápido. Para dar solución a este inconveniente algunos relés tienen una opción que permite realizar una pendiente positiva a la primera zona de operación (TILT) [4-9] como se muestra en la figura 7.
Esta opción del TILT elimina las dificultades de la protección ante las condiciones descritas anteriormente, esencialmente las dificultades que presenta el comportamiento A, mostrado en la figura 6, pero se demostrará que aparecen otros problemas.
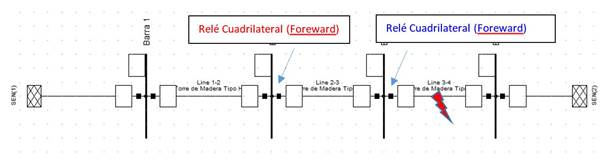
Si se simula una falla en la línea 3-4 al 50 % de su longitud (fig. 8) y se observan las zonas de operación de ambos relés se notará una nueva problemática.
Cuando se muestran en el mismo gráfico las zonas de operación Cuadrilateral de dos relés de dos líneas que están una a continuación de la otra se observa como se muestra en la figura 9. Se observa que al dar pendiente positiva (TILT) garantiza operaciones correctas para la zona 1 de operación del relé ante los comportamientos antes analizados. También se observa que se introduce un área en la zona 1 del relé de la línea siguiente donde se solaparía la operación y para una misma falla pueden operar ambos relés lo que no es correcto [9-10].
Es decir, la solución del TILT puede resolver el problema de que por la transferencia antes de la avería la zona 1 no vea una falla, pero entonces aparecería otro problema de selectividad porque dos protecciones Zona 1 podrían ver la misma falla y ambas desconectarían ambas líneas.
Efecto de las potencias de cortocircuitos de las fuentes en ambos extremos de la línea
El efecto de las potencias de cortocircuito se ve reflejado esencialmente en el módulo de la corriente de falla sin afectar prácticamente el ángulo de la misma. Un aumento de la potencia de cortocircuito se traduce en un mayor aporte a la corriente de falla y viceversa. Cuando las potencias de cortocircuito son iguales las corrientes por cada extremo de la línea fallada lo serán también y el error será solo el doble de la resistencia de falla.
En los sistemas eléctricos de potencia en las líneas de trasmisión es difícil prever los niveles de cortocircuito por cada extremo, ya que estas líneas llevan el peso de la generación que varía en la medida de las necesidades del sistema.
Cuando las potencias de cortocircuito por cada extremo de la línea son diferentes, los errores que introducen la resistencia de falla y la transferencia por las líneas antes de la falla pueden ser mayores o menores en dependencia de la magnitud de las corrientes por cada extremo.
Si por el extremo donde se realiza la medición pasa el mayor aporte de la corriente de la falla (I1˃I2), el error que introduce la diferencia de I2 y I1 en la medición va a ser menor que cuando los aportes son iguales (ver ecuación (3) y tabla 3) ,siendo esta una condición favorable. Pero cuando el aporte de corriente que pasa por el punto de medición es menor que el aporte que viene del otro extremo (I2˃I1) el error será mayor (ver Tabla 3). Un mayor error en las mediciones conlleva a que para valores más pequeños de resistencia de falla y menos trasferencia por las líneas, las consecuencias de estos errores serán peor para la correcta operación del relé de distancia.
Tabla 3 Valores de impedancia medida por el relé para diferentes escenarios (Las corrientes en los casos que no son iguales, la mayor corriente es dos veces el valor de la inferior).
| I1=I2 | I1˃I2 | I2˃I1 | |
|---|---|---|---|
| Rf (Ω) | Impedancia de Falla (Ω) | Impedancia de Falla (Ω) | Impedancia de Falla (Ω) |
| 0 | 0,1094 + j1,5231 | 0,1095+j1,520 | 0,1091+1,519 |
| 0.4 | 0,9000 + j1,5180 | 0,682+j1,517 | 1,431+j1,529 |
| 0.6 | 1,3090 + j1,5190 | 0,96+j1,516 | 2,09+j1,534 |
| 0.8 | 1,7090 + j1,5190 | 1,255+j1,515 | 2,753+j1,540 |
| 1 | 2,1014 + j1,5139 | 1,542+j1,514 | 3,414+j1,545 |
| 1,2 | 2,5065 + j1,5170 | 1,829+j1,513 | 4,07+j1,550 |
Conclusiones y recomendaciones
Cuando se analizan todos los resultados que arrojan los modelos se concluye lo siguiente:
Durante fallas en las redes de trasmisión aéreas, ya sean a tierra o de fase a fase, si existe impedancia de falla el relé de distancia medirá la localización o distancia de la falla de manera incorrecta.
Las posibles soluciones a los problemas introducidos por la resistencia de falla y el aumento o disminuciones de transferencia, sustituyendo un relé tipo MHO por un relé con característica cuadrilateral no son efectivas a 100 %.
Los errores de medición del relé de distancia aumentan con el incremento de la potencia de cortocircuito de la fuente del otro extremo de la línea.
Estos errores en la medición pueden producir demoras innecesarias en la operación del relé que pueden peligrosas para la estabilidad del sistema.