1.- Introducción
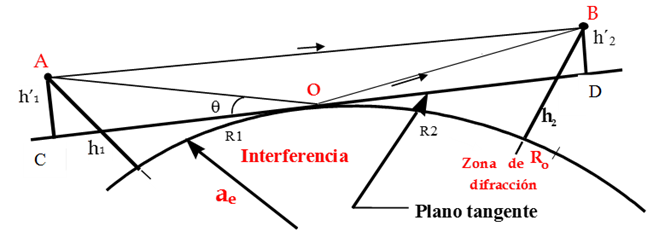
Al pronosticar la cobertura de un emisor de ondas de radio por el nivel de la intensidad del campo eléctrico E en el punto receptor y para el caso de la propagación de las ondas de radio (POR) por el modo de onda terrestre con antenas elevadas, se requiere tener en cuenta la esfericidad de la Tierra debido a su curvatura. Este modo de la POR es predominante en la banda de ondas ultracortas (OUC), a frecuencias por encima de 30 MHz, y se manifiesta como resultado de la interferencia (ver Fig. 1), entre el campo del rayo de la onda directa entre las antenas y el rayo de la onda reflejada, en su forma más simple, sobre una superficie lisa del terreno [1-5]. Por otro lado, es conocido que en la zona lejana de las antenas, a medida que el punto receptor se aleja del emisor, el campo E disminuye debido al efecto de la dispersión por la expansión de los frentes de ondas, así como debido a otros factores como son: la atenuación de la atmósfera por los gases que la componen y los hidrometeoros, las irregularidades de la superficie del terreno, etc., o en el caso del mar, su estado, el que depende de la alturas de las olas. El efecto de las heterogeneidades del terreno ha dado lugar a que el simple modelo de dos rayos que se interfieren sea complementado en modelos híbridos o compuestos, los que posibilitan una mayor exactitud en la determinación del campo [6, 7]. No obstante, se comprende que estos efectos no pueden constituir objeto de este artículo por su complejidad.
En las condiciones ideales de tierra lisa, el campo de interferencia (CI) es calculado, al considerar la esfericidad terrestre, utilizando las alturas reducidas (AR):
Las expresiones que se presentan en la literatura -como resultado de la solución de una ecuación cúbica-, permiten la determinación de las AR, después de hallar las distancias R1 o R2 que se miden hasta el punto de tangencia O (Fig. 1), las que no son conocidas previamente. La dificultad de no conocer de inicio R1 o R2 es solventada en gran medida, para el caso de cortas distancias, conocido como de tierra plana (TP) [1-5, 13], con expresiones específicas válidas solo hasta una distancia Rp (límite de TP) a determinar. La mayor dificultad se presenta para mayores distancias que Rp por que las alturas son afectadas por la esfericidad de la tierra -caso de tierra esférica (TE)-. En ese caso hay que hallar primero R1 o R2, lo que dificulta el análisis de la variación de las AR con la distancia R, o con las alturas de las antenas.
En los párrafos siguientes se expone, de inicio, el algoritmo matemático determinístico presentado en la literatura tradicional, basado en los métodos del trazado de rayos y de la Óptica Geométrica [3-5, 13-15]. En la actualidad los métodos determinísticos [6, 7, 16-23], se mantienen como una alternativa para el cálculo del campo E con resultados satisfactorios similares a los obtenidos con métodos numéricos, y son de aplicabilidad práctica a diferentes entornos [3, 6, 7, 10, 11]: urbanos; rurales con presencia de múltiples obstáculos; sobre el mar, etc. Entre los métodos numéricos se consideran a la vez variantes de solución, por ejemplo: los que emplean la ecuación parabólica (PE), en trayectos simples sobre terrenos irregulares de una vía [24-29], o de doble vía sobre el mar, útil en radar [29]; la Teoría Uniforme de la Difracción -UTD- [30], o las soluciones de ecuaciones integrales de Kirchoff-Fresnel [31-33]. Sin embargo, los métodos numéricos, en general, requieren más tiempo de cómputo [18] y pueden estar comprometidos por los medios computacionales disponibles.
Con lo expresado se quiere significar la robustez con que se mantiene en la actualidad la aplicación de los métodos determinísticos, en forma simple o combinados como métodos híbridos, en diferentes alternativas, y la conveniencia de fortalecer los algoritmos empleados en los mismos. En el trabajo se expone, a continuación de la síntesis del algoritmo tradicional, la secuencia de cómo se han obtenido las expresiones derivadas de las tradicionales propuestas, las que se considera constituyen una alternativa para el cálculo de las AR y, sobre todo, para facilitar el análisis de la dependencia de estas alturas de la distancia R o de las alturas reales.
La contribución principal del presente trabajo es una propuesta de expresiones, novedosas a juicio del autor, y no conocidas en la literatura, para el cálculo de las AR, de las que se derivan curvas de su dependencia de la distancia R normalizada respecto a la DMVD (Ro) -la cual se define en el próximo párrafo- y de las alturas normalizadas de las antenas. Estas expresiones son válidas para todo el rango de distancias hasta Ro. El objetivo principal del artículo es exponer el fundamento científico matemático de esta proposición y significar su novedad.
En un contexto práctico, al determinar coberturas de estaciones de radio, al calcular líneas de radioenlace, o definir el alcance de un radar, en los cuales se requiera un cálculo secuencial de las AR con R, es conveniente contar con expresiones que de forma directa permitan, además, el análisis de su variación con la distancia y la relación de alturas. Mayor importancia adquieren esas expresiones al desarrollar programas secuenciales con ayuda de MCD (computadores digitales). Precisamente estas expresiones fueron utilizadas en los cálculos de las coberturas para sistemas de comunicaciones móviles y de TV descritos en las referencias [9, 10].
2.- Expresiones tradicionales de cálculo de las ar
En esta sección se hace un breve recuento de las expresiones que se emplean tradicionalmente para calcular las AR y se dan a conocer, además, otras expresiones aproximadas que han sido propuestas y que merecen una valoración. El punto de partida son los datos que se relacionan con la Fig. 1. Las AR, sobre una TE, lisa y con atmósfera refractiva, son calculadas usualmente a partir de las relaciones [1-5]:
donde:
donde: R1, R2 - son las distancias entre el transmisor (receptor) y el punto O de reflexión de la onda en el terreno; a = 6370 km, es el radio medio de la Tierra y R ( R1+ R2. Se observa que en estas expresiones se consideran los efectos de la refracción de las ondas en la atmósfera a través del factor de radio ficticio k, pues, en condiciones refractivas, es necesario emplear, en vez de a, el radio ficticio de la Tierra: ae = ka, en la región de estudio. En condiciones no refractivas, k=1.
Cuando el trayecto de propagación tiene una longitud R muy inferior a la distancia máxima de visibilidad directa (DMVD) hasta el horizonte Ro (expresión 8), o sea en una condición próxima a la de una TP, es válido escribir al considerar que los triángulos son semejantes en la Fig. 1, que [1-4]:
y
Al sustituir las expresiones (4)y (5) en (1) y (2), se obtienen las conocidas expresiones de las AR para el caso de TP:
en las que R, a y h, deben tomarse en metros.
Más allá del límite del horizonte Ro, en ausencia de visibilidad directa, el CI debe ser nulo, por lo que predomina el campo de difracción [1,2,3,4,5]. Lo expresado se confirma en la fórmula cuadrática de Vvedenski [1-6], según la cual, en las condiciones de TE, el CI es proporcional al producto de las alturas reducidas: h1( y h2(, y no de las reales. Entonces, es necesario que en Ro, al menos una de esas alturas sea nula. No obstante, al sustituir R en (6) y (7) por su valor extremo Ro, siendo:
no se logra anular el valor de las AR. Para ello, es necesario modificar las expresiones (6) y (7), lo cual requiere que las alturas de las antenas:
En la referencia [1]se considera la coordenada relativa k1 para R1, y se definen los parámetros auxiliares Ao y Bo, o sea:
expresiones estas en las que se han incluido las condiciones de una atmósfera refractiva.
Con estas relaciones, las fórmulas (1) y (3) para una TE, se transforman en:
y
Aquí, R2 = R - R1 = R(1- k1). Compárese las expresiones (12) y (13) con las expresiones (6) y (7).
Es de notar que al considerar (4), k1 toma el valor:
característico del caso de TP. Sin embargo, si (R( Ro), k1 debe tomar el valor:
Esto muestra la variabilidad de k1 al variar R y su dependencia de las alturas. Cuando h1 = h2, k1 = 0.5 en ambos casos.
De la geometría de la Fig. 1, como (R >> h1,2) el ángulo de incidencia sobre el plano tangente es igual al ángulo de reflexión y se obtiene que los triángulos AOC y BOD son semejantes, por lo que:
Al considerar en (16) las expresiones (12-13), se obtiene [1,2]:
y al despejar se logra una ecuación de tercer grado de la variable k1, o sea:
aquí: Co = 1- (Ao + Bo). La dificultad de la solución de (18) es que sus parámetros no son constantes, pues dependen de R.
De las tres raíces de la ecuación cúbica se identifica una sola solución válida, lo que se deduce de las gráficas de cada solución respecto a k1, lo cual está en correspondencia con el proceso físico presente. Otra variante de solución del problema propuesto es aquella en que en vez de k1, se halla R1[4-5, 14-15]. La solución trigonométrica en ese caso se expresa por:
donde p y ( vienen dados por [4, 15, 34, 35]:
Se ha supuesto hasta ahora que: h2 ( h1. Si h1 ( h2, entonces, en (21) se pone (h1 - h2) y en la expresión (19) se obtiene R2[5]. Al contar con R1 (o R2), se hallan las alturas sobre el plano tangente al punto de reflexión O mediante las expresiones (6) y (7). Como se ve en estos casos, la solución no es directa, requiere hallar primero R1 o R2; en la literatura se señala [3,4] que la solución requiere cálculos secuenciales voluminosos y ha sido obtenida durante mucho tiempo por medios gráficos [3]. Por ese motivo, y para facilitar los cálculos, en las referencias [1,2] se han propuesto soluciones más sencillas y válidas para todo R al tomar:
Es evidente que con esta proposición, cuando R( Ro, los valores de
En determinadas aplicaciones radiotécnicas, por ejemplo, al realizar cálculos de coberturas de los emisores de OUC (antenas elevadas), sobre determinadas áreas del terreno, o sobre trayectos (carreteras, caminos, etc.), es necesario predecir la intensidad del campo E en un gran rango de distancias. Los radios de cobertura pueden alcanzar decenas de km y, a veces, acercarse a la DMVD, por tanto, el cálculo de k1 requiere el empleo de expresiones directas fiables y aplicables a todas las distancias.
A continuación, se expone una alternativa de solución analítica al problema, a partir de las relaciones propuestas por Kalinin, planteada en (18), y que son equivalentes al procedimiento de Domb [3-5, 14-15]. Con esta proposición alternativa se obvia la recurrencia analizada en el párrafo anterior.
3.- Propuesta de expresiones alternativas para el cálculo de las AR
Primero, a partir de (17), planteada por Kalinin, se transforma la ecuación cúbica (18) y sus parámetros. La solución, derivada de las expresiones originales, debe facilitar el análisis del comportamiento de las AR al variar R; se considera:
para lo cual se ha tomado: k1 = (y + 0.5), como variable de transformación. Para esta ecuación, con el empleo de las expresiones propuestas en [34], y las relaciones (9-11) se obtiene:
La mayor dificultad para encontrar una solución analítica radica en el discriminante de la ecuación (24) dado por:
en las cuales:
y
En este punto se puede tomar el camino de la determinación de k1 siguiendo (18), o plantear la solución a través de R1, tal como propuso Domb, lo cual ya se ha visto en las expresiones (19-21). Para ambos casos, las relaciones (12) y (13) se pueden escribir de un modo más compacto como:
Se evidencia que las funciones: g((, m) y g(((, m) dependen de los valores relativos de distancia ( y de alturas m. La mayor virtud de la definición de estas funciones consiste en que, para cada juego de valores ((, m), se puede visualizar rápidamente el grado de influencia que la esfericidad de la Tierra tiene en las alturas reducidas de las antenas y su intervención en el CI.
Dentro del rango de distancias hasta Ro, o sea, cuando: 0< (( 1, debe lograrse que las funciones g y g ( cubran el rango: (0 ≤ f((, m) ≤ 1). De las gráficas de de yn (expresión 27), esta condición se obtiene solo para n = 2. De inicio se ha tomado:
Por otro lado, la expresión de Ro, en función de m puede escribirse de dos maneras:
o
y las relaciones (10) y (11), se transforman en:
donde:
Ahora, al seguir el camino propuesto por Domb (expresiones 19-21), y al utilizar estas en la expresiones primarias (1) y (3), las funciones g(R, h1) y g((R, h2) se presentan como:
donde:
y
Con ello, finalmente, las expresiones (36) y (37) se expresan como:
Para el caso particular de una TP, estas expresiones se simplifican y se obtiene:
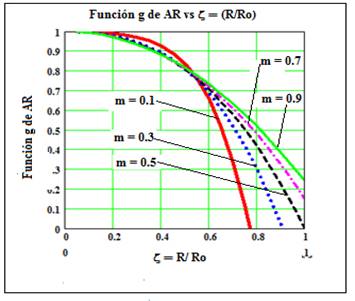
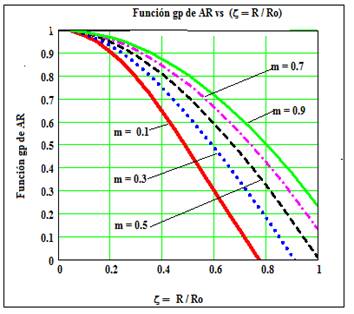
Las gráficas de las funciones:
Es de gran interés conocer previamente hasta que distancia pueden emplearse las expresiones (42) y (43) para TP sin cometer un error apreciable. Para definir la situación se ha graficado el error (o que se comete al comparar los resultados que se logran mediante estas expresiones y los hallados mediante las más completas: (40) y (41). El error relativo (en %) se ha definido a partir de la expresión (44) y se muestra en las Figs. 4 y 5, para dos valores diferentes de m: (m= 0.1 y 0.9), cercanos a los extremos de su rango de variación:
El análisis de ambas figuras evidencia dos cosas:
Primero: (o (ó (op) es pequeño (menor del 3%) si: R < 0.3 Ro, lo cual ocurre en ambos valores de m. Similares resultados pueden mostrarse para otros valores intermedios.
Segundo: El resultado confirma que las expresiones más simples para la condición de TP se pueden considerar “solo para un rango pequeño de distancias” [1-5], el cual se propone definir hasta: RTP ( 0.3 Ro. Con frecuencia, el rango de TP se ha tomado hasta R ( Rp, donde se considera:
La relaciones normalizadas en la expresiones g y g(, generaliza estas funciones de tal modo que con ellas se puede determinar fácilmente el cambio de curvatura con la distancia, o sea se pase de TP a TE y con ello se pueda cambiar las expresiones de pronóstico de la intensidad del CI (región de visibilidad). Estas características facilitan, además, el análisis del comportamiento de las AR en dependencia de los factores (R y h), o en su lugar de los valores normalizados m y (. Nótese que en las expresiones (2) y (3) -o también las (6) y (7)-, las AR dependen recurrentemente de R y h, mientras que en (30) y (31) la AR sólo depende de h. Por ejemplo ¿Cómo hallar la distancia límite Rv donde comienza la dependencia cuadrática del campo respecto a R, si ese valor límite de R depende del producto de las AR y se necesita conocer Rv para hallar esas alturas? [3]. El valor de Rv determina el cambio que debe hacerse de la expresión completa del CI a la expresión cuadrática de Vvedensky [6] dentro de todo el rango de R.
En forma similar pueden valorarse las expresiones (22) y (23), las que pretenden determinar las AR en forma muy simple en todo el rango de distancias (o de (). Se evidencia que estas expresiones no tienen en cuenta las alturas de las antenas, por lo que el error (R1 (definición en la expresión 45) que se comete es significativo, sobre todo para pequeños valores de m (observe la Fig. 5),
En resumen, los resultados muestran que las expresiones alternativas (40) y (41) propuestas son válidas para cualquier distancia R, incluso cerca de Ro, y son aplicables a cualquier relación de alturas m (siempre que m sea menor que 1).
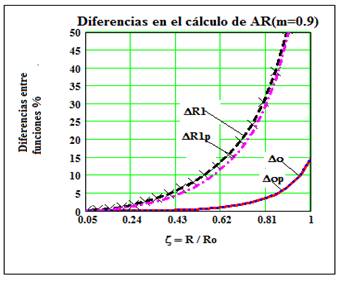
Figura 4 Diferencias de las funciones g o g( en: TP ((o) y respecto a (22) y (23), (R1, al variar ( para m=0.9
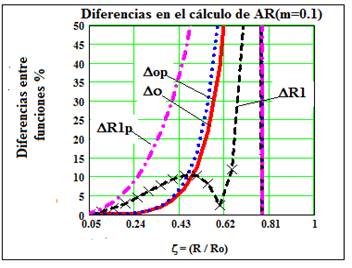
Figura 5 Diferencias de las funciones g o g( en: TP ((o) y respecto a (22) y (23), (R1 al variar ( para m=0.1
Hay que recordar que las gráficas presentadas, y los análisis realizados, han supuesto que h1 < h2. Si h2 < h1, las expresiones (40) y (41) se intercambian, es decir g se emplea en el cálculo de h2( y g( en el de h1( [5,14]. De este modo la aplicación de estas expresiones o sus gráficas al cálculo de las AR sobre TE es universal.
Los experimentos realizados para áreas rurales y urbanas [9-10] y publicados han mostrado una correspondencia aceptable [24] entre los valores calculados y los medidos de la intensidad del CI en trayectos de decenas de kilometros del servicio móvil terrestre (SMT). Como el CI está intrínsicamente ligado a la presencia de las AR en una TE lisa, a lo cual se añaden otros factores, -algunos de ellos mencionados anteriormente-, los resultados de estas mediciones validan el resultado de los algoritmos de los pronósticos del CI que incluyen las AR. Las expresiones propuestas, además, de ser fiables facilitaron el cálculo de esos pronósticos.
4.- Conclusiones
En el artículo se han propuesto expresiones derivadas, alternativas a las tradicionales, empleadas en el cálculo de las AR sobre una TE durante la POR. Las mismas abarcan cualquier relación m entre las alturas reales y de distancias (, o sea de R respecto a Ro. Por lo expresado se puede afirmar que las expresiones derivadas propuestas y sus gráficas, tienen un uso de carácter general. Además, la generalización facilita el trabajo al realizar la evaluación o el análisis de las AR, o del CI, con ayuda de MCD; o de forma directa a través de las gráficas presentadas para análisis previos o en aplicaciones docentes. De este modo las relaciones propuestas amplían las posibilidades, respecto a las tradicionales. Por estas características las expresiones y las gráficas tienen un carácter novedoso.
En el trabajo se ha demostrado que las fórmulas de TP son aplicables sólo hasta la distancia límite RTP, la cual ha quedado definida para su utilización en OUC como: RTP = (0.3-0.4) Ro. Este criterio, en opinión del autor, no estaba puntualizado para la POR de antenas elevadas por lo que alcanza un carácter novedoso. Se ha comprobado que las relaciones (22) y (23), aunque más simples, son de empleo limitado, pues el error que se comete es pequeño solo para valores de m superiores a 0.7 y en un rango de distancias R inferior a 0.3Ro.
De lo expresado se considera que las expresiones propuestas son una alternativa al cálculo de las AR y se cumple con los objetivos planteados en el trabajo. Se evidencia de los párrafos anteriores, el valor práctico de las expresiones y sus gráficas, estas últimas al facilitar el cálculo manual de las AR, o al emplear las expresiones como parte de la determinación del CI con ayuda de MCD, al pronosticar las zonas de cobertura de los emisores de ondas de radio de OUC del SMT, como parte del cálculo de líneas de radioenlace o del alcance de las estaciones de radiolocalización, en especial sobre el mar.