Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Mecánica
versión On-line ISSN 1815-5944
Ingeniería Mecánica vol.15 no.3 La Habana sep.-dic. 2012
ARTICULO ORIGINAL
Simulación numérica del coeficiente de concentración de tensiones en grietas de uniones soldadas a tope
Numerical simulation of the stresses concentration coefficient in cracks butt welded joints
Pavel Almaguer Zaldivar
Universidad de Holguín. Facultad de Ingeniería. Holguín. Cuba
RESUMEN
La fatiga es uno de los más complejos fenómenos en el estudio de falla en piezas sometidas a la acción de cargas dinámicas. El objetivo de este trabajo es exponer una metodología basada en el método de los elementos finitos para la evaluación del coeficiente de concentración de tensiones en grietas longitudinales y transversales de uniones soldadas a tope. El material utilizado es el acero AISI 1015 y el electrodo E6013 de fabricación cubana. Se caracterizan los defectos mencionados y posteriormente se varían sus dimensiones para obtener relaciones entre ellas y el coeficiente de concentración de tensiones. Las simulaciones se realizaron con el software CosmosWork 2008. Con esta metodología se obtuvieron nomogramas y ecuaciones que describen el comportamiento del coeficiente de concentración de tensiones en diferentes nodos de la grieta. Los valores del coeficiente de concentración de tensiones obtenidos muestran una correspondencia con la variación de la severidad del defecto.
Palabras claves: coeficiente de concentración de tensiones, simulación, uniones soldadas a tope, grietas, fatiga.
ABSTRACT
Fatigue is one of the more complex phenomenons in the failure of parts under dynamic loads. In this work is pursued as main objective to expose a methodology based on the finite elements method for the evaluation of the stress concentration coefficient in longitudinal and traverse cracks of butt welded joints. The material bases selected to carry out the study it is the steel AISI 1015 and the electrode E6013 Cuban manufacturing. It is carried out a characterization of the mentioned defects and later the dimensions of each defect are varied to obtain relationships between them and the stress concentration coefficient. The simulations were carried out with the software CosmosWork 2008. With the proposed methodology were obtained graphs and equations that describe the behavior of the stress concentration coefficient in different nodes of the crack. The stress concentration coefficient value it is in correspondence with the defects sizes.
Key words: stress concentration coefficient, simulation, butt welded joints, cracks, fatigue.
INTRODUCCIÓN
El mecanismo de fatiga es uno de los más complejos fenómenos en el estudio de falla en piezas sometidas a la acción de cargas dinámicas, se produce por lo general en zonas donde el material es más propenso a sufrir deformaciones plásticas, esto se debe a la presencia de defectos como las inclusiones, porosidades o concentraciones de esfuerzos, los cuales aumentan las probabilidades de formación de grietas o microgrietas por el efecto cíclico de cargas.
La naturaleza esencialmente multiparamétrica del fenómeno de fatiga, en el que la influencia de los distintos parámetros no puede en general considerarse de manera aislada, constituye la razón de la gran dispersión que generalmente acompaña a los resultados experimentales relacionados con este fenómeno. [1]
Resulta excepcional encontrar una rama de la ingeniería mecánica ajena a procesos de soldadura, y dentro de sus aplicaciones casos donde se presenten cargas exclusivamente estáticas; normalmente se presentan cargas variables que generan una falla súbita de la unión soldada bajo esfuerzos menores que los límites de rotura reportados por el fabricante, tanto del material base como del de aporte.
Para el diseño de uniones soldadas sometidas a cargas variables es posible considerar que los puntos críticos a partir de los cuales las grietas de fatiga comienzan a crecer se ubican con frecuencia en el pie de la soldadura o en la raíz, razón por la cual estos puntos se conocen como "puntos calientes" ("hot spots"). Así surge también el denominado "enfoque local", que se basa en el concepto de que la resistencia a la fatiga de la unión está esencialmente determinada por las tensiones y deformaciones actuantes localmente en el "punto caliente", es decir en la discontinuidad geométrica que constituye el concentrador de tensiones más eficaz que contenga la unión. [1]
Según expresa Reina [2] la Zona Afectada Térmicamente (ZAT) de la unión soldada constituye una entalla metalúrgica atendiendo a la reducción de las propiedades mecánicas que tienen lugar en esta zona, de aquí que la evaluación de los diferentes factores que influyen en la respuesta a fatiga de la unión en esta zona sea un aspecto importante a tener siempre en cuenta en las investigaciones. Es conocido que uno de los factores que tiene gran importancia en el comportamiento a fatiga lo es la concentración de tensiones que se produce en los cambios de sección que tienen lugar en las discontinuidades geométricas. Las grietas que pueden producirse en la ZAT por problemas del proceso de soldadura pueden ser iniciadoras de grietas de fatiga. Si a esto se suma la disminución de la tenacidad en esta zona [3] es de esperarse que el fallo por fatiga de la unión se produzca en ella. En la literatura [4] se plantea también la sensibilidad de la raíz de la soldadura y de la ZAT de las uniones soldadas al crecimiento de grietas de fatiga. Las tensiones que aparecen producto al propio proceso de soldadura son la causa de efectos indeseables en la unión al tener una influencia significativa en la vida a fatiga de los elementos ingenieriles [5, 6] . Las tensiones positivas aumentan la relación efectiva de tensiones, por lo que promueven el crecimiento de grietas de fatiga [7] y fractura y si son de compresión favorecen distorsiones y pandeos indeseables que igualmente perjudican el desempeño de la unión [8] . Según [9] las tensiones residuales se relajan alrededor de un 46 % después de ser aplicados 10000 ciclos de carga variable.
Las teorías clásicas para el tratamiento de la fatiga se aplican directamente a materiales sanos, en el caso de la soldadura se habla de uniones soldadas sanas, esto es, sin defectos o con indicaciones dentro de norma. En caso contrario las teorías de diseño clásicas se hacen poco representativas del fenómeno. Cuando se diseñan elementos de máquinas se asumen ciertas hipótesis, tales como la isotropía y la homogeneidad del material en su estructura metalográfica y ausencia de discontinuidades y defectos. Es conocido que en la soldadura nunca es posible afirmar que existan estas características debido principalmente a la existencia de la ZAT [10]. Además Bejerano [11] plantea que las concentraciones de esfuerzos debidas a discontinuidades geométricas son determinantes en el desempeño de la soldadura. Este aspecto también lo trata Ertas [12] quien analiza el comportamiento a fatiga de una soldadura por puntos apreciándose que las dimensiones de los parámetros de la unión influyen en la respuesta a fatiga. Para analizar el comportamiento a la fatiga de uniones soldadas empleando técnicas de mecánica de fractura es necesario calcular el valor del factor de intensidad de esfuerzos de la grieta de fatiga [13] y predecir luego la vida útil de la unión a partir de la Ley de Paris.
El objetivo de este trabajo es proponer una metodología, empleando el método de los elementos finitos, que permita evaluar el coeficiente de concentración de tensiones en grietas longitudinales y transversales de uniones soldadas a tope.
MÉTODOS Y MATERIALES
La concentración de tensiones producto de las discontinuidades geométricas tiene gran importancia en el trabajo de las uniones soldadas. Aún cuando el esfuerzo nominal en la unión sea menor que el límite de fluencia, si en un punto cualquiera de la geometría las tensiones al menos se igualan a dicho límite se puede iniciar una grieta.
Además en la junta aparecen defectos debidos a posibles errores cometidos durante la soldadura y/o la presencia de las tensiones residuales que son los responsables del desarrollo de futuras grietas que provoquen la falla de la estructura. En el texto Practical Fracture Mechanics in Design [14] se presentan 11 posibles defectos que pueden dar inicio a grietas de fatiga, así como los mecanismos que provocan su aparición.
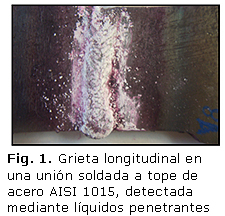
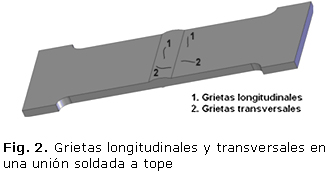
Las grietas son discontinuidades que se presentan como una fractura, tanto en el cordón de soldadura como en el material base. Su existencia tendrá más o menos influencia de acuerdo con el régimen de carga que actúe sobre el conjunto soldado. Su existencia implica una fuerte disminución de la resistencia a la fatiga, porque al actuar las cargas variables el crecimiento y propagación del defecto terminaran en la rotura del conjunto. Las grietas son producidas por problemas de contracción en el enfriamiento o por la velocidad de aplicación. La existencia de grietas puede detectarse mediante el empleo de ensayos no destructivos como el ultrasonido, las partículas magnéticas y los rayos X, incluso mediante una inspección visual es posible ver algunas grietas u otros defectos. Un método de fácil aplicación es el de los líquidos penetrantes, un ejemplo de grieta longitudinal en una unión soldada a tope de acero AISI 1015 determinada mediante el mismo en observaciones efectuadas por el autor se muestra en la figura 1. Por otra parte, Reina [2] clasifica las grietas en longitudinales y transversales de acuerdo a su ubicación respecto al cordón de soldadura (Fig. 2).
Shukla [14] describe los mecanismos de formación de las diferentes grietas, las que una vez formadas se convierten en concentradores de tensiones donde puede comenzar el fallo por fatiga. Normalmente en los cálculos por fatiga la influencia de este factor se considera mediante el coeficiente de concentración de tensiones kσ; este se determina de varias maneras, ya sea por métodos experimentales, por los métodos de la teoría de la elasticidad o mediante los elementos finitos. En este trabajo se expone una metodología para evaluar el comportamiento de este coeficiente mediante la aplicación de los elementos finitos.
Características del material base y del material de aporte
El material base empleado en el estudio es un acero AISI 1015. Este es un acero de construcción, el cual presenta buena soldabilidad metalúrgica, sin tener necesidad de aplicar técnicas auxiliares para garantizar la misma. Este acero pertenece al primer subgrupo de la familia de los aceros de construcción que son los aceros de bajo contenido de carbono [15].
En las tablas 1 y 2 se muestran las propiedades químicas, físicas y mecánicas que posee el acero AISI 1015.

De acuerdo al catálogo UTP 16 y atendiendo a las propiedades mecánicas del material base se escoge el electrodo E6013 que se utiliza para la soldadura de aceros de construcción. En este estudio se emplea un electrodo de fabricación cubana cuyas propiedades mecánicas se muestran en la tabla 3.
Generación del modelo
Las dimensiones del modelo utilizado en el estudio se fijaron basándose en las Normas Cubanas NC 04-72 "Probetas para ensayos de tracción transversal" [17] y NC 08-06:82 "Costura de las uniones soldadas. Tipos y elementos del diseño" [18] obteniéndose un modelo como el que se muestra en la figura 3.
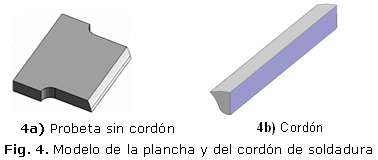
La generación del modelo se realizó con la utilización del software SolidWorks 2008, donde se modelaron primero las dos planchas y luego el cordón de soldadura y por último se ensamblaron las partes para obtener la probeta final. La diferenciación entre las planchas y el cordón de soldadura se efectúa para definir entre las propiedades mecánicas del material base y del material de aporte cuando se asignen los materiales y se ejecuten las modelaciones. En la figura 4 se muestra el modelo por separado de la plancha y del cordón de soldadura.
Las grietas se van a generar en la ZAT de acuerdo a los criterios expuestos antes.
Metodología para la determinación del coeficiente de concentración de tensiones mediante el MEF
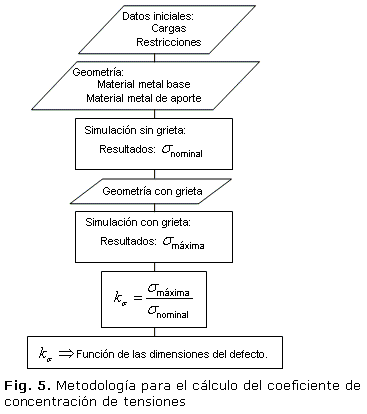
La metodología de cálculo utilizada (Fig. 5) parte de los datos iniciales: las cargas y las restricciones impuestas al modelo.
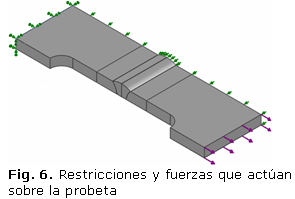
Con el objetivo de que el estudio realizado se semejara lo más posible a los experimentos que se ejecutan en una máquina a tracción se decide que un extremo de la probeta permaneciera inmóvil, por lo que le fueron asignadas restricciones de tipo fijas.
De acuerdo al criterio expuesto en el primer párrafo de esta sección sobre el valor de las tensiones en un punto determinado de la geometría de la junta soldada, se decide aplicar al modelo una carga normal de valor igual a la carga de fluencia. Para determinarla se emplea la fórmula siguiente:
Despejando de la ecuación 1 la carga de fluencia, tomando el área de la sección transversal en la ZAT (definida por el rectángulo de lado 40 mm y altura 4 mm) que es donde se generan las grietas (A =160 mm2) y la tensión de fluencia de la tabla 1, el valor de la carga a aplicar sobre el modelo se obtiene igual a Pf = 50400 N.
Para la realización del estudio mediante el método de elementos finitos se utiliza el paquete profesional COSMOSWorks en su versión del 2008, que es un paquete que trae incorporado el SolidWorks. El estudio realizado se basa en la utilización de un mallado sólido y un análisis estático, se utiliza además un modelo isotrópico elástico lineal, atendiendo a que se considera que en cada parte donde se define un material, este es constante, y que los valores de carga aplicada no superan la carga de fluencia. El tipo de elementos finitos utilizado fue cuadrático de alto orden que producen mejores aproximaciones matemáticas, teniendo 10 nodos por cada elemento, los cuales poseen tres grados de libertad, correspondiéndose cada uno con un desplazamiento en un eje coordenado.
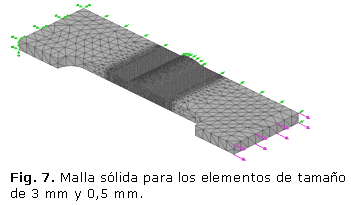
Se realiza un control del mallado con un tamaño del elemento de 0,5 mm en la zona donde se va generar las grietas, que es donde se medirá la tensión nominal y un mallado de 3 mm en la otra parte de la probeta. Esto se aplica con el objetivo de optimizar tiempo a la hora de realizar el mallado y de calcular el valor de las tensiones y para lograrlo se le aplica una línea de partición a la probeta para dividirla en dos partes. También con este mismo propósito de lograr un mejor aprovechamiento del recurso informático y aprovechar la simetría de la probeta, a esta se secciona a la mitad, aplicándole una restricción de simetría en la cara donde se efectúa el corte para realizar el estudio.
La figura 6 muestra la forma en que fueron aplicadas las restricciones y la fuerza a la probeta. Al realizar la división de la probeta y aplicar la simetría solo se aplica la mitad de la carga calculada mediante la ecuación 1.
En la figura 7 se muestra la probeta con el mallado con que se va a realizar el estudio de las tensiones normales en el eje X, dirigido a lo largo de la probeta.
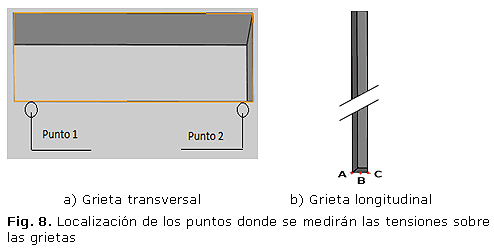
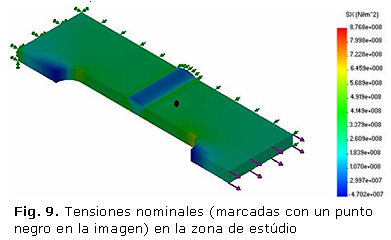
Una vez creada la malla se ejecuta el estudio, se obtienen los valores de las tensiones normales en el eje x y con la herramienta de Identificar valores pueden obtenerse los valores nominales de las tensiones en los puntos donde se va a realizar el estudio. En la figura 8 se muestran los puntos donde se van a medir los valores de tensión en la grieta
Análisis del modelo con grietas
La realización del análisis del modelo con defecto tiene como objetivo el estudio del comportamiento de las tensiones en las grietas transversales y longitudinales de la probeta, para ello se ejecutan varios estudios a la probeta con grietas de diferentes dimensiones y en cada estudio se toman los valores máximos de las tensiones en la grieta, estos puntos donde aparece la máxima tensión en la grieta son los mismos donde deben medirse las tensiones nominales, estos valores serán tabulados (tablas 8 y 9 para las grietas transversales) para las grietas longitudinales y utilizados para determinar el coeficiente de concentración de tensiones.
Para realizar lo expuesto anteriormente se efectuarán un total de 60 estudios para cada uno de los defectos planteados. En las diferentes bibliografías consultadas no se establecen tamaños mínimos ni máximos de grietas, por lo que en esta investigación se decide iniciar los estudios a partir de un tamaño de grieta pequeño y aumentar después las dimensiones hasta que el valor del coeficiente de concentración de tensiones sea elevado.
En el caso de las grietas transversales se toman 6 valores de profundidad, comenzando por 1 mm y aumentando 0,2 mm en cada grieta nueva y para cada valor de profundidad se generan 10 grietas variándole el ancho de la misma desde 0,2 mm hasta 1,1 mm. Valores mayores de las dimensiones de la grieta no son de interés en el estudio debido a la reducción de la resistencia por la disminución del área neta de la sección transversal de la probeta. La longitud de la grieta se mantiene constante con un valor de 5 mm, debido a que este parámetro es paralelo a la acción de la carga de tracción y la variación de su dimensión no influye en el área neta de la sección transversal. La tabla 4 muestra la relación de profundidad y ancho de las grietas.
La misma cantidad de modelaciones se efectúan para el estudio de las grietas longitudinales, manteniéndose constante el ancho de la grieta con un valor de 0,5 mm de acuerdo al criterio de que esta magnitud, al ser paralela a la acción de la carga de tracción su dimensión no influye en el área neta de la sección transversal. Se variarán la longitud de grieta desde 1 hasta 10 mm y la profundidad entre 1 y 2 mm, ver tabla 5. A partir de tamaños valores de las dimensiones de la grieta se produce una reducción importante del área neta de la sección transversal, aumentando el valor de las tensiones normales y por lo tanto, provocando la disminución de la resistencia de la probeta.
Restricciones, fuerzas y mallado en el análisis del modelo con defecto
Por la misma razón expuesta en el epígrafe anterior, de que el estudio se semeje lo más posible a los experimentos que se realicen en una máquina de tracción, las restricciones que se aplicaran a la probeta serán de tipo fijo por un extremo de la probeta y las restricciones de simetría debido al corte aplicado a la probeta con el objetivo de aprovechar el recurso computacional. Al igual que sucede con las restricciones ocurre con las fuerza. Debido a la simetría se aplicará una fuerza normal por el otro extremo de la probeta con el valor de 25,2 kN, que es la mitad del valor calculado antes.
De la misma forma que se genera la malla para el estudio del modelo sin defecto se hizo para los análisis de la probeta con defecto, se realizó un control del mallado en la zona donde se simularon las grietas con un tamaño del elemento de 0,5 mm y en la otra parte de la probeta se le aplicó un mallado de 3 mm.
RESULTADOS
Convergencia del mallado en la muestra de estudio sin defecto
Para comprobar la convergencia en el método de elementos finitos se realizan varios estudios variando el tamaño del elemento y luego se comprueba que los resultados obtenidos no varíen más del 5 % del valor de las tensiones obtenidas con el tamaño del elemento con que se va a realizar el estudio, siempre se medirán el valor de las tensiones en el mismo punto de la probeta. Este análisis de la convergencia del mallado se realiza para los tamaños de los elementos con que fue mallada la probeta. En la tabla 6 se muestran los resultados durante el análisis de la convergencia del modelo sin fisura, para el tamaño del elemento de 3 mm en la zona de la malla gruesa.
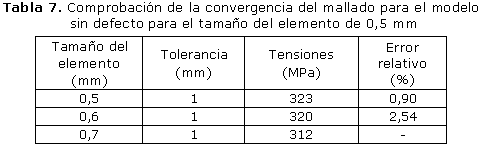
La tabla 7 ilustra los resultados del análisis de convergencia del modelo sin fisura, para el tamaño del elemento de 0,5 mm en la zona donde se quiere determinar las tensiones que se aplicó un control de mallado para refinar la malla y precisar más los valores que se obtengan.
Los resultados de las tensiones nominales fueron de 323 MPa en el punto 1 y 314 en el punto 2 para el caso de las grietas transversales y para las longitudinales se observó que en los tres puntos seleccionados las tensiones eran para el A de 313 MPa; de 314 MPa para el punto B y para el C eran de 314 MPa, valores próximos a la tensión de fluencia reportada en la bibliografía (tabla 1).
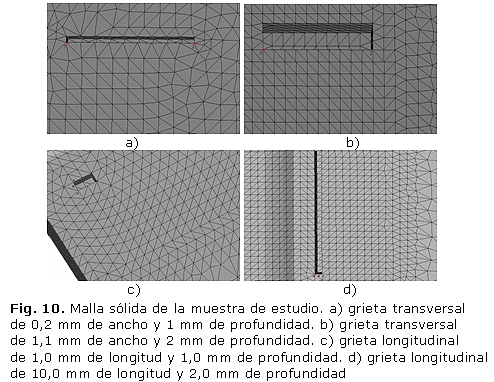
Como muestra de los estudios realizados, para las grietas transversales se presentan los análisis de dos grietas, la primera que tiene como dimensiones 0,2 mm de ancho, 1 mm de profundidad y 5 mm de longitud y la segunda de 1,1 mm de ancho, 2 mm de profundidad y 5 mm de longitud, como se aprecia en la tabla anterior estas dos grietas representan los valores mínimos y máximos de las dimensiones del defecto en el presente estudio. En el caso de las grietas longitudinales se muestran los análisis de las grietas de 1mm de profundidad y 1mm de longitud y de la de 10 mm de longitud y 2 mm de profundidad.
En las figuras 10 a) a la 10 d) se representan el mallado de las grietas que fueron escogidas para presentar su estudio en el presente epígrafe.
Una vez creada la malla se ejecuta el estudio con el objetivo de medir el valor de las tensiones máximas que surgen en la grieta. Para lograr esto se utilizó la opción identificar valores, las figuras 11 a) a la 11 d) muestran los resultados de los estudios desarrollados a los modelos que se mencionaron antes.
DISCUSIÓN
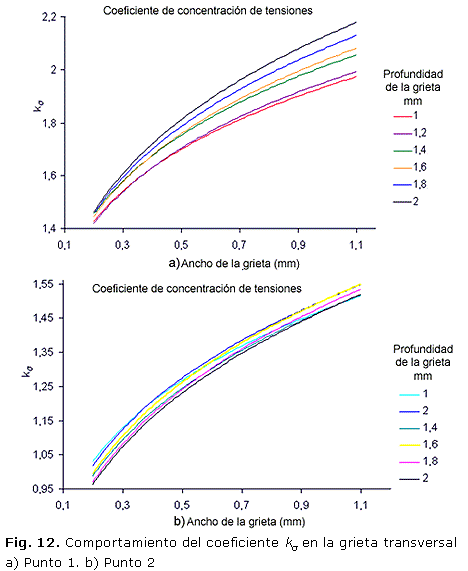
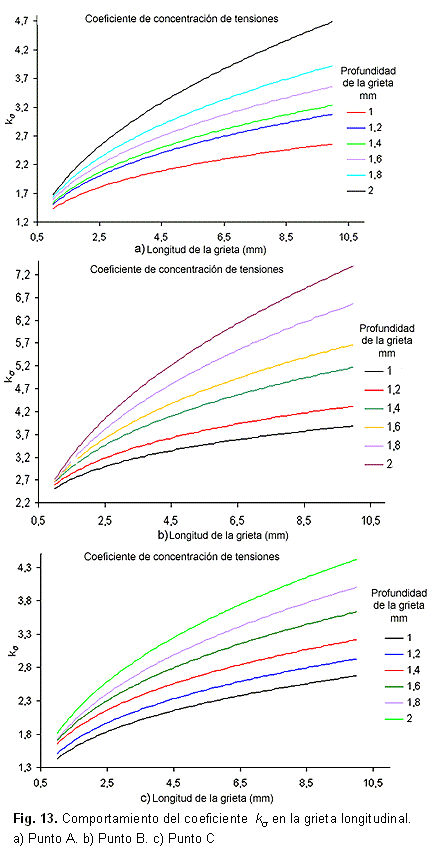
Con la determinación de las tensiones nominales, en el estudio del modelo sin defecto y los valores de las tensiones máximas en cada grieta durante el análisis de las probetas con defecto, se confeccionan nomogramas (Fig. 12 y Fig. 13) que describen el valor de en función de las dimensiones del defecto. También se determina una expresión matemática para cada curva.
Coeficiente de concentración de tensiones en grietas transversales
En las tablas 8 y 9 están los resultados del coeficiente de concentración de tensiones para los puntos 1 y 2 de las grietas transversales.
En la figura 12 se presentan los nomogramas que representan el comportamiento del para los seis valores de profundidad de grietas que fueron estudiadas.
Las fórmulas que permiten calcular el coeficiente para los diferentes valores de las profundidades de grieta se exponen en la tabla 10.
Coeficiente de concentración de tensiones en grietas longitudinales
Las tablas 11, 12 y 13 muestran los valores de tensiones y del coeficiente de concentración de tensiones obtenidos en las grietas longitudinales.
La figura 13 muestra los nomogramas de la variación del coeficiente de concentración de tensiones en las grietas longitudinales en función de la longitud de la misma, mientras que las fórmulas correspondientes se encuentran en la tabla 14.
Los valores del coeficiente de concentración de tensiones obtenidos muestran una correspondencia con la variación de la severidad del defecto. El aumento de las dimensiones de la grietas provoca que el valor de la tensión en el punto analizado sea mayor y por lo tanto se aumenta la probabilidad de fallo. Solo en dos casos (grieta transversal con un ancho de 0,2 mm y una profundidad de 1,8 y 2mm, tabla 9) ocurre que la tensión máxima es menor que la nominal.
De los resultados obtenidos se aprecia que cualquier defecto, por pequeño que sea; es capaz de iniciar una grieta de fatiga. En el caso de las grietas transversales los valores máximos de son menores que los mayores valores para las grietas longitudinales, o sea, los valores máximos de tensión disminuyen en las primeras grietas, por lo que se puede decir que estas van a tener menor incidencia en la respuesta de la unión soldada a cargas variables. Esto se debe a la orientación paralela de las primeras grietas respecto a la carga de tracción. También se destaca el hecho de que en el punto 2 de la grieta transversal, situado más lejos del cordón de soldadura prácticamente coinciden todas las curvas obtenidas, lo que indica poca influencia del ancho de la grieta en el valor de .
CONCLUSIONES
1- Se obtiene una adecuada convergencia (<1,75 %) para el modelo aplicado, tanto para la malla fina (0,5 mm), como para la gruesa (3 mm).
2- La metodología propuesta permite obtener relaciones para el coeficiente de concentración de tensiones de la forma ![]() para las grietas longitudinales y
para las grietas longitudinales y ![]() , para las grietas transversales.
, para las grietas transversales.
3- El coeficiente de concentración de tensiones aumenta junto con las dimensiones del defecto, por lo que de acuerdo con el enfoque local una grieta pequeña donde surjan elevados valores de tensiones ya es suficiente para que ocurra el fallo por fatiga del elemento.
REFERENCIAS
1. Cassanelli Márquez, A., Lombera, A. G. y De Vedia, L. A. "Modelado Numérico del Socavado Lateral en Procesos de Soldadura". Materials Research, 2002. vol. 6. nº. 1. p. 91- 95. ISSN 1516-1439
2. Reina Gómez, M. Soldadura de los aceros. Aplicaciones. 3ra edición. Madrid, España: Gráficas Lormo. 1994. p. 474. ISBN 84-605-14-75-7.
3. Anderson, T. L. Fracture Mechanics. Fundamentals and applications. Third edition. Boca Ratón, Florida. USA: Editorial CRC Press. 2005. ISBN 10:0-8493-1656-1
4. Barsoum, Z., Lundbäck, A. "Simplified FE welding simulation of fillet welds - 3D effects on the formation residual stresses". Engineering Failure Analysis. 2009. vol. 16. nº. 16. p. 2281- 2289. [Consultado el: 11 de julio de 2011], Disponible en: http://www.elsevier.com/locate/engfailanal. ISSN 1350-6307
5. Darcis, P., Katsumoto, H., Payares-Asprino, M. C. et al. "Cruciform fillet welded joint fatigue strength improvements by weld metal phase transformations". Fatigue & Fracture of Engineering Materials & Structures. 2007. vol. 31. p. 125-136. ISSN 1460-2695. DOI 10.1111/j.1460-2695.2007.01205.
6. Liljedahl, C. D. M., Zanellato, O., Fitzpatrick, M. E. et al. "The effect of weld residual stresses and their re-distribution with crack growth during fatigue under constant amplitude loading". International Journal of Fatigue. 2010. vol. 32. p. 735-743. [Consultado el: 11 de julio de 2011], Disponible en: http://www.elsevier.com/locate/ijfatigue . ISSN 0142-1123, DOI 10.1016/j.ijfatigue.2009.10.012
7. Milán, M. T., Bosefilho, W. W., Ruckert, C.O. et al. "Fatigue behaviour of friction stir welded AA2024-T3 alloy: longitudinal and transverse crack growth". Fatigue & Fracture of Engineering Materials & Structures. 2008. vol. 31. p. 526-538. ISSN 1460-2695, DOI 10.1111/j.1460-2695.2008.01234.
8. García, Y. et al. "Obtención de Tensiones residuales a lo largo de un cordón de soldadura mediante métodos analíticos y experimentales". Soldagem Insp., 2006. vol. 11, nº. 2, p. 93-101 ISSN 0104-9224
9. Pei-Yuan, C. "Influence of Residual Stress and Heat Affected Zone on Fatigue Failure of Welded Piping Joints". PhD thesis. North Carolina State University, North Carolina. USA: ProQuest, UMI Dissertation Publishing. 2011. ISBN 10: 1243587814.
10. Bullón C. W. "Simulación de un proceso de soldadura mediante un modelo termo-mecánico considerando el efecto de esfuerzos residuales utilizando el método de los elementos finitos". En: Memorias del 8º Congreso Iberoamericano de Ingeniería Mecánica. Cusco. 2007. p. 13.
11. Bejarano U. et al. "Consideraciones de diseño y factores que afectan el desempeño de las uniones soldadas bajo carga cíclica". En: Memorias del 8º Congreso Iberoamericano de Ingeniería Mecánica. Cusco. 2007. p. 9.
12. Ertas, Ahmet H. y Sonmez, Fazil O., "A parametric study on fatigue strength of spot-weld joints." Fatigue & Fracture of Engineering Materials & Structures. 2008. Vol. 31. p. 766-776. ISSN 1460-2695. DOI 10.1111/j.1460-2695.2008.01263.x
13. Puchi-Cabrera, P. S., Saya-Gamboa, R. A., Barbera-Sosa, L., et al. "Vida a la fatiga de juntas soldadas del acero inoxidable AISI 316L obtenidas mediante el proceso GMAW". Revista de Metalurgia. 2007. vol. 43. nº. 3. p. 215-227. [Consultado el: 2 de febrero de 2011], Disponible en: http://revistademetalurgia.revistas.csic.es/index.php/revistademetalurgia/article/view/67/67. ISSN 1988-4222
14. Shukla, Arun. Practical Fracture Mechanics in Design. New York, Estados Unidos: Marcel Dekker. 2004. p. 525. ISBN 978-0-8247-5885-1.
15. Guliáev, A. P. Metalografía. Moscú: Editorial Mir. 1978. p 333.
16. UTP Catálogo de Electrodos. México. D. F.: Ediciones Académicas Clavería S.A de C.V. 2002.
17. Oficina Nacional de Normalización. Cuba. Probeta para ensayos de tracción transversal en uniones soldadas a tope. NC 04-72. La Habana. Cuba: Oficina Nacional de Normalización. 1972.
18. Oficina Nacional de Normalización. Cuba. Costura de las uniones soldadas. Tipos y elementos del diseño. NC 08-06:82. La Habana. Cuba. Oficina Nacional de Normalización. 1982.
Recibido: 21 de noviembre de 2011.
Aceptado: 6 de julio de 2012.
Pavel Almaguer Zaldivar. Universidad de Holguín. Facultad de Ingeniería. Holguín. Cuba
Correo electrónico: pavel@facing.uho.edu.cu