Introducción
La presencia de las grietas de fatiga en los elementos de máquinas o en las estructuras es un fenómeno indeseable. Para los ingenieros e investigadores la predicción de la vida remanente de algún elemento cuando se detecta una grieta es un tema de vital importancia para tomar decisiones sobre continuar la explotación o pasar al mantenimiento o reparación.
Los diferentes modelos de crecimiento de grietas por fatiga se presentaron en [1]. En este trabajo se analizaron y discutieron las ventajas y desventajas de los diferentes modelos, teniendo en cuenta condiciones como la facilidad de aplicación, la disponibilidad de datos y la validez con respecto a los resultados experimentales. Se concluyó que, en las condiciones del estudio, la Ley de Paris era el método matemático a usar en un contexto práctico, aunque sus resultados son aproximados. Otros modelos más refinados pueden usarse en la medida en que se disponga de suficiente información experimental. El método de elementos finitos extendido puede usarse en conjunto con la Ley de Paris u otras leyes más refinadas para modelar geometrías y condiciones complejas de crecimiento de grietas por fatiga.
Se realizó una breve revisión de los métodos existentes para determinar el SIF, Factor de Intensidad de Tensiones (Stress Intensity Factor, SIF) en [2]. Estos se clasificaron en tres grupos: métodos analíticos, de elementos finitos y experimentales, planteando algunas ventajas, desventajas y restricciones de cada uno de ellos. Se puso de manifiesto la importancia de los elementos finitos, debido a su enorme versatilidad.
En [3] se estudió el cálculo del SIF en placas de acero bajo configuración de carga uniforme. Se compararon los resultados obtenidos por diferentes metodologías como la analítica, el método de colocación del contorno implementado en el software libre MAXIMA y el Método de Elementos Finitos (MEF). Los modelos realizados con el programa ANSYS para la simulación por el MEF mostraron a este como un instrumento confiable para modelar problemas de fractura bajo diferentes configuraciones de geometría. Los resultados experimentales de la trayectoria de propagación de fisuras por fatiga en cinco probetas de acero de alta resistencia se presentaron en [4]. Se realizó la simulación numérica con el software ANSYS MECHANICAL APDL implementando tres criterios para determinar la dirección de propagación. Con estos se alcanzaron resultados prácticamente idénticos respecto a los resultados experimentales. De esta manera se demostró una fuerte correspondencia entre los resultados experimentales y numéricos.
Martins. et al [5], evaluaron experimental y numéricamente el crecimiento de fisuras por fatiga para dos tipos de aceros inoxidables austeníticos, el AISI 316L y un acero de alta resistencia al Cr-Mn. Los autores usaron métodos ópticos para determinar el tamaño de grieta y el MEF para calcular el SIF en los modos I y III. En otra investigación [6], se realizó el análisis experimental y numérico del crecimiento de grietas de fatiga en recipientes a presión de paredes gruesas. Se utilizó la ley de Paris en la evaluación del crecimiento de la grieta.
En la búsqueda bibliográfica realizada se observa que la mayor cantidad de estudios para evaluar el SIF se realiza para los modos de falla I [7-11] o II [8,10,11]. En [12], se realizó un estudio experimental y numérico de la influencia del taladro desviador en la propagación de fisuras para modos de carga mixto I+II. Los estudios en el modo III son escasos [5,10-11]. Suresh, et al., [11] plantean que cuando hay combinación de modos de fractura se pueden despreciar los modos II y III. En todas estas investigaciones se ha utilizado el método de los elementos finitos para evaluar el SIF. Sin embargo, numerosos elementos de máquinas y estructuras son solicitados por cargas torsionales. Por esa razón es necesario conocer la relación que existe entre las dimensiones del elemento y de la grieta para evaluar el SIF en elementos torsionados. El objetivo de este trabajo es presentar una ecuación para evaluar la función de forma en probetas de sección transversal cuadrada solicitadas por torsión cíclica simétrica. A las probetas se les maquinó una pre-grieta en una cara de la sección transversal para inducir el fallo de la misma. Mediante la combinación de los resultados experimentales y del análisis mediante el MEF se obtuvo la función de forma buscada.
Métodos y Materiales
Para esta investigación se construyeron probetas de acero AISI 1015 diseñadas a partir de la consulta de diferentes normas. Los ensayos se realizaron usando una máquina diseñada y construída en la Universidad de Holguín [15]. Se realizó el estudio del comportamiento del SIF y la simulación empleando el Método de los Elementos Finitos [MEF) con el complemento Simulation.
Probeta de sección rectangular para realizar los ensayos a torsión cíclica simétrica
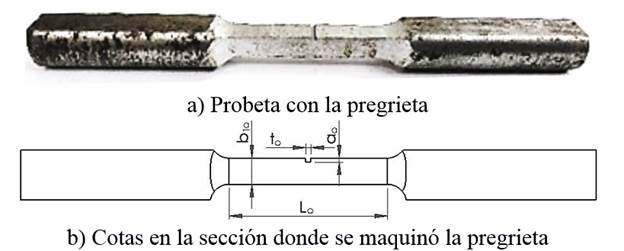
La probeta para realizar los ensayos a torsión cíclica simétrica se muestra en la figura 1a. En el centro de la probeta se observa la pregrieta realizada para inducir el fallo.
En la figura 1b se expone la probeta con las diferentes cotas. Estas son:
L0: Longitud de la probeta en la zona de ensayo.
a0: Longitud inicial de la grieta.
t0: Ancho inicial de la grieta.
b10: Ancho de la cara 1. Se corresponde con la cara en la que se mide el crecimiento de la grieta.
b20: Ancho de la cara 2. Es la cara perpendicular a la que se realiza la medición del crecimiento de la grieta.
Esta no se representa en la figura 1b.
Se consultaron diferentes normas ASTM para proponer la forma y dimensiones de esta probeta: E 2207-02 Standard Practice for Strain-Controlled Axial-Torsional Fatigue Testing with Thin-Walled Tubular Specimens, E 2368-04 Standard Practice for Strain Controlled Thermomechanical Fatigue Testing, E 466-96 Standard Practice for Conducting Force Controlled Constant Amplitude Axial Fatigue Tests of Metallic Materials, E 468-90 Standard Practice for Presentation of Constant Amplitude Fatigue Test Results for Metallic Materials y E 606-92 Standard Practice for Strain-Controlled Fatigue Testing. En todas se presentan probetas de sección transversal circular. Se observó que las probetas tienen la sección central con un menor diámetro lo que garantiza que el fallo ocurra en esa zona. Por esa causa la configuración de la probeta propuesta en esta investigación para realizar los ensayos a torsión cíclica simétrica tiene la sección transversal cuadrada de dimensiones menores que en la zona de agarre con el cabezal. Los extremos de la probeta tienen una cara plana para lograr el agarre en los cabezales de la máquina. Se realizaron cuatro experimentos. Para tomar esta decisión se utilizó la norma ASTM E 8M-04 Standard Test Methods for Tension Testing of Metallic Materials. Esta norma expresa que en los ensayos los estudios de repetitividad y de reproducibilidad son importantes. Para ello se deben realizar dos o tres mediciones de cada experimento como mínimo. Es necesario destacar que la norma ASTM E 8M-04 se aplica a los ensayos a tracción, se utilizó para inferir el número de probetas porque no se cuenta con una norma para realizar los ensayos descritos en este trabajo.
Las probetas se fabricaron de acero AISI 1015. La tabla 1 expone las propiedades del acero utilizado.
Tabla 1 Propiedades mecánicas del acero AISI 1015. (http://www.matweb.com)
| Propiedad | Valor | Unidad |
|---|---|---|
| Límite elástico σy | 315 | MPa |
| Límite de rotura σr | 420 | MPa |
| Módulo de Young |
200 | GPa |
| Módulo de elasticidad de segundo orden |
80 | GPa |
| Coeficiente de Poisson µ | 0,29 |
Máquina de ensayos
Los ensayos se realizaron en la máquina torsional para ensayos a fatiga construida y diseñada en la Universidad de Holguín. Las características de esta máquina se explicaron en [15]. En ese mismo trabajo se definió un procedimiento que permitió obtener una ecuación para la función de forma en probetas de sección transversal circular. Los mismos pasos definidos en esa investigación se siguieron en la presente para evaluar la función de forma en probetas de sección transversal cuadrada con una pre-grieta en una de las caras.
Cálculo del factor de intensidad de tensiones
En las probetas preagrietadas de sección cuadrada se realizó el estudio del comportamiento del SIF. Este es posible calcularlo según la ecuación 1. Esta es una adaptación de [7]. Esos autores determinaron el SIF en el modo I de fallo, donde calcularon los desplazamientos normales a la grieta y utilizaron el módulo de elasticidad de primer orden. La técnica utilizada en esa investigación se denomina Desplazamientos de Apertura de la Punta de la Grieta (Crack Tip Opening Displacement, CTOD). Este modelo es teórico y de fácil aplicación ya que depende de factores geométricos y del tipo de material. Presenta una buena aproximación al modelo de crecimiento de grieta por fatiga [2].
Donde:
G |
- es el Módulo de elasticidad de segundo orden, es igual a 80 GPa. |
L |
- es la longitud de los elementos singulares. |
µ |
- es el coeficiente de Poisson. |
V i |
- son los desplazamientos paralelos a la superficie de la grieta. |
El SIF también se calcula es mediante la ecuación 2:
Donde:
Y |
- es la función de forma y depende de la geometría de la probeta y de la grieta. |
τ |
- Tensión tangencial nominal. Este valor se determina mediante las expresiones analíticas de la teoría de la Resistencia de Materiales, o sea, considerando el cuerpo ideal, sin la presencia del defecto. |
a |
- es el tamaño de grieta. |
Como se aprecia en las ecuaciones 1 y 2, las dificultades para determinar el SIF se presentan en la determinación de los desplazamientos en la punta de la grieta, cualquiera que sea el modo de falla y la función de forma. Una manera de conocer los desplazamientos en la punta de la grieta es el MEF. La función de forma, para geometrías conocidas, es posible encontrarla en los manuales de Mecánica de la Fractura.
Simulación del estado tensional - deformacional en la probeta
En esta investigación se utilizó el MEF para evaluar el estado tensional en las probetas. Para ello se modeló la probeta en el programa SolidWorks 2016. El modelo inicial para cada probeta se obtuvo a partir de las imágenes mostradas en las figuras 1a y 1b y los datos presentados en la tabla 1. Después, durante el ensayo se midieron los diferentes tamaños de grieta y se modeló entonces la probeta con cada uno de esos valores. Para realizar las simulaciones se utilizó el complemento Simulation.
Las propiedades del material se definieron según la tabla 1. El modelo constitutivo del material fue isotrópico elástico lineal. A la probeta se le aplicó un momento torsor en un extremo igual a 214 Nm, que se corresponde con la acción del cabezal móvil. En el otro extremo se aplicaron restricciones fijas, que se corresponden con el cabezal fijo de la máquina.
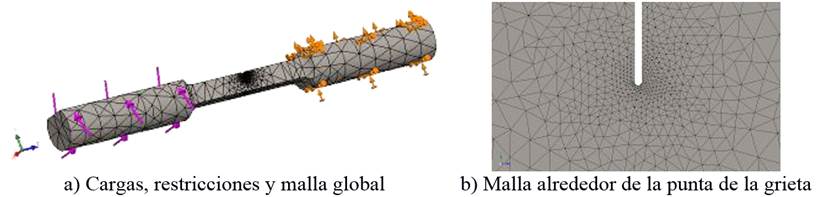
El mallado global se hizo con una malla sólida basada en curvatura. Esta crea más elementos en zonas de mayor curvatura automáticamente. El tipo de elementos es cuadrático de alto orden que representan los contornos curvos con mayor precisión y producen mejores aproximaciones matemáticas. Los dos últimos aspectos permiten mejorar la malla alrededor de la punta de grieta. En esa zona se creó también un control de malla con un tamaño de 0,003 mm y un cociente de crecimiento de 1,5. El tamaño máximo y mínimo de elemento igual a 5,324 mm y 1,065 mm, respectivamente. El número total de elementos es 936 698 y de nodos igual a 1 375 289. En la figura 2a se muestran las cargas y restricciones aplicadas a la probeta, además del mallado global; mientras que en la figura 2b se expone un detalle de la configuración de la malla alrededor de la grieta.
Resultados y Discusión
Aplicación de la carga cíclica sobre las probetas
Siguiendo el procedimiento descrito por [15] se procedió de la siguiente manera:
1. Se montó cada probeta en la máquina de ensayos.
2. Se midieron cada una de las dimensiones de la probeta (b 10 , b 20 , a 0 , t 0 y L 0 ) en la parte donde se indujo el crecimiento de la grieta. Este paso permite conocer todas las dimensiones y evaluar entonces la posible función de forma. Las dimensiones determinadas se expusieron en la tabla 1, en la tabla 2 se resumen las medidas de las cuatro probetas estudiadas.
Tabla 2 Dimensiones de las probetas
| No. | L0 (mm) | a0 (mm) | t0 (mm) | b10 (mm) | b20 (mm) |
|---|---|---|---|---|---|
| 1 | 41,2 | 1,05 | 1,4 | 6,8 | 7,00 |
| 2 | 42,1 | 1,50 | 1,1 | 6,6 | 7,10 |
| 3 | 39,8 | 1,10 | 1,0 | 6,8 | 7,05 |
| 4 | 39,4 | 1,30 | 1,1 | 6,9 | 7,30 |
3. Se aplicó el momento torsor cíclico. El número de ciclos aplicados a la probeta se visualizó en la pizarra del panel de control de la máquina de ensayos. Cada un determinado número de ciclos se pausaba el ensayo para medir el tamaño de la grieta.
En la tabla 3 se muestran los números de ciclos aplicados hasta la rotura a cada una de las probetas ensayadas. Los resultados obtenidos indican que las probetas se comportaron según un régimen de bajo ciclo. El bajo número de ciclos que soportaron las diferentes probetas fue debido a la pregrieta maquinada en ellas.
Tabla 3 Número de ciclos aplicados a las diferentes probetas
| Probeta no. | Cantidad de ciclos N |
|---|---|
| 1 | 503 |
| 2 | 639 |
| 3 | 580 |
| 4 | 661 |
4. Cada un número determinado de ciclos se midió el tamaño de la grieta a n para cada probeta. Este se determinó mediante la inspección por el ensayo no destructivo de los líquidos penetrantes. La figura 3a es la medición en la probeta 4 cuando se le habían aplicado 500 ciclos de carga y la longitud de grieta era igual a 3,01 mm.
La figura 3b muestra la sección transversal de la probeta 4, se puede apreciar que la grieta comenzó a desarrollarse a partir del defecto inicial y creció hasta que se produjo la rotura por la sobrecarga estática. Todas las probetas presentaron la rotura típica por fatiga. Se observó que la grieta creció según círculos concéntricos a la rotura frágil. Hay presencia de bandas de cizallamiento.
Se obtuvo una gráfica, figura 4, que relaciona la longitud de grieta con el número de ciclos aplicados a las probetas. La pendiente de la curva para la probeta 1 tiene un aumento a partir de los 300 ciclos de carga. Las correspondientes a las probetas 2 a la 4, el cambio ocurrió a partir de los 400 ciclos. Esto demuestra que tuvo un crecimiento más inestable de la grieta.
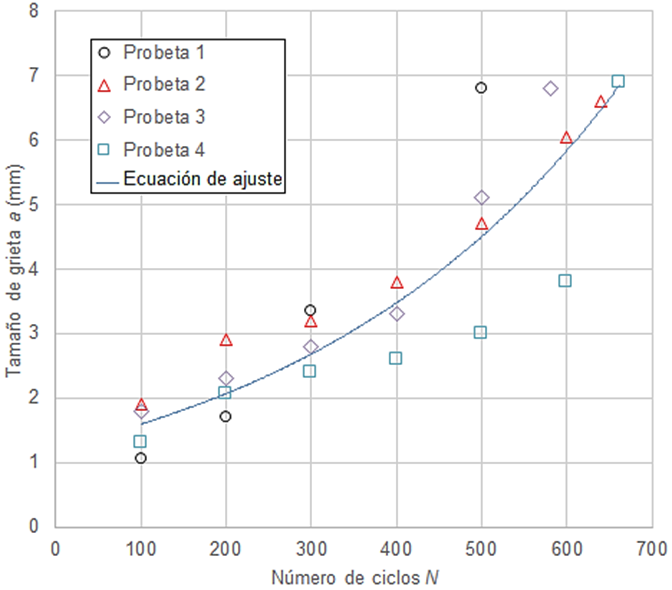
Fig. 4 Relación entre el tamaño de grieta y el número de ciclos de carga en las probetas preagrietadas
Se determinó una ecuación que relaciona el tamaño de la grieta con los ciclos de carga aplicados a la probeta. De esta manera se determinó que existe una relación exponencial dada por la ecuación 3.
El coeficiente R2 es igual a 0,8187. Este valor se considera aceptable.
5. Se modeló la probeta con los diferentes tamaños de grieta medidos en los ensayos realizados. El modelo utilizado se corresponde con la figura 1b. En esa figura se mostró el tamaño inicial de grieta.
6. Se realizaron las simulaciones numéricas. Las cargas, las restricciones y el mallado aplicados a la probeta simulada se mostraron en la figura 2. En la figura 5 están los desplazamientos perpendiculares a la grieta (en la dirección del eje Z, que es perpendicular al plano de la figura) obtenidos en la punta de la misma. La longitud de los elementos singulares se determinó entre los nodos 287 y 204918 o 286 204915 y es igual a 0,001 mm. El SIF calculado según la ecuación 1 para la probeta 4, con un tamaño de grieta de 3,01 mm fue igual a 2 9480,8 MPa·m1/2.

Fig. 5 Cálculo de los desplazamientos perpendiculares a la grieta por el método de los elementos finitos en la probeta 4 con un tamaño de grieta de 3,01 mm
En las evaluaciones de la fractura de los elementos de máquinas, un objetivo es obtener una ecuación que describa la función de forma para la configuración geométrica de la pieza estudiada, las dimensiones de la pieza y de la grieta, la posición de la grieta y el modo de fallo. En este trabajo se propuso una ecuación para la función de forma que relaciona el ancho de la cara sobre la que se mide la longitud de la grieta con el tamaño de grieta. Atendiendo a que los ensayos realizados a las probetas fueron de torsión cíclica, los resultados obtenidos son para el modo III de fallo.
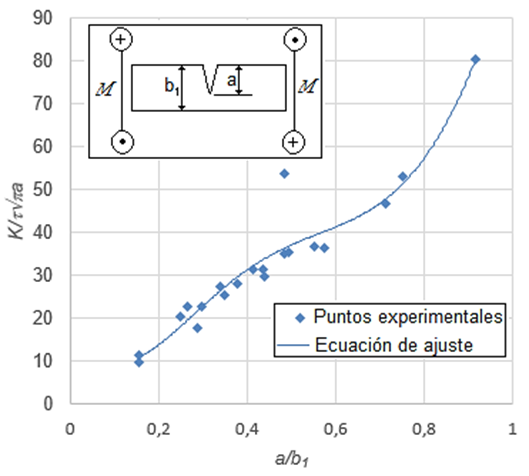
Para ello se igualaron las ecuaciones 1 y 2 y se despejó la función de forma Y. El cociente así obtenido se ubica en el eje de las ordenadas de un gráfico en el que en el eje de las abscisas se corresponde con la relación tamaño de grieta sobre las dimensiones de la cara de la probeta en la que se mide el crecimiento de la grieta (a/b1), figura 6. El ajuste así obtenido, que se corresponde con la función de forma se expone en la ecuación (6):
El coeficiente de ajuste R2 de la ecuación 4 es 0,9225.
La figura 7 expone la relación entre la velocidad de crecimiento de la grieta da/dN y el Factor de Intensidad de Tensiones en el modo de fallo III K III para las probetas torsionadas ensayadas. El aumento del tamaño de la grieta provoca que aumente el Factor de Intensidad de Tensiones. Como se aprecia en la ecuación 2 existe una relación directamente proporcional entre ellos.
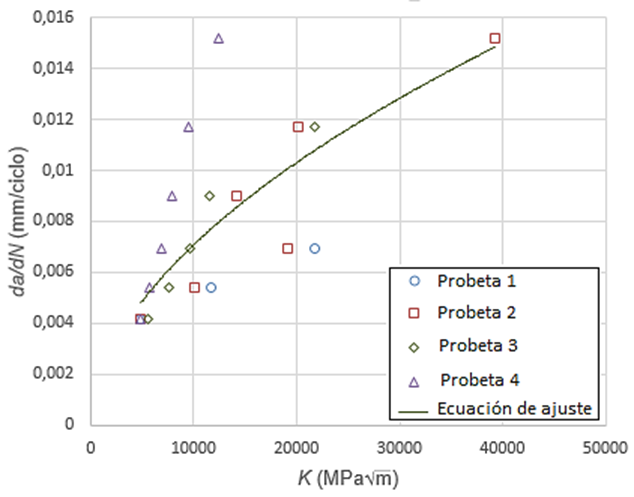
Fig.7 Relación entre la velocidad de crecimiento de la grieta y el Factor de Intensidad de Tensiones
La ecuación de ajuste de los datos mostrados en la figura 7 representa la Ley de Paris, ecuación 5, para las probetas estudiadas. Esta relaciona el SIF con la velocidad de crecimiento de la grieta.
En [16] se evaluó la fractura de planchas soldadas en T. En ese trabajo también se aplicó la CTOD para el cálculo del SIF en los modos I y II, sin embargo no se encuentran referencias al modo III. Igual que en trabajos previos [11], se plantea que el valor del K II es despreciable ante la presencia del modo de fallo I. La ecuación 5 puede ser aplicada para probetas de sección cuadrada solicitadas a cargas cíclicas torsionales (Modo III) con un régimen de fatiga de bajos ciclos. Esto obedece a los resultados de los experimentos con la máquina de ensayos utilizada que aplica estos tipos de carga. La medición del tamaño de la grieta se realizó mediante el método de los líquidos penetrantes. Mejores aproximaciones en la medición del tamaño de grieta son posibles con el empleo de otras técnicas como puede ser una cámara de alta velocidad.
Según [1] el valor del coeficiente m de la Ley de Paris arroja resultados en un rango desde 1,5 hasta 4. En este trabajo se obtuvo igual a 0,5407. La diferencia puede estar dada en el modo de falla estudiado pues como se ha visto el modo III es despreciado en la mayoría de los trabajos consultados.
Conclusiones
Los ensayos realizados a probetas torsionadas preagrietadas permiten evaluar el número de ciclos que resisten las mismas hasta la rotura. La grieta en las probetas comenzó a crecer desde el defecto inicial, desarrollando círculos concéntricos con la zona donde se produjo la fractura final. La combinación de los experimentos con el método de los elementos finitos permitió obtener una función de forma que relaciona el tamaño de la grieta con las dimensiones de la cara de la probeta. A partir de esta ecuación se obtuvo la velocidad de crecimiento de la grieta. La relación entre esta y el Factor de Intensidad de Tensiones en la punta de la grieta, determinado aplicando el método del CTOD permitió proponer una ecuación para la Ley de Paris en probetas de sección transversal en las que se produce el modo de fallo III.