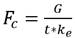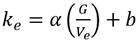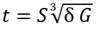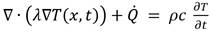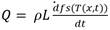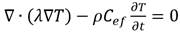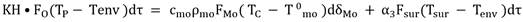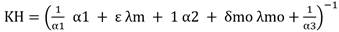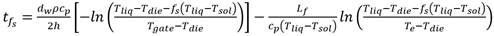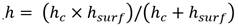Artículo de investigación científica y tecnológica

Diseño de un molde metálico para fundir manillas de freno y embrague de la moto suzuki AX-100

Design of a metal mould for casting brake and clutch levers for a suzuki AX-100 motorbike

0000-0003-4163-2656Victor M. Mir-Labrada^{I  *}  , 0000-0002-0783-5209Tiel García-Hernández^I  , 0000-0002-1211-0333Cristian Luís Pérez-López^I  , 0000-0002-2110-6491Alberto Menéndez-Pérez^II  , 0000-0002-3167-1072Yusleidi Cuesta-Figueroa^III 

^I Universidad Tecnológica de la Habana José Antonio Echeverría, Facultad de Ingeniería Mecánica, Dpto. Ingeniería Mecánica. La Habana, Cuba.

^II Etajoule: Jacksonville, Florida, US.

^III Empresa de Ingeniería del Reciclaje. La Habana. Cuba.

Resumen

El objetivo del trabajo presentado fue el diseño de un molde metálico de fundición por gravedad, para obtener manillas de freno y embrague, de aleaciones de aluminio, para la moto Suzuki AX-100. Se determinaron los esfuerzos máximos a los que se somete la pieza, además, evaluado por el método de elementos finitos, teniendo en cuenta la composición de las materias primas existentes en una empresa, destacando que la pieza obtenida cumple con los requisitos de resistencia. Los resultados de las simulaciones arrojaron que la resistencia era suficiente, por lo que se pasó al diseño del molde metálico. Para su diseño se empleó una metodología establecida, con los modelos de Fourier-Kirchhoff para el régimen térmico, resultando en las dimensiones de este. A su vez se simuló por medio de software de fundición tanto el llenado como la solidificación, pronosticando los comportamientos termodinámicos y los fenómenos transitorios del fluido durante el proceso de vertido. Se obtuvieron valores positivos para la microporosidad, criterio de Niyama, velocidad del flujo y, evolución del sólido. Los resultados permiten asegurar que tanto el diseño como el funcionamiento del molde garantizan la obtención de manillas de forma productiva y libres de defectos.

Palabras-clave: simulación de fundición; fundición en molde metálico; análisis por Elementos Finitos

Abstract

The aim of the work presented was the design of a metal mould for gravity die casting to obtain brake and clutch handles of aluminium alloys for Suzuki AX-100 motorbike. The maximum stresses to which the part is subjected were determined and evaluated by the finite element method, considering the composition of the existing raw materials, highlighting that the part obtained meets the strength requirements. The results of the simulations showed that the strength was sufficient, and so the design of the metal mould was started. For its design, an established methodology was used, with the Fourier-Kirchhoff models for the thermal regime, resulting in its dimensions. In turn, both filling and solidification were simulated by means of casting software, predicting the thermodynamic behavior and the transient phenomena of the fluid during the pouring process. Positive values were obtained for microporosity, Niyama criterion, flow velocity and solid evolution. The results allowed us to ensure that both the design and the operation of the mould guarantee the production of productive and defect-free handles.

Key words: casting simulation; gravity die casting; Finite Element Analysis

Introducción

La fundición por gravedad es un método ancestro que aún en la actualidad se sigue explotando mucho, pero extremadamente complejo en tecnología; la calidad de salida es el resultado de la interacción de muchos factores mecánicos, físicos y químicos.

Un ingeniero diseñador debe concebir el molde metálico como una máquina térmica. La forma de la pieza determina la disposición y distribución, mientras que el tamaño de termina la magnitud de la expansión térmica del molde, de la contracción de solidificación de la aleación y de la insignificante variación de los núcleos o machos.

En las últimas décadas, el desarrollo de herramientas eficientes de Diseño Asistido por computadora (CAD) y de Ingeniería Asistida por computadora (CAE) ha permitido importantes cambios en el mundo de la ingeniería. En la actualidad, el CAD se utiliza ampliamente en industrias, academias y diseñadores autónomos para desarrollar nuevos productos, diseños o procesos. La representación totalmente paramétrica de los objetos permite refinar las ideas antes de implementar un proceso de fabricación, limitando la fuente de errores, así como los gastos. Paralelamente, las tecnologías CAE se explotan para modelar con precisión el comportamiento y apoyar a los ingenieros durante todo el proceso de diseño. Las simulaciones CAE son útiles, por ejemplo, para analizar el movimiento de componentes y ensamblajes, es decir, Análisis Multicuerpo, MBD (Multibody Dynamic) para comprobar deformaciones y tensiones, Análisis de Elementos Finitos (AEF), para simular el sistema de actuación o para realizar estudios de optimización.

En comparación con las pruebas físicas, los modelos virtuales presentan ventajas evidentes en términos de ahorro de costes y capacidad para probar el rendimiento de varias variantes de diseño en un tiempo limitado; gozando de gran popularidad el Método de los Elementos Finitos (MEF), porque resuelve los problemas de valores límite de forma sencilla y sistemática, incluso en casos de geometrías complejas ^[1, ^2]. Este método es capaz de tratar las condiciones de contorno complicadas y su precisión es buena. Algunos de los programas usados para el análisis de piezas obtenidas por fundición que emplean este método son el ProCAST, CAPCAST y Altair Inspire Cast ^[3].

Otro de los métodos de simulación empleado es el método de diferencias finitas FDM (Finite Difference Method), éste se utiliza habitualmente para predecir el flujo de llenado metálico, la transferencia térmica y la solidificación, en muchas suites de simulación de fundición, por ejemplo, MAGMAsoft, NovaCast, Flow-3D, PAM-CAST y AnyCasting. Este método puede obtener muchos datos valiosos en menor tiempo de cálculo que el MEF, y se adapta para modelar las piezas fundidas con una geometría regular ^[3].

Aravind, Ragupathi y Vignesh ^[4] realizaron una simulación por MEF con el software MAGMAsoft, del cuerpo de una bomba de aleación de aluminio obtenida por fundición por gravedad en molde metálico, para encontrar la razón de los defectos, resolver los problemas de transferencia de masa y optimizar el diseño de la mazarota y el alimentador. Eliminando los defectos reales obtenidos, con solo cambiar el espesor del nervio central de 7 a 20 mm y la ubicación de los machos en la parte superior del molde para permitir el escape de los gases.

Pinto et al ^[5] emplearon el software ProCAST para simular la fundición de terminales eléctricos de aleación Zamak, en molde metálico de acero, enfocándose en analizar la fracción volumétrica del aire atrapado, la turbulencia y velocidad de entrada del metal líquido para predecir la aparición de defectos y evitar que los mismos aparezcan. Como resultado, aumentaron la sección del tragadero y de los canales de ventilación, logrando la disminución casi total de los poros finales comprobados experimentalmente.

Patnaik L et al ^[6] realizaron un estudio detallado de los parámetros de diseño del molde metálico para fundición a presión, para obtener la carcasa de un motor de moto, empleando el software MAGMAsoft. Centraron el análisis en la temperatura y tiempo de llenado, aire atrapado, temperatura de solidificación y enfriamiento. Como resultado, modificaron el molde aumentando los vientos y ubicando uno central, comprobando experimentalmente que los resultados son satisfactorios.

Por su parte, Zarbini Seydani et al ^[7], realizaron un estudio empleando el software ProCAST, para simular la fundición por gravedad en un molde de arena con resina. Se enfocaron en validar y confirmar los resultados de la simulación, empleando un molde con cristal transparente, apreciando la precisión de la réplica del proceso de llenado y solidificación, comparado con el resultado del software; obteniendo valores estadísticos de discrepancias del 15,38 % para el tiempo de llenado y del 9,13 % para el tiempo de solidificación.

Vergano et al ^[8] centraron su estudio en la simulación, con el software MAGMAsoft, de la fundición por gravedad de la tapa de un motor de combustión de cuatro cilindros de aleación de aluminio, obtenida en un molde metálico de acero. Realizaron ocho simulaciones, colocando 5 puntos de control térmico en el molde y fijaron la temperatura de vertido en aproximadamente 120 oC por encima de la temperatura del líquido. Llegaron a la conclusión de que la simulación del sistema de alimentación y del vertido es crítico para determinar los defectos en el proceso de fundición por gravedad.

Taniguchi y Maeda ^[9] en su trabajo realizaron una comparación de los resultados de la simulación con el software TopCAST con los resultados filmados con cámara de video, de un molde de arena preparado con un cristal termorresistente transparente para analizar, en fundición por gravedad de una aleación de aluminio, la influencia de seis formas diferentes de alimentador y dos variaciones de formas del vertido. Llegaron a la conclusión de que la velocidad de entrada y el tiempo de llenado se comportaron muy similar tanto en la simulación como experimentalmente.

Por otra parte, Dučić N, Jovičić A et al ^[10], realizaron la simulación empleando el software MAGMASoft y la comprobación experimental, de la fundición por gravedad de un hierro fundido en molde metálico permanente de igual material. Hicieron énfasis en el diseño del molde, el sistema de alimentación y evaluaron la solidificación y el nivel de porosidad. Los resultados de la simulación estuvieron acordes con los resultados experimentales.

En la mayoría de los casos anteriores se establece una comparación de los resultados obtenidos con las simulaciones y con los obtenidos en los experimentos reales. En casi todas se emplearon aleaciones de aluminio vertidas por gravedad y en varios casos moldes metálicos permanentes; en la mayoría se destaca la alta exactitud de los resultados de las simulaciones. Los análisis empleados en estos artículos se tomaron como referencia de criterios para realizar nuestro análisis y simulación posterior.

Para la optimización de la tipología y la reducción de peso de una manilla de embrague de motocicleta los autores Sakti Nur Achmad K A et al. ^[11] utilizaron ANSIS como software para la simulación de las cargas, para una reducción de la masa de un 62,12 % y un coeficiente de seguridad de 1,97 con resultados de deformación menores que el límite elástico de la aleación de aluminio empleada.

De igual modo, Prasetyono, Yudianto, y Adiyasa ^[12], utilizaron el MEF para optimizar una palanca de freno; logrando reducir la masa de la misma un 50,9 % empleando tres tipos de materiales, concluyendo que una aleación de Al como material, contribuye a una masa más ligera en comparación con los otros diseños y materiales evaluados.

El objetivo del trabajo presentado es el diseño de un molde metálico de fundición por gravedad, para obtener manillas de freno y embrague, de aleaciones de aluminio, para la moto Suzuki AX-100. Para lo cual se valorará el esfuerzo máximo real al que se pueden someter las manillas durante su funcionamiento, y determinar si con las composiciones de las materias primas disponibles se logrará satisfacer el valor de resistencia mecánica necesario.

Métodos y Materiales

La construcción de las manillas debe permitir la aplicación de los métodos modernos de elaboración mecánica con los gastos mínimos de trabajo, materiales y tiempo, a fin de facilitar la elaboración del molde en las condiciones y equipamientos disponibles en el taller donde se confeccionará.

Debido a que la demanda de manillas es algo superior a las veinticinco mil unidades, se decidió realizar el diseño de un molde permanente metálico para vertido por gravedad (coquilla), que permite reducir el tiempo de producción, el espacio en el taller de fundición y a su vez elimina los errores humanos del moldeo manual, disminuyendo el rechazo.

Conociendo la composición química, tabla 1 y las propiedades físicas y mecánicas, tabla 2, de las materias primas disponibles en el taller de fundición donde se elaborarán las manillas, se requirió evaluar si estas aleaciones podían satisfacer el valor de resistencia requerido por la pieza durante su funcionamiento real.

Tabla 1 Composición química de las materias primas disponibles, donde el Aluminio es el resto. Fuente ^[13]  

Aleación ASM	Norma DIN 1725	Cu	Zn (máximo)	Si	Fe (máximo)	Ti (máximo)	Ni (máximo)	Mn	Mg	Sn (máximo)	Otros (máximo)
A360	GD-AlSi9Cu3	0,6	0,5	9,0-10,0	1,3	-	0,5	0,35	0,4-0,6	0,15	0,25
A384.0	GD-AlSi12(Cu)	3,0-4,5	3,0	10,5-12,0	1,3	-	0,5	0,5	0,1	0,35	0,5
A413.0	GD-AlSi12	1,0	0,5	11,0-13,0	1,3	-	0,5	0,35	0,05	0,15	0,25

Tabla 2 Propiedades físicas y mecánicas de las materias primas. Fuente ^[13]  

Aleación ASM	Resistencia a Fluencia (MPa)	Resistencia máxima (MPa)	Elongación (%)
A360	165	320	3,5
A384.0	170	330	2,5
A413.0	130	290	3,5

Como se aprecia, todas las materias primas son aleaciones de aluminio al silicio y/o silicio-cobre, con pequeñas variaciones en su composición; específicamente la aleación A413, es una aleación con muy buena fluidez ya que se encuentra muy próxima al punto eutéctico, pero es la que presenta una ligera disminución del valor de fluencia y resistencia máxima; por lo que se decidió la comprobación del modelo geométrico, empleando MEF, a partir de la aleación A413.0, garantizando que, si la simulación del modelo propuesto resiste a los esfuerzos sometidos con esta aleación, también los resistirá con el resto de aleaciones comprendidas en las materias primas. De ser negativo el resultado, implicaría hacer modificaciones en las dimensiones de la pieza a obtener.

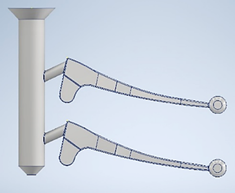
Para la comprobación de la pieza se utilizó la ayuda de un software gráfico el cual contiene en la base de datos el material seleccionado, figura 1.

Fuente: autores

Fig. 1 a) Pieza modelada, b) Pieza original. 

Para obtener valores cuantitativos de la carga real necesaria para accionar los mecanismos se realizó un experimento, donde se tomaron mediciones de las fuerzas necesarias para el accionamiento máximo en condiciones reales de funcionamiento, con ayuda de una Balanza de mano digital LCD 50 Kg, marca Electronic Scala; modelo portable; país de fabricación China (dinamómetro) con mínima capacidad en la medición de 5 g. Para el embrague se midió la fuerza necesaria para liberar todo el mecanismo y en el caso de la manilla de frenos, la fuerza necesaria para llegar a un frenado donde la velocidad de giro de la rueda fuera igual a 0 km/h con una fuerza aplicada en el radio exterior del neumático, equivalente al esfuerzo que recibe éste cuando van montados en la moto dos personas de 80 kg de peso.

En ambas manillas se realizaron mediciones tanto en el centro como en el extremo de las misma, condición de máximo esfuerzo.

La simulación se realizó empleando los valores en las condiciones más extremas a las que estará expuesta la manilla de freno durante su funcionamiento (accionamiento que demanda más carga). Estas serían cuando la manilla ha alcanzado su recorrido máximo (la leva que mueve a través del cable no puede girar más porque las zapatas están accionadas de forma máxima contra la tambora, como se muestra en la figura 2 y se sigue suministrando fuerza con la mano, y en el embrague cuando está completamente liberado y se sigue aplicando cierta fuerza. Para la simulación se empleó un valor de fuerza máxima de prensa que pueda aplicar un ser humano con su mano de 45 kgf (441 N), garantizando las condiciones de una frenada de pánico ^[14]. A su vez las condiciones iniciales para la simulación fueron: tipo de elemento tetraédrico, mínimo tamaño del elemento 0,2 mm, número máximo de refinados 10, criterio de parada 2 %, y umbral de refinado h de 0,75, todo lo anterior se tomó en cuenta para hacer un análisis de convergencia de la malla y donde se obtuvieron los valores de los esfuerzos equivalentes (Von - Mises).

Fuente: autores

Fig. 2 Mecanismo de freno de zapatas accionado por cable. (1) Tambor, (2) Zapatas, (3) Leva, (4) Cable 

Para el diseño del molde metálico se partió de un análisis de la pieza y se planteó una metodología similar a la brindada por Nath J ^[13], tal como se menciona a continuación.

1. Análisis de las características constructivas de la pieza.

2. Posición de la pieza en el molde y selección del plano de división.

3. Cálculo de las sobremedidas de maquinado.

4. Determinación de las inclinaciones de salidas.

5. Contracción de fundición.

6. Cálculo del sistema de alimentación.

7. Selección del material del molde.

8. Diseño del molde.

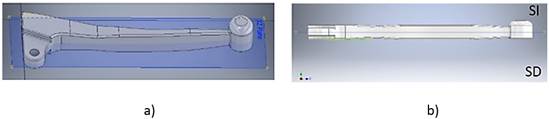
Se dividió la pieza en dos mitades, observando la marca de división de la pieza original, que nos brindó información sobre donde se encontraba el plano de división, y se propuso la división simétrica del semiproducto. Se presenta el plano de división de la pieza (en azul) en la figura 3; en la figura 3b se indican SI y SD como el semimolde izquierdo y derecho respectivamente, correspondientes a la posición vertical del molde.

Fuente: autores

Fig. 3 a) Plano de división en 3D, b) Plano de división sobre una superficie. 

Las contracciones y márgenes de maquinado se calcularon, partiendo del espesor promedio (s) y la composición de la aleación, con valor de contracción de 0,02 mm. En este caso lo único que se propuso a realizar por maquinado son los agujeros y el ranurado por donde pasa el cable, debido a que la relación diámetro longitud es muy pequeña y no se recomienda obtener por fundición. El resto de la pieza quedó tal cual sale de la fundición, aprovechando la alta precisión que garantiza la fundición en molde metálico, requiriendo solo un pulido a voluntad del cliente. Por tanto, no se hicieron modificaciones en las dimensiones de la pieza para crear la cavidad del molde.

Cálculo del sistema de alimentación (SA)

De igual forma, para realizar el cálculo del sistema de alimentación, se emplearon los criterios obtenidos de área de control Fc de la sección del tragadero en cm2, empleando las ecuaciones (1), (2) y (3):

(1)

(2)

(3)

Donde:

G	peso del metal fundido que pasa por el tragadero, kg
k e	velocidad específica de vertido, kg/s*cm3
V e	volumen espacial, cm3
t	tiempo de colada, s
S	coeficiente que está en función del espesor medio de la pieza
α y b	coeficientes que están en función del tipo de material a emplear, sus valores son 0,08; 0,15 respectivamente

Relación de las áreas para la colada

Para los moldes metálicos la relación entre las secciones de las diferentes partes del sistema de alimentación, alimentador (Fa), escoriador (Fe) y tragadero (Ft), se rige por la relación entre sus áreas. En este trabajo, por la configuración y facilidades de ubicación de la pieza en el molde, se prescinde del escoriador, por lo que solo se tomó la relación entre el tragadero y el alimentador según la relación publicada en ^[13, ^15]:

Fa: Ft = 1 : 1,2

Diseño de la Coquilla

Partiendo de los resultados de las expresiones anteriores se tomaron las dimensiones de los semiproductos que se deben obtener por fundición, los cuales reproducen la cavidad interior de la coquilla. En este caso se decidió colocar dos semiproductos dentro del molde, teniendo en cuenta las recomendaciones en ^[13] y las dimensiones del dispositivo mecánico porta molde existente y cuya posición del plano de división y para el vertido es vertical. En la figura 4 se observa el modelo de los semiproductos unidos por un sistema de alimentación común.

Fuente: autores

Fig. 4 Ensamble en 2D de los semiproductos en el sistema de alimentación.  

Selección del material de la coquilla

Para elaborar los moldes metálicos se emplean varios materiales: aceros herramentales, fundiciones grises, fundiciones maleables, fundiciones blancas, fundiciones nodulares, cobre, aluminio, siliconas, etc.; en dependencia del metal que se va a verter, del tiempo estimado que se quiere dure el molde, de las condiciones o facilidad para elaborarlo, etc., son algunos de los criterios que se emplean para la selección.

Según se expresa en la bibliografía ^[13], los moldes de hierro fundido pueden ser empleados para producciones de entre 10000 y 50000 piezas. Como nuestras necesidades de producción caen en este rango, se decidió emplear como material para el molde una fundición gris laminar disponible en el taller, que responde a las normas ASTM A-247 e ISO945-1975 (E); para introducir los valores de propiedades en los softwares de diseño y fundición. A líquido.

Consideraciones térmicas de la coquilla

El modelo propuesto para la simulación numérica de la solidificación de la colada se basa en la solución de la ecuación de Fourier-Kirchhoff según la ecuación (4):

(4)

Donde:

	es la eficiencia volumétrica de la fuente de calor interna, W/m^3
L	calor latente de solidificación, J/kg
T	temperatura, K
fs	fracción volumétrica de fase sólida, fs
C	Calor específico, J/(kgK)
λ	Coeficiente de conductividad térmica, W/(mK)
ρ	Densidad, kg/m^3
t	tiempo, s
x(x, y, z)	las coordenadas del vector de posición de un nodo considerado, m

Se ha supuesto que el frente de solidificación es difuso, por lo que las fuentes de calor internas no vienen evidentes en la ecuación de conductividad térmica y la ecuación (4) asume la forma de la ecuación (5).

(5)

El flujo de calor del frente de cristalización se gasta en calentar el molde de enfriamiento y se libera en el ambiente a través del borde de metal endurecido. Por lo tanto, podemos escribir la igualdad, ecuación (6).

(6)

Dónde:

КH	coeficiente de transferencia de calor para una pared plana, W/(m^2K)
Fsur = Fo	el área de superficie del molde de enfriamiento, m^2
𝑇P	temperatura de colada de la aleación, ºK
𝜌mo	densidad de la aleación y del material del molde, kg/m^3
Tsur,Tenv	la temperatura de la superficie exterior del molde y el medio ambiente, respectivamente, ºK
𝑐mo	capacidad calorífica del material del molde, J/(kgK)
T^0 mo	temperatura inicial de vertido, ºK
𝑇𝐶	temperatura de cristalización de la aleación, ºK
α3	el coeficiente de transferencia de calor desde la superficie exterior del molde de enfriamiento hasta el medio ambiente, W/(m^2K)

Partiendo de la ecuación (6) teniendo en cuenta la conductividad termica del metal y el molde se puede aplicar la ecuación (7):

(7)

Donde:

α1	el coeficiente de transferencia de calor en el frente de cristalización, W/(m^2K)
δmo	espesor de la capa de molde calentada, m]
λm , λmo	la conductividad térmica del metal y molde respectivamente, W/(mK)]
α2	se puede determinar a partir de las resistencias térmicas del espacio de gas y la capa de pintura.
δmo	es el espesor del borde de metal endurecido. [m]

Según Nath J ^[13], la variación de temperatura del metal líquido a través del espesor de pared del mismo, se asume muy pequeña debido a que la aleación de aluminio tiene elevada difusividad. La velocidad de trasnferencia de calor del metal al molde es proporcional a la diferencia de temperatura entre el metal y la superficie del molde (por la ley del enfriamiento de Newton). La velocidad de cambio de energía del metal es proporcional a la velocidad de trasnferencia de calor del molde (por la ley de conservación de la energía - primera ley de la terrmodinámica). La relación entre estas es expresada por la ecuación (8):

(8)

Donde:

tfs	tiempo de fluido, es el tiempo desde el comienzo del llenado de la cavidad hasta que la primera parte del metal alcanza la fracción sólida fs
Tdie, Tliq, Tsol, Te, Tgate	temperatura del molde, líquido, sólido, comienzo de solidificación y entrada respectivamente
ρ	densidad de la aleación [kg/m^3]
dW	promedio de espesor de pared de la fundición. [m]
cp	calor específico de la aleación. [J/(kgK)]
h	coeficiente global de transferencia de calor. W/(m^2K)

El coeficiente global de transferencia h se compone de dos elementos, relacionados por la ecuación 9:

1. coeficiente de transferencia superficial h_surf

2. coeficiente de transferencia convectivo h_c

El coeficiente global de transferencia de calor, se determina por la ecuación (9):

(9)

Si la temperatura del metal en la entrada está por debajo de la temperatura del líquido de la aleación, la solidificación comienza a partir de la temperatura de la entrada. Parte del calor latente se pierde parcialmente en este momento.

Si la temperatura del metal líquido está por encima de la temperatura del líquido de la aleación, la temperatura del inicio de solidificación Te, es la temperatura del líquido. Si el metal líquido está por debajo de la temperatura del líquido de la aleación, el inicio de la solidificación Te es la temperatura de la entrada.

La fundición por gravedad requiere tiempos diferentes en comparación con la fundición a presión. Como regla empírica, las velocidades de entrada pueden tomarse de entre 0,3 y 0,7 m/s para la fundición por gravedad, pudiendo ser algo mayores, pero nunca tan altas en comparación con los 25 a 70 m/s de la fundición a presión.

Resultados y Discusión

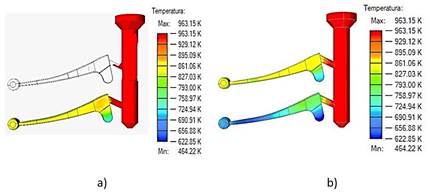
Después de la simulación en el Software disponible y con su análisis de convergencia correspondiente, se obtuvieron resultados satisfactorios con 56884 elementos y 91123 nodos. En la figura 5 se detallan los resultados de esfuerzos mecánicos y la zona crítica.

Fuente: autores

Fig. 5 Resultados de los esfuerzos, a) Ubicación de la fuerza, b) Zona donde se encuentra el mayor valor de los esfuerzos en la pieza modelada.  

Al comprobar, por el método de elementos finitos, la pieza que se desea construir con el material disponible de menor σf, 130 MPa, tabla 2, bajo las condiciones de esfuerzos máximos, 97,6 N/mm2, a las que estará sometida durante su funcionamiento, se obtuvo que, σf >σ1, demostrando esto que, es factible construirla con el material A413.0 y con otros materiales presentes en la empresa con valores mayores de resistencia; por lo que se decidió mantener el diseño y dimensiones originales de la pieza.

Otro resultado importante es el cálculo del tiempo de colada para determinar cada zona propuesta en el SA; resultando valores de un diámetro del tragadero de 24 mm y, según la relación propuesta, el diámetro del alimentador quedó en 10 mm aproximadamente. Se decidió por secciones circulares para el SA, ya que es la configuración más fácil de elaborar con equipos convencionales de maquinado.

Para determinar y comprobar las dimensiones de cada elemento e incluyendo el diseño del molde, se utilizó un software especializado en fundición, al cual se le introdujeron los valores calculados del SA y los obtenidos de las expresiones anteriores, permitiéndonos obtener resultados y compararlos con los resultados analíticos.

Simulación del llenado y solidificación de la pieza

las condiciones iniciales para ejecutar las simulaciones fueron: temperatura del molde, 150 ºC, temperatura del líquido, 770 ºC, tiempo de llenado, 10 s, altura de la cuchara del molde, 50 mm, molde sin inclinación, elemento tetragonal de 3,85 mm sin auto refinado, con un 50 % del compromiso entre rapidez y precisión.

El metal fundido fluyó desde el bebedero con flujo lineal hacia los alimentadores. Cuando el volumen de llenado llegó al 50 %, figura 6a, empezó a llenar de manera suave la mitad de la cavidad, desde la parte inferior hacia la parte superior de la otra pieza, figura 6b. Se observó una solidificación completa, con una correcta descripción del componente de fundición, mediante una solidificación progresiva.

Fuente: autores

Fig. 6 Esquema de temperatura de llenado, a) Llenado al 50 %, b) Llenado al 100 %.  

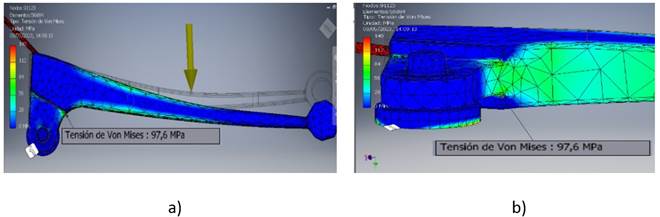
Ciertas partes de la fundición deben ser alimentadas por igual desde un bebedero o tubo(s) vertical(es) por metal líquido a medida que avanza el proceso de solidificación. En este caso es innecesario debido a que el rechupe queda fuera de la pieza, concentrándose en el alimentador, corroborando lo abordado en párrafos anteriores. El resultado se observa en la figura 8a, con un aumento en un 90 % para mejora su visualización. Otro de los aspectos analizados es la microporosidad, destacándose en estas simulaciones un 0 % como se muestra en la figura 8b. Este análisis es de gran importancia debido a que, cualquier vacío que quede dentro de la pieza compromete la resistencia de la misma, comportándose como un concentrador de tensiones. La predicción de la posibilidad de existencia de poros, criterio de Niyama ^[16], es otro criterio importante a valorar, el cual no reflejó problema alguno en esta probabilidad, figura 7c.

Fuente: autores

Fig. 7 Análisis de la solidificación, a) Posicion del rechupe debido a la contracción del metal, b) Posible microporosidad, c) Análisis de porosidad según el criterio de Niyama.  

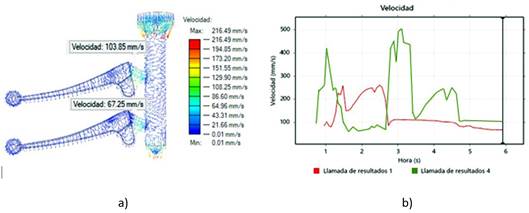
En el análisis de la simulación de flujo en el molde, tampoco se observó turbulencia durante el llenado, corroborado por los vectores de velocidad en la, figura 8a, además del comportamiento de la velocidad en las áreas de control en los gráficos de la figura 8b, estando entre los 67,25 mm/s y 103,85 mm/s corroborando un flujo no turbulento durante el llenado y a su ves que no hay atrapamiento de aire y enfriamiento disuelto, que provoque falsas soldaduras. Desde este punto de vista, nos hizo deducir que la propuesta del molde es satisfactoria.

Fuente: autores

Fig. 8 Análisis de la velocidad en las áreas de control, a) Vectores velocidad, b) Gráfico de velocidad vs tiempo de las sondas de a).  

En la figura 9, podemos apreciar las dos mitades del molde propuesto, modeladas en el software gráfico, donde se aprecian los orificios de las guías.

Fuente: autores

Fig. 9 Mitades del molde propuesto.  

Las dimensiones para las cuales se recomiendan emprender la fabricación del molde, según los resultados de las simulaciones, son: largo 247,4 mm, alto 176 mm, espesor 92,4 mm.

A través de varias simulaciones se lograron obtener valores de ciclos de trabajo de 45 segundos entre coladas, garantizando una velocidad de enfriamiento que permite mantener la temperatura del molde en el rango normal de trabajo para este tipo de proceso.

Conclusiones

De acuerdo con los resultados del comportamiento de la colada al inicio de la fundición, velocidad de flujo, evolución de la solidificación, microporosidad, porosidad y criterio de Niyama, se corroboró que tanto las dimensiones y diseño del molde, del SA y los valores iniciales de temperatura de trabajo y de vertido de la aleación, asegurará que las piezas no contengan defectos.

Las dimensiones propuestas para el molde, así como las condiciones de trabajo y de explotación propuestas, permiten mantener un flujo continuo de producción ininterrumpida.

Referencias

1.  Capuano G, Rimoli JJ. Smart finite elements: A novel machine learning application. Computer Methods in Applied Mechanics and Engineering. 2019;345:363-81. https://doi.org/10.1016/j.cma.2018.10.0461.

2.  Berselli G, Bilancia P, Luzi L. Project-based learning of advanced CAD/CAE tools in engineering education. International Journal on Interactive Design and Manufacturing (IJIDeM). 2020;14:1071-83. https://doi.org/10.1007/s12008-020-00687-42.

3.  Huang PH, Lin CJ. Computer-aided modeling and experimental verification of optimal gating system design for investment casting of precision rotor. The International Journal of Advanced Manufacturing Technology. 2015;79:997-1006. DOI 10.1007/s00170-015-6897-5

4.  Aravind S, Ragupathi P, Vignesh G. Numerical and experimental approach to eliminate defects in al alloy pump- crank case processed through gravity die casting route, Materials Today: Proceedings. 2020. https://doi.org/10.1016/j.matpr.2020.07.3654.

5.  Pinto HA, Silva FJ, Martinho RP, Pinto A G. Improvement and validation of Zamak die casting moulds. 29th International Conference on Flexible Automation and Intelligent Manufacturing (FAIM2019). Limerick, Ireland. Procedia Manufacturing. 2019;38:1547-1557. https://doi.org/10.1016/j.promfg.2020.01.1315.

6.  Patnaik L, Saravanan I, Kumar S. Die casting parameters and simulations for crankcase of automobile using MAGMAsoft, Materials Today: Proceedings. 2019. https://doi.org/10.1016/j.matpr.2019.08.2086.

7.  Zarbini Seydani M, Krimi A, Khelladi S, Bedel M, El Mansori M. 3D numerical simulation and experimental validation of resin-bonded sand gravity casting: Filling, cooling, and solidification with SPH and ProCAST approaches. Thermal Science and Engineering Progress. 2024;47: 102329 https://doi.org/10.1016/j.tsep.2023.1023297.

8.  Vergnano A, Brambilla E, Bonfiglioli G. Efficiency and Reliability of Gravity Die Casting Models for Simulation Based Design. In: Advances on Mechanics, Design Engineering and Manufacturing II. Lecture Notes in Mechanical Engineering. Springer, Cham;2019. https://doi.org/10.1007/978-3-030-12346-8_18.

9.  Taniguchi S, Maeda Y. Inlet Condition for Mold Filling Simulation in Gravity Casting of Aluminum Alloy. Materials Transactions. Japan Foundry Engineering Society. 2020;61(10):1981-1986. https://doi.org/10.2320/matertrans.F-M20208409.

10.  Dučić N, Jovičić A, Radiša R, Manasijević S, Slavković R, Radović D. Application of CAD/CAE/CAM Systems in Permanent-Mold Casting Improvement. Technical Gazette. 2020;27,6:2077-2082. https://doi.org/10.17559/TV-2019042215441010.

11.  Kholis AS, Achmad F, Yudianto A, Adiyasa IW, Solikin M, editors. Optimalisasi struktural pada handle kopling sepeda motor. Conference on Innovation and Application of Science and Technology (CIASTECH); 2020. https://v2.publishing-widyagama.ac.id/index.php/ciastech/article/viewFile/1981/138511.

12.  Prasetyono AP, Yudianto A, Adiyasa IW. Lightweight Design and Finite Element Analysis of Brake Lever for Motorcycle Application. ComTech: Computer, Mathematics and Engineering Applications. 2023;14(1):21-32. DOI: 10.21512/comtech.v14i1.8604

13.  Nath J. Aluminum Castings Engineering Guide. USA: ASM International; 2018.

14.  Guede Rojas F, Chirosa Ríos LJ, Vergara Ríos C, Fuentes Contreras J, Delgado Paredes F, Valderrama Campos MJ. Fuerza prensil de mano y su asociación con la edad, género y dominancia de extremidad superior en adultos mayores autovalentes insertos en la comunidad: Un estudio exploratorio. Revista médica de Chile. 2015;143(8):995-1000.

15.  Dučić N, Ćojbašić Ž, Manasijević S, Radiša R, Slavković R, Milićević I. Optimization of the gating system for sand casting using genetic algorithm. International Journal of Metalcasting. 2017;11:255-65. https://doi.org/10.1007/s40962-016-0040-815.

16.  Ivanina E, Monastyrskiy V, Ershov MY. Quantitative Estimation of Formation of Shrinkage Porosity by the Niyama Criterion. Inorganic Materials: Applied Research. 2022;13(1):100-5. DOI:10.1134/S2075113322010130

Recibido: 30 de Noviembre de 2023; Aprobado: 30 de Diciembre de 2023

^* Autor de correspondencia: [e-mail]

Los autores declaran que no existen conflictos de intereses

Victor M. Mir Labrada. Participó en la recopilación de datos e informaciones, en el diseño teórico y de investigación, tomadas de los informes técnico-productivos y Realizó contribuciones en el análisis e interpretación de los datos obtenidos, empleando los softwares en las diferentes etapas. Participó en la búsqueda de información, en el diseño teórico y de investigación, en la revisión crítica de su contenido, redacción y aprobación del trabajo final.

Tiel García Hernández. Realizó contribuciones en el análisis e interpretación de los datos. Participó en la búsqueda de información actualizada, en el diseño teórico y de investigación, en la recolección de los datos para la validación del trabajo, y en la revisión crítica de su contenido, redacción y aprobación del trabajo final.

Cristian L. Pérez López. Participó en la recopilación de datos e informaciones, en el diseño teórico y de investigación, procesamiento y valoración de resultados plasmados en el artículo, además de un análisis previo del proceso de fabricación. También tomó acciones con el uso de los softwares mencionados en el trabajo y participó en la búsqueda de información para el mismo, en la revisión crítica de su contenido, redacción y aprobación del trabajo final.

Alberto Menéndez Pérez. Trabajó en el diseño de la investigación, en la revisión de la investigación bibliográfica, en la recolección, procesamiento, análisis e interpretación de los datos y en el análisis de los resultados, así como, participó en la revisión crítica de su contenido, redacción y aprobación del trabajo final.

Yusleidi Cuesta Figueroa. Participo en la recolección de los datos y su ordenamienton, en la comprobación numérica de los resultados de los modelos, en la simulación para la validación del trabajo y en la revisión crítica de su contenido, redacción y aprobación del trabajo final.