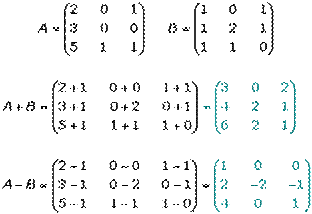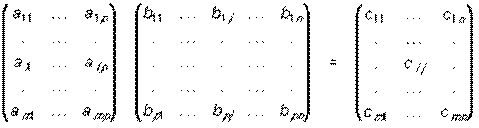Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Los siguientes principios de la matemática es una de las ciencias más antiguas. Los conocimientos matemáticos fueron adquiridos por los hombres, ya que no hay primeras etapas del desarrollo bajo la influencia, incluso de la más imperfecta actividad educativa. A medida que se iba complicando esta actividad, cambio y creció el conjunto de factores que influían en el desarrollo de las matemáticas, siendo este desarrollo observable a lo largo de toda su historia, la cual, contiene ejemplos que muestra como las matemáticas surgieron de la actividad productiva de los hombres.
La educación en las matemáticas siempre se ha considerado una formación compleja. En el presente trabajo se tratará de abarcar un espacio de reflexión y estudio sobre las matrices, en cuanto objeto de enseñanza y aprendizaje, y sobre los instrumentos conceptuales y metodológicos de índole general que la Didáctica de las Matemáticas en matrices está generando como campo de investigación.
Un material educativo multimedia según Chunga Chinguel (2015), son “aquellos recursos que han sido diseñado con el objetivo de facilitar los procesos de enseñanza aprendizaje, o con finalidad educativa”. Muchos maestros no encuentran material educativo interactivo que permita trabajar en la enseñanza de operaciones con matrices que contemple los métodos utilizados y los procesos de estas.
En matemática, una matriz “es un conjunto de números o expresiones dispuestos en forma rectangular. Formando filas y columnas. El orden o dimensión de una matriz se determina por el número de filas y columnas que componen” (Instituto Guatemalteco de Educación Radiofónica, 2016). Dado que puede definirse tanto la suma como el producto de matrices, en mayor generalidad, se dice que son elementos de un anillo. Una matriz se representa por medio de una letra mayúscula (A, B.…) y sus elementos con la misma letra en minúscula (a, b.…), con un doble subíndice donde el primero indica la fila y el segundo la columna a la que pertenece, se muestra la figura 1 (Vega, 2008).
En Matrices se pueden realizar varias operaciones como: suma, resta y multiplicación, ya sea con números enteros o fraccionarios, donde se obtiene un nuevo elemento a partir de dos elementos dados.
Para generar Suma y Resta de matrices de una misma dimensión, A=(aij) y B=(bij), se define la matriz suma como: A+B=(aij+bij). La matriz suma se obtiene sumando los elementos de las dos matrices que ocupan la misma posición. Se muestra en la figura 2.
Dadas dos matrices A y B podemos realizar su suma o diferencia de acuerdo a la siguiente regla. Para sumar o restar dos matrices del mismo tamaño, se suman o restan los elementos que se encuentren en la misma posición, resultando otra matriz de igual tamaño.
Por ejemplo: 2 13 −421 2x3 − 204 325 2x3 = 0 1 −1 −7 0 −4 2x3 Si las matrices tienen diferente tamaño, no se pueden sumar o restar entre sı.
Para poder sumar o restar matrices, éstas deben tener el mismo número de filas y de columnas. Es decir, si una matriz es de orden 3 ´ 2 y otra de 3 ´ 3, no se pueden sumar ni restar. Esto es así, ya que, tanto para la suma como para la resta, se suman o se restan los términos que ocupan el mismo lugar en las matrices (Fig 3).
Para sumar o restar más de dos matrices se procede igual. No necesariamente para poder sumar o restar matrices, éstas tienen que ser cuadradas. Se muestra en la Figura 4.
En la multiplicación de matrices “para obtener el producto de dos matrices, dichas matrices no necesariamente deben de ser iguales, es decir, no es requisito que tenga el mismo orden; En la operación de multiplicación se puede multiplicar dos matrices completamente diferentes”. (Segura Vásquez, 2014)
En el caso de producto de dos matrices, la primera debe tener el mismo número de columnas que filas la segunda. La matriz resultante del producto quedará con el mismo número de filas de la primera y con el mismo número de columnas de la segunda. Es decir, si tenemos una matriz 2 x 3 y la multiplicamos por otra de orden 3 x 5, la matriz resultante será de orden 2 x 5.
(2 x 3) x (3 x 5) = (2 x 5)
Se puede observar que el producto de matrices no cumple la propiedad conmutativa, ya que, en el ejemplo anterior, si multiplicamos la segunda por la primera, no podríamos efectuar la operación.
3 x 5 por 2 x 3,
Puesto que la primera matriz no tiene el mismo número de columnas que filas la segunda. Supongamos que A = (ai j) y B = (bi j) son matrices tales que el número de columnas de A coincide con el número de filas de B; es decir, A es una matriz m x p y B una matriz p x n. Entonces el producto AB es la matriz m x n cuya entrada i, j se obtiene multiplicando la fila i de A por la columna j de B (Figura 5).
Materiales y métodos
Durante la investigación se han hecho el empleo de diferentes métodos de carácter teórico, empíricos, estadísticos, de modelamiento y sistémicos, utilizando diferentes técnicas para el diagnóstico del estado de la problemática planteada.
En el estudio se aplicó una investigación bibliográfica o documental para distinguir y analizar los datos científicos para escribir el Marco Teórico y sustentación de las bases teóricas de autores Nacionales o Extranjeros.
Se realizó una investigación de campo observando las clases impartidas por los docentes del área de matemáticas a los estudiantes de la unidad educativa y poder obtener detalles que con otros tipos de investigaciones no se obtienen.
Resultados
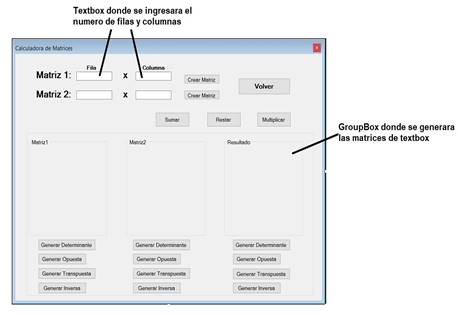
Se desarrolló un software educativo que simula todas las operaciones posibles de matrices matemáticas, simula una calculadora de matrices permitiendo alternar entre el número de elementos y el tipo de operación, además realizar observaciones cuando las operaciones se estén realizando con un método erróneo.
En el proceso enseñanza aprendizaje la calculadora de matrices explicará y resolverá el respectivo proceso al trabajar con matrices, en él se crean variables las cuales definen las filas y columnas de las matrices 1 y 2 en donde luego de un proceso en un groupbox se creará una matriz de textboxs dependiendo del valor ingresado en los respectivos espacios de las filas y columnas. Creada ya la matriz 1 y 2 se procede a llenar los textboxs de las matrices con los valores que se necesitará para continuar a poder desarrollar las operaciones que se programaron en botones y en un class program. (Garrido, et al., 2019). Se muestra en la Figura 6.
La Figura 7 muestra la calculadora de matrices donde se pondrán a calcular las operaciones básicas entre matrices y otras operaciones.
Formulario donde se realizarán las evaluaciones generándose operaciones aleatorias (Fig 8).
Formulario en el que se podrá observar los resultados de las evaluaciones realizadas por los usuarios (Fig 9).
Formulario menú tiene los botones para evaluar lo asimilado con el software o realizar diferentes tipos de operaciones con matrices.
En estos días existen muchos programas que nos permiten crear diversos trabajos para diferentes áreas, C#.net nos permite una mejor interacción en el manejo de la información, ya que es muy parecido al C++ y java, que son los mejores softwares para desarrollo de programas orientados a objetos existentes.
Software Educativo Interactivo que permitió simular operaciones con matrices, brindando ayuda constante para poder entender y comprender el proceso que se realiza para obtener un resultado. Con la aplicación del software se efectuó una mejora en el pensamiento lógico matemático de los estudiantes logrando un aprendizaje cognitivo (Guzmán, 2017).
Conclusiones
El uso del software ayudará a crear un algoritmo mental para la resolución de operaciones de Matrices, que para los estudiantes se torna un obstáculo a superarlo.
Los docentes del área de matemáticas con el uso del software lograron hacer más dinámica su clase y hará que los estudiantes estén a la expectativa de las diferentes rutinas y los procesos a seguir para la resolución de operaciones con matrices.
