DOI: http://dx.doi.org/10.13140/RG.2.2.26734.61764

 

ARTÍCULO ORIGINAL

 

Ajuste de los parámetros plásticos del modelo de Drucker Prager Extendido para la simulación de la respuesta mecánica de un suelo de textura arcillosa (Vertisol)

 

Adjustment of the plastic parameters of the Extended Drucker Prager model for the simulation of the mechanical response of a clayey soil (Vertisol)

 

 

Dr.C. Alain Ariel de la Rosa Andino,^I M.Sc. Patricio Rubén Alcocer Quinteros,^II Dr.C. Omar González Cueto,^III Dr.C. Alberto Masaguer Rodríguez,^IV Dr.C. Miguel Herrera Suárez,^V

^IUniversidad de Granma. Dpto. de Ciencias Técnicas, Bayamo, Granma, Cuba.
^IIUniversidad Técnica de Quevedo, Facultad de Ciencias de la Ingeniería, Quevedo, Ecuador.
^IIIUniversidad Central de Las Villas. Dpto. Mecanización Agropecuaria, Santa Clara, Villa Clara, Cuba.
^IVUniversidad Politécnica de Madrid, Escuela Técnica de Ingenieros Agrónomos, Departamento de Producción Agraria, Madrid. España.
^VUniversidad Técnica de Manabí, Departamento de Ingeniería Agrícola, Portoviejo, Manabí, Ecuador.

 

 

---

RESUMEN

El presente trabajo se realizó con el objetivo de ajustar los parámetros constitutivos del modelo de Drucker-Prager Extendido (DPE) que definen la fase de deformación plástica del suelo en la simulación de la respuesta mecánica de un suelo de textura arcillosa (Vertisol). La curva esfuerzo-deformación se dividió en dos partes y se buscaron dos ecuaciones que describen su trayectoria. Los datos iniciales se correspondieron con los datos determinados experimentalmente. A partir de estos se buscarán los valores aproximados tanto del ángulo de fricción interna del plano de falla del modelo de Drucker-Prager Extendido, así como, el ángulo de dilatancia. Finalmente se estimaron los valores óptimos de estos ángulos, disminuyendo los errores en las predicciones del modelo DPE por debajo del 4,35% haciéndolo adecuado para la simulación de la respuesta mecánica del suelo investigado.

Palabras clave: modelo constitutivo, deformación plástica, ajuste de curvas.

---

ABSTRACT

This research work was carried out with the aim of adjusting the constitutive parameters of the Extended Drucker-Prager (EDP) model which defines the phase of plastic deformation of soil in the simulation of the mechanical response of clayey soil (Vertisol). The stress-strain curve is divided into two parts and two equations describing its path were obtained. Initial data were consistent with the experimentally determined data. Starting from these results, the approximate values of both the internal friction angle of the fault plane of the Extended Drucker-Prager model, as well as the angle of dilatancy were searched out. Finally the optimum values of these angles were estimated, reducing errors in the predictions of the EDP model below 4.35% and turning this model adequate for simulating the mechanical response of the soil object of investigation.

Key words: constitutive model, plastic deformation, adjustment of curves.

---

 

 

INTRODUCCIÓN

El modelo constitutivo de Drucker-Prager Extendido ha sido ampliamente utilizado en investigaciones relacionadas con la simulación computacional de la respuesta mecánica de los suelos agrícolas, la interacción neumático-suelo y de la interacción suelo-apero de labranza (Xiang y Jin, 2004; Jafari et al., 2006; Davoudi et al., 2008; Herrera et al., 2008, 2013; Yu et al., 2008; Xia, 2011; González et al., 2012, 2013; Armin et al., 2014; Ibrahmi et al., 2014; Moslem y Hossein, 2014). Su utilización se debe fundamentalmente a que el mismo toma en cuenta las reglas de flujo, considerando que el suelo puede fluir de manera asociada o no asociada a la superficie de fluencia, además este modelo es capaz de predecir los cambios de tensiones producto de la deformación por ablandamiento o endurecimiento del suelo, apareciendo implementado en la mayoría de los software comerciales empleados en la simulación mediante el método de elementos finitos, necesitando solamente seis parámetros como datos de entrada, los cuales pueden ser determinados a través de los ensayos convencionales en laboratorios de mecánica de suelos.

Sin embargo, Egil y Risnes (2001); Xiang y Jin (2004); Helwany (2007),  Yin et al. (2009), SIMULIA (2008a) refieren que este modelo presenta una limitación o restricción a valores del ángulo de fricción menores de 22 grados, si la convexidad es asegurada. Esta limitación lo hace inconsistente para valores del ángulo de fricción mayores de 22 grados, a la hora de ajustar los parámetros de Drucker-Prager a los de Mohr-Coulomb lo que se reflejará en la exactitud de las predicciones. Por otro lado, Colmenares y Zoback (2002), Al-Ajmi y Zimmerman (2006), Herrera et al. (2008), Alejano y Bobet (2012), concluyeron, al comparar los datos experimentales con las predicciones, que el modelo de Drucker-Prager tiende a sobre predecir los esfuerzos desviadores. Otros investigadores como Otarawanna et al. (2004), Grujicic et al. (2009), reportan que la asunción de la regla de flujo asociada conlleva a excesiva dilatación ¹.

En Cuba ha sido utilizado por Herrera et al. (2008) en la simulación de la respuesta mecánica de un suelo arcilloso (Oxisol) ², en la modelación de la compactación provocada por el tráfico de neumáticos de los vehículos agrícolas sobre estos mismos suelos, encontrando ambos autores al modelo Drucker-Prager Extendido adecuado para simular estos fenómenos, aunque los errores en las predicciones oscilaron de 9,66 a 22,97% (Herrera et al., 2008) y de 9,6 a 19,15%  ² , según el nivel de humedad y densidad del suelo. Dichos autores refieren que el modelo presenta algunas imprecisiones al no poder representar la falla frágil del suelo y los cambios de tensiones. Al realizar un análisis usando el modelo Drucker-Prager en un suelo arenoso el ángulo de dilatancia tiene gran influencia en la predicción de los esfuerzos desviadores una vez que el suelo comienza a fluir plásticamente. Este efecto estará estrechamente relacionado a la densidad y al ángulo de fricción interna, pues estas propiedades guardan relación con la dilatancia. Para magnitudes superiores las predicciones no fueron buenas. Teniendo en cuenta lo expuesto anteriormente el presente trabajo tuvo como objetivoajustar los parámetros constitutivos del modelo de Drucker-Prager Extendido que definen la fase de deformación plástica del suelo durante la simulación de la respuesta mecánica de un suelo de textura arcillosa.

 

MATERIALES Y MÉTODOS

Modelo de Drucker-Prager Extendido

En esta investigación el suelo fue considerado como un material elastoplástico, por lo que criterio de fluencia utilizado fue el de Drucker-Prager lineal y se escribe como:

Donde: F= es la función de fluencia, t= los esfuerzos desviadores dados en por la ecuación (3), p= es el esfuerzo desviador dado en la ecuación (2), β=es el ángulo de fricción interna de Drucker-Prager y d= es la cohesión del material.

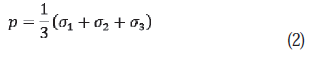
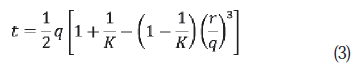
donde:

donde: K es el coeficiente que relaciona los esfuerzos desviadores obtenidos en compresión triaxial con los obtenidos en triaxial compresión (0,788 ≤ K ≤ 1); cuando K=1, entonces t=q, lo cual implica que la superficie de fluencia es el círculo de Von Mises representado en el plano de las tensiones desviadoras (Figura 1); r, es la tercera invariante de los esfuerzos desviadores y σ₁, σ₂ y σ₃ son las tensiones máximas, intermedias y mínimas, respectivamente. En el ensayo de compresión triaxial (σ ₂=σ₃).

El potencial de flujo plástico en el modelo de Drucker-Prager Extendido lineal se expresa como lo indica la ecuación (6).

donde:

G_f- es el potencial de flujo plástico,

ψ- ángulo de dilatancia en el plano p - t.

En el caso de materiales granulares como el suelo se aplica la regla de flujo no asociada ψ<β, el suelo no fluye en la dirección normal a la superficie de fluencia (Figura 2).

La regla de flujo asociada se aplica al establecer que ψ=β, donde el suelo fluye en dirección normal a la superficie de fluencia. Cuando el ángulo de dilatancia toma valor ψ=0, no hay deformación; sin embargo, si toma un valor mayor que cero ψ=0, el suelo se dilata.

Propiedades y parámetros del suelo requeridos por el modelo constitutivo de Drucker Prager Extendido

Las propiedades mecánicas y parámetros constitutivos requeridos como datos de entrada se tomaron de las investigaciones realizadas por de la Rosa et al. (2011), de la Rosa y Herrera (2013).

Implementación del modelo virtual

El procedimiento de la implementación del modelo en la herramienta computacional ABAQUS CAE 6.8-1 aparece descrito en la investigación realizada por de la Rosa et al. (2013). La simulación comprendió las nueve condiciones de humedad y densidad del suelo definidas durante la experimentación. En total se realizaron 54 simulaciones evaluando las diferentes configuraciones que puede tomar el modelo, considerando al suelo como un material dilatante (ψ=β) o no dilatante (ψ=0), tomando el coeficiente que relaciona los esfuerzos desviadores los siguientes valores K=0,80; K=calculado; K=1.

Método utilizado para el ajuste de los parámetros

Para el ajuste de los parámetros relacionados con la fase de deformación plástica del modelo constitutivo de Drucker-Prager Extendido, se utilizó el método de aproximación de funciones no lineales o de ajuste de curvas de Levenberg-Marquardt. Este es un método muy utilizado para la estimación de variables en diferentes campos estudios como por ejemplo en la estimación de la humedad del suelo de bosques tropicales (Truong-Loï et al., 2015). Levenberg (1944), Marquardt (1963), Moré (1978), refieren que este método de ajuste es realmente una combinación de dos métodos de minimización: el método de la pendiente del gradiente y el método de Gauss-Newton.

Como el ángulo del plano de falla de Drucker-Prager (β) domina la trayectoria de los esfuerzos desviadores una vez que el suelo comienza a deformarse plásticamente (Figura 3), desde la tensión de fluencia hasta la tensión de rotura. El ángulo de dilatancia (ψ) define la trayectoria de los esfuerzos desviadores una vez que el suelo alcanza la tensión de rotura.

La curva esfuerzo-deformación se dividió en dos partes y se buscaron ecuaciones que describen su trayectoria. Para el caso particular de este estudio el método fue programado en el software Matchad versión 14.0.

Los datos iniciales de estos dos parámetros se corresponden con los datos determinados experimentalmente. A partir de éstos se buscarán los valores aproximados tanto del ángulo de fricción interna del plano de falla del modelo de Drucker-Prager Extendido, así como, el ángulo de dilatancia.

El valor del coeficiente que afecta el ángulo de fricción de Drucker-Prager (β) está en función del tipo de falla que describa esta curva, como se aprecia en las ecuaciones 7 y 8.

Para falla plástica, donde se observó un punto de rotura bien definido y el suelo se deformó plásticamente por endurecimiento, la ecuación sería:

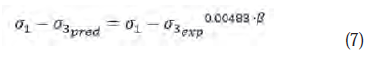
Para falla plástica, donde no se observó un punto de rotura bien definido y el suelo se deformó plásticamente por ablandamiento, la ecuación sería:

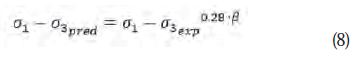
De igual forma se determinó el valor del ángulo de dilatancia (ψ) que satisface la exactitud en las predicciones. (ecuaciones 9 y 10).

Para falla plástica, donde se observó un punto de rotura bien definido y el suelo se deformo plásticamente por ablandamiento, la ecuación, sería:

Para falla plástica, donde no se observó un punto de rotura bien definido y el suelo se deformo plásticamente por endurecimiento, la ecuación, sería:

En la Figura 4, se muestra un ejemplo de la distribución aproximada de las funciones exponenciales dependientes del ángulo de fricción interna de Drucker Pragery dilatancia (ecuación 7, 8, 9 y 10); mostrando que en ambos casos se logra una adecuada aproximación de los valores predichos respecto a los experimentales, tanto para la falla plástica donde se observó un punto de rotura bien definido deformándose por ablandamiento, como para la falla plástica donde no se observó un punto de rotura bien definido, deformándose por endurecimiento.

 

RESULTADOS Y DISCUSIÓN

Ajuste de los parámetros plásticos del modelo de Drucker Prager Extendido

Para el caso del ángulo de fricción interna de Drucker-Prager se encontró una relación no lineal que permite correlacionar los valores del ángulo de fricción interna del suelo (ψ) con el ángulo estimado (β _est) a partir de la aproximación de funciones, redefiniendo la relación implementada en ABAQUS para relacionar los parámetros fricciónales del criterio de Drucker-Prager con los de Mohr-Coulomb. El gráfico del modelo ajustado se observa en la Figura 5a. Para el caso de del ángulo de dilatancia se obtuvo una relación polinomial, lo que permitió correlacionar los valores del ángulo de dilatancia (ψ _est) del modelo se puede observar en la Figura 5b. Ambos modelos son considerados moderadamente buenos, pues los valores del coeficiente de determinación oscilaron de 84,60 a 90,00% ².

Determinados los valores óptimos de los parámetros relacionados con la fase de deformación plástica del modelo Drucker-Prager Extendido, se pasó a la etapa de comprobación de las adecuaciones realizadas a los parámetros constitutivos del modelo de Drucker-Prager Extendido.

Para el caso donde el contenido de humedad estuvo cerca del límite plástico y el suelo exhibió una falla plástica con endurecimiento (Figura 6a), se aprecia que el modelo de Drucker-Prager Extendido, una vez realizada la adecuación de sus parámetros, es capaz de predecir con exactitud los esfuerzos desviadores tanto en la fase elástica como plástica, lográndose una disminución del error medio absoluto (EMA) de un 12,68 a 1,86%, (Tabla 1).

Cuando el contenido de humedad fue superior al límite de adherencia y el suelo mostró una falla plástica por ablandamiento (Figura 6b), se observó que el modelo es capaz de predecir la respuesta mecánica del suelo para todo el intervalo de deformación. De igual forma, que cuando el suelo exhibió una falla plástica por endurecimiento, se logró una disminución del error medio absoluto (EMA) de un 15,42 a 2,98%, (Tabla 1).

El menor valor del error se alcanzó cuando el contenido de humedad fue del 27% y la densidad de 1,05 g•cm^-3 (suelo seco y suelto), donde el suelo exhibió una falla plástica por endurecimiento. Por otro lado, el análisis estadístico mostró que no existen diferencias estadísticamente significativas entre las distribuciones experimentales y las predichas mediante la simulación (Tabla 1); pues el P_valor para los casos en estudio es P_valor ≥ 0,05.

 

CONCLUSIONES

-Se ajustaron los parámetros constitutivos del modelo de Drucker-Prager Extendido que definen la fricción y la dilatancia del suelo en la fase de deformación plástica logrando una reducción de los errores por debajo del 4,35%.

-El ajuste realizado a los parámetros constitutivos del modelo de Drucker-Prager Extendido mediante el método de aproximación de funciones de Levenberg-Marquardt posibilitaron predecir con exactitud la respuesta mecánica de Vertisol con independencia de su estado de humedad, densificación, así como del tipo de falla que exhiba.

 

NOTAS AL PIE

¹ GONZÁLEZ, C.O.: Modelación de la compactación provocada por el tráfico de neumáticos, de los vehículos agrícolas, en suelos en condiciones de laboratorio, Universidad Agraria de La Habana, Tesis presentada en opción al grado científico de Doctor en Ciencias Técnicas Agropecuarias, Mayabeque, Cuba, 123 p., 2011.

² CHACÓN, I.A.: Vis/NIR spectroscopic measurement of selected fertility parameters of Cuban agricultural soils, Faculteit Bio-ingenieurswetenschappe, Katholieke Universiteit Leuven, Tesis en opción al grado de Doctor in de Bio-ingenieurswetenschappen, 143 p., 2013.

 

BIBLIOGRAFÍA

AL-AJMI, A.M.; ZIMMERMAN, R.W.: “Stability analysis of vertical boreholes using the Mogi–Coulomb failure criterion”, International Journal of Rock Mechanics and Mining Sciences, 43(8): 1200-1211, diciembre de 2006, ISSN: 1365-1609, DOI: 10.1016/j.ijrmms.2006.04.001.

ALEJANO, L.R.; BOBET, A.: “Drucker–Prager Criterion”, [en línea], En: Ulusay, R. (ed.), The ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 2007-2014, Ed. Springer International Publishing, pp. 247-252, DOI: 10.1007/978-3-319-07713-0_22, 2012, ISBN: 978-3-319-07712-3, Disponible en: http://link.springer.com/chapter/10.1007/978-3-319-07713-0_22, [Consulta: 23 de mayo de 2016].

ARMIN, A.; FOTOUHI, R.; SZYSZKOWSKI, W.: “On the FE modeling of soil–blade interaction in tillage operations”, Finite Elements in Analysis and Design, 92: 1-11, diciembre de 2014, ISSN: 0168-874X, DOI: 10.1016/j.finel.2014.07.004.

COLMENARES, L.B.; ZOBACK, M.D.: “A statistical evaluation of intact rock failure criteria constrained by polyaxial test data for five different rocks”, International Journal of Rock Mechanics and Mining Sciences, 39(6): 695-729, septiembre de 2002, ISSN: 1365-1609, DOI: 10.1016/S1365-1609(02)00048-5.

DAVOUDI, S.; ALIMARDANI, R.; KEYHANI, A.; ATARNEJAD, R.: “A two dimensional finite element analysis of a plane tillage tool in soil using a non-linear elasto-plastic model”, American-Eurasian Journal of Agricultural & Environmental Sciences, 3(3): 498–505, 2008, ISSN: 1818-6769, 1990-4053.

DE LA ROSA, A.A.A.; HERRERA, S.M.; GONZÁLEZ, C.O.: “Propiedades macroestructurales de un Vertisuelo requeridas para la simulación computacional de la interacción suelo-apero de labranza mediante el Método de Elementos Finitos (MEF)”, Revista Ciencias Técnicas Agropecuarias, 20(2): 56-59, 2011, ISSN: 2071-0054.

DE LA ROSA, A.A.A.; HERRERA, S.M.; GONZÁLEZ, C.O.; BENÍTEZ, L.L.V.; CALZADA, P.I.; GARCÍA, P.L.: “Evaluación de la validez del modelo constitutivo Drucker Prager Extendido para la simulación de la respuesta mecánica de un Vertisol de la región central de Cuba”, Revista Ciencias Técnicas Agropecuarias, 22(1): 27-35, marzo de 2013, ISSN: 2071-0054.

DE LA ROSA, A.A.; HERRERA, S.C.: “Influencia del estado de humedad y densificación en las propiedades macroestructurales de un Vertisol en tres niveles de profundidad”, Revista de la Facultad de Agronomía, 30(1): 33-52, 2013, ISSN: 0378-7818.

EGIL, F.R.; RISNES, R.: “Application of Three Dimensional Failure Criteria on High-Porosity Chalk”, [en línea], En: Proceedings of the 6th Nordic Symposium on Petrophysics, Ed. Nordic Energy Research Programme-Norwegian U. of Science and Technology, Trondheim, Norway, pp. 15–16, 2001, Disponible en: http://www.ipt.ntnu.no/nordic/Papers/6th_Nordic_Flatebo.pdf, [Consulta: 23 de mayo de 2016].

GONZÁLEZ, C.O.; HERRERA, S.M.; IGLESIAS, C.C.E.; DIEGO, N.F.; URRIOLAGOITIA, S.G.; HERNÁNDEZ, G.L.H.: “Modelo en elementos finitos de la interacción neumático-suelo”, Revista Mexicana de Ciencias Agrícolas, (4): 664-671, 2012, ISSN: 2007-9230.

GONZÁLEZ, C.O.; IGLESIAS, C.C.E.; RECAREY, M.C.A.; URRIOLAGOITIA, S.G.; HERNÁNDEZ, G.L.H.; URRIOLAGOITIA, C.G.; HERRERA, S.M.: “Three dimensional finite element model of soil compaction caused by agricultural tire traffic”, Computers and Electronics in Agriculture, 99: 146-152, noviembre de 2013, ISSN: 0168-1699, DOI: 10.1016/j.compag.2013.08.026.

GRUJICIC, M.; HE, T.; PANDURANGAN, B.; BELL, W.C.; CHEESEMAN, B.A.; ROY, W.N.; SKAGGS, R.R.: “Development, parameterization, and validation of a visco-plastic material model for sand with different levels of water saturation”, Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials Design and Applications, 223(2): 63-81, 1 de abril de 2009, ISSN: 1464-4207, 2041-3076, DOI: 10.1243/14644207JMDA237.

HELWANY, S.: Applied Soil Mechanics with ABAQUS Applications, Ed. John Wiley & Sons, 402 p., 16 de marzo de 2007, ISBN: 978-0-471-79107-2.

HERRERA, S.M.; GONZÁLEZ, C.O.; NAVA, F.D.; RUIZ, V.J.; LÓPEZ, B.E.; IGLESIAS, C.C.E.: “Simulation of the soil mechanical behavior in the soil tillage tool interface”, Revista Facultad de Ingeniería Universidad de Antioquia, (69): 77-88, diciembre de 2013, ISSN: 0120-6230.

HERRERA, S.M.; IGLESIAS, C.C.E.; GONZÁLEZ, C.O.; LÓPEZ, B.E.; SÁNCHEZ, I.Á.: “Simulación mediante el Método de Elementos Finitos de la respuesta mecánica de un Oxisol”, Revista Ciencias Técnicas Agropecuarias, 17(2): 55–61, 2008, ISSN: 1010-2760, 2071-0054.

IBRAHMI, A.; BENTAHER, H.; MAALEJ, A.: “Soil-blade orientation effect on tillage forces determined by 3D finite element models”, Spanish Journal of Agricultural Research, 12(4): 941-951, 10 de octubre de 2014, ISSN: 2171-9292, DOI: 10.5424/sjar/2014124-5766.

JAFARI, R.; TAVAKOLI, T.; MINAEE, S.; RAOUFAT, M.H.: “Large deformation modeling in soil-tillage tool interaction using advanced 3D nonlinear finite element approach”, [en línea], En: Madureira, A.M. (ed.), 6th WSEAS International Conference on Simulation, Modelling and Optimization, Ed. World Scientific and Engineering Academy and Society, Lisbon, Portugal, p. 6, OCLC: 255720013, 2006, ISBN: 960-8457-53-X, Disponible en: http://www.wseas.us/e-library/conferences/2006lisbon/smo/index.htm, [Consulta: 1 de junio de 2016].

LEVENBERG, K.: “A method for the solution of certain non-linear problems in least squares”, Quarterly of Applied Mathematics, 2(2): 164-168, 1944, ISSN: 0033-569X.

MARQUARDT, D.W.: “An Algorithm for Least-Squares Estimation of Nonlinear Parameters”, Journal of the Society for Industrial and Applied Mathematics, 11(2): 431-441, junio de 1963, ISSN: 0368-4245, 2168-3484, DOI: 10.1137/0111030.

MORÉ, J.J.: “The Levenberg-Marquardt algorithm: Implementation and theory”, [en línea], En: Watson, G.A. (ed.), Numerical Analysis, ser. Lecture Notes in Mathematics, no. ser. 630, Ed. Springer Berlin Heidelberg, pp. 105-116, DOI: 10.1007/BFb0067700, 1978, ISBN: 978-3-540-08538-6, Disponible en: http://link.springer.com/chapter/10.1007/BFb0067700, [Consulta: 23 de mayo de 2016].

MOSLEM, N.; HOSSEIN, G.: “Numerical simulation of tire/soil interaction using a verified 3D finite element model”, Journal of Central South University, 21(2): 817-821, 21 de febrero de 2014, ISSN: 2095-2899, 2227-5223, DOI: 10.1007/s11771-014-2005-5.

OTARAWANNA, S.; MANONUKUL, A.; CARMAI, J.: “Modelling of metal powder compaction using the modified Drucker-Prager cap model”, [en línea], En: Proceedings of the 18 Mechanical Engineering Network of Thailand Conference, Ed. Department of  Mechanical Engineer Prince of Songkla University, Thailand, pp. 315–321, 2004, Disponible en: http://tsme.org/ME_NETT/ME_NETT18/fullpaper/amm/AMM52.pdf, [Consulta: 23 de mayo de 2016].

PTC: Mathcad, [en línea], (Versión 14.0), [Windows], Ed. Parametric Technology Corporation (PTC), United State of America, 2007, Disponible en: http://support.ptc.com/support/mathcad_downloads.htm.

SIMULIA: Abaqus Analysis User’s Manual. Version 6.8, [en línea], Ed. Dassault Systèmes Simulia Corp., vol. III, Providence, RI, USA, 647 p., 2008a, Disponible en: http://www.pdfdrive.net/abaqus-analysis-users-manual-vol3-e6117226.html, [Consulta: 7 de julio de 2016].

SIMULIA: Abaqus Theory Manual. Version 6.8, [en línea], Ed. Dassault Systèmes Simulia Corp., Providence, RI, USA, 1176 p., 2008b, Disponible en: http://130.149.89.49:2080/v6.8/books/hhp/default.htm?startat=pt02ch03.html, [Consulta: 7 de julio de 2016].

TRUONG-LOÏ, M.L.; SAATCHI, S.; JARUWATANADILOK, S.: “Soil Moisture Estimation Under Tropical Forests Using UHF Radar Polarimetry”, IEEE Transactions on Geoscience and Remote Sensing, 53(4): 1718-1727, abril de 2015, ISSN: 0196-2892, DOI: 10.1109/TGRS.2014.2346656.

XIA, K.: “Finite element modeling of tire/terrain interaction: Application to predicting soil compaction and tire mobility”, Journal of Terramechanics, 48(2): 113-123, abril de 2011, ISSN: 0022-4898, DOI: 10.1016/j.jterra.2010.05.001.

XIANG, R.Z.; JIN, C.W.: “Introduction to partly soil models in ABAQUS Software and their application to the geotechnical engineering”, Rock and Soil Mechanics, 25(S2): 144–148, 2004, ISSN: 1000-7598.

YIN, L.; KAU, S.; JIE, L.: “Aplication of Mohr-Coulomb equivalent area yield criterion to slope stability analusis”, Journal of Geodesy and Geodynamics, 29(1): 135-139, 2009, ISSN: 1671-5942.

YU, L.; LIU, J.; KONG, X.J.; HU, Y.: “Three-dimensional RITSS large displacement finite element method for penetration of foundations into soil”, Computers and Geotechnics, 35(3): 372-382, mayo de 2008, ISSN: 0266-352X, DOI: 10.1016/j.compgeo.2007.08.007.

 

 

Recibido: 27/11/2015
Aprobado: 03/06/2016

 

 

Alain Ariel de la Rosa Andino, Prof. Auxiliar, Universidad de Granma. Dpto. de Ciencias Técnicas, Bayamo, Granma. Email: [e-mail]