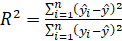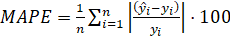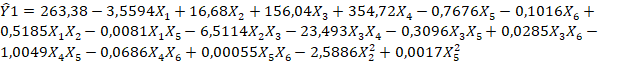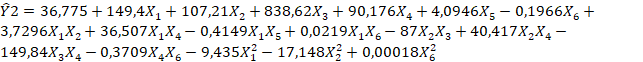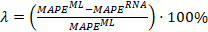Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
El pronóstico de consumo y demanda es un tema que ha sido ampliamente abordado en la literatura y continúa investigándose por la importancia en la operación de las redes y sistemas de potencia.
Para los sistemas de potencia, el pronóstico de la demanda máxima permite la toma de decisiones como la programación de la capacidad de generación, gestión del combustible, evaluaciones de seguridad y planificación de consumos y transacciones energéticas.
En los sistemas de potencia, bajo la concepción de redes eléctricas inteligentes, el volumen de información disponible debido a la gran cantidad de mediciones en varios puntos de la red, se ha incrementado y el pronóstico de la demanda está ganando mayor interés (Hernández, Baladrón, Aguiar, Carro, Sánchez-Esguevillas, Lloret & Massana, 2014).
Las técnicas de pronóstico se clasifican de acuerdo al horizonte de tiempo y al objetivo. La primera clasificación comprende: pronóstico de carga de muy corto tiempo (very short-term load forecasting (VSTLF); pronóstico de carga de corto tiempo (short-term load forecasting (STLF) y pronóstico de carga de mediano y largo tiempo (medium-term and long-term load forecasting (MTLF) y (LTLF), respectibly. VSTLF se refiere a intervalos de tiempo de segundos, minutos y horas y son generalmente utilizados para propósitos de control de flujo. STFL considera desde horas hasta semanas y se utiliza para ajustar la generación a la demanda. MTLF y LTLF se refieren a predicciones de la demanda con meses y años y son generalmente utilizados para la planificación de las redes.
La segunda clasificación se basa en la cantidad de datos para la predicción de la carga y se divide en dos grupos: los que utilizan solo un valor y los que utilizan múltiples valores para la predicción de la carga. Un ejemplo del primer grupo es el pronóstico de la demanda máxima para el próximo día. Otras clasificaciones se basan en las herramientas y modelos utilizados, por ejemplo modelos de pronóstico lineal y no lineal (Hernández, et al., 2014).
Los métodos lineales tienen limitaciones para capturar las no linealidades de las cargas y aunque actualmente se continuan utilizando, los modelos no lineales basados en redes neuronales artificiales (RNA), son los que mayormente se emplean. Desde hace más de un cuarto de siglo se utilizan exitosamente las redes neuronales para predecir carga y los investigadores han perfeccionado los modelos, obteniéndose mayor precisión aunque a costa de mayor complejidad.
Algunos investigadores han aplicado el análisis de componentes principales (PCA) para disminuir las variables de entrada y simplificar la arquitectura de las redes (Saravanan, Kannan, & Thangaraj, 2012, pp. 365-370), han empleado técnicas de minería de datos combinada con sistemas de inferencia neurodifusos (Motamedi, Zareipour, & Rosehart, 2012) o incluso la combinación de RNA con transformada wavelet o con sistemas neurodifusos para aumentar la exactitud (Hooshmand, Amooshahi, & Parastegari, 2013). Además, también se ha reportado el uso de redes secuenciales: una primera red neuronal para pronosticar las variables climatológicas, que serán utilizadas como entradas en la segunda red para el pronóstico de la demanda (Kulkarni, Simon, & Sundareswaran, 2013). Un acercamiento reciente a la solución de este tipo de problemas es la combinación de modelos individuales en un solo modelo (Xiao, Wang, Hou, & Wu, 2015); sin embargo, necesitan preselección de datos para eliminar interferencia entre ellos. También se han empleado otros métodos para seleccionar las entradas de las ANN usando coeficientes de correlación y distancia euclidiana (Ghofrani, Ghayekhloo, Arabali, & Ghayekhloo, 2015 ).
Un aspecto distintivo de los métodos de pronóstico es la consideración de la influencia de las variables climatológicas sobre el comportamiento de la carga. Aunque existe influencia del clima en la demanda de potencia (Honga, Wang & White, 2015; Ortiz Beviá, Ruiz de Elvira & Alvarez García, 2014), algunos investigadores no la consideran y modelan el consumo como series temporales exclusivamente (Xiao, et al., 2015; Ghofrani, et al., 2015).
La variable climática que se considera fundamentalmente es la temperatura, aunque algunos otros factores como la humedad relativa, velocidad del viento, y nubosidad pueden ser introducidas en el modelo para mejorar la calidad de la predicción (Hooshmand, et al., 2013; Kulkarn, et al., 2013; Honga, et al., 2015; Ortiz, et al., 2014; Badri, Ameli & Birjandi, 2012; Berardino & Nwankpa, 2013; Bagnasco, Saviozzi, Silvestro, Vinci, Grillo & Zennaro, 2014).
Debido a que la demanda de potencia es claramente dependiente del sector (industrial, comercial, residencial, administrativo, etc), la influencia de las variables climatológicas pueden ser más relevantes si las cargas de aire acondicionado o calefacción son predominantes. Se han desarrollado modelos para regiones pequeñas que no consideran el clima (Hernández, et al., 2014), pero se reconoce que para trabajos futuros debe ser incluido.
Ahora bien, pronosticar la demanda en edificios públicos es un tema que se ha trabajado en menor medida. Para los edificios públicos, pronosticar la demanda de potencia es de gran importancia dentro de la gestión energética, sobre todo para la actividad de planificación.
Las instituciones destinadas a la educación y los servicios se consideran parte del sector público, que está conformado por las ramas del comercio y de los servicios. Este sector consume alrededor del 3% de la energía que se consume en Cuba y la tendencia es a crecer debido a factores como crecimiento del turismo, recuperación de la actividad industrial, recuperación de hospitales e instituciones de salud, etc. En el caso específico del consumo de energía en las instituciones del MES y del MINED, se incrementa debido a la introducción sistemática de nuevo equipamiento, como computadoras, televisores y sistemas de climatización
El consumo de energía eléctrica en instituciones dedicadas a la educación y los servicios se diferencia, por su magnitud, del de las empresas industriales, las que presentan un valor considerablemente mayor. No obstante, a nivel global, el consumo de energía en edificios públicos tiene un peso alto en la estructura de consumo.
Para el caso de las universidades e instituciones educacionales, es necesario el estudio y determinación de indicadores confiables en el uso de la energía eléctrica como uno de los pasos fundamentales en el establecimiento de sistemas de monitoreo y control de la energía.
Los modelos de consumo que se establecen como línea base energética, y que permiten establecer Indicadores de Desempeño Energético (EnPIs, por sus siglas en inglés) para los sistemas de gestión de la energía, también se utilizan, entre otras cosas, para planificar consumos en función de planes productivos u otras variables. En este sentido constituyen modelos de pronósticos y si se emplean con este fin, permiten a la empresa o entidad de servicios anticiparse a los sobreconsumos y tomar medidas para evitarlos.
Pronosticar el consumo o la demanda de electricidad puede proveer de información aplicable para la evaluación del desempeño energético dentro de la instalación y para propósitos de mejora de la eficiencia en el uso de la energía, particularmente cuando se consideran sistemas de distribución a media y baja tensión, como es el caso de un campus universitario.
Hoy día, las instituciones universitarias son cada vez más conscientes de su realidad competitiva y sobre todo de la importancia de mantenerse vigentes y actualizadas en el nuevo mundo globalizado. Igualmente, son más responsables de su misión en la sociedad, deseando lograr la permanencia a través de la calidad formativa, medida a través de sus diferentes frentes. Las anteriores situaciones llevan, como en cualquier contexto empresarial, a la racionalización en los gastos de operación con respecto a los ingresos que se logran por diferentes conceptos, y uno de los gastos a considerar son los energéticos.
Los modelos de pronóstico son también herramientas ventajosas desde el punto de vista económico. De hecho, pueden aportar información valiosa para detectar tempranamente oportunidades y riesgos asociados al uso de la energía. La tendencia en el mercado energético mundial con paradigmas basados en conceptos de redes inteligentes, requiere mejores políticas de gestión de la carga y pronósticos más confiables, tanto para usuarios individuales como a escala del sistema de potencia. La posibilidad de insertar fuentes renovables de energía en el sector empresarial y de servicios necesita modelos que permitan coordinar las incertidumbres propias de estas fuentes con la demanda de la carga.
Todos estos aspectos anteriormente señalados pueden ser considerados también, en mayor o menor magnitud, si el ambiente de trabajo es una institución de educación superior con su campus universitario, aunque en la literatura científica revisada se reportan pocos trabajos acerca de la predicción de carga en las universidades y su empleo en los sistemas de gestión energética. Por ejemplo, Fernández desarrolló un modelo para el pronóstico a mediano plazo que emplea modelos ARIMA y RNA (Fernández, 2007). Se publicó un trabajo de pronóstico de carga para una facilidad de media tensión de un gran hospital universitario localizado en Roma, Italia (Bagnasco, et al., 2014). En esa investigación emplea una RNA perceptron multicapas para el modelo, lo que reduce el error del pronóstico; pero el método resulta complejo al tener que trabajar con cuatro redes neuronales y requerir mucha información. Basado en este trabajo, se desarrolló un modelo para la Universidad de Sao Paulo, Brasil, con una metodología más simple que puede ser integrada a los sistemas de gestión energética (Gómez Sarduy, Gregio di Santo & Saidel, 2016)
Precisamente en las universidades existen patrones de consumo determinados por el equipamiento existente, la cantidad de estudiantes, el número de estudiantes internos y de ellos cuántos son becarios extranjeros. Otras variables que influyen en el consumo son de carácter temporal e incluyen épocas de exámenes, vacaciones, feriados y otras actividades. Sin embargo, los estudios de este tipo realizados hasta el momento en Cuba no se enfocan a pronosticar con tiempo suficiente la demanda, sino más bien a la búsqueda de indicadores de desempeño energético. Como ejemplo se puede mencionar en la Universidad de Cienfuegos los estudios de Fernández (2007); González (2015); Ortíz (2016).
En la Universidad de Cienfuegos, en el Centro de Estudios de Energía y Medio Ambiente (CEEMA), se ha generado gran parte del arsenal tecnológico para la gestión eficiente de la energía en las universidades y sus sedes. También en esta universidad se ha trabajado desde hace varios años en el pronóstico de la energía consumida mensualmente para su incorporación al sistema de gestión energética.
La Universidad de Cienfuegos es un centro de Educación Superior (CES) con dos sedes en la Ciudad de Cienfuegos. La sede “Carlos Rafael Rodríguez”, es la sede central donde se encuentra el rectorado y además las facultades de Ingeniería, Ciencias Económicas y Empresariales, Estudios Socioculturales y Educación Física. Dentro de los indicadores de desempeño energético que le miden a la institución, se encuentra la estructura de consumo en el pico. Esto no es más que el porcentaje que del consumo total diario representa el consumo durante el horario de máxima demanda del sistema y debe ser igual o menor a 16%, según requerimientos de la política trazada por la Oficina Nacional de Uso Racional de la Energía (ONURE). Cuando es superior, se incumple con este indicador y se deben explicar las causas. En esta institución, un análisis de la estructura de consumo reveló que, en el año 2016, un 60% de los días se superó el 16% del consumo del día durante el pico.
Los análisis de incumplimientos en la estructura de consumo establecida por la ONURE tienen un carácter puramente forense. Lo correcto sería poder anticiparse a este consumo 24 horas antes y tomar las medidas necesarias para que no suceda. Para hacer esto se necesita un modelo de pronóstico confiable que considere variables temporales y que tenga en cuenta la historia anterior al evento que se quiere predecir. Esto precisamente es el centro de esta investigación, cuyo objetivo es establecer el pronóstico de consumo para cada horario de la tarifa, de manera que se pueda estimar anticipadamente el porcentaje que representará el consumo pico del total diario y en caso de que esta predicción supere el 16% establecido, tomar las medidas pertinentes para no excederse.
Desarrollo
La obtención de un modelo adecuado para el consumo de energía en el periodo de máxima demanda, como cualquier otro proceso de modelación, involucra un compromiso entre precisión y complejidad. La mayor precisión se obtiene añadiendo complejidad al modelo, mientras que modelos más sencillos generalmente conducen a resultados menos precisos. Por esta razón, en esta investigación se propone explorar el comportamiento de modelos lineales y no lineales desarrollados para predecir la energía consumida durante el pico.
De acuerdo a la literatura esta investigación se caracteriza por Hernández et al. (2014):
Modelos: lineales y no lineales.
Area: campus Universidad de Cienfuegos, sede central.
Horizonte de pronóstico: STLF.
Objetivo: varios valores (consumo horario pico y consumo resto del dia).
Variables: carga electrica con datos temporales.
La metodología comprende tres pasos: recolección de información, preprocesamiento de los datos y desarrollo de los modelos de pronóstico.
Inicialmente, se recogen los datos históricos (paso 1) y seguidamente se tratan antes de utilizarlos para la modelación (paso 2). Este tratamiento incluye el agrupamiento, conversión y filtrado y creación de nuevas variables para los tipos de dias y variables temporales. Posteriormente se desarrollan los diferentes modelos (paso 3), correlacionando los datos seleccionados (variables dependientes como día, mes y tipo de día, consumos 24 horas antes como datos de entrada y el consumo de energía del día y del pico como variables de salida). Para ello se utilizan funciones disponibles en el toolbox del Matlab.
Modelos lineales y no lineales
Los métodos de regresión para pronósticos de consumo de energía a corto plazo han sido ampliamente utilizados desde hace más de 30 años (Mirowski, Chen, Ho & Yu, 2014). Debido a que el consumo de energía de la universidad es función de varias variables, los modelos de regresión lineal múltiple (MLR) son más apropiados que la regresión lineal simple.
De esta manera, se puede modelar el consumo de potencia como una combinación lineal de variables relacionadas con el día de la semana, tipo de día, mes, etc. La comprensión e interpretación de este modelo es fácil y no requiere de un software especializado para su evaluación. Este tipo de modelo matemático provee una formulación global y explícita del comportamiento de la carga.
Aunque el consumo de energía se obtiene con facilidad de las lecturas de los metros contadores, su valor es conocido solamente cuando se ha consumido y no antes. El conocimiento previo de este consumo solamente es posible mediante la predicción a partir de modelos de consumo. La precisión del pronóstico de consumo es de gran valor para los sistemas de gestión energética. Basado en la literatura consultada, las RNA son una alternativa a los métodos estadísticos clásicos en términos de precisión de los resultados pronosticados (Hernández, et al., 2014).
Los modelos no lineales basados en RNA para la predicción han ganado mayor atención desde la segunda mitad de los 80 (Hernández, et al., 2014). Su capacidad de aprendizaje de la experiencia, capacidad de generalización a nuevos casos y su capacidad para encontrar relaciones complejas y no lineales entre variables de entrada y salida, mediante un proceso conocido como entrenamiento con datos históricos, hacen a las RNA atractivas para modelos de pronóstico de carga. La diferencia fundamental entre los modelos no lineales y lineales es que los primeros no requieren una representación matemática clara para representar la dependencia entre diferentes parámetros para resolver un problema, lo cual ahorra tiempo; mientras los modelos lineales requieren una definición precisa mediante ecuaciones.
Una red neuronal, es un sistema de procesadores paralelos conectados entre sí. Varias neuronas conectadas en paralelo forman una capa y varias capas conectadas en serie forman la red. Esquemáticamente cada uno de sus elementos de procesamiento (neuronas) se representan como un nodo. Estas conexiones establecen una estructura jerárquica que tratando de emular la fisiología del cerebro busca nuevos modelos de procesamiento para solucionar problemas concretos del mundo real.
Una vez desarrollados los modelos se necesita analizar su exactitud. Una medida de la misma se define a menudo en términos del error en el ajuste, que es la diferencia entre el valor estimado por el modelo y el valor real. Entre las medidas de exactitud más utilizadas están: el coeficiente de correlación (R2) y el porcentaje de error absoluto medio (MAPE).
El coeficiente de correlación (ecuación 1) se calcula como:
Ecuación 1
Donde: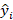 
es el valor estimado por el modelo, 
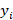es el valor real, 
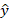es el valor medio y n es el número de observaciones de la muestra.
El porcentaje de error absoluto medio es un parámetro estadístico que da una idea global de la diferencia entre la predicción y el valor real y se calcula como se muestra en la ecuación 2:
Ecuación 2
Adquisición y procesamiento de datos
Comoquiera que el objetivo del trabajo es encontrar un modelo para el pronóstico a corto plazo del consumo de energía por horario de la tarifa y determinar con 24 h de antelación si el consumo del horario pico excederá el 16% del consumo total del día, de manera que se puedan tomar las medidas necesarias para su mitigación, entonces es necesario conocer estos consumos históricos para un periodo base y utilizarlos para desarrollar el modelo de pronóstico.
Para desarrollar este modelo, la información se obtuvo de la base de datos que contiene lecturas diarias del metro contador para cada horario de la tarifa. Esto permite disponer de los datos de consumo diario para el horario de madrugada, día y pico. Las variables temporales son las correspondientes al mes y al día. De esta manera se tienen las siguientes variables:
Mes: indica el mes del año con valores de 1 a 12
Día: indica el día de la semana desde 1 a 7, siendo 1 para el domingo y 7 para el sábado
Consumo total y consumo pico: son los consumos de energía en kWh para todo el día y durante el pico.
El procesamiento de los datos comienza con un análisis de clusterización para determinar si existen datos que se puedan agrupar en función del tipo de día o de algún periodo específico o que sigan un patrón estacional.
Los grupos se determinan utilizando la técnica de clusterización k-Means y se considera que los datos de consumo diario pueden ser segmentados en dos clústeres de datos. El primero de estos dos grandes grupos se corresponde con fines de semana, periodo vacacional, final y comienzo del curso académico y otros días de actividad reducida, mientras el segundo se corresponde con los días de actividad normal. Por esta razón se establece una nueva variable, denominada Día-Tipo. A esta variable se le asignará valor cero para días de actividad reducida y valor uno para días normales.
Modelo lineal
Para el caso que interesa en esta investigación, se necesita obtener un modelo para el consumo pico y otro modelo para el consumo total, con el objetivo de estimar la estructura de consumo en el horario de máxima demanda.
Como primer paso, se construyó la matriz de variables de entrada o predictores. Esta matriz tiene la siguiente estructura: X = [X 1 X 2 X 3 X 4 X 5 X 6 ].
Cada columna representa una variable considerada en el modelo, las cuales son:
X 1 : mes del año con valores de 1 a 12
X 2 : día de la semana, 1 para el domingo y 7 para el sábado
X 3 : 0 para día de poca actividad (incluye fines de semana, vacaciones, feriados y otros) y 1 para día de actividad normal
X 4 : es el tipo de día 24 horas antes del pronóstico
X 5 : es el consumo de energía en el horario pico el día antes del pronóstico, en kWh.
X 6 : es el consumo de energía del día antes del pronóstico, en kWh.
Para el caso de las variables de salida, estos son dos vectores que contienen los valores del consumo de energía en el horario pico Ŷ1 (ecuación 3) y del consumo de energía total del día Ŷ2 (ecuación 4).
Los resultados del ajuste para el modelo de consumo pico están dados por la ecuación 3:
Ecuación 3
El coeficiente de correlación R2 ajustado es 0,831 y la raíz del error medio cuadrático es 28,5 kWh.
Para verificar la bondad del ajuste, se grafican en un mismo plano los valores reales del consumo pico y los estimados por el modelo. El modelo obtenido sigue con bastante exactitud el perfil de consumo pico real. No obstante, se calcula el coeficiente de correlación entre ambas magnitudes (real y estimado) como una medida de exactitud, cuyo valor es R2=0,839 calculado según ecuación 1. Para este modelo, el MAPE, calculado por la ecuación 2 es 11,97%.
Para el consumo total, los resultados se ajustan a la expresión:
Ecuación 4
El coeficiente de correlación R2 ajustado, es 0,751 y la raíz del error medio cuadrático es 219 kWh.
De igual manera el valor real y estimado del consumo total del día se corresponden con bastante similitud con coeficiente de correlación R2=0,7618 y el MAPE es de 10,72 %.
Modelo con RNA
El modelo de red neuronal se desarrolló en ambiente Matlab. Los datos contienen 365 muestras correspondientes a cada día del año 2016 tomado como base, de los cuales 60% son usados para entrenamiento, 20% para validación y 20% para prueba.
Para el diseño de la red se adopta una configuración de dos capas ocultas y una capa de salida. La arquitectura es 10 neuronas en la primera capa, 10 en la segunda y 2 en la tercera.
El valor de R2 que se obtiene con esta red durante el entrenamiento es de 0,939. Este valor estadístico nos indica la capacidad de generalización de la red y es el coeficiente de correlación entre los valores del consumo pico y total resultantes del modelo y los valores de consumo pico y total medidos. Este coeficiente de correlación significa la fidelidad para reproducir el comportamiento de un objeto o proceso simulado.
El MAPE para los modelos con RNA, calculado según la ecuación (2) para el consumo pico es de 10,32% y para el consumo total es de 8,033%.
Comparación entre modelos
Los tipos de modelos obtenidos se comparan considerando el valor del porcentaje de error absoluto medio (MAPE), siendo el modelo no lineal el que tiene un mejor comportamiento de acuerdo a este parámetro.
Para una mejor comparación de los modelos desde el punto de vista cuantitativo, se define el porcentaje de mejora en (Hao, Dipti, & Abbas, 2014).
Este porcentaje de mejora se denomina λ y se determina mediante la ecuación 5 como:
Ecuación 5
Donde: MAPEML es el porcentaje de error absoluto medio del modelo lineal y MAPERNA es el porcentaje de error absoluto medio del modelo neuronal a comparar.
El porcentaje de mejora del modelo neuronal con relación al modelo lineal, para el pronóstico del consumo pico y para el pronóstico del consumo total es de λcons-pico = 13,78% y λcons-total = 25,07%, respectivamente.
Conclusiones
En la Universidad de Cienfuegos existe un sistema de gestión establecido, pero no contempla la predicción del consumo en el horario pico y, por lo tanto, carece de las herramientas para tomar las medidas necesarias de manera anticipada que eviten sobreconsumos en este horario y excesos en la estructura de consumo del pico.
La literatura consultada refiere que existen diversos modelos de pronóstico en función de las variables a pronosticar y el periodo de tiempo que abarca el pronóstico. Sin embargo, son escasos los reportes referidos al pronóstico energético en instituciones de educación superior o campus universitarios. La tendencia actual es a emplear modelos no lineales basados en RNA, fundamentalmente.
Los métodos de regresión para pronósticos de consumo de energía a corto plazo, han sido ampliamente utilizados, por ser más sencillos y definir una expresión matemática que puede ser evaluada fácilmente sin softwares especializados. Sin embargo, los modelos basados en RNA (modelos no lineales) para la predicción han ganado mayor atención debido a su capacidad de aprendizaje, capacidad de generalización y su capacidad para encontrar relaciones complejas y no lineales entre variables de entrada y salida.
Para el procesamiento de los datos se consideró una nueva variable que caracteriza la actividad del día, como resultado de aplicar el algoritmo de clusterización k-Means para el agrupamiento. Los tipos de días clasificados son: días de poca actividad (incluyen viernes, sábado y domingo, días feriados y periodo de vacaciones) y días de actividad normal.
Se desarrollaron modelos de regresión lineal múltiple para el consumo pico y para el consumo total del día, que correlacionan variables temporales y de consumo energético del día previo al pronóstico con el consumo pico y total. El porcentaje de error absoluto medio (MAPE) para ambos modelos es 11,97% y 10,72% respectivamente.
Se desarrolló una red neuronal de tres capas y arquitectura 10-10-2. El porcentaje de error absoluto medio (MAPE) de este modelo para el año 2016 es de 10,32% y 8,033% para el consumo pico y para el consumo total respectivamente. El modelo neuronal supera al lineal en un 13,78% para el consumo pico y en un 25,07% para el consumo total.
El modelo de pronóstico obtenido puede ser incorporado como una herramienta al sistema de gestión energética de la universidad, ya que permite estimar con 24 horas de anticipación el consumo de energía del día y del horario de máxima demanda y por lo tanto, estimar la estructura de consumo del pico y tomar las medidas necesarias para evitar su exceso.
