INTRODUCCIÓN
El agua es el factor que limita la producción en muchas partes del mundo donde las precipitaciones no son abundantes. Con los incrementos recientes en las demandas de productos agrícolas y las sucesivas crisis alimentarias en los países subdesarrollados, la necesidad de mejorar el uso del agua en la agricultura es una prioridad (Raes et al. (2018). Como parte de sus esfuerzos hacia estos objetivos, Steduto et al. (2009) desarrollaron el modelo llamado AquaCrop y lo definen como el modelo agronómico de la FAO, diseñado para: simular la biomasa de varios tipos de cultivos herbáceos en respuesta al uso del agua y el rendimiento agrícola esperado en función de una menor disponibilidad de agua, en un determinado ambiente y en una región particular.
El modelo AquaCrop ha sido evaluado por varios autores. Abedinpour et al. (2012) evaluaron el modelo en el cultivo del maíz en condiciones semiáridas y encontraron valores satisfactorios para los indicadores evaluados. Abi et al. (2014) encontraron exactitud entre los valores simulados y observados, en los cultivos de soya y girasol para diferentes épocas de siembra y regímenes hídricos. Amiri et al. (2014); Andarzian et al. (2011); Anjum et al. (2014) al evaluar la cobertura foliar en los cultivos de arroz y trigo, también encontraron evaluaciones satisfactorias.
En Cuba hay pocos trabajos publicados sobre el uso de AquaCrop, encontrándose los resultados de González et al. (2018), quienes evaluaron la capacidad predictiva del modelo bajo la condición de estrés hídrico en el cultivo de sorgo en suelo Ferralítico Rojo. Los resultados obtenidos por los autores antes citado, demostraron que las predicciones del rendimiento del grano, el estrés hídrico y la cobertura foliar, fueron buenas. También se reportan los resultados de Tornés et al. (2016), quienes demostraron la capacidad de este modelo simular de forma satisfactoria las variables: cobertura foliar, biomasa seca aérea y contenido total de humedad.
Uno de los cultivos priorizados en nuestro país es el frijol (Phaseolus vulgaris L.), durante su producción se presentan problemas de: variabilidad climática (déficit de precipitaciones y aumentos de temperatura), incidencia de plagas y enfermedades, uso del agua de riego, entre otros. Debido a lo anterior es necesario que el país pueda disponer de herramientas que le sirvan de ayuda a la toma de decisiones para lograr el menor costo económico y ambiental. El trabajo tiene como objetivo evaluar la exactitud del modelo AquaCrop en la simulación del rendimiento del cultivo del frijol común en condiciones variables de disponibilidad hídrica y población.
MATERIALES Y MÉTODOS
Localización
La investigación se desarrolló desde enero hasta abril del año 2017. El área de investigación pertenece a la Cooperativa de Créditos y Servicios (CCS) Clemente Ramos, municipio Bayamo, provincia Granma, la cual se encuentra ubicada a los 20° 22' 57,1" de Latitud N y a 76° 38' 16,4" Longitud O con una altura de 52,50 msnm.
Características del suelo
El suelo se clasificó como del tipo Vertisol pélico y del subtipo Vertisol pélico calcico según la Clasificación Genética de los Suelos de Cuba (Hernández et al., 2015). La profundidad efectiva es de 50 cm por lo que clasifica como poco profundo, de pendiente llana. Con la relación a la textura predomina la arcilla montmorillonita (> 75 %). El contenido de humedad a la capacidad de campo es equivalente al 43 % mss. El punto de marchitez permanente se determinó mediante el uso de la fórmula empírica la cual se deriva de conocer el valor de la capacidad de campo (Cisneros, 2003):
Dónde: PMP es el punto de marchitez permanente, % mss; CC el contenido de humedad a la capacidad de campo, % mss.
Características del clima
Los datos de clima se tomaron de la Estación Agrometeorológica de Babiney, ubicada, a los 20° 30' 41,5" de latitud y a 76° 29’ 34,7" longitud y 58,50 msnm. El clima es tropical, el promedio de precipitaciones durante el periodo de enero abril fue de 158,93 mm. Las temperaturas medias oscilaron entre 22,7 °C en el mes de enero y 27 °C en el mes de abril. Con diferencia entre mínimas de 16,5 °C en el mes de enero y máximas de 33,1 °C en el mes de abril. Los valores e humedad relativa variaron entre el 81 % (enero) y el 77 % (abril). La velocidad del viento osciló entre 4,6 m s-1 (enero) y el 6 m s-1 (abril).
Cálculo de la evapotranspiración
Para la determinación de las necesidades hídricas se utilizaron datos climáticos de una serie de 10 años procedentes de la Estación Agrometeorológica Babiney. Para el cálculo de la evapotranspiracion del cultivo de referencia (ETo), se empleó el software ETo calculator versión 3.2, el cual utiliza los procedimientos descritos por Allen et al. (1998) y después se exportaron hacia el modelo AquaCrop versión 6.
El cálculo del intervalo entre riegos se realizó dividiendo la dosis de riego entre evapotranspiración promedio decenal, según la ecuación siguiente:
Dónde: IRes el intervalo entre riegos, d; Dr la dosis de riego, mm; ETmd la evapotranspiración media decenal, mm
Diseño experimental
Se utilizó el diseño completamente aleatorizado con tres variantes experimentales y tres repeticiones. Para lo cual se utilizaron parcelas de 4 m2 con un espaciamiento entre las mismas de 0,50 m. El cultivo estudiado fue el fríjol común, variedad INIVIT punti blanco. Este cultivar tiene hábito de crecimiento tipo I, el ciclo vegetativo varía entre 67 y 70 días y el rendimiento es de 1,21 t ha-1. La siembra se realizó con dos hileras en cada parcela.
Las variantes experimentales utilizadas se describen a continuación:
Variante 1: 0,07 m entre plantas y 0,70 m entre hileras (20 plantas por m2). 100 % de satisfacción de la demanda hídrica.
Variante 2: 0,07 m entre plantas y 0,70 m entre hileras (20 plantas por m2). 80 % de satisfacción de la demanda hídrica.
Variante 3: 0,05 m entre plantas y 0,55 m entre hileras (36 plantas por m2). 70 % de satisfacción de la demanda hídrica.
La satisfacción de la demanda hídrica por variante se presenta en la Tabla 1.
Evaluación y validación del modelo AquaCrop
Los parámetros del suelo utilizados en la investigación se muestran en la Tabla 2.
Tabla 2 Propiedades del suelo del área de investigación
| Propiedades | Valor | Unidad | Método |
|---|---|---|---|
| Densidad aparente | 1,4 | g cm-2 | (TLSFG) |
| Conductividad hidráulica | 50 | mm d-1 | (TLSFG) |
| Saturación | 52 | V (%) | (TLSFG) |
| Capacidad de campo (CC) | 43 | V (%) | (TLSFG) |
| Punto de marchitez (PMP) | 23,36 | V (%) | PMP= CC/1.84 (Cisneros,2003) |
| Agua disponible (ADT) | 196,4 | mm m-1 | ADT=10*(CC-PMP) |
| Fracción de agotamiento permisible | 0,5 | - | Criterio de Allen |
TLSFG: Tomado del laboratorio de suelos de la Dirección Provincial de Suelos y Fertilizantes de Granma
Parametrización del modelo
La parametrización es un nivel de ajuste de los parámetros específicos del modelo mayor que la calibración, aunque los dos son usados indistintamente en algunas literaturas. Por lo que respecta a AquaCrop, no hay parámetros predeterminados para el frijol común. En la tabla 3 se presentan los parámetros.
Tabla 3 Parámetros de entrada del modelo AquaCrop para la simulación
| Parámetro | V1 | V2 | V3 |
|---|---|---|---|
| CF (%) | 35,60 | 27,30 | 33,60 |
| IF (d) | 30 | 29 | 30 |
| FP | 26/01/2017 | 26/01/2017 | 26/01/2017 |
| DP (planta m-2) | 20 | 20 | 26 |
| DG | 8 | 8 | 8 |
| DF (d) | 9 | 8 | 9 |
| DM (d) | 61 | 60 | 61 |
| IS (d) | 65 | 64 | 65 |
| PER (cm) | 38,9 | 41,2 | 38,7 |
| B (t ha-1) | 2,83 | 1,98 | 3,7 |
| R (t ha-1) | 0,833 | 0,718 | 0,915 |
CF significa cobertura foliar máxima; IF inicio de la floración; FP fecha de plantación; DP densidad de plantación; DG días a la geminación; DF significa duración de la floración; DM días a la maduración; IS inicio de la senescencia; PER profundidad efectiva máxima de las raíces; B biomasa; R rendimiento
El porcentaje de cobertura foliar se estimó acorde con la metodología propuesta por Hsiao et al. (2009). Se ubicó una malla de un metro cuadrado con cuadrículas de 0,10x0,10 m sobre la cobertura foliar y se tomó una foto en plano vertical con cámara digital, marca Kodak, de 12 MP con un lente de 35 mm. Las fotos se tomaron con una frecuencia de 10 días y se procesaron con el software ImageTool para Windows, versión 3 (Wilcox et al., 2002). Para la progresión la biomasa aérea se 10 plantas cada 10 días y se secaron en estufa a 70 °C hasta peso constante.
Índices estadísticos utilizados en la evaluación del modelo
La evaluación de la exactitud del modelo se realizó a partir datos observados y simulados mediante un gráfico de dispersión. Asimismo, se utilizaron cinco índices estadísticos (3, 4, 5, 6, 7):
Dónde: R2 es el coeficiente de determinación, %; Scr la suma de cuadrados debido a la regresión; Sct la suma total de cuadrados; EF es la eficiencia del modelo; Mi los valores medidos; Si los valores simulados; M la media de los valores medidos; NRMSE el error cuadrático medio normalizado; N es el número de observaciones; EAM el error absoluto promedio.
RESULTADOS Y DISCUSIÓN
Progresión de la cobertura foliar
Al analizar la progresión de la cobertura en V1 (Figura 1A) se encontró que el modelo la subestimó en los primeros 20 días y después tuvo como tendencia la sobreestimación. El modelo no estimó correctamente la reducción de la cobertura foliar después de iniciada la senescencia al considerar un incremento de la cobertura (50 días después de la siembra). En V2 (Figura 1B) se observó que el modelo subestimó la progresión de la cobertura foliar de forma marcada hasta los 20 días, en los días posteriores se observó exactitud en la simulación de la progresión de la cobertura foliar. Respecto a V3 (Figura 1C) se aprecia que el modelo tuvo como tendencia la subestimación de la progresión de la cobertura foliar durante todo el ciclo evaluado, con igual tendencia a aumentar la exactitud en los últimos días del ciclo evaluado.
De forma general el modelo subestimó la progresión de la cobertura foliar durante los primeros 20 días y aumenta la exactitud cerca de los 40 días. La correcta simulación de CC es central para la representación de AquaCrop porque afecta la tasa transpiratoria y, en consecuencia, la acumulación de biomasa (Farahani et al., 2009).
Estas diferencias entre los valores medidos y simulados están dadas fundamentalmente por el coeficiente de crecimiento foliar, el coeficiente de reducción del follaje, los umbrales superiores e inferiores de estrés hídrico utilizados por el modelo que determinan la velocidad de crecimiento y la caída prematura de las hojas.
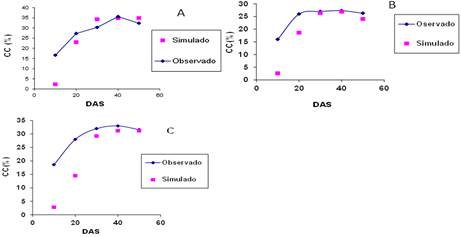 V1: (A) marco de plantación de 0,07*0,7 m y 100 % de la demanda evapotranspirativa; V2: (B) marco de plantación de 0,07*0,7 m y 80 % de la demanda evapotranspirativa; V3: (C) marco de plantación de 0,05*0,55 m y 70 % de la demanda evapotranspirativa
V1: (A) marco de plantación de 0,07*0,7 m y 100 % de la demanda evapotranspirativa; V2: (B) marco de plantación de 0,07*0,7 m y 80 % de la demanda evapotranspirativa; V3: (C) marco de plantación de 0,05*0,55 m y 70 % de la demanda evapotranspirativaFigura 1 Progresión de la cobertura foliar observada y simulada
Karunaratne et al. (2011) encontraron que el modelo subestimó la progresión de la cobertura foliar en el cultivo de maní, estudiado con diferentes variantes de riego. Heng et al. (2009) validaron AquaCrop en la simulación del cultivo del maíz cultivado en un amplio rango de condiciones ambientales, irrigadas y en secano, con estreses hídricos en diferentes etapas de crecimiento. Los autores encontraron buena concordancia de modelo simulando CC, en condiciones óptimas de riego. El modelo fue menos satisfactorio en la simulación en los tratamientos que tuvieron un estrés severo, especialmente cuando el estrés ocurrió durante la senescencia.
Farahani et al. (2009) calibraron el modelo AquaCrop para el cultivo del algodón en ambientes de riego óptimo y deficitario en el norte de Siria, los tratamientos fueron riego localizado (goteo), con cuatro niveles de riego correspondientes a 40, 60, 80, y 100 % de las necesidades hídricas del cultivo. El ajuste entre los valores de cobertura foliar observados y simulados fue bueno en todos los casos.
Progresión de la biomasa seca aérea
Al analizar V1 se notó que el modelo subestima en los primeros 20 días la producción y a partir de los 30 la sobreestima con una diferencia creciente (Figura 2 A). En V2, se encontró que el modelo tiende a sobreestimar la progresión de la biomasa aérea y de forma marcada después de los 40 días, en los días anteriores que existe exactitud en la simulación de la progresión (Figura 2 B). El comportamiento de V3 (Figura 2 C), es similar a los anteriormente discutidos. A partir del análisis anterior se deduce que el modelo no simula adecuadamente la restricción hídrica (Figura 2 C). El modelo sobreestima la biomasa sin discriminar entre el suministro hídrico óptimo o deficitario o nivel de población.
Estos resultados son similares a los obtenidos por Nazeer y Ali (2012) usando el cultivo de la cebolla como un cultivo de prueba y cuatro variantes de riego 100, 80, 60 y 40 % de las necesidades hídricas del cultivo, encontraron que el modelo mostró sobreestimación para todos los tratamientos, mientras subestimó la productividad del agua sin discriminar entre las condiciones de estrés impuestas; y con los obtenidos por Hsiao et al. (2009), quienes reportaron que el modelo no es capaz de predecir con exactitud en las condiciones de estrés hídricas severa debido a las diferentes etapas de desarrollo y características de humedad del suelo.
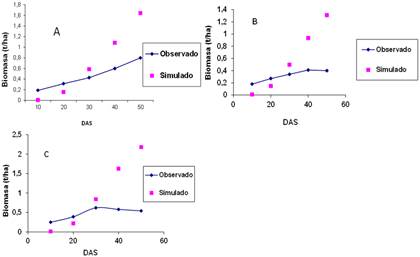 V1: (A) marco de plantación de 0,07*0,7 m y 100 % de la demanda evapotranspirativa; V2: (B) marco de plantación de 0,07*0,7 m y 80 % de la demanda evapotranspirativa; V3: (C) marco de plantación de 0,05*0,55 m y 70 % de la demanda evapotranspirativa
V1: (A) marco de plantación de 0,07*0,7 m y 100 % de la demanda evapotranspirativa; V2: (B) marco de plantación de 0,07*0,7 m y 80 % de la demanda evapotranspirativa; V3: (C) marco de plantación de 0,05*0,55 m y 70 % de la demanda evapotranspirativaFigura 2 Progresión de la biomasa seca aérea observada y simulada
Validación del modelo mediante indicadores estadísticos
De forma general se considera que simuló las fases de desarrollo bien al tener un buen valor el coeficiente de determinación R2=0,94 para V1; R2=0,94 para V2 y R2=0,92 para V3 (Tabla 4).
Tabla 4 Indicadores estadísticos de la cobertura foliar
| Descripción | CC | ||
|---|---|---|---|
| V1 | V2 | V3 | |
| R2 | 0,94 | 0,94 | 0,92 |
| NRMSE (%) | 24,7 | 28,3 | 32,8 |
| E | -0,17 | -1,61 | -2,06 |
| d | 0,87 | 0,77 | 0,73 |
Karunaratne et al. (2011) encontró valores (R2= 0,88) en la simulación de la cobertura foliar en el cultivo de maní, estudiado con diferentes variantes de riego lo que sugiere que el modelo explicó exitosamente esta variable.
Los valores de NRMSE Fueron de 24,7; 28,3 y 32 % para V1, V2 y V3, respectivamente, por lo que se considera que la simulación es aceptable según el criterio de Steduto et al. (2009). Estos valores al compáralos con los obtenidos en la parametrización del modelo AquaCrop para otros cultivos son en su totalidad superiores. Hsiao et al. (2009) reportaron valores del NRMSE entre 4,8-11 % obtenidos para algodón. Por otra parte, Farahani et al. (2009) lograron NRMSE de 9,5 %. Steduto et al. (2009) reportaron NRMSE de 8,4 % para canola. Karunaratne et al. (2011) calificaron de aceptable el NRMSE (14,75 %) estudiando el cultivo del maní con diferentes variantes de riego.
La eficiencia del modelo no se considera buena, debido a que en las variantes no se logra un valor inferior a 0,2 según el criterio de Nashy Sutcliffe (1970). Al analizar el d se puede apreciar que todos los valores están próximos a 1, lo que sugiere que d tiene un valor alto según el criterio de Steduto et al. (2009).
Los indicadores estadísticos de la progresión de la biomasa se presentan en la Tabla 5. El modelo tuvo mayor exactitud en la simulación de V1, lo anterior se confirma con los valores obtenidos de los indicadores estadísticos.
Los valores de los indicadores estadísticos para la biomasa tienen un comportamiento diferente con relación a la cobertura foliar. De forma general se puede decir que el modelo no simuló de forma aceptable la producción de biomasa y que los niveles de abastecimiento hídrico, así como las densidades son factores que introducen algún sesgo en la simulación.
Tabla 5 Indicadores estadísticos de la biomasa
| Descripción | B | ||
|---|---|---|---|
| V1 | V2 | V3 | |
| R2 | 0,99 | 0,83 | 0,52 |
| NRMSE (%) | 40 | 45 | 50 |
| E | -3,48 | -30,7 | -40,64 |
| d | 0,72 | 0,39 | 0,29 |
Karunaratne et al. (2011) estudiando el cultivo del maní con diferentes regímenes de riego encontró que el modelo explicó exitosamente la producción de biomasa con un R2(0,78). Araya et al. (2010), validó el modelo para el cultivo de la cebada con riego suplementario después de floración (0, 2, 4, 6, 8 riegos), con una densidad de población de aproximadamente 155 plantas por m2. Los resultados mostraron que para la biomasa aérea R2>0,95.
Los rendimientos observados y simulados mostraron un R2 (98,88 %), mientras que la biomasa mostró un R2 (92,5 %) (Tabla 6). El EAM para el rendimiento fue de 0,044 t ha-1; para la biomasa fue de 0,27 t ha-1. Es importante resaltar que este modelo estima el rendimiento a partir del producto del índice cosecha por la biomasa, lo que probablemente justifique el menor sesgo en la predicción del rendimiento.
Tabla 6 Valores del rendimiento y la biomasa observados y simulados
| Descripción | R (t ha-1) | B (t ha-1) | ||
|---|---|---|---|---|
| Observado | Simulado | Observado | Simulado | |
| V1 | 0,833 | 0,810 | 2,83 | 2,84 |
| V2 | 0,718 | 0,487 | 2,27 | 1,431 |
| V3 | 0,915 | 1,014 | 3,7 | 2,692 |
| R2 (%) | 98,88 | 92,5 | ||
| EAM (t ha-1) | 0,044 | 0,27 | ||
Heng et al. (2009) mostraron que AquaCrop predice el rendimiento muy bien en condiciones de riego óptimo o estrés moderado, lo cual es similar a los resultados de esta investigación. Karunaratne et al. (2011) para el cultivo del maní con diferentes regímenes de riego consideró satisfactoria la simulación del modelo al lograr un R2 de 0,72 y NRMSE de 0,36 ha-1.
La variación de la calidad y cantidad de radiación solar pueden tener efectos indirectos en la simulación de AquaCrop mediante los cálculos de ETo. La biomasa final difiere entre las diferentes variantes de riego; sin embargo, se observó que el rendimiento del grano fue bien simulado en condiciones óptimas de riego, mientras que estuvo fuertemente subestimado en condiciones de estrés.
Otros científicos (Heng et al. 2009; Araya et al., 2010) también reportaron que el rendimiento máximo simulado por AquaCrop fue subestimado en condiciones de estrés.
CONCLUSIONES
El modelo simuló aceptablemente la cobertura foliar al logarse valores del coeficiente de determinación superiores a 0,92 para las tres variantes evaluadas.
El modelo no simuló adecuadamente la biomasa, al lograrse valores aceptables solamente en la variante 1.
El rendimiento fue simulado de forma aceptable al lograrse avalar por altos valores del coeficiente de determinación y bajos del error absoluto promedio.
El modelo no simuló adecuadamente la progresión de la biomasa, y mostró diferencias de los indicadores entre las variantes analizadas














