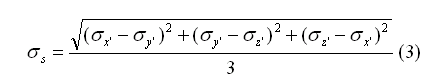My SciELO
Services on Demand
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista Cubana de Investigaciones Biomédicas
On-line version ISSN 1561-3011
Rev Cubana Invest Bioméd vol.28 no.3 Ciudad de la Habana July-Sept. 2009
TRABAJOS ORIGINALES
Modelado matemático del proceso de formación de los canales de cartílago en la epífisis
Mathematical modelling of the process of formation of the cartilage canals in the epiphyses
Liliana Mabel Peinado CortésI; Diego Alexander Garzón AlvaradoII; Rosy Paola Cárdenas SandovalIII
IMaestría en Ingeniería Biomédica.Facultad de Medicina. Universidad Nacional de Colombia.
IIDepartamento de Ingeniería Mecánica y Mecatrónica. Facultad de Ingeniería. Universidad Nacional de Colombia.
IIIMaestría en Ingeniería Biomédica. Facultad de Medicina. Universidad Nacional de Colombia.
RESUMEN
El desarrollo epifisial comienza con la formación de los canales de cartílago en la epífisis. Estos canales se forman en respuesta a los esfuerzos soportados y se extienden hacia el centro de la epífisis de los huesos. La función de los canales es transportar nutrientes y factores de crecimiento que causan la aparición del centro secundario de osificación (CSO). El objetivo de este artículo es presentar un modelo matemático que describe dos procesos biológicos. Primero, la formación de los canales de cartílago bajo la acción de esfuerzos mecánicos soportados dentro la epífisis de los huesos largos. Segundo, la presencia de factores de hipertrofia MMP9 y Runx2 en los extremos mediales de dichos canales. La solución del modelo se basa en un método híbrido utilizando el Método de los Elementos Finitos para simular los esfuerzos mecánicos presentes en la epífisis y la técnica de los Autómatas Celulares para simular la expansión de los canales dentro de la epífisis y para simular el recorrido de factores de hipertrofia dentro de los extremos mediales de dichos canales. Mediante la aplicación de este método híbrido se obtiene como resultado un patrón espacio-temporal del proceso de formación y expansión de los canales de cartílago y del proceso de transporte de factores de hipertrofia dentro de la epífisis. Estos resultados concuerdan cualitativamente con resultados experimentales previamente reportados por otros autores. Se concluye que este modelo puede ser utilizado como base metodológica para plantear un modelo matemático completo de los procesos involucrados en el desarrollo del CSO.
Palabras clave: Canales de Cartílago, Factores de Hipertrofia, Centro Secundario de Osificación, Modelo Matemático.
ABSTRACT
Epiphyseal development begins with the formation of cartilage canals within the epiphysis. The canals are extended toward the center of the epiphyses in response to the stresses supported by the bone. The canals carry nutrients and growth factors leading to the appareance of the secondary ossification center (SOC). The aim of this paper is to present a mathematical model describing two biological processes. Firstly, the formation of the cartilage canals in response to the mechanical stress present in the epiphysis of the long bones. Secondly, the presence of the hypertrophy factors such as MMP9 and Runx2 in the medial ends of cartilage canals. The solution of this model is based on a hybrid method using the finite element method to simulate the mechanical stress present in the epiphysis and the technique of cellular automata to simulate the expansion of canals within the epiphysis and to simulate the path of hypertrophy factors within the medial ends of these channels. By applying this hybrid method is obtained as a result a spatiotemporal pattern of the formation and growth process of the cartilage canals and the process of the hypertrophy factors carriage within the epiphyses. These results are in qualitative concordance with experimental results previously reported by other authors. It is concluded that this model can be used as a part of a complete mathematical model of the processes involved in the
appareance and development of the SOC.
Key words: Cartilage Canals, Hypertrophy Factors, Secondary Ossification Center, Mathematical Model.
INTRODUCCIÓN
La epífisis de un hueso largo en desarrollo (Fig. 1) se compone histológicamente de tres zonas bien diferenciadas. Primero, el cartílago articular (C.A.), el cartílago epifisial (C.E.) y finalmente, la placa de crecimiento metafisial (PC-metafisial) encargada del crecimiento longitudinal de la diáfisis de los huesos. Dentro del cartílago epifisial se forman los canales de cartílago y se desarrolla el centro secundario de osificación (CSO) mediante el proceso de osificación endocondra.1 Dicho proceso denominado osificación endocondral consiste en el reemplazo gradual del cartílago hialino por hueso.2-9 Además, el desarrollo circunferencial del CSO se presenta por una estructura cartilaginosa que lo rodea conocida como placa de crecimiento del CSO (PC-CSO).9,10 El cartílago de la PC-CSO se diferencia del cartílago de la PC-metafisial en la organización radial de condrocitos 8 que conlleva a dicho crecimiento circunferencial.10,11
Como se había mencionado, este proceso de formación de los canales de cartílago (Fig 2) es el evento inicial que antecede la aparición del centro secundario de osificación (CSO) en las epífisis de los huesos largos.6,9 Histológicamente, un canal de cartílago es un tejido conectivo laxo 12 compuesto de una capa endotelial, una membrana basal y una capa exterior.9
Los canales de cartílago se extienden dentro de la matriz del cartílago hacia la zona central de la epífisis.9,10,13-15 La expansión de estos canales ocurre en respuesta a los esfuerzos soportados por el hueso debido a la carga ejercida por los músculos adyacentes en la tracción del movimiento.16 Estas cargas producen una exudación centrífuga de solutos presentes en el cartílago epifisial mediante la ranura pericondrial.17
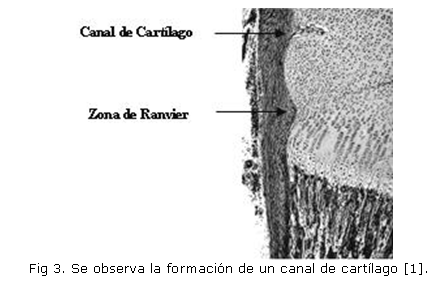
La ranura pericondrial conocida como ranura pericondrial de Ranvier (Fig. 3) es la extensión terminal del periostio,18 que forma una ranura circunferencial localizada en la periferia de la PC-metafisial y del cartílago epifisial.19Williams et al 17 sugieren que en esta ranura pericondrial, se presenta dicha exudación centrífuga de fluido hacia el pericondrio.17 Este fluido de nutrientes, factores de crecimiento, hormonas y células indiferenciadas, se realiza mediante difusión como resultado de los gradientes de presión transcortical producidos por la presión hidrostática y la carga mecánica.20
Los canales de cartílago transportan nutrientes, vasos sanguíneos, factores de crecimiento y hormonas hacia la condroepífisis.6,10,15 Durante la extensión gradual de los canales se liberan algunos factores que lideran la muerte e hipertrofia de condrocitos.21 Estos factores son principalmente las MMP9 (Metaloproteinasas de Matriz Tipo 9) y el factor de transcripción Runx2. El proceso de hipertrofia ocasiona una calcificación de la matriz circundante.9,14,15
Cuando los canales alcanzan la mitad de la epífisis, comienzan a fusionarse con otros canales para formar una cavidad central (Fig. 4).10 En esta nueva estructura se presenta mineralización de la matriz extracelular que induce la formación de la placa de crecimiento (PC-CSO).

Después de la invasión vascular y la formación de la cavidad medular, la osificación endocondral comienza con eventos biológicos similares a la osificación de la placa de crecimiento metafisial (PC-Metafisial).9 La mayoría de los estudios del desarrollo óseo se han enfocado en esta placa de crecimiento.6,10 De este modo, el conocimiento sobre los procesos mecanobiológicos involucrados en el desarrollo del CSO es limitado.10 Por tanto, para contribuir en este conocimiento, se realiza en este artículo una breve revisión bibliográfica referente al proceso de formación de canales de cartílago. Además, se propone un modelo matemático de esta formación de canales como el evento primordial en la aparición del CSO en la epífisis de los huesos largos.
Es bien sabido que los modelos matemáticos han significado un avance importante en la explicación de fenómenos relacionados con el cuerpo humano, especialmente con el crecimiento esquelético.22 Por ejemplo, Dillon y Othmer 23 desarrollaron un modelo que predice la formación de un hueso completo de un embrión de pollo. Este modelo es una buena aproximación de difusión y reacciones de sustancias en una extremidad. Sin embargo, el proceso de reacción-difusión propuesto no tiene interacción entre los componentes y el proceso de diferenciación celular no se simula por lo que se encuentra desacoplada la mitosis celular y el crecimiento de la extremidad. Un ejemplo de modelado con Autómatas Celulares es el marco de trabajo computacional creado por Izaguirre et Al 24 denominado CompuCell. Con esta herramienta se puede simular el desarrollo de organismos multicelulares y la morfogénesis de los huesos. Este modelo de Izaguirre et Al 24 es muy completo ya que incluye el proceso de diferenciación celular, de difusión y reacción de sustancias. Sin embargo, no tiene en cuenta toda la biología de formación de cada uno de los huesos e ignora el proceso geométrico implícito en el desarrollo.25 Por otra parte, Carter y Shefelbine 26 formularon un primer modelo fenomenológico usando un índice de madurez del cartílago que refleja la progresión de osificación en la epífisis de los huesos largos. Este modelo no representa la realidad de un fenómeno biológico, y sus resultados obtenidos están sin validar experimentalmente.25 Dado que no existe un modelo que describa realmente el fenómeno biológico del desarrollo epifisial, se propone realizar un primer modelo mecanobiológico de formación del CSO. Para cumplir con este objetivo, se formula un primer modelo matemático que describa la formación de canales como el primer evento que conlleva a la aparición del CSO en los huesos largos.
Por tanto, el objetivo de este artículo es presentar un modelo matemático que simule dos procesos biológicos. Primero, la relación entre la formación de los canales de cartílago con los esfuerzos mecánicos a los que se encuentran sometidos y segundo, el recorrido de factores de hipertrofia durante el proceso de formación de canales. El modelado matemático se realiza mediante un método híbrido en el cual se utiliza el Método de los Elementos finitos en la simulación de los esfuerzos mecánicos presentes y la herramienta del Autómata Celular tanto para simular la expansión de estos canales dentro de la epífisis como para simular la aparición de factores de hipertrofia en los extremos de los mismos. Con el desarrollo de este modelo se busca crear una base para trabajos futuros de modelado matemático relacionados con la descripción total del proceso del desarrollo epifisial. Para validar el modelo se realizaron simulaciones computacionales que concuerdan cualitativamente con resultados experimentales del proceso de expansión de los canales ante condiciones de esfuerzo mecánico presentes en la epífisis.
En la siguiente sección se describe el proceso biológico de la formación y extensión de los canales de cartílago e hipertrofia de condrocitos centrales y el modelo matemático propuesto. Luego se realiza la descripción de la simulación, los casos analizados y los resultados obtenidos. Finalmente se presenta la discusión de las limitaciones del modelo y las aplicaciones futuras.
MÉTODOS
Proceso biológico de formación de canales de cartílago e hipertrofia de condrocitos centrales
El primer patrón de desarrollo epifisial comienza con la formación de los canales de cartílago en el cartílago epifisial.1 La formación del canal se debe al desarrollo de una invaginación en sitios específicos del pericondrio. Sin embargo, no se conoce la razón específica que explique porque se presentan estos brotes en algunos lugares del pericondrio y en otros lugares no.10 Estas invaginaciones se extienden dentro de la matriz del cartílago de reserva no calcificada, conformada por condrocitos inmaduros, hacia el centro de la condroepífisis.6,9,10,13-15
Álvarez et al,13 proponen tres etapas espaciales del desarrollo de los canales de cartílago: superficial, intermedio y profundo (Fig. 5). En la etapa superficial, se forman canales cortos, la matriz de cartílago no está calcificada y los condrocitos no están en estado de hipertrofia. En la etapa intermedia, los canales aumentan su longitud, la matriz no está mineralizada y los condrocitos alcanzan su nivel de hipertrofia. Finalmente, en la etapa profunda la matriz se encuentra mineralizada.13
Los canales de cartílago son esenciales para el desarrollo epifisial dado que transportan nutrientes, vasos sanguíneos, factores de crecimiento y hormonas hacia la condroepífisis.6,10,15 Durante la etapa superficial, los extremos mediales de los canales transportan diversos factores de hipertrofia hacia el centro de la condroepífisis.6,10,15 En la etapa intermedia, cuando los canales llegan a la zona central de la epífisis, liberan dichos factores que lideran la muerte e hipertrofia de condrocitos (Fig. 6). Estos factores de hipertrofia principalmente son las metaloproteinasas de matriz tipo 9 -MMP9- y el factor de transcripción Runx2.9,14,15
El factor MMP9 degrada la matriz extracelular del cartílago de la condroepífisis formando un camino por donde avanzan los canales e inicia la hipertrofia de condrocitos.21 Adicionalmente, el Runx2 activa la transcripción de DNA en los condrocitos para que se diferencien a hipertróficos.27 Por lo tanto, y basado en los resultados experimentales realizados por Roach et al,9 se determina que la hipertrofia es consecuencia de la convergencia de los canales de cartílago y es la razón por la cual la zona central de la condroepífisis cambia su matriz extracelular expresando colágeno tipo X.9,28
Como se había mencionado, la expansión de los canales se debe a las contracciones de los músculos circundantes en etapa prenatal y posnatal que modulan el crecimiento y la osificación en los huesos.16 Así lo demuestran Sundaramurthy y Mao,29 en su estudio que provee evidencia experimental sobre la inhibición o activación del proceso de osificación debido a los esfuerzos mecánicos. En este experimento se aplicaban fuerzas ciclicas de 200mN con una frecuencia de 1 Hz durante 12 horas. En los resultados del experimento se observaba la aparición del CSO y la formación de un promedio de ocho canales de cartílago (Fig. 7).
Además, la extensión lateral y transversal de los canales de cartílago se presenta a través de los espacios creados alrededor de los condrocitos hipertrofiados y de los restos de condrocitos.9 De esta manera, en la zona central de la condroepífisis, los canales se fusionan con otros canales ubicados homolateralmente.14 Después de la fusión, se presenta la formación de una cavidad central que crecerá centrífugamente de manera isotrópica (Fig. 8).10 A lo largo de dicho período de extensión lateral y fusión de canales no se modifica el ancho de los mismos, sino que permanece constante a través de todo el desarrollo epifisial.14 De esta manera, las etapas de formación de canales y de hipertrofia central de condrocitos son primordiales para la aparición y formación del CSO.21

Modelo matemático
El modelo matemático del proceso de formación de los canales y del proceso de aparición de factores de hipertrofia se compone de dos partes. En primer lugar, la descripción matemática del comportamiento poroelástico del cartílago bajo esfuerzos mecánicos existentes que actúan en la epífisis de los huesos. En segundo lugar, el modelo matemático utilizado en el autómata celular para describir la formación y expansión de los canales hacia el centro de la condroepífisis y para describir la presencia de factores de hipertrofia existentes en los extremos mediales de los canales.
Modelo matemático del comportamiento del cartílago bajo esfuerzos mecánicos
El cartílago exhibe un comportamiento bifásico. Por tanto, se analiza como un material poroelástico capaz de soportar cargas.30-35 De esta manera, en el modelo matemático descrito por las ecuaciones (1) y (2), se considera que el cartílago epifisial es un material poroelástico. Además, se analiza el desplazamiento del sólido (matriz) u(t,x) y la presión p(x) del fluido desplazado por la carga experimentada dentro del cartílago epifisial.
La ecuación (1) se deriva de la ley de conservación de momento. Esta ecuación acopla la elasticidad lineal (termino 1a) con un término que representa la presión del fluido (termino 1b). En la ecuación e (u) corresponde al tensor de deformación que actúa sobre la superficie encerrada por W. ms y ls son las constantes elásticas de Lame para el sólido, relacionadas con el modulo de Young y el coeficiente de Poisson (E, n). Por su parte, la ecuación (2) hace referencia al cambio de la dilatación de la matriz sólida (termino 2a) ante la carga mecánica creada por la divergencia del gradiente de la presión del fluido contenido en el dominio W (termino 2b).36 En esta ecuación, k es una constante que representa el modulo de permeabilidad del sólido.
Para resolver estas ecuaciones (1) y (2) se utilizó el método de los elementos finitos y el método de Galerkin. Estos métodos son utilizados ampliamente para resolver ecuaciones diferenciales parciales en geometrías complejas.25
Además de modelar el comportamiento del cartílago epifisial, es necesario modelar los esfuerzos presentes en dicho cartílago. De este modo, según Sundaramurthy y Mao,29 en la epífisis de los huesos están presentes los esfuerzos cortantes octaédricos debido a la curvatura convexa de su superficie articular. Estos esfuerzos cortantes octaédricos (ss) (Fig 9) se calculan mediante la siguiente ecuación (3):
En conclusión, un modelo de simulación es fundamental para evaluar los estados tensionales en los procesos de carga sobre los huesos en crecimiento.37 Desde este enfoque Carter et al 37 y Garzón-Alvarado et al,25 suponen que las cargas mecánicas tienen un papel relevante sobre el desarrollo endocondral. Por esta razón, este artículo relaciona las cargas con la formación de los canales que conllevan a la aparición del CSO y por tanto al desarrollo epifisial.
Así mismo, en este modelo, las cargas actúan directamente sobre el cartílago epifisial. Con relación a lo anterior, Shefelbine y Carter 37 determinaron que durante el crecimiento del hueso, el cartílago es particularmente sensible a factores mecánicos por su facilidad de deformación ante cargas sostenidas en el tiempo. Y de esta forma, predicen la aparición de los centros secundarios de osificación en un modelo matemático que involucra la influencia relativa de la carga octaédrica sobre el proceso de osificación epifisial.25
Modelo matemático de la formación de canales de cartílago y de aparición de factores de hipertrofia
Para modelar la formación de los canales de cartílago en su expansión hacia el centro de la condroepífisis y la aparición de los factores de hipertrofia en los extremos mediales de estos canales se utilizó la herramienta computacional denominada Autómata Celular (A.C.).
En este estudio, el autómata celular se desarrolla sobre una cuadrícula o malla de elementos discretos diseñada sobre una geometría de una epífisis. A esta geometría se le conoce como el dominio del autómata celular. En la malla cada célula adopta distintos estados en función de su estado precedente y del estado en que se encuentran las celdas vecinas. A esta colección de todas las células y combinaciones de estados sobre la grilla o malla se denomina configuración.38 Esta configuración se actualiza en intervalos específicos cuando algunas o todas las células modifican sus estados de acuerdo a lo determinado por las reglas de transición (Fig. 10).
En resumen, el método de los A.C. tiene cuatro componentes principales. Primero, la cuadrícula en 2D. Segundo, cada célula adopta sólo uno de los posibles estados definidos. Tercero, la vecindad define el estado actual de la célula. Cuarto, existe un conjunto de reglas de transición que gobiernan los cambios en el estado de la célula.39
A continuación, se explica brevemente las reglas de transición (Fig. 11) que definen la evolución del autómata diseñado. Para comenzar, se escoge un número de celdas aleatorias de la zona del pericondrio entre el cartílago articular y la zona de Ranvier, en la cual inicia, de forma aleatoria, la formación del canal. Por tanto, cada célula escogida es el comienzo de un nuevo canal de cartílago. A cada célula aleatoria se le confiere el estado activo. La última célula con este estado activo se le considera el extremo medial del canal. Por tanto, allí se encuentra los factores que inducen hipertrofia (MMP9 y Runx2).6,10,15
Luego, en cada célula se determina el esfuerzo octaédrico promedio soportado y se extrae en una lista sus células vecinas. Así mismo, en cada célula vecina se determina el esfuerzo octaédrico promedio soportado con el fin de determinar la célula vecina con el máximo valor de esfuerzo. La célula seleccionada se le añadirá el valor activa y determinará la siguiente celda (extremo medial) de recorrido del canal de cartílago en su proceso de expansión. Esta secuencia se repite de forma sucesiva hasta que el esfuerzo octaédrico promedio de todas las células vecinas obtenga el mismo valor. En este momento se determina que los canales han llegado a la zona central de la epífisis y su expansión cesa. Estos procesos se repiten para cada célula escogida aleatoriamente. Por tanto, se obtienen dos resultados. Primero, la expansión de un grupo de canales de cartílago dentro de la epífisis. Segundo, el patrón espacio-temporal de la MMP9 y el Runx2 dentro de los extremos mediales de los canales en su recorrido hacia la zona central de la epífisis.
DESCRIPCIÓN DE LA SIMULACIÓN
La simulación de la formación de los canales de cartílago bajo la influencia de los esfuerzos mecánicos externos se llevó a cabo mediante el uso de una malla bidimensional de elementos lineales cuadriláteros de 4 nodos. La malla se extiende sobre la geometría (16 mm de ancho y 20 mm de alto) de una epífisis de un mamífero (Fig. 12).40 A partir de esta malla se obtuvieron 3990 nodos y 3864 elementos cuadriláteros que miden en promedio 0.02mm.
Como se había mencionado, la solución numérica de los esfuerzos soportados por el cartílago epifisial se realiza mediante el método de los elementos finitos usando una rutina de usuario programada en Fortran. Se realizó una simulación 2D de la respuesta del cartílago epifisial bajo esfuerzo cortante octaédrico. Además, se considera en la simulación que el cartílago epifisial es un material continuo y homogéneo.
Para las condiciones de contorno (Fig. 13) en la simulación se definen restricciones de desplazamiento nulo en el borde inferior de la geometría. Además, se aplican las cargas en el arco superior que define la zona del cartílago articular. Así mismo, se presenta la exudación de fluido por la zona de Ranvier.
La carga aplicada en la simulación se realizó considerando los parámetros que se muestran en la tabla 1.42 La simulación de la carga aplicada se realiza a partir de los datos obtenidos por Shefelbine y Carter 37 que corresponde a 1 Mpa.

Por otra parte, la simulación del autómata celular se realiza mediante una implementación computacional de las reglas de transición con dos propósitos. Primero, generar de forma aleatoria el sitio de aparición del canal y simular el camino de expansión del mismo mediado por los esfuerzos mecánicos soportados. Segundo, simular la presencia de MMP9 y Runx2 en los extremos mediales de estos canales. Para lograr estos objetivos, se utiliza como dominio la geometría de la epífisis con la misma malla bidimensional de elementos lineales cuadriláteros existente. Esta malla integrada por celdas homogéneas conforma la teselación homogénea del autómata celular implementado.
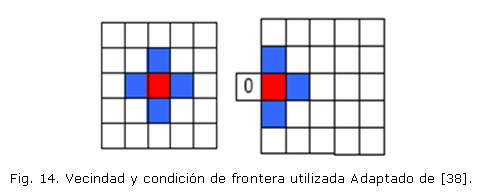
Cada uno de los elementos de cuatro nodos de la malla está definido como una célula en la implementación del autómata celular. Cada lado de la célula tiene una longitud de 0.02mm que coincide con el ancho de un canal de cartílago.43 Existen 3864 células en la cuadrícula con sus correspondientes células adyacentes que conforman la vecindad. La vecindad que se utiliza es Von Neumann que incluye cuatro células vecinas (?=4) y la condición de frontera que se implementa sobre el dominio es un límite fijo (Fig. 14). El número de estados posibles permitidos son dos: Activo o Inactivo, dependiendo si cumple con las reglas de transición. En la tabla (2) se sintetizan los parámetros requeridos para la simulación.
Para la implementación del autómata celular se utiliza una rutina programada en Fortran. Mediante esta rutina se simula en 2D la formación de los canales de cartílago dentro de la epífisis y la presencia de MMP9 y Runx2 en los extremos mediales de los canales de cartílago.

RESULTADOS
Los resultados obtenidos por medio del Método de los Elementos Finitos que ilustra los esfuerzos octaédricos soportados por el cartílago epifisial se muestra en la figura 15. Se observa que a medida que transcurre el tiempo se incrementa el esfuerzo en la zona central de la epífisis. La salida del flujo de fluido presente en el cartílago epifisial se presenta en la zona de Ranvier debido al comportamiento poroelástico del tejido. Este desplazamiento de fluido se exhibe debido a las cargas ejercidas por los músculos y tendones que ejercen un esfuerzo octaédrico sobre la epífisis.
Además, se observa (Fig. 15) que la zona de mayor esfuerzo octaédrico se concentra en el centro y se disminuye hacia las regiones laterales de la epífisis. Este esfuerzo constituye el factor mecánico que influye en el crecimiento de canales de cartílago hacia la zona central de la condroepífisis. Los resultados de la simulación de dicha formación y crecimiento de los canales se observa en la figura 16. Estos resultados se obtienen mediante el uso del Autómata Celular implementado en Fortran. Estos resultados muestran la simulación de la aparición de los canales en sitios aleatorios del pericondrio (Fig 16a). Así mismo, se ilustra la expansión de los canales hacia la región que presenta mayor esfuerzo octaédrico. Es decir, la zona central de la epífisis, lo cual es concordante con los resultados obtenidos en la simulación de esfuerzos octaédricos por el Método de Elementos Finitos.
Así mismo, se observa la fusión entre canales y la convergencia de los mismos en la zona central de la condroepífisis. Este evento ocasiona la hipertrofia de los condrocitos ubicados en esta zona por la liberación de los factores de hipertrofia que se ubican en el extremo medial de dichos canales de cartílago. De este modo, en la figura 17 se muestra el patrón espacio-temporal del recorrido de la MMP9 y el Runx2 dentro de los extremos mediales de los canales. Estos factores inducen a hipertrofia a los condrocitos centrales lo que inicia la aparición del CSO en la epífisis.
DISCUSIÓN
Este artículo presenta un modelo matemático de la formación de canales de cartílago dentro de la epífisis y la presencia de factores de hipertrofia en los extremos mediales de dichos canales. El modelo se enfoca en el comportamiento de los canales bajo condiciones de carga. De esta manera, la extensión de los canales hacia la zona central de la epífisis está modulada por el esfuerzo octaédrico soportado. Para simular la extensión de los canales se utilizó un método híbrido que consta de dos partes. En primer lugar, se modeló el esfuerzo octaédrico sobre la epífisis de un hueso mediante el Método de los Elementos Finitos. Esta simulación reveló diversas zonas de intensidad de esfuerzo debido a la geometría de la epífisis y a la dirección de la carga aplicada. En segundo lugar, los resultados obtenidos permiten implementar el método del autómata celular para simular la formación de los canales dentro de la condroepífisis y para simular el recorrido de MMP9 y Runx2 durante todo el proceso de formación de los canales.
De esta forma, los canales se extienden siguiendo un patrón que depende de los valores de esfuerzo octaédrico existente. Este hecho permite simplificar el fenómeno mediante la aplicación de algunas reglas de transición que regulan el estado sucesivo del autómata celular implementado. Bajo esta suposición, el modelo es capaz de predecir tanto la aparición de MMP9 y Runx2 en los extremos mediales de los canales de cartílago como la formación de los mismos a partir de la observación de patrones espacio-temporales en el dominio.
Por otra parte, se admite que el modelo es sólo una aproximación a la realidad del fenómeno de invaginación del pericondrio, y por lo tanto, existen dos limitaciones asociadas al enfoque utilizado. La primera limitación consiste en la simplificación hecha a la cadena de eventos moleculares que rodean la formación de un canal de cartílago. La segunda limitación se basa en que la formación de canales está modulada sólo por las condiciones mecánicas ejercidas sobre la epífisis. Aunque el modelo posee un punto de vista biológico relacionado con la presencia de factores que inducen a hipertrofia en los extremos mediales de los canales, en general, la simulación de la formación y extensión de los canales no tiene en cuenta dicho aspecto biológico. Sin embargo, esta simulación es un avance fundamental en el desarrollo de un modelo futuro de simulación mecanobiológica.
Por tanto, para lograr ampliar el modelo presentado se debe incluir los factores biológicos que ayudan a la aparición y extensión de los canales en las epífisis de los huesos largos [6][10]. Así, este modelo completo permitirá obtener resultados reales ajustados a la simulación del proceso de aparición del centro secundario de osificación (CSO). Por tanto, este modelo mecánico presentado, brinda una base para desarrollar dos trabajos futuros. Primero, un modelo mecanobiológico completo de la formación de canales de cartílago. Segundo, después de lograr el modelo antes mencionado, integrarlo dentro de un modelo mecanobiológico del desarrollo epifisial completo.
AGRADECIMIENTOS
Los autores agradecen a la División de Investigación de Bogotá (DIB) de la Universidad Nacional de Colombia que en la Convocatoria de Investigación 2009 apoyó el presente trabajo.
REFERENCIAS BIBLIOGRÁFICAS
1. Roberto Rivas & Frederic Shapiro. Structural Stages in the Development of the Long Bones and Epiphyses A Study in the New Zealand White Rabbit. Journal Of Bone & Joint Surgery 2002; 84-A(1): 85-100.
2. Liesbet Geris, Alf Gerisch, Jos Vander Sloten, Rüdiger Weiner & Hans Van Oosterwyck. Angiogenesis in Bone Fracture Healing: A Bioregulatory Model [seriada en science direct] [citado 02 02 2009] Journal of Theoretical Biology 2007; doi:10.1016/j.jtbi.2007.11.008 2007. Disponible en: http:// ww.elsevier.com/locate/yjtbi
3. Johns Hopkins. Cartilage Morphogenesis: Role of Bone and Cartilage Morphogenetic Proteins, Homeobox Genes and Extracellular Matrix. Matrix Biology 1995; 14: 599-606.
4. V. Abad, J L. Meyers, M. Weise, R. I. Gafni, K. M. Barnes, O. Nilsson, J. D. Bacher & J. Baron. The Role of the Resting Zone in Growth Plate Chondrogenesis. Endocrinology 2002; 143(5):1851-7.
5. FW Rhinelander. The Biochemistry and Physiology of Bone. 2 a. ed., in: Bourne GH (ed.). New York: editorial Bourne GH; 1972, p. 2-77.
6. Michael J.F. Blumer, Stefano Longato & Helga Fritsch. Structure, formation and role of cartilage canals in the developing bone. Ann Anat 2008; 190(4): 305-315.
7. H. C. Owen. The Cellular and Molecular Mechanisms of Glucocorticoid- Induced Growth Retardation [Tesis Doctoral]. Ucrania: The University of Glasgow Faculty of Medicine; 2007.
8. E.J. Mackie, Y.A. Ahmed, L. Tatarczuch, K.-S. Chen & M. Mirams. Endochondral ossification: How cartilage is converted into bone in the developing skeleton. Journal of Biochemistry & Cell Biology 2008; 40(1):46-62.
9. Helmtrud I. Roach, Janice E. Baker & Nicholas M. P. Clarke. Initiation of the Bony Epiphysis in Long Bones: Chronology of Interactions Between the Vascular System and the Chondrocytes. Journal Of Bone And Mineral Research 1998; 13(6): 950-961
10. Jesús Álvarez, Lorena Costales, Rosa Serra, Milagros Balbín & José López. Expression Patterns of Matrix Metalloproteinases and Vascular Endothelial Growth Factor During Epiphyseal Ossification. Journal of bone and mineral research 2005; 20(6): 1011-1021.
11. P. D. Byers & R. A. Brown. Cell columns in articular cartilage physes questioned: a review. OsteoArthritis Research Society International 2005; 14(1): 3-12.
12. S. Morini, M. A. Contineza, G. Ricciardi, E. Gaudio & L. Pannarale. Development of the Microcirculation of the Secondary Center in Rat Humeral Head. The Anatomical Record Part A 2004; 278(1): 419-427.
13. J. Álvarez, L. Costales, Alfonso López-Muñiz & J. M. López. Chondrocytes are released as viable cells during cartilage resorption associated with the formation of intrachondral canals in the rat tibial epiphysis. Cell Tissue Res 2005; 320 (3): 501-7.
14. M. A. Herrero & J.M López. Bone formation: Biological aspects and modelling problems. Journal of Theoretical Medicine 2005; 6 (1): 41-55.
15. Michael J. F. Blumer, Christoph Schwarzer, Maria Teresa Pérez, Kadriye Zeynep Konakci & Helga Fritsch. Identification and location of bone-forming cells within cartilage canals on their course into the secondary ossification centre. J. Anat 2006; 208(6): 695-707.
[16] Dennis R. Carter & Marcy Wong. Modelling cartilage mechanobiology. Phil. Trans. R. Soc. Lond 2003; 358: 1461-1471.
17. Rebecca M. Williams, Warren R. Zipfel, Michelle L. Tinsley & Cornelia E. Farnumz. Solute Transport in Growth Plate Cartilage: In Vitro and In Vivo. Biophysical Journal 2007; 93(3): 1039-1050.
18. Frederic Shapiro. Bone development and its relation to fracture repair: The role of mesenchymal osteoblasts and surface osteoblasts. European Cells and Materials 2008; 15: 53-76. Review.
19. F Shapiro, ME Holtrop & MJ Glimcher. Organization and cellular biology of the perichondrial ossification groove of ranvier: a morphological study in rabbits. J Bone Joint Surg Am 1977; 59A (6): 703-723.
20. M. V. Hillsley & J. A. Frangos. Review: Bone Tissue Engineering: The Role of Interstitial Fluid Flow. Biotechnology and Bioengineering 1994; 43(7): 573-581.
21. Joel Thomas, Kirk Melton, Nicholas M.P. Clarke & Helmtrud I. Roach. Matrix Metalloproteinase-9 Induces the Formation of Cartilage Canals in the Chondroepiphysis of the Neonatal Rabbit. J Bone Joint Surg Am 2006; 88(3): 155-161.
22. M.C.H. van der Meulen & R. Huiskes. Why mecanobiology? A survey article. J Biomech 2002; 35(4):401-14.
23. R. Dillon, C. Gadgil, & H. Othmer. Short and long range efects of sonic hedgehog in limb development. PNAS 2003; 100(18): 10152-57.
24. J.A. Izaguirre, R. Chaturvedi, C. Huang, T. Cickovski, J. Coffland, G. Thomas, G. Forgacs, M. Alber, G. Hentschel, S.A. Newman & J.A. Glazier. Compucell, a multi-model framework for simulation of morphogenesis. Bioinformatics 2004; 20(7):1129-1137.
25. D.A. Garzón Alvarado. Simulación de Procesos de Reacción-Difusión: Aplicación a la Morfogénesis del Tejido Óseo [Tesis Doctoral]. Zaragoza, España: Centro Politécnico Superior de la Universidad de Zaragoza; 2007.
26. W. F. Ganong. Review of Medical Physiology. 21nd Edition: Lange Basic science. USA: McGraw-Hill Medical: 2003.
27. Sylain Provot & Ernestina Schipani. Molecular mechanisms of endochondral bone development. Biochemical and Biophysical Research Communications 2005; 328(3): 658-665.
28. J.M. Kanczler & R.O.C. Oreffo. Osteogenesis And Angiogenesis: The Potential For Engineering Bone. European Cells and Materials 2008; 15: 100-114.
29. S. Sundaramurthy & J.J. Mao. Modulation of endochondral development of the distal femoral condyle by mechanical loading. J Orthop Res 2006; 24(2):229-241.
30. V.C. Mow, S.C. Kuei, W.M. Lai & C.G. Armstrong. Biphasic creep and stress relaxation of articular cartilage in compression: theory and experiments. Journal of Biomechanical Engineering 1980; 102(1): 73-84.
31. M.A Haide & R.C. Schugart. A numerical method for the continuous spectrum biphasic poroviscoelastic model of articular cartilage. Journal of Biomechanics 2006; 39(1): 177-183.
32. W. Wilson, C.C Van Donkelaar, B. Van Rietbergen & R. Huiskes. A Fibril-reinforced poroviscoelastic swelling model for articular cartilage. Journal of Biomechanics 2005; 38(10): 1195-1204.
33. M.A. Haider & F. Guilak. Application of a three-dimensional poroelastic BEM to modelling the biphasic mechanics of cell-matrix interactions in articular cartilage. Computer methods in applied mechanics and engineering 2007. 196(31-32): 2999-3010.
34. X.N. Meng, M.A. Leroux, T.A. Laursen & L.A. Setton. A nonlinear finite element formulation for axisymmetric torsion of biphasic materials. International Journal of Solids and Structures 2002; 39(4): 879-895.
35. J.Z Wu, W. Herzog & M. Epstein. An improved solution for the contact of two biphasic cartilage layers. J. Biomech 1997; 30(4); 371-375.
36. A.J.H Frijns. A Four-Component Mixture Theory Applied to Cartilaginous Tissues [Tesis Doctoral]. Holanda: Eindhoven University of Technology; 2000.
37. S. J. Shefelbine and D. R. Carter. Mechanobiological predictions of growth front morphology in developmental hip dysplasia. Journal of Orthopaedic Research 2004; 22(2):346-352.
38. A. Tovar. Bone remodeling as a hybrid cellular automaton optimization process [Tesis Doctoral]. Indiana, USA: University of Notre Dame; 2004.
39. D.P. Ward, A.T. Murray & S.R. Phinn. A stochastically constrained cellular model of urban growth. Computers, Environment and Urban Systems 2000; 24(6): 539-558.
40. D.A. Garzón-Alvarado, J.M. García-Aznar & M. Doblaré. Appearance and location of secondary ossification centres may be explained by a reaction-diffusion mechanism. Computers in Biology and Medicine 2009; 39(6): 554-561.
41. F.H. Setter. Section VII: Lower Limb. Atlas of Human Anatomy. Second edition. East Hanover, New Yersey: mason, S.A; 2001. p. 476.
42. D.J. Kelly & P.J. Prendergast. Mechano-Regulation of Stem Cell Differentiation and Tissue Regeneration in Osteochondral Defects," J. Biomech 2005; 38(7): 1413-1422.
43. R.A. Stockwell. Chapter 5: chondrocite nutrition, cartilage boundaries and permeability. Biology of Cartilage Cells. Cambridge: Cambridge University Press; 1979. p. 134.
Aprobado: 20 de junio de 2009
Liliana Mabel Peinado Cortés. Facultad de Medicina. Universidad Nacional de Colombia. E mail: lmpeinadoc@unal.edu.co