Nuclear Sciences
Charmonium: comparison between potential models
Charmonio: comparación entre modelos potenciales
D. A. Ramírez Zaldívar
1
*
, F. Guzmán
1
, D. Arrebato
1
1Instituto Superior de Tecnologías y Ciencias Aplicadas (INsTEC). La Habana, Cuba
Abstract
Heavy quark
cc¯
has been studied in the non relativistic framework using a quark-quark potential as a sum of power of the corresponding distance. The form of potential is based on phenomenological facts. The problem was solved numerically using a program written on C++. Mass spectra and the expectation value of the radius have been estimated for different quantum-mechanical states for
cc¯
system. The results have been compared with other similar and recent works. The mass spectra obtained is in acceptable agreement with the experimental data for
cc¯
.
Key words: charmonium; potentials; mass spectra; computer codes; schroedinger equation
Resumen
El sistema de quarks pesados
cc¯
ha sido estudiado en el marco no relativista usando un potencial quark-quark de la forma de la suma de potencias de la distancia entre las partículas. El problema se resolvió numéricamente usando un programa escrito en C++. Se estimaron el espectro de masa y el valor esperado del radio para diferentes estados de excitación. Los resultados fueron comparados con otros trabajos similares recientes. El espectro de masa obtenido concuerda de manera aceptable con los datos experimentales para el sistema
cc¯
.
Palabras-clave: charmonio; potenciales; espectros de masas; códigos para ordenadores; ecuación de Schroedinger
INTRODUCTION
The most reasonable formalism to treat the hadronic dynamic after a collision is Quantum Chromodynamics (QCD). At high energies, the most basic calculus admit a perturbative approach but it is well known that the QCD is not appropriate to treat problems at low energies because the cross section is linked with the coupling constant
as
and at low transferred momentum the coupling constant takes values that make impossible a perturbative treatment. Then to explore hadronic states were
Q2
is low, we do not follow the conventional treatment of QCD and it is necessary to find another way to do this. The Schrodinger formalism has proved to be an adequate way to attack non-relativistic problems at low energies were the invariant mass much larger than the transferred momentum, and there is much work that has used this framework to confront the problem of hadronic states, principally applied to heavy mesons [1-3]. For this task, one of the most frequently used procedures is the potential model method, with some fitting parameters.
We want to explore
cc¯
system employing the Schrodinger formulation using a new approach of potential inspired on experimental facts. There are two principles of QCD that are extracted from the experiment: asymptotic freedom and color confinement. Following the asymptotic freedom and make a classical interpretation our potential must have a local minimum to minimize or annulated the interaction force. We know that the effective nuclear force has a short range and to reproduce this phenomenon we include a negative exponential term.
We estimated mass spectra, the expectation value for quark-quark distance and compared with the results obtained for other authors that had used similar formalism. Our calculations were compared with the Cornell model and with an energy-dependent potential.
Theoretical framework
To calculate the mass spectra of the system, we use the stationary Schrödinger wave equation:
HΨ=EΨ\
(1)
The system is composed of a quark and antiquark of the same flavor: charm. The easiest way to solve this two-body problem is by using the center mass system and reduces it to one particle with a reduced mass
μ
. Due to the spherical symmetry of the problem we separate the radial part of the angular part and after some algebraic transformation the radial equation to solve it becomes:
y′=2μ(Veff−ε)y\
(2)
Veff(r)=ar+βre−ηr+l(l+1)2μr2
(3)
All expressions are written in natural units. As we mention before, we use a phenomenological potential with three parameters. To certain combinations of such parameter (
α,β,η
) we have a potential that has a local minimum as we want because the objective is to create a region were the interaction force vanished or at least reached a minimum. This point will be a classical equilibrium point.
DVR METHOD
To solve the problem numerically, we used Discrete Variable Representation (DVR) method [5,6]. The DVR is a grid-point representation, and it solves the problem of integral evaluation because there are no integrals to evaluate. All that we need is to calculate the eigenvalues and eigenvectors of a matrix H. The eigenvalues give us the mass spectra and the eigenvector give us some coefficient (
Cni
) necessary to express the eigenfunction or Hamilton operator. We discretize the space to one-dimensional problem and for a particle with mass m in a potential V(r), then we have:
ri=a+(b−a)Ni,i=1,2,...N−1
(4)
The H matrix elements
Hij
are given by:
Hij=Tij+Vij
(5)
Vij=δijV(ri)
(6)
were
Tij
are given by:
Tij=Δr2m∑n=1N−1φn(ri)φn′´(rj)
(7)
We can obtain the following expression to the kinetic matrix for selected generic basis.
Tij={π2(−1)i−j4m(b−a)2(1sin2((i−j)πN)−1sin2((i+j)πN))i≠j(π4m(b−a))2(2N2+13−1sin2(iπN))i=j
(8)
The energies of the excited levels are the H matrix´s eigenvalues. The wave function is obtained by:
ψn(r)=∑i=1N−1Cniφn(r)
(8)
φn(r)=(2b−a)12sin(nπ(x−a)b−a),n=1,2,...N−1
(9)
Coefficient
Cni
is an i-esim component of the eigenvector n-esim. As we have real wave functions, then the expectation value of
f(r)
is the solution of:
〈f(r)〉n=∫abf(r′)ψn2(r′)dr′
(10)
RESULTS
Using a program wrote on C++ we computed those expressions to solve the problem of eigenvectors and eigenvalues and choose the basic level to fit the potential parameters. In Table 1.,the results obtained for mass spectra to l=0, compared with Cornel potential and Lombard potential are presented.
Table 1 Mass spectra (GeV) comparison between Experiment [1], Cornell [1], Lombard [2] and calculated.
| |
Experiment |
Cornell |
Lombard |
Present work |
| 1S |
3.096916(11) |
input |
Input |
input |
| 2S |
3.68609(4) |
input |
3.685 |
3.786 |
| 3S |
4.039(1) |
4.120 |
4.037 |
4.046 |
| 4S |
4.415(4) |
4.490 |
4.249 |
4.381 |
|
a(GeV2)
|
0.480 |
|
β
|
3.514 |
|
η
|
0.209 |
|
mc(GeV)
|
1.37 |
The error of the method is given by the size of the basis set that expresses the number of intervals. Then we can make this error as small as we need it. Results obtained for <r>, <1/r> and
〈r2〉
are listed in Table 2, compared with Gupta-Mehrotra [3] calculation.
Table 2 <r>, <1/r> and
〈r2〉
.
| |
<r> (GeV
-1
)
|
<1/r>(GeV) |
〈r2〉
(fm)
|
| |
Present work |
[ref] |
Present work |
[ref] |
Present work |
[ref] |
| 1S |
1.002 |
2.790 |
2.516 |
0.507 |
0.366 |
0.456 |
| 2S |
1.551 |
4.612 |
1.194 |
0.396 |
0.670 |
0.898 |
| 3S |
1.900 |
5.9 |
0.683 |
0.343 |
0.855 |
1.252 |
DISCUSSION
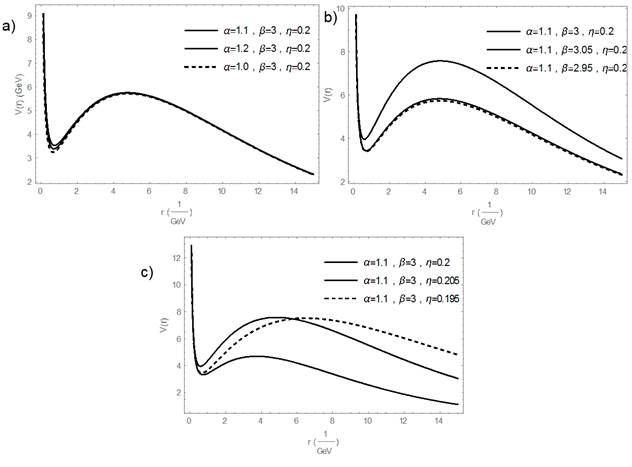
The potential and then the calculation is very sensitive to the variation of 𝛽, and 𝜂 parameters respect to the variation of
α
parameter. In figure 1 are shown three plot of potential to different values of fit parameter were the variation of
α
is the 200% of 𝛽 and 𝜂. To
α
variation, the shape are practically the same but change drastically with the change of the other parameters.
The method used converge rapidly. For N=35 the relative error is less than 1%, but we chose N=50 to achieve a relative error inferior to relative experimental error.
The are many combinations of potential parameters to fit the experimental mass spectrum, but we choose the set of values that maintain a local minimum, to keep the initial phenomenological interpretation. Although our potential is very different from other approaches, we obtained good agreement with the experimental mass spectra. The maximum error is of 2% that is reasonable good.
The results obtained for <r>, <1/r> and
〈r2〉
maintain similar behavior and the same magnitude order of the reference, but we cannot say that it is a lousy estimation as we must keep in mind that reference values are estimated using a potential model too. However, we can mention that the order of magnitude has a good correspondence. We cannot fix a lower limit, but we can predict an upper limit which can be approximated by the distance at the potential taking a value greater than the invariant mass. At these intervals, we know from QCD that the cross section favors the creation of another pair of quark and antiquark and reconnects to create a two-
cc¯
system that is greater than the probability that the system remains coupled.
CONCLUSIONS
Heavy quarkonia system
cc¯
has been studied in the framework of non-relativistic Schrodinger equation with an approach of quark-antiquark potential. The method used show a fast convergence that makes it an excellent choice for a rapid fitting of potential parameters. The mass spectra calculated was in good agreement with the experiment. The estimation for <r>, <1/r> and
〈r2〉
has acceptable values in comparison to the references estimation with another potential. The presented approach of quark-quark potential can be a new starting point for energy-dependent potentials and new research using this formalism.
References
1.
[1] Quarkonium: Final Paper in Strong Interactions. NirGuttman - 043119338. Tel Aviv University, 2010. [ Links ]
2.
[2] LOMBARD RJ, MARS J & VOLPE C. Wave Equations of energy dependent potentials for confined systems. J Phys G: Nucl and Part Phys. 2007; 34(9): 1879-1888. [ Links ]
3.
[3] GUPTA P, MEHROTRA I. Study of heavy quarkonium with energy dependent Potential. J Mod Phys. 2012; 3(10): 1530-1536. [ Links ]
4.
[4] EICHTEN E, LANE KD, et. al. Spectrum of Charmed Quark Antiquark Bound States. Phys Rev Lett. 1975; 34(6): 369-372. [ Links ]
5.
[5] LIGHT J C, HAMILTON IP & LILL JV. Generalized discrete variable approximation in Quantum mechanics. J Chem Phys. 1985; 82: 1400. [ Links ]
6.
[6] COLBERT DT, MILLER WH. A novel discrete variable representation for quantum mechanical reactive scattering via the S-matrix Kohn method. J Chem Phys. 1992; 96: 1982. [ Links ]