INTRODUCTION
In the study of elastic scattering of atomic nuclei at low energies there has been a long-lastinginterest in the so-called threshold anomaly (TA [1]). This is an effect that becomes evident when experimental elastic scattering angular distributions, measured at several energies aroundthe Coulomb barrier VCare adjusted by means of the Optical Model (OM). For the case of tightly bound nuclei, thisphenomenon,is related to the closure of reaction channelsat bombarding energies below the Coulomb barrier. It is manifested as a decrease of the depth of the imaginary part of the optical potential at energies below VC. Due to the dispersion relation (DR [1]) linking the real and imaginary partsof the optical potentials, the depth of the real part also varies strongly, peaking around VC (seeRefs. [1,2,3]), thusimplying, a more attractive potential. Conversely in the case of weakly bound projectiles, the coupling to non-elastic channels (e.g. the breakup channel) generates a repulsive polarization potential [4] that can produce, either the absence of TA (no TA [5,6,7,8]) or the so-called breakup threshold anomaly (BTA [7,8,9]), in which the imaginary potential increases while the real potential decreases in the proximity of VC.[9,10]. In the present work new results onexperimental elastic angular distributions in the 9Be+80Sesystem are presented. The data were analyzed using the OM with three different types of potentials, namely, a semi-phenomenological double folding potential with two free parameters known as the Sao Paulo Potential, a Wood-Saxontype potential with six free parameters, and an exponential potential with two free parameters. The result of this analysis is presented in section III.-Results. It will be shown in section IV.-Discussion that the three potentials yield the same results: the 9Be+80Sesystem clearly presents aBTA , independently of the potential used to reproduce the angular distributions.
MATERIALS AND METHODS
The elastic scattering angular distributionswere measured at eleven bombarding energies: 17, 18, 19, 20, 21, 22, 23, 24, 30 and 32.8 MeV (VC ≈ 20 MeV). Beams of 9Be ionswere delivered by the 20 MV tandem accelerator of the TANDARLaboratory in Buenos Aires. Enriched (99.8%) 80Se targets, 110 µg/cm2 thick, evaporated onto 20 µg/cm2 thick carbon foils, were used. The detection system consisted of an array of eight surface-barrier silicon detectors with an angular separation of 5 degrees between adjacent detectors. The angular distributions were taken inangular steps from 1 to 5 degrees, depending on the energy andangular range. A second set of two surface-barrier detectorswith an angular separation of 8 degrees were placed ina second rotating support at the top of the scattering chamber,to measure the reaction products at the most backward angles.The energy resolution of the detectors (FWHM) ranged from 0.5 to 0.8%, which were enough toidentify and separate inelastic-excitation peaks from theelastic one. For normalization purposes two additional surface barrier detectorswere placed at ±16 degrees. Theangular opening of these so-called monitor detectors, defined bycircular 1.5 mm-diameter collimators, was about 0.25 degrees. Further details of the experiment are given elsewhere [11].
RESULTS
Typical angular distributionsfor two energies (E lab = 18 and 30 MeV) are shown in Figure 1.Model calculations were performed with a) a Sao Paulo potential with free N r and N i (normalization factors for the real and imaginary parts, respectively), b) a Wood-Saxon potential with real part characterized with parameters V, r 0, and a, the depth, the radius parameter and the diffusivity respectively, an imaginary part, divided in two components, a volume part with fixed parameters V i = 10 MeV, r i0 = 1.0 fm and a i = 0.15 fm and a variable surface part with parameters V si,r si0 and a si and c) anoptical potentialwhose real and imaginary parts areV = V 10*exp((10-R)/a) and W = W 10*exp((10-R)/a)respectively, with a common rateparameter a = 0.65 fm. The two free parameters, V 10and W 10, represent the magnitude of the corresponding exponential functions, at an arbitrarily chosen radius, in our case 10fm. A feature of this method is its simplicity; in this way,complex algorithms or sets of numerous and ambiguous geometric parameters are avoided.
The three potentials at E lab = 30 MeV are compared in Figure 2. Although the three potentials are very different in the nuclear interior region they are quitesimilar at the nuclear surface where it is expected that most of the absorption will take place.
As indicated in the Figure 2 the results for the three potentials are shown for two energies. Very reasonable fits are obtained at all energies.
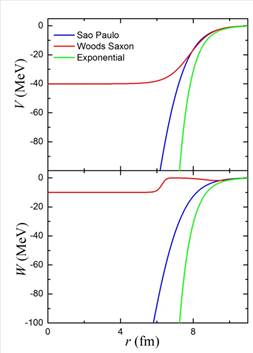
Figure 1 Real and imaginary parts of the three optical potentials discussed in the text. (For the Woods Saxon potential W represents the sum of the volume and surface components).
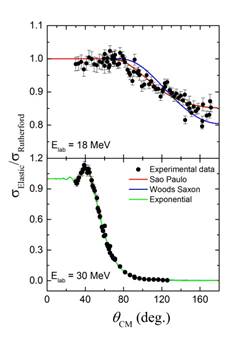
Figure 2 Elastic scattering of 9Be+80Se at bombarding energies of 18 and 30 MeV. Solid lines represent the optical model calculations as indicated in the figure (for E lab = 18 MeV the curves of the Sao Paulo and the Exponential overlap, and forE lab = 30 MeV the results are indistinguishable in the scale of the figure).
The values of the parameters for the different potentials as a function of the bombarding energy,are presented in Figure 3.The uncertainties of the parameters are obtained by means of the covariance matrix method as described in Refs. 12 and 13.
DISCUSSION
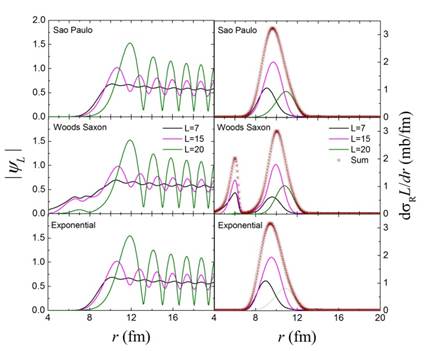
As it was pointed out previously, three types of algorithms have been used in order to generate optical-model potentials. These potentials, as shown in Figure 1, are very different at low radial distances but quite similar over the peripheral ones, where most of the absorption takes place. Despite these circumstances, different physical quantities given by the optical model calculations are nearly coincident. First of all, the best fitted elastic differential cross-sections; some examples shown in Figure 2. They are obtainedwith equivalent parameters, which, of course, are different in absolute value but follow coherent behaviors as a function of the bombarding energy, as may be observed in Figure 3. As it is shown in Figure 4for E lab = 30 MeV, the partial reaction cross-sections are quite similar. The same may be remarked in Figure 5 for three examples of the module of the partial wave-functions; in these cases, those corresponding to the maximum orbital angular-momentum that contributes to the reaction cross-section, and those which correspond to about the half of that maximal contribution. In the case of the spatial distributions of the absorption cross-section displayed in Figure 5, the coincidences are clear for the Sao Paulo and the exponential approximations; the Woods-Saxon potential, that includes an important internal imaginary potential, leads to a shift of the internal parts of the peripheral peaks given by the two other approximations to the inner of the target, keeping their magnitude. The study of the behavior of this spatial distribution over the peripheral region at energies close to the Coulomb barrier may be useful to determine the presence of the normal or the breakup threshold anomaly.
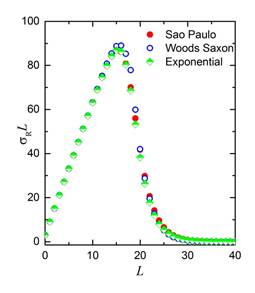
Figure 4 Partial reaction cross-sections as a function of the orbital angular momentumLfor E lab = 30 MeV. The values corresponding to each kind of potential (see text) are represented by a different symbol.
We calculate the absorption density at each radius as the sum over angular momentaL of the product of the imaginary potentialW times the absolutesquare of the wave function
Figure 5 shows the absolute value of the partial wave functions and the partial absorption density as function of radius for the different potentials.
CONCLUSIONS
The behavior of optical-model parameters used to describe elastic-scattering angular distributions for the9Be +80Se system, which in this work are analyzed as a case study, clearly showsa breakup threshold anomaly at bombarding energies below the Coulomb barrier. This can be attributed to the low binding energy of the 9Be projectile which favors its breakup in approaching the 80Se target. It has been also shown that this conclusion is independent of the choice for the nuclear potential model. Moreover, an extremely simple model as the exponential potential,has proven to be successful in reproducing the experimental data.