Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de Protección Vegetal
versión On-line ISSN 2224-4697
Rev. Protección Veg. v.22 n.1 La Habana ene.-abr. 2007
Trabajo original
MATHEMATICAL MODELS IN CROP PROTECTION
MODELOS MATEMÁTICOS EN PROTECCIÓN DE PLANTA
Richard Levins* and Ileana Miranda**
*Harvard School of Public Health. Boston, MA 02115 USA. Académico del Instituto de Ecología y Sistemática, Cuba. E-mail: humaneco@hsph.harvard.edu; **Centro Nacional de Sanidad Agropecuaria (CENSA), Apartado 10, San José de las Lajas, La Habana, Cuba
ABSTRACT
In the present work, the models of dynamics ecological populations were described. The development of the models, in order to describe these populations was presented. They have evolved from an independent way to the models that represent the evaluation of epidemiology in humans. The differential equations that describe the relationships prey-predator, crop-pest and migration effect were shown. It was also described the possibility to represent these models by means of equations in difference and computerized simulation systems. The interconnection between a mathematical model and the ecosystem stability according to the biological parameters was showed. Ecological questions that can be answered analyzing the models were approached.
Keys word: Mathematical models; prey; predator; migration; ecosystem.
RESUMEN
En el presente trabajo se describe la evolución que ha tenido la modelación del crecimiento de las poblaciones. Se presenta el desarrollo de los modelos que describen estas poblaciones, los cuales han evolucionado de manera independiente a los modelos que representan la evaluación de la epidemiología en humano. Se muestran las ecuaciones diferenciales que describen las interacciones presa-depredador, cultivo-plaga y el efecto de migración. Se describe, además, la posibilidad de representar estos modelos mediante ecuaciones en diferencia y sistemas computarizados de simulación. Se muestra la interconexión entre un modelo matemático y la estabilidad del ecosistema según los parámetros biológicos. Se abordan preguntas ecológicas que pueden ser respondidas analizando los modelos.
Palabras clave: Modelos Matemáticos; presa; depredador; migración; ecosistemas.
INTRODUCTION
Mathematical studies of epidemics in human populations and models of the spread of agricultural pests and diseases developed independently (28, 24). MacDonald's modeling of malaria (21,23) and Vander Planck's plant epidemiology, belong to two very different intellectual communities, were located in different institutions, and published in journals that had few readers in common (10,25,32). And yet their basic intellectual problems were the same: the understanding, predicting, and intervening in the population dynamics of species that share our ecological space and may harm us (26). Both fields are grounded in population ecology (13) and share the methodologies of differential equations, difference equations (9), and computer simulation to represent predation, contagion and parasitism (22,31). More recently, with the emergence of new diseases and the resurgence of old ones, has it become obvious that these fields of research and also veterinary epidemiology overlap and can benefit from each other (8).
The goal of economic entomology and plant pathology is not the elimination of a pest or disease but the Protection of the harvest in a way that it is inexpensive, protects agricultural workers and consumers, and does not harm environment or make our production system more vulnerable to future outbreaks. Sometimes this does require eliminating a pest, but not always (11). The pest may be diverted to other, less valuable, trap crops. A virus might infect a plant only after the critical period when it can inhibit plant growth and development so that we aim to delay its arrival. An herbivore may feed on parts of the plant that do not affect yield (the rice yield depends on the uppermost leaf only). A bird might eat some grain but also feed on the herbivores. The woodpecker might drill into cacao pods, but only the damaged ones, to feed on the herbivores that are already there. The sorghum shoot fly kills the growing stem of a sorghum plant. This stimulates till ring, the growth of new shoots from secondary buds, and might actually increase yield. It is harmful only because the shoots are not of uniform height and make harvesting more difficult in mechanized systems. An herbivore that feeds on the lower, shaded tomato leaves may reduce humidity that favors fungi, and remove al location of respiration that does not photosynthesize (16). When tomatoes ripen, exposure to sunlight is beneficial and herbivores that remove the upper leaves improve fruit quality. Therefore the starting point of our work has to be to determine what various species in the agro-ecosystem really do to the harvest (9).
Ordinary differential equations are continuous models (9). Therefore they presume that all stages of the life cycle of a population are present and generations overlap. They have the advantage of being more familiar than other methods. If populations have many generations in the year, such as aphids or mites, a continuous model is a reasonable approximation (6). They do not take into account the changing parameters during the day, or day to day weather variation, since these observations are usually not available, but often can be averaged (15). Nor do they usually recognize different life stages in the insects although we could write separate equations for each stage (3,34).
In what follows, we emphasize models aimed at understanding the sometimes surprising behavior of the non-linear complex dynamics of elements of the agro-ecosystem (2). For that purpose we will use ordinary differential equation, and ess familiar techniques of signed directed graphs, time averaging, and cellular automata.
DESCRIPTION OF THE BIOLOGICAL SYSTEMS USING DIFFERENTIAL EQUATIONS
In order to describe the biological system, we used equations having the form
where x, y, z… are species or other population variables.
Systems of differential equations can be solved numerically by computer to show the trajectory of the variables provided if we know the parameters (33). Or if we do not know the parameters, we can use part of the data to estimate them statistically and then test the model on the rest of the data (14, 29).
Difference equations are more suitable when a population has distinct cohorts starting with an invasion of a field or emergence after spring rains or the first flush of young leaves, and has few generations in the year. Changes within the time period of the model are absorbed within its parameters and we have:
- Simulating differential equations
When we use computers to simulate differential equations, the iterations make them really difference equations with short intervals (35). These difference equations are descriptive using the dependence between n+1 success and n success
, with perhaps also delays, so that
When we work with differential equations, oscillations are usually represented by the period and amplitude, often found from Fourier analysis (5). In difference equations the semi-cycle length is more common. The semi-cycle is the number of consecutive steps on one side (below or above) equilibrium (7). It is more easily determined from data since we can never really demonstrate that a variable has returned exactly to a previous value but we can easily detect peaks and troughs of the trajectory. When the motion is chaotic, it can show sequences that seem to be periodic of all periods but the semi-cycles can still be limited and can characterize the dynamics.
- Method of time averaging in order to determine the observed variation in a system
Time averaging is based on a single very powerful theorem: if x is a bounded variable, then the average of its derivative in the long run is zero (7). The average or expected value of the variable is:
It has a variance 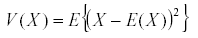 and similarly we define the covariance by
and similarly we define the covariance by 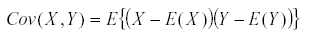
These formulas are used for determining what drives the observed variation in a system. For instance, suppose that we have an herbivore H and a predator P related by the equations system:
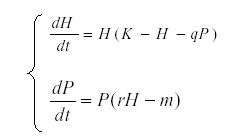
This model is useful in order to simulate prey – predator interaction (6, 14, 27, 35), K is the carrying capacity for H and q the predation rate, r the reproductive rate of the predator and m its mortality. But, if we suppose that K is dependent on environmental conditions and therefore varies while the other parameters are constant, then we start with the autonomous equation and find the expected value:

The expected value of the left hand side is 0, E{rH-m} =0 and the average herbivore level is m/r, independent of K.
Using define the covariance, we find that Covariance (H, P) =0. We can now use this result in equation of H in the equation system (P, H). Dividing by H, we find that E{K-H-qP} = 0 and that Covariance (H,K) = qVar(H).
Therefore when the system is driven from below, H tracks K and the predator is uncorrelated with its prey (it lags 90o behind H). But if the system is driven from the predator end, say with variable mortality m, then we begin with the herbivore equation:
- Variance (H) –q Covariance (H,P) = 0 so that Covariance (H,P) = -Variance (H)/q, showing that the covariance of predator and herbivore is negative. Thus the mathematical model tells us how to identify the source of environmental forcing in the system.
If we change the model so that the predator is density-dependent its equation may become 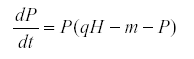
Then when K is the environmental variable we find that qCov(H,P) = Var(P) >0.
Awerbuch et al. (1) and González et al. (12) showed that in the scale insect-wasp-fungus system in citrus, the scale Lepidosaphes gloverii is positively correlated over time with its enemies. This supports the interpretation that the annual cycle is driven from below, from seasonal changes in the trees or climate affecting the scale directly and its enemies indirectly. But when we look across trees and sections of trees at any one time, the correlation is negative. That implies that the differences among trees act directly on the enemies and from them to the scales.
The method of time averaging can be applied to more complex communities. These can best be understood with the help of signed directed graphs (loop analysis).
- Signed directed graphs. Evaluated at equilibrium
The method of signed digraphs represents n ecological community by a network, a graph in which the vertices are the variables (usually the numbers of a species or a stage in that species) and the sides connecting them are the interactions. Suppose that we have a system of equations.
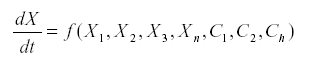
Where Xi represents the variables and Ci are the parameters.
The Jacobean matrix is the matrix of the first partial derivatives with the element ai,j =-------fi/xj.
This is evaluated at equilibrium, when all the fi = 0. The term aij is the direct effect of variable j on variable i. It is represented in the graph as the line from xj to xi. Since we often only know the sign of that effect, the direction of impact, we represent a positive aij by a sharp arrow - ® and a negative effect by a round arrow head, —o. We usually know the sign of an interaction even if we do not have an equation for it. Thus predators reduce their prey and the prey increases the predator. There are two ambiguous cases. If variable xj affects variable i in different ways by different pathways then we have to introduce the intervening variables. For instance if cyanobacteria inhibit green algae by secreting a toxin but also fix nitrogen that the green algae can use, we could introduce nitrogen as an additional variable, increased by the cyanobacteria and increasing the green algae, and then have a direct negative link from the cyanobacteria to the green algae to represent the toxic effect. We could also have done it differently, representing the toxin as an intermediate variable and nitrogen fixation as a direct positive effect (23).
The second kind of ambiguity is whether to include a link from a variable to itself, referred to as auto-inhibition or self-damping. That can be answered by looking at the aii. A general guideline comes from the form of the equations. Suppose that:

Where X1 does not enter into f1 this is simple reproduction. The derivative with respect to X1 is:
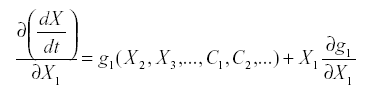
At equilibrium, either x1=0 or g1(x2, x3,…c1, c2,…) =0. If species i is part of the system it is not zero, so g1 =0, and since x1 does not appear in g1 the partial derivative is also zero. Therefore simple reproduction implies zero self-damping (aii =0).
A variable which is not self-damped behaves as a sink in the system. On the other hand, if xi is produced by something else, as in chemical transformations or the photosynthate then let  .
.
Then the first partial with respect to x1 is –g(x2,x3,…) which equals -A at equilibrium. Therefore variables which are not self-reproducing are usually self-damped.
At the bottom of every ecosystem there are some self-damped variables such as available nutrients. If we chose not to include these nutrients in the model, their self-damping is transferred to the next link up the trophic scale. For instance suppose that some mineral is formed from geological processes in the subsoil and reaches the plants at the rate a suppose further that the plant’s growth is determined by this nutrient. Then we may have

Where M is the nutrient concentration, a is the rate of release of nutrient from the substrate, H is the plant biomass, c the removal of nutrient by other processes, and d the rate of removal of plant biomass by senescence or herbivore. Other parameters are omitted for simplicity of exposition (36). From the equation system, M reaches an equilibrium at  , substituting that value in equation for
, substituting that value in equation for  gives
gives 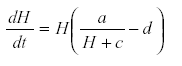
Now differentiate with respect to H:
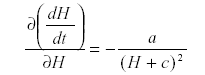
which is -a/d2 so that H is self-damped. Self damping is an important property of systems.
There is a correspondence between the matrix of first partials and the signed digraph. Define a cycle in the graph as a sequence of links from variable xi back to xi with each variable on the cycle having only one input and one output. The value of the cycle is the product of the aij around the cycle. A path Pij a sequence of links from variable j to variable i that does not cross itself. Each variable on the path except the first and last has one input and one output. The path Pii is assigned the value Pii =1.
The determinant of the matrix is a sum of products of the aij around cycles that do not overlap. Suppose the L(m,n) is the product around m disjunctive cycles with a total of n terms in a matrix of order n. Then we define the gain (or feedback) of that determinant as:
Fn = åÕ(-1)m+1L(m,n)
Over all m£n. That is, it is the sum of the products of all disjunctive loops totaling n terms. The (-1)m+1 assures that if all terms L in a product are negative then that term contributes negative feedback to Fn and if all cycles in a network are negative then its feedback is negative. By convention, F0= -1. Finally, the complement of a path is the remaining graph after the path is removed.
The graph can be used to study the local stability of the system and also the effect of parameter change on the equilibrium levels of the variables. It is most useful when the matrix is sparse, that is when most aij =0.
The standard procedure for using the signed digraphs is to develop a table of the signs of change of equilibrium levels of the variables when a parameter is changed. Figures 1-5 show several examples of ecosystem structures and their consequences and were selected as examples in order to illustrate how we can use these models to answer qualitative questions about agro-ecosystems.
QUALITATIVE QUESTIONS
One of the most frequents question is: Why does an abundant natural enemy sometimes fail to reduce a pest? (10).This always suggests that there is a sink absorbing the impact of parameter change. For instance in Figure 1 let a plant biomass B is utilized by an herbivore H which is preyed on by a predator P. An input (change of parameter) that enters the system by way of the plant (the amount of mineral nutrients, water or sunlight that favor plant growth) affects plant biomass to the extent of the impact itself times the path to the plant equal 1 times the feedback of the complement (the herbivore-predator feedback loop) divided by the feedback of the whole system (in this case –(self damping of plant) (herbivore/predator loop). The direct impact is positive, the path is positive, the complement has negative feedback and the denominator is also negative. Thus the impact of parameter change favoring the plant increases the plant biomass. The same parameter change spreads to the herbivore providing more plant matter to feed on. Therefore this is a positive link. Its complement is the subsystem of the predator alone, here taken to have no self-damping. Therefore, the population level of the herbivore will not change. But the path from the plant to the predator is positive. The complement has 0 elements and therefore its feedback is -1, and the denominator is negative. Thus the effect of improving conditions for the plant in this model increases the plant and the predator but leaves the population of the herbivore unchanged. This is understandable when we realize that the reproduction of the herbivore is increased by more food but is consumed faster by the increased predator. Herbivore numbers are unchanged, but the individuals are younger since mortality is greater.
Similarly, a positive input to the herbivore such as a more favorable temperature gives a negative path to the plant, but the complement is the zero feedback of the predator and so the plant population is unchanged. The impact on the herbivore population is also 0 since the complement is the feedback of the predator. Finally, the positive input to the herbivore has a positive pathway to the predator so that the only change is an increase of the predator. Changes which impinge on the predator reach the plant by a positive path (negative times negative), the complement of this path has zero elements and therefore is -1 and the denominator is negative. Therefore a change favoring the predator increases the plant. It has a negative link to the herbivore with a negative complement and denominator resulting in a decrease in herbivore. And finally, the input to the predator is positive and the complement is the subsystem herbivore-plant which has negative feedback. In this model, yield can be improved by fertilizing the plant or increasing the predator but not by killing the herbivore. In fact, the use of pesticides can increase the herbivore: the direct negative impact on the herbivore is nullified by the zero complement of the predator while the negative impact on the predator is multiplied by a negative link to the herbivore to give a positive effect. The use of chemical pesticides often increases the herbivore pest, not because it is more sensitive physiologically to the chemical but because of its position in the network. It is harmed by the pesticide but that effect is absorbed by the predator, and it is facilitated by the poisoning of its natural enemy. The predator suffers loss both from the direct toxicity of the pesticide and by the killing of its prey.
Note that the conclusion does not depend on any exact equations for any of the variables. The structure of the network, the signs of the links among them are suffice for qualitative conclusions. If we encounter a situation where an intervention against a pest increases its numbers, we should look for a natural enemy that we are poisoning.
The table of effects on the equilibrium levels and also, by a different argument on the average levels can be used to interpret the observed correlations among the variables. If there are improvements in the crop conditions, changes in the yield should not be correlated with the pest population but would be positively correlated with the predator. If change enters the system at the herbivore level, there will be negative correlation between the crop and the predator but neither will be correlated with the herbivore. Changes acting on the predator will result in a positive correlation between predator and yield, and both will be negatively correlated with the pest population.
How do we identify the most important natural enemy?
Suppose now that we have a pest with several enemies as shown in Figure 2. Now stability requires that all the predators except possibly one of them must be self-damped. The impact of a change in a predator in the pest is equal to its link to the pest times the complement, which is the product of the self-damping of all the other predators, divided by the feedback of the whole system. Let aii be the self damping of predator i, and let pi be its predation rate on the pest.
Let A =(-1)k times the product of all the aii divided by the feedback of the whole system, where k is the number of predator species. The effect of any predator i is then pi A/aii. That is, it is proportional to the intensity of predation but inversely proportional to the self-damping of that predator. Entomologists usually look only at pi to determine the most effective predator. This is why what seemed like a reasonable decision sometimes fails. Self-damping reduces the effectiveness of a predator. Therefore we have to explain self-damping.
POPULATION GROWTH: SELF DAMPING
Every species population is regulated directly or indirectly by its density. Single-species models of population growth of the form  would result either in unlimited growth if r > 0 or collapse to extinction if r is negative.
would result either in unlimited growth if r > 0 or collapse to extinction if r is negative.
Therefore the logistic model was introduced:
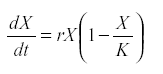
where K is the carrying capacity of the environment for that species (28). Other forms of self-regulation are possible. They all require that either reproduction decreases or mortality increases with numbers. The regulation may be indirect, by way of the depletion of resource or because population growth increases its predator.
Self-damping may occur by way of migration as follows. Suppose that a population in a given area grows according to:

where m is the immigration. Then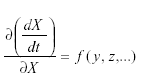 But at equilibrium,
But at equilibrium,  so that
so that 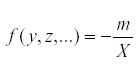 . Therefore
. Therefore 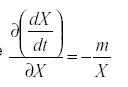
That is, the self damping is inversely proportional to the immigration as a fraction of the total population. A highly mobile species that is derived mostly from outside the field we are trying to protect will be less effective that one whose population is self-contained, reproducing within the field.
A second source of self-damping occurs when mortality increases with numbers. This may occur when the prey attracts its enemies, and an aggregation of prey will be especially vulnerable. A population will be considered aggregated if it clusters more than would be expected from a Poisson distribution. This may come about because some feeding sites are more attractive than others or because the insect does not move very much. In the case of insects which are sessile after the initial instars such as scale insects, aggregation is a consequence of offspring remaining near each other. It is measured, after Taylor by the coefficient b in the equation log(M) = a + b log(V) (27).
Where M is the mean number of insects per leaf and V is the variance. The parameters a and b are estimated from the data. For a Poisson distribution b=1, indicating random distribution. In most cases studied, 1 < b <2 indicating aggregate patter disposition.
In work with the scale insect Lepidosaphes gloverii on Valencia oranges we found that after the crawler stage the females show an aggregated distribution that decreases with instars as a result of differential parasitism when more scales are present (12). Mortality as measured by the fraction parasitized by fungi or a parasitoid increases with the number of scales on a leaf.
- When should we maintain populations of the pest in order to assure the presence of the enemy?
A predator may have alternate prey. Then the complement of the herbivore is the two-species feedback loop as shown in the Figure 3. A generalist predator with alternative prey acquires self-damping from the prey and therefore is less effective in biological control than a predator which specializes on the pest and responds more strongly to its population growth. This can lead to the paradoxical result that a predator with a greater predation rate may be less important in regulating a pest than one with less predation but also very much less self-damping.
The old manuals of “plant hygiene” called for the cleaning of the spaces between fields and the elimination of any weeds or potential alternate hosts for the pest (30). However if a pest is absent its specialized parasitoids will not be present either and there will be a delay between the arrival of the pest and its enemy during which the pest might increase rapidly and harm the crop. Therefore it has been suggested that we need an alternative host in order to keep the natural enemies available.
Since we have common sense arguments for opposite actions, a model is required to decide between them. Figure 4 shows a situation in which there are two plant species. P1 is the crop that we want to protect and P2 is an alternative host for the pest. H1 is the population of the pest herbivore on the crop and H2 is its population on the alternative. N1 and N2 are the populations of natural enemy on the crop and the alternative host. Both the herbivore and the enemy can move back and forth between the two plant species. We are interested here in the impact of an increase in P2 on P1. There are two pathways: from P2 to H2 to H1 to P1 is a negative pathway. Pests on the alternative host also increase the number of pests on the crop.
This process leads to the traditional recommendation to eliminate P2. Its complement in the graph is the loop (N1, N2). The natural enemy may or may not have self-damping, but the movement itself does not: migration between the two plant hosts by itself would give:

so that the net feedback from migration alone in the subsystem (N1,N2) is -the determinant of the first partial derivative:
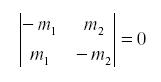
Of course the natural enemy may be self-damped for other reasons. If not all emigrants reach the other host, we might have:
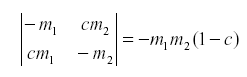
where c is the fraction of the emigrants that fail to reach the other host due to mortality during movement or leaving the area.
Therefore maintaining an alternative host will be beneficial for the crop if the natural enemy has little or no self-damping. In either case, the natural enemy will increase on both hosts when its prey increases on either one.
MODELS OF PLANT PRODUCTION
In some cases it is useful to model the growth of the crop independently of the pests.
Fruit trees. The yield of a fruit tree depends on the conversion of the products of photosynthesis into harvestable fruit instead of being lost to respiration or consumed by herbivores. Therefore the dynamic is one of producing a soluble photosynthate and its removal. During the growing season the leaf mass of the tree does not change much, so we can represent it by the production of the usable materials, R, at rate a. Then we may have:
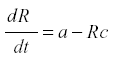
where a is the rate of production and c the rate of conversion into fruit. The accumulation of fruit is then equal to the sum or integral of Rc during the period when fruit is formed. The average rate of formation of fruit is E{Rc}. R reaches an equilibrium level at a/c, and the yield is simply a. Now suppose that some of the photosynthate is consumed by respiration or other plant uses. Then we can change the model to 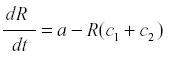
where c1 is the rate of diversion of R to other uses and the rate of fruit formation. Now R reaches a steady state at -------------- and the yield is  . and de yield is
. and de yield is 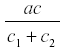
Now we introduce the herbivore H:
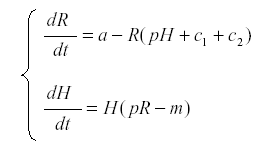
where p is the rate at which the herbivore consumes nutrient and uses it for reproduction, and m is the mortality of the herbivore. The first surprising result is that R now reaches an equilibrium at 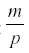 , independent of a, and the harvest is
, independent of a, and the harvest is 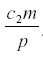 . Neither c1 nor a enter into the result, but the harvest depends directly on the herbivore’s parameters of consumption and fecundity and the death rate. The herbivore equilibrium population is
. Neither c1 nor a enter into the result, but the harvest depends directly on the herbivore’s parameters of consumption and fecundity and the death rate. The herbivore equilibrium population is 
Here c1 and c2 depend on the tree and can be influenced by fertilizer and the weather.
Notice that the physiological efficiency of the tree in using nutrients reduces the herbivore population. Finally, p is the feeding rate (here we merged it with herbivore reproduction but it need not be so). We can ask, what is the relative importance of herbivore reproduction and mortality in yield and of plant parameters on the herbivore population? If we slow down herbivore feeding and reproduction, will that offer more protection than increasing its mortality? This model can be criticized from many points of view. The plant parameters may depend on the weather and therefore not be constant, or some of the photosynthate may go into vegetative growth that increases a. Other models may be introduced to capture the specific problems of different fruit crops (Figure 5). The qualitative result here is that under herbivore pressure, control of the crop passes from plant physiology to the herbivore dynamics.
- Pasture
Tillman and his colleagues have examined the population dynamics of perennial grasses in which new growth is inhibited by previous growth (31). Other author studied a number of models to capture this dynamics (17, 30). The variable was plant biomass from one year to the next. Therefore a difference equation is the appropriate method. The grass next year, xn+1, consists of the survival of grass from this year and new growth. Suppose that a fraction a of this year’s grass survives (a<1). Suppose further that new growth is proportional to b from underground roots, but only occurs in microsites without previous plant cover. Suppose that s is the probability that a microsite is shaded by a unit of grass . Then 1-s is the probability that it is not shaded, and (1-s)x is the probability that it is not shaded by any of the x units of grass in that patch. Therefore new growth is b(1-s)x(n) or be-xln(1-s). Substitute for convenience r=-ln(1-s). This gives a plausible equation x(n+1) = ax(n) + be-rx(n).
Since ln(1-s) is negative, multiply the equation by –ln(1-s) and let y(n) = -x(n)ln(1-s). Then we are left with the resulting equation y(n+1) = ay(n)+rbe-y(n).
Difference equations can be simulated more easily on a computer than differential equations.
The interesting result of this analysis is that if 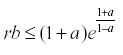 then the equation has a stable equilibrium.
then the equation has a stable equilibrium.
If 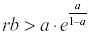 then y, and therefore x, will oscillate from year to year even under constant environmental conditions.
then y, and therefore x, will oscillate from year to year even under constant environmental conditions.
Here r reflects scaling and constant properties of the grass. The result means that if the quantity of grass is dominated by carry over from the previous year then it will be stable, but if it is dominated by new growth the system may oscillate. Since herbivores can affect survival of grass or new growth (for instance if they attack the meristematic buds), herbivores may act either to stabilize or destabilize the pasture. Grazing intensity acts on grass survival, a. Greater grazing pressure reduces a and makes it more likely that the pasture will oscillate.
Other models make use of different equations but they all have in common that the reproductive rate of grass decreases with grass abundance. Some models also make survival sensitive to grass levels. We can also allow the litter of this year’s grass to inhibit new growth, but last year’s grass may have decayed already and released nutrients so that we have a delay equation such as y(n+1)= ay(n) + (b+cy(n-1))e-y(n).
A graphical approach to a difference equation could be carried out using the procedures of the web map.
THE WEB MAP
A scalar difference equation xn+1 = f(xn) can be visualized graphical as follows. Plot xn+1 as a function of xn in the positive quadrant. Draw the 45o bisector of the quadrant. The equilibrium point is the intersection of the bisector with the function. Start from any value of xn-1 along the xn-1 axis, and draw a vertical line to the function. Then draw a horizontal line to the bisector. This gives us the next value, xn+1. Repeat the process: vertical line to the function, horizontal to the bisector. Successive iterations generate the trajectory of a solution of the equation. It may approach equilibrium monotonically or in an oscillatory fashion or move into periodic or chaotic trajectories depending on the equation. If f(xn) is the peak( or trough) of the function, xn+1 gives the maximum (or minimum) of the permanent region of the solution and the next iteration gives the minimum (or maximum). These bounds together give the region of permanence. If a solution starts in the region of permanence it will always remain in that region, and if it starts out that region it will enter the permanent region within three semi-cycles for models with a single extremum.
The nature of solutions of the scalar difference equation depends on the shape of the function. If the slope of f(xn) is between -1 and 1 at equilibrium, the equilibrium is locally stable, while if the slope is outside that range it is unstable. A periodic solution is stable if the product of the slopes around the periodic solution lies between -1 and 1. If all periodic solutions are unstable and the solutions are bounded then we have chaotic behavior. Chaos fits into the analysis of semi-cycles as follows. After finding the peak, maximum and minimum of the function (thus giving us the region of permanence), we find the pre-images. The first pre-image is the root other than equilibrium of f(pre-1) = x* where x*is the equilibrium. The second pre-image is the solution of f(pre-2) = pre-1 and so on. This divides the interval (0,¥) into segments bounded by the pre-image
If Pre-1 <xn <x* Then xn+1 >x*.
If Pre-2 < xn < Pre-1 Then Pre-1 <xn+1 <x*, and so on.
If Pre-(k+1) < xn <Pre-k Then Pre-k < xn+1 < Pre-(k-1).
The pre-images may fall outside the region of permanence. The maximum semi-cycle length in the permanent region is k if k is the highest pre-image within the region of permanence. Thus we can find the maximum semi-cycle length from the number of pre-images on each side of equilibrium. From a theorem by Li and Yorke (20) we see that if pre-2 is in the permanent region then the equation is chaotic. That is it has periodic solutions of every period and non-periodic solutions near them, and shows extreme sensitivity to initial conditions. Yet even for chaotic equations the semi-cycle lengths are limited by the number of pre-images in the permanent region. Whereas the stability of local equilibrium and periodic solutions depends on the slopes at the equilibrium points, chaotic properties depend on the shape of the function, the relative positions of the landmarks peak, equilibrium, maximum, minimum, and the first two pre-images (18,19).
In order to understand how the shape of the curve determines the behavior of the solution of the equation, we can construct a difference equation out of line segments. If we use only two line segments, the first one has to have a slope greater than 1 in order for there to be a positive equilibrium. If the second segment has a slope >-1, the equilibrium is locally stable while if it has a slope <-1 the equilibrium is unstable and the equation is chaotic. A more interesting situation arises when we use more line segments. Choose the initial point for each segment bi and the slope of that segment, si.
Then the function g(x) has the piece-wise continuous non-delay difference equation:
Xn+1 =g(Xn).

The relation of equation of g(x) is here taken to be a series of six line segments. The segments break at the points b0 ,b1,… b6 . The parameters si are the slopes of the segments, and the ci the heights of the curve at each breakpoint. We first set the bs. Then we have the choice of working with the heights (cs) or the slopes s. Whichever we choose, the other is then determined.
This model is only a rough representation of real relations between successive populations. The discontinuity of the slope at the breakpoints does not cause any trouble, but the peak in these models is abrupt, without necessarily passing through a flat region of zero slope the way a continuous f(x) would. That limits possible outcomes.
The power of this model is that we can alter the shape of the curve in sections and therefore discover what we mean by “shape”. We can keep the same equilibrium point but change the steepness of the slope around equilibrium, or change the height of the function and therefore its maximum. By choosing s1 to be positive, s2, negative, s3 positive, s4 negative we produce a two-peaked function. This representation is used to find the consequences of different interventions. Suppose for instance that we use some economic threshold to trigger and intervention. If the threshold is above equilibrium for the pest population, increasing mortality by our intervention makes the slope steeper. It does not affect equilibrium or the pre-images but maskes the minimum value smaller. Therefore it can bring pre-2 out above the minimum, into the permanent region, and result in chaotic behavior. An intervention which increases pest mortality when it is rare can preserve stability. Stability is not necessarily desirable nor chaos undesirable, but the dynamic impact of our activity has to be understood.
What if we do not have observations on the predator?
If we have a pair of equations in two variables, we can sometimes solve for one of the variables in terms of the other. This gives us an equation of higher order but in one variable. Thus consider for example the pair of equations for an herbivore and its predator:
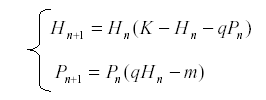
Suppose that we have a long series of observations for H but not for P. Then we can solve equation for P:

and adjusting subscripts to the conventional form we end up with:

This is now a second order equation but only in H, the observed variable. Statistical methods can estimate the parameters k, q and m. Thus we can find the predation rate and mortality of the predator even without knowing its identity. But once we have estimated the mortality m, its reciprocal estimates the life expectancy of the predator. If m is large, say 0.14 per day, the life expectancy is on the order a week, and we can suspect the predator is a mite, whereas if m is 0.01 and life expectancy is 100 days we can look for a larger enemy.
CELLULAR AUTOMATA
All of the above models treated the herbivore/enemy dynamics at a point, without considering space except as migration rates. But a farming region is a patchwork of habitats, each with its herbivore and enemy populations and linked by migration. Cellular automata is a simulation procedure in which we assign initial conditions and parameters to each patch and examine the spread or containment of a pest (4). The patches may be of different kinds. For instance in the case of the bean golden mosaic virus and its whitefly vector, a patch may have a crop which is or is not vulnerable to the virus, suitable or not suitable for whitefly feeding or reproduction, open to whitefly movement or an obstacle. Planting may occur on different dates in the different patches. Clearly this would be too complicated for analytic methods except in extremely simplified cases so that simulation is the preferred technique. After assigning patch characteristics according to the crop and date, we have equations for each variable in each patch and the migration pattern among them. In each iteration the internal dynamics within a patch and the migrations among them give the values for the next time period.
The model may set up according to two strategies. The first strategy takes a real region with its crop pattern and attempts to simulate the process of outbreak, damage and decline of pest. Our own interventions appear as factors influencing mortality and migration in each crop. Usually the outcome we want to measure is the damage caused when we manage the system in different ways.
The second strategy poses theoretical questions. For instance, if fields are homogeneous in blocks of patches, how do the size and shape of the patch affect the outcome? What is the effect of partial barriers to movement?, of staggered planting dates?, of unexpected weather? What is the vulnerability of the system to unexpected conditions or errors of intervention? These studies do not apply to any particular place but establish principles that can then be tested in models of individual farms or farming regions.
CONCLUSIONS
1. Qualitative and semi-quantitative models in agricultural ecology are useful for understanding the dynamics of even moderately complex systems where common sense alone can often be misleading. It can help decide between alternative explanations, explain puzzling phenomena and guide decisions about intervention. They also point to situations where further quantification is needed and suggests when to use computer simulation.
2. Some models are suggested such as:
a) When only herbivore is self-damped, if two signs along a row are the same, the variables will show a positive correlation when environmental change enters the system by way of that variable, and if the signs are opposite there will be a negative correlation. Increased food supply does not change the population of herbivores because increased reproduction is compensated for by increased predation, but the population is younger and possibly of larger individual size.
b) When an herbivore with more than one enemy, one of which is not self-damped, it shows that the impact of a predator is proportional to its predation rate but inversely proportional to its self-damping. Therefore, the self-damping is an object of research.
c) When a predator has more than one prey, any change that reduces one prey species reduces the predator and therefore increases the other prey population. Thus the two preys interact as if they were competitors, but indirectly, by way of their common predator. Therefore changes entering the system by way of the prey generate a negative correlation between them and a positive correlation with the predator, while changes originating at the predator level generate a negative correlation between the predator and both prey and a positive correlation between the prey.
d) When is advisable to maintain a pest on some alternate host in order to maintain a specialized parasitoid, the answer depends on whether the predator is self-damped as a two variable system (the self-dasmping from movement between crop and weed cancels itself out). If the self-dsamping of the predator is strong, the symbol a in the table is positive. The symbol b is positive if migration of the predator between weed and crop is stronger than the indirect effect by way of predation and migration of the pest.
3. For the analysis of logistical growth in the population, the work sheet includes the samples of the density, some economic threshold and parameters to increase natality or mortality. In the model, population growth follows the familiar logistic when the population is below the threshold b, and then survival decreases by an additional exponential factor. Since in this model the threshold is above equilibrium it has no effect on the equilibrium value itself or the maximum, but lowers the minimum to values below of the equilibrium. Therefore although it can reduce the average population of the pest it results in increased fluctuation with occasional higher peaks. If the equilibrium is stable, it will eventually be captured by the equilibrium. But meanwhile new perturbations can displace the population from equilibrium and it will continue to fluctuate.
REFERENCES
1. Awerbuch T, González C, Hernandez D, Levins R, Sandberg S, Sabat R, Tapia JL. The natural control of the scale insect Lepidosaphes gloverii on Cuban citrus. Red International de Cítricos (IACNET). 2003;21(22):40-41.
2. Awerbuch T, Levins R, Predescu M. The role of seasonality in the dynamics of deer tick populations. Bull Math Biol. 2005;(67):467-486.
3. Bernstein C. A simulation model for an acarine predator – prey system (Phytoseiulus persimilis – Tetranychus urticae). J Anim Ecol. 1985;(54):375–389.
4. Carroll M. Quantitative estimates of time-averaging in brachiopod shell Accumulations from a Holocene Tropical Shelf. Thesis submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial fulfilment of the requirements for the degree of Master of Science in Geological Sciences. Brazil; 2001.
5. Cué JL, Castell E, Hernández JM. Estadística. Segunda Parte. Universidad de La Habana, Facultad de Matemática–Cibernética. Editorial Ciencia y Educación;1987.
6. Chen W, Wang M. Non-constant positive steady-states of a predator-prey-mutualist model. Chinese Annals of Mathematics. 2004;25(2):243-255.
7. DeVault R, Grove EA, Ladas G, Levins R, Puccia C. Oscillation and Stability in models of perennial grass. Dynamic Syst and Applications. 1994;(1):87-94.
8. Dambacher JM, Levins R, Rossignol Ph. Life expectancy change in perturbed communities: derivation and qualitative analysis. Math Biosciences. 2005;(197):1-14.
9. Dreyer TP. Modelling with ordinary differential equations. CRC Press Florida; 1993.
10.Fleming ChM, Robert A. Single species versus multiple species models: The economic implications discussion; 2002. (Consultada: 16 jun 2006). Natural Resource and Environmental Economic 23. Centre for Applied Economic and Policy studies. Department of Applied and International Economic. Massey University, Palmerston North New Zealand. Disponible en: http://econ.massey.ac.nz/caps/s4pub23.pdf.
11.García-Marí F, González JE, Orenga S, Saques F, Laborda R, Soto A, Ribes A. Distribución espacial y asociación entre especies de ácaros fitófagos (Tetranychidae) y depredadores (Phytoseiidae) en hojas de fresón. Bol San Veg Plagas. 1991;(17):401-415.
12.González C, Caceres S, Gómez M. Lepidosaphes gloverii (Hemiptera: Diaspididae), Estudios Biológicos y Ecológicos en Cítricos de Cuba. Rev Soc Entomol Argent. 2005;64(1-2):26-28.
13.Huffaker CB, Van der Vrie M,McMurtry JA. Ecology of Tetranychid mites and their natural enemies. Hilgardia. 1999;27(14):343-383.
14.Hui J, Chen LS. Existence of Positive Periodic Solution of Periodic Time-Dependent Predator-Prey System with Impulsive Effects. Acta Mathematica Sinic. 2004;20(3):423-433.
15.Hume F, Hindell M, Pemberton D, Gales R. Spatial and temporal variation in the diet of a high trophic level predator, the Australian fur seal (Arctocephalus pusillus doriferus). Marine Biology. 2004;144(3):407-416.
16.Jonson M. Biological control of pest. Entomol Argent. 2000;67(1):53-65.
17.Lau FCM, Tam WM. Novel SIR-Estimation-Based Power Control in a CDMA Mobile Radio System Under Multipath Environment. Transactions on Vehicular Technology. 2001;50(1):314-321.
18.Levins R. Models for regional heartwater epidemiology in a variable environment. J Vet Res. 2000;(67):163-165.
19.Levins R. Sorpresas, errores y dudas. Revista Cubana de Salud Pública. 2004;30(3):225-232.
20.Li TY, Yorke J. The “simplest” dynamical system. Dynamical Systems. 1976;(2):203-206.
21.MacDonald R, Marsch IW. Currency forecasters are heterogeneous: confirmation and consequences. J International Money and Finance. 1996;21(5):460-469.
22.McDonald BA, Menon S. Direct Numerical Simulation of Soild Propellant Combustion in Cross –Flow. J Propulsion and Power. 2005;21(5):460-469. (Consultada: 16 jun 2006). Disponible en: http://www.ccl.gatech.edu/papers/paper_info?pub_id=275.
23.Mckenzie EF, Samba EM. The role of mathematical modelling in evidence-based malaria control. J Tropical Medicine and Hygiene. 2004;71(2):94-96.
24.Piccardi C, Lazzaris S. Vaccination policies for chaos reduction in childhood epidemics. Transactions on Biomedical Engineering. 1998;45(5):591-596.
25.Prusinkiewicz P, Hammel J, Mech R. Visual models of plant development. Handbook of formal languages. 1997;(3):535-597.
26.Rabbinge R, Ward SA, Van Laar HH. Simulation and systems management in crop protection. Editorial Center for Agricultural Publishing and Documentation (Pudoc), Wageningen, Netherlands; 1989.
27.Rabinovich JE. Introducción a la ecología de poblaciones. 2da edición. Editorial Continental. México; 1989.
28.Sharov AA. Course Quantitative Population Ecology. Department of Entomology Virginiatech, Blacksbug; 1999. (Consultada: 16 jun 2006). Disponible en: http://www.ento.vt.edu/sharov/pop ecol/.
29.Snedecor GW, Cochran WG. Métodos estadísticos. Compañía Editorial, S.A. México;1971.
30.Sterner R, Bajpai A, Adams T. The enigma of food chain length: Absence of theoretical evidence for dynamic constraints. Ecology. 1997;78(7):2-4. (Consultada: 16 jun 2006). Disponible en: http://www.findarticles.com/p/articles/mi_m2120/is_n7_v78/ai_20417944/pg_2.
31.Tillman C, Vogel S, Ney H, Zubiaga A. A d-p based search using monotone alignments in statistical translation. In: Proceedings of the 35th Annual Meeting of the Association for Computational Linguistics. Madrid, Spain; 1997.
32.Von Bertalaffy L. Teoría general de los sistemas, fundamento, desarrollo, aplicaciones. Décima impresión, Fondo de cultura económica, UNAH. La Habana; 1995.
33.Wang Y, Waibel A. Decoding algorithm in statistical machine translation. In: Proceedings of the 35th Annual Meeting of the Association for Computational Linguistics. Madrid, Spain; 1997.
34.Wilson LT, Booth DR, Morton R. The behavioural activity and vertical distribution of the cotton harlequin bug Tectocoris diophthalmus (Thunberg) (Heteroptera: scutelleridae) on cotton plants in a glasshouse. J Aust Ent Soc. 1983;(22):311-317.
35.Williams DW, Liebholds AM. Detection of delayed density dependence: comment – comments. Ecology. 1995;(76):1005-1008.
36.Yan NX, Rong X, Lan Sun Ch, Rong X. Global Stability of a Predator-Prey System with Stage Structure for the Predator. Mathematic. 2004;20(1):63-71.
(Recibido 23-3-2006; Aceptado 16-6-2006)














