My SciELO
Services on Demand
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Biotecnología Aplicada
On-line version ISSN 1027-2852
Biotecnol Apl vol.31 no.1 La Habana Jan.-Mar. 2014
RESEARCH
Stoichiometry equation to describe the growth of the Pleurotus ostreatus ceba-gliie-po-010606 strain
Ecuación estequiométrica para describir el crecimiento de Pleurotus ostreatus cepa ceba-gliie-po-010606
Julio A Pineda-Insuasti1, Claudia P Soto-Arroyave2, Luis Beltrán3
1 Centro Ecuatoriano de Biotecnología del Ambiente, CEBA. Ibarra, Imbabura, Ecuador.
2 Pontificia Universidad Católica del Ecuador, PUCESI. Ibarra, Imbabura, Ecuador.
3 Departamento de Ingeniería Química, Universidad Ignacio Agramonte Loynaz. Camagüey, Cuba.
ABSTRACT
This work was aimed at developing a proximate stoichiometric equation to describe the growth of Pleurotus ostreatus mushroom strain ceba-gliie-po-010106 on picking beans (Phaseolus vulgaris) waste. Empirical formulas were established for the residue of fresh dried picking beans (CH1.81O0.81N0.15) and the biomass of the fungal strain (CH1.83O0.84N0.26). The elemental composition of these materials and the ashes was determined. The stoichiometric coefficients obtained further supported the estimation of parameters relevant for fungal growth characterization: theoretical biological efficiency (867.49 g of fungal dry matter (FDM)/kg of substrate dry matter), mean coefficient of breath (0.77 CO2/mol O2 consumption), specific air consumption (1.36 m3/kg FDM) and metabolic heat (16 576.47 kJ/kg FDM).
Keywords: Pleurotus ostreatus, solid fermentation, edible fungus, stoichiometry.
RESUMEN
Se desarrolló una ecuación estequiométrica aproximada que describe el crecimiento de la cepa ceba-gliie-010106 de Pleurotus ostreatus sobre residuos de la cosecha del fréjol (Phaseolus vulgaris). Se establecieron fórmulas empíricas para el residuo del fréjol fresco seco (CH1.81O0.81N0.15) y la biomasa de la cepa del hongo (CH1.83O0.84N0.26). Para ello se determinó la composición elemental de estas materias primas y su contenido de cenizas. Los coeficientes estequiométricos permitieron estimar parámetros relevantes del proceso de crecimiento; entre ellos: la eficiencia biológica teórica (867.49 g de materia seca del hongo (MSH)/kg de materia seca del sustrato), el coeficiente medio de respiración (0.77 mol CO2/mol O2), el consumo específico de aire para el proceso de crecimiento (1.36 m3/kg MSH), así como el calor metabólico (16 576.47 kJ/kg MSH).
Palabras clave: Pleurotus ostreatus, fermentación sólida, hongo comestible, estequiometría.
INTRODUCTION
The Earth produces an estimate of 146 billion tons of living matter, known as Biomass, yearly [1]. Those resources have a great potential to face the challenges of decreased availability of traditional non-conventional fuels sources and to prevent the risks to stable food supply in most countries.
One of the possible ways to take advantage of those wastes is to use them for edible fungi production [2]. A quarter of all the cereal wastes annually discarded could be used to produce fresh edible fungi, enough for a daily supply of 250 g to more than four million people [3]. There is a very significant increase in mushroom and truffles production worldwide. According to the analysis by Toland and Lucier [4] on the data provided by the United Nations Food and Agriculture Organization (FAO), the worldwide production of that food rich on proteins and nutrients have exponentially raised from 1961 to 2009, and it duplicates every 13.02 years. Pleurotus ostreatus, also known as oyster mushroom, is one of the most extensively cultivated mushrooms either in warm or hot climates. However, mushroom cultivation techniques are mostly empirical and many of the methods remain unpublished or are protected by several patents [5-14]. Therefore, mechanistic approaches are demanded to develop more efficient biological processes for that purpose [15]. Such procedures comprise the expression of process’ mathematical models and implementing optimization procedures based on computational modeling [16]. In this sense, process design has become a mathematical programming task, being identified by several authors as a design in transit from in vitro to in silico [15, 17, 18].
One of the primary contributions to bioprocess modeling comes from identifying a stoichiometric model by establishing the mass relationships among the main raw materials [19]. These models results in, either, a simplified analysis expressed in terms of a global stoichiometric equation describing the process from a non-structured perspective, or more complex ones, with a system of several equations describing the balances of cellular metabolism and cell-culture medium interactions [19, 20].
Following this strategy and after an unsuccessful exhaustive review of the literature on this topic, we decided to develop a stoichiometric equation to describe the growth of the P. ostreatus basidiomicete on industrial wastes. Thus, a stoichiometric equation was obtained, describing the growth of the P. ostreatus Ecuadorian strain ceba-gliie-po-010106 on picking beans’ harvest waste.
MATERIALS AND METHODS
Strain
The P. ostreatus Ecuadorian strain ceba-gliie-po-010106 was provided by the Ecuadorian Center of Environmental Biotechnology (CEBA). It was preserved in Agar-Malt extract at 4 ºC until use.
Raw materials
Two raw materials were used to develop the empirical formulas: picking beans (Phaseolus vulgaris) harvest wastes, the entire plant, and the P. ostreatus biomass. Picking beans waste samples were used as primary raw material, being collected from the production communities La Concepción, Salinas and Ambuquí at the Imbabura and Carchi provinces (Figure).
Fresh picking beans waste sampling procedure
Both, the picking beans waste and the mushroom biomass were sampled following the procedures described by Oakland [21]. For three months, three 14-kg samples of picking beans waste were collected every month, sun-dried after harvesting, for a total of 9 samples. The procedure used for monthly processing is described in the following. The three samples were separately grinded to a 9-mm size in a hammer hog and further mixed. The mix was extended on the floor in a 4 m2 square area. The square was divided in four even quadrants, and a 1 kg portion of the mix was collected from each quadrant, and further grinded with a manual grinder down to a 1 mm in size. It was extended again in the floor in a 1 m2 square area, divided in four even quadrants. Samples of 25 g were collected from each quadrant and mixed for a final sample of 100 g for each month. Samples were packed in polystyrene bags and stored at 4 ºC during the sampling period (Figure).
P. ostreatus biomass sampling procedure
The monthly-harvested picking beans waste was used for mushroom production at the CEBA production plant. The biomass produced by the three first sprouts of the fruiting body was stockpiled, during 51 days. After that time there was no significant mushroom growth. The growth medium for fungal biomass production was used without nutrient supplementation. Three samples 1-kg each were harvested every month, for a final amount of 9 kg. The mushroom biomass obtained every month was dried until constant weight in an oven at 70 ºC. It was further grinded in a manual grinder and extended on a 1 m2 square table, which was subdivided in four even quadrants, and 25 g were collected from each quadrant and mixed to homogeneity. The final sample of 100 g was stored at 4 ºC during the sampling period. Three samples 100 g-each were obtained.
Biomass culture procedure by solid fermentation
The picking beans waste samples were grinded down to 9 mm in size and the humidity was set to 70 %. Polypropylene bags were filled with 300 g of substrate and further pasteurized in a sterilizer at 103.46 kPa for 30 min. When the substrate reached room temperature, it was inoculated with 4 % dry base. Samples were incubated at a constant temperature of 20 ºC for 51 days. The relative humidity was kept at an average of 85 % to avoid hyphal contamination, and after the sprout of the first primordium, it was raised to 90 %. Fifteen days later, the mushroom was harvested, with an average size of 8 cm. The experiment was conducted with three bags as replicates.
Elemental composition analytical technique
Samples were analyzed at the Center of Research Services and Chemical Analyses (CISAQ), of the National University of Loja, Ecuador. The elemental analysis was done with a PerkinElmer, model 2400, series II equipment [22]. This technique provides the total content of carbon, hydrogen, nitrogen and sulfur for a wide range of samples either organic or inorganic, solid or liquid, by using the Pregl-Dumas’ classical method [22, 23]. This method consists on the combustion of a sample of known mass at high temperature (approximately 900 ºC) in the presence of pure oxygen. The process releases carbon dioxide, water and nitrogen. The gasses are passed through special columns which absorb the carbon dioxide and water. A column carrying a thermal conductivity detector separates the nitrogen from any carbon dioxide or water residue, and the resulting nitrogen content is measured. The instrument must be previously calibrated by analyzing a pure standard of known nitrogen content. Then, the signal of an unknown nitrogen concentration sample is measured by the thermal conductivity detector, and converted into the equivalent nitrogen content value [24, 25].
Calculation of raw materials empirical formulas
Data corresponding to carbon, hydrogen, nitrogen and sulfur were obtained from fresh picking beans waste and mushroom fruiting body biomass by the technique previously described. Oxygen content was calculated as the remaining elemental composition difference, in disregard of other elements present in significant amounts. Elements’ concentrations in the solid phase were determined for the organic fraction once subtracted the ashes present in the sample. These data were used to calculate the relative atomic mass ratio for each element, by the ratio of the element’s mass fraction over its atomic mass. The atomic mass ratio could be deduced from these relative atomic mass ratios, by dividing each element value over that of carbon, the final value being expressed per carbon atom-gram. The empirical formulas of the raw materials used on this work do not include sulfur, due to its very low proportions and, therefore, its irrelevance for stoichiometric balances.
Proposal of a simplified stoichiometric model
It started from considering the aerobic cell growth as a simplified mechanism, expressed through a simplified stoichiometric equation. It describes the transformation of fresh picking beans substrate, together with a nitrogen supplement in form of ammonia and oxygen as reactants, into products due to the presence of the mushroom as biocatalyst. The resulting reaction products considered were the P. ostreatus biomass, CO2 and water:
![]()
The stoichiometric coefficients were determined from a balance per element from equation (1) [19]:

Where:
α, β, γ, δ and ε are stoichiometric coefficients expressed as moles of the respective compound per mol of fungal dry matter (mol/mol FDM).
xi: hydrogen content on the molecule per carbon atom-gram.
yi: oxygen content on the molecule per carbon atom-gram.
zi: nitrogen content on the molecule per carbon atom-gram.
There were only five equations available for 5 variables; hence, another equation was required. A recommended alternative for this scenario is the electron balance [19, 26]. It implies to calculate the reduction degree of the species involved (λ). This factor is defined as the number of moles of electrons available per carbon atom-gram to be transferred to O2, during the full combustion of a given compound to render CO2, H2O and N2. For carbon, 4 electrons are free electrons to be transferred, with 1 for hydrogen, -2 for oxygen and -3 for nitrogen [19]. Positive and negative values stand for electrons either to be donated or accepted, respectively. Accordingly, the reduction degree for CO2, H2O and NH3 is null. An electron balance from equation (1) leads to the following expression:
![]()
Where: λFF and λXV are the reduction degrees of fresh picking beans waste and mushroom biomass (electrons/mol).
In this way, equations (2) through (6) form a system of linear algebraic equations with a single solution for each variable.
Parameters derived from the stoichiometric equation
Relevant factors related to mushroom biomass production can be derived from the stoichiometric equation (1), such as: theoretical biological efficiency (BE), mean coefficient of breath (CB; mol CO2/mol O2), specific volumetric air consumption (qAir) and the metabolic heat (-∆HM):
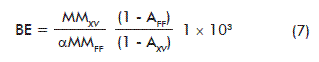
Where:
BE: biological efficiency (g FDM/kg SDM)
SDM: substrate dry matter
MMXV: molecular mass of the ash-free biomass (g/mol)
AFF: ash of fresh picking beans waste (g/mol)
MMFF: molecular mass of the ash-free fresh picking beans waste (g/mol)
AXV: biomass ashes (g/mol);

Where:
qAir: volumetric specific air consumption (m3/kg MSH)
MMO2: oxygen molecular mass (g/mol)
yO2: air oxygen fraction (mol O2/mol total);
ρAir: air density (kg/m3)
![]()
Where RC is the respiration coefficient
According to Ertola et al. [19], the heat released during the metabolic process is proportional to the number of electrons to be transferred to oxygen during the reaction [27]. The mean value (Q0) deduced from a large number of reactions was 115.137 kJ/electron. Following these results and also based on a dimensional analysis, the metabolic heat was calculated and expressed in kJ/kg FDM by the equation:
![]()
Where:
(-ΔHM): stoichiometric metabolic heat (kJ/kg FDM).
λFF: reduction degree of the fresh picking beans waste (electrons/mol).
Results computed for parameters of equations (7) through (10) depend on the results obtained once calculated the remaining variables on equation (1). They include those of the empirical formulas for the substrate and the biomass, and also the stoichiometric coefficients.
RESULTS AND DISCUSION
Determining the empirical formulas for biomass of the fresh picking beans waste and the P. ostreatus mushroom is highly relevant to establish the stoichiometric equation describing the growth of the selected P. ostreatus strain, and also for the stoichiometric equation balance and the calculation of its coefficients. Table 1 summarizes the elemental composition and the estimated values for relative atomic relationships/ratios of the fungal biomass, starting from measurements of the collected samples.
The P. ostreatus nitrogen levels were among the highest for a biomass tested [28], as expected from a fungal biomass. Instead, carbon levels were low, if we compare them to a list of elemental composition reported for forty agriculture matters [29]. This could explain the relatively high atomic mass ratio calculated for the oxygen, almost twice the value reported for many microorganisms. The ashes content was comparable to the lowest values reported by Sánchez and Mata [30] for eleven edible fungi species, and was closer to that of Pleurotus sajour-caju (5.84 %).
Results for elemental composition and the calculation of relative atomic mass ratios of the fresh picking beans waste, starting from the measurement of collected samples, are shown in table 2.
The chemical carbon composition of the fresh picking beans waste was in the same order of the values reported by Parikh et al. [28] for biomass grown on waste from different sources. According to that group, the carbon content was only higher than those reported for rice hull (40.6 %) and cotton stems (41.3 %). By the contrary, hydrogen and oxygen contents were average compared to equivalent results [28].
Data obtained from empirical formulas for the two highest components, subject of elemental analysis, are shown in table 3. They were used to deduce the process’ stoichiometry. Significant values from table 2 and table 3 were further applied for calculation, in spite of showing just two decimal digit values in the case of the formulas.
There was a marked difference in the elemental composition of P. ostreatus, compared to that reported for Aspergillus niger (CH1.72O0.55N0.17) [31, 32], which was quite more similar to that of the Kluyveromyces marxianus yeast (CH1.94O0.76N0.17) [33]. The elemental composition does not vary for the most dissimilar biomasses; but growth conditions, either nutritional or environmental, are responsible for small variations [28]. This composition places the P. ostreatus strain ceba-gliie-po-010606 with a molecular mass slightly above the mean value established for microorganisms, approximately of 25 g/mol [19].
Calculation of the stoichiometric coefficients
The stoichiometric equation and the balances were established from data shown in table 4 as follows:
![]()
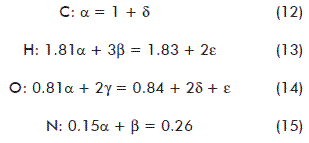
The reduction degree for the solid waste was calculated from data shown in table 3. Data summarized in table 4 was used to calculate the biomass of the fruiting body of P. ostreatus. With this information, the electron balance of equation (6) was set:
![]()
The solution for the system equations (8) through (12) provided the stoichiometric coefficients: α = 1.2689; β = 0.0790; γ = 0.3494; δ = 0.2689; ε = 0.3495. They were used to formulate the stoichiometric equation. Due to its simplicity, only two digits were reported for the stoichiometric coefficients (17):
![]()
Parameters estimated with the stoichiometric equation
Theoretical biological efficiency
Taking into account the amount of ashes and water of picking beans waste, and also that of P. ostreatus biomass, it was estimated that the expected biological efficiency from this system is 867.49 g FDM/kg SDM. This result arises as a model for the efficiency that must be achieved for certain substrates and strain specific conditions. Several authors have optimized the growth medium for different P. ostreatus strains [34]. Otherwise, the maximal efficiency reported for the process at 20 ºC was 261.89 g FDM/kg SDM [35]. Hence, these levels could have been further improved, since they represent just 30.18 % of the estimated theoretical value according to our results. Noteworthy, the biological efficiency depends not only on the attained nutritional balance, but also on other environmental aspects such as: the water retention capacity of the substrate, aeration and the relative humidity at different culture phases, among others [3].
Mean coefficient of breath
As defined for this parameter, the coefficient reached 0.77 mol CO2/mol O2, a relatively low value compared to that reported for the fungal aerobial growth. The breath coefficients commonly derive from increased demands for energy to synthesize the enzyme complexes required to produce simple sugar molecules during growth, as reported for A. niger growth on citric wastes [36]. Another plausible explanation comes from the CO2 retention that occurs in growth bags, which could slightly modify the fungal growth metabolism.
Specific air consumption
The air consumption was calculated for normal temperature and pressure conditions, being estimated as 1.36 m3/kg FDM. This indicator demonstrates that the fungal growth demands a non-significant amount of air to produce a ton of product.
Metabolic heat
According to equations (10) and (17), metabolic heat was estimated as the heat release equivalent to 16 576.47 kJ/kg FDM. A huge amount of energy is normally released in the form of heat during solid fermentation processes due to metabolic activity [37]. This parameter is scarcely estimated by experimentation, being most frequently calculated from stoichiometric balances [38] similar to those developed in our work. For example, González et al. reported metabolic heat values for the growth of A. niger of 16 000 kJ/kg FDM, very similar to ours. This implies that the adjusted stoichiometric equation generates values which are in agreement with those previously reported for fungal growth.
CONCLUSIONS
A proximate stoichiometric equation was developed to describe the aerobial growth of the Ecuatorian P. ostreatus strain ceba-gliie-po-010106 on local picking beans (Phaseolus vulgaris) harvest wastes. Empirical formulas were established to describe the elemental composition of fresh sun-dried picking beans waste (CH1.81O0.81N0.15) and that of the mushroom biomass (CH1.83O0.84N0.26).
The stoichiometry proposed supports the estimation of key parameters for the development of fungal solid fermentation processes, based on mathematical models with a mechanistic approach. They included the theoretical biological efficiency (867.49 g FDM/kg SDM), the mean respiration coefficient (0.77 mol CO2/mol O2), the specific air consumption to grow (1.36 m3/kg FDM) and the metabolic heat (16 576.47 kJ/kg FDM).
ACKNOWLEDGEMENTS
The research resulting on this publication was funded by the National Secretary of Higher Education, Science, Technology and Innovation of Ecuador (SENESCYT), through a Scholarship granted in 2008.
DECLARATION OF CONFLICT OF INTERESTS
The authors declare the absence of conflicts of interests.
REFERENCES
1. Álvarez-Castillo A, García-Hernández E, Domínguez-Domínguez MM, Granandos-Baeza J, Aguirre-Cruz A, Morales-Cepeda A, et al. Aprovechamiento integral de los materiales lignocelulósicos. Rev Iberoam Polim. 2012;13(4):140-50.
2. Chukwurah NF, Eze SC, Chiejina NV, Onyeonagu CC, Ugwuoke KI, Ugwu FSO, et al. Performance of oyster mushroom (Pleurotus ostreatus) in different local agricultural waste materials. Afr J Biotechnol. 2012;11(37):8979-85.
3. Mane VP, Patil SS, Syed AA, Baig MM. Bioconversion of low quality lignocellulosic agricultural waste into edible protein by Pleurotus sajor-caju (Fr.) Singer. J Zhejiang Univ Sci B. 2007;8(10):745-51.
4. Pineda-Insuasti J, Ramos-Sanchez LB. Producción de proteínas comestibles con fuentes alternativas de materias primas. Axioma. 2013;1(10):5-9.
5. Álvaro H, inventor; Garrigues Fongs, S.L., assignee. Procedimiento para la obtención de una composición de un substrato para el cultivo de hongos. Spain patent ES 2 166 337 A1. 2000 Jul 24.
6. Dunn-Coleman NS, Michaels TJ, inventors; Monterey Mushrooms, Inc., assignee. Composting process for the production of mushroom cultivation substrates. United States patent US 4848026 A. 1989 Jul 18.
7. Giovannozzi G, Luigi P, Baldo R, Porri A, D`Annibale A, Perani C, inventors; Consiglio Nazionale Delle Ricerche, Universita' Studi Della Tuscia, assignee. Process for the production of cellulose paper pulps by biodelignification vegetative masses. United States patent US 6379495 B1. 2002 Abr 30.
8. Hisakazu I, Oaza S, Hanishina-Gun N, inventors; Hisakazu Ikeda, assignee. Obtaining edible material fron fungus-digested medium. Europe patent EP 0357320 A2. 1989 Aug 22.
9. Ikeda H, inventor; Ikeda H, assignee. Edible material containing mushroom. United States patent US 5028441 A. 1991 Jul 2.
10. Kok T, inventor; Everbloom Mushroom (Pte) Ltd., assignee. Mushrooms cultivation. Europe patent EP 0248636 A3. 1987 Jun 2.
11. Ladisch M, Kohlman K, Westgate P, Weil J, Yang Y, inventors; Purdue Research Foundation Office of Technology Transfer, assignee. Processes for treating cellulosic material. United States patent US 5846787. 1998 Jul 11.
12. Mee H, inventor; The Kinoko Company, assignee. Method for growing wood mushroom. United States patent US 4127965. 1978 Dec 5.
13. Suryanarayan S, Mazundar K, inventors; Biocon India Limited, assignee. Solid state fermentation. United States patent US 6197573 B1. 2001 Mar 6.
14. Toth E, Toth L, Heltay I, inventors; Licencia Talalmanyokat Ertekesito Vallalat, assignee. Mushroom growing process. United States patent US 3996038. 1976 Dec 7.
15. Kiparissides A, Koutinas M, Kontoravdi C, Mantalaris A, Pistikopoulos EN. Closing the loop in biological systems modeling - From the in silico to the in vitro. Automática. 2011;47(6):1147-55.
16. Rodríguez-Fernández M, Balsa-Canto E, Egea JA, Banga JR. Identifiability and robust parameter estimation in food process modeling: Application to a drying model. J Food Eng. 2007;83(3):374-83.
17. Nfor BK, Verhaert PD, van der Wielen LA, Hubbuch J, Ottens M. Rational and systematic protein purification process development: the next generation. Trends Biotechnol. 2009;27(12):673-9.
18. Lam M. In silico dynamic optimisation studies for batch/fed-batch mammalian cell suspension cultures producing biopharmaceuticals [dissertation]. London: Imperial College; 2009.
19. Ertola R, Yantorno O, Mignone C. Microbiología industrial. Washington: OEA; 1994.
20. Sinclair CG. Cinética de los procesos microbianos. In: Bu'lock JD, Kristiansen B, editors. Biotecnología básica. Zaragoza: Editorial Acribia S.A.; 1991. p. 75-133.
21. Oakland J. Statistical process control. 5th ed. Oxford: Butterworth-Heinemann Ltd.; 2003.
22. Vassilev SV, Baxter D, Andersen LK, Vassileva CG. An overview of the composition and application of biomass ash. Part 2. Potential utilisation, technological and ecological advantages and challenges. Fuel. 2013;105:19-39.
23. Thompson M, editor. CHNS Elemental Analysers Report. AMC Technical Briefs [internet]. 2008 Apr [cited 2013 Jan 6];(29):[2 p.]. Available from: http://www.rsc.org/images/CHNS-elemental-analysers-technical-brief-29_tcm18-214833.pdf.
24. Francis FJ, editor. Wiley Encyclopedia of Food Science and Technology. 2nd ed. England: John Wiley and Sons; 1999.
25. PerkinElmer. 2400 Series II CHNS/O Elemental Analysis. Organic Elemental Analysis. Waltham: PerkinElmer, Inc.; c2013 [cited 2013 Jan 6]; Available from: http://www.perkinelmer.com/Catalog/Product/ID/N2410650.
26. McNeil B, Harvey LM. Practical fermentation technology. England: John Wiley & Sons, Ltd.; 2008
27. Castellanos J, García A, Herrera N, Rodríguez J, Pérez A. Estimación del calor de reacción en el transcurso de bioprocesos. Centro Azúcar. 2002;28(1):37-46.
28. Parikh J, Channiwala SA, Ghosal GK. A Correlation for calculating elemental composition from proximate analysis of biomass materials. Fuel. 2007;86(12-13):1710-9.
29. Cuiping L, Chuangzhi W, Yanyongjie, Haitao H. Chemical elemental characteristics of biomass fuels in China. Biomass Bioenerg. 2004;27(2):119-30.
30. Sánchez JE, Mata G. Hongos comestibles y medicinales en Iberoamérica: investigación y desarrollo en un entorno multicultural. Tapachula: El Colegio de la Frontera Sur; 2012.
31. Vargas-Moreno JM, Callejón-Ferre AJ, Pérez-Alonso J, Velázquez-Martí B. A review of the mathematical models for predicting the heating value of biomass materials. Renew Sust Energ Rev. 2012;16(5):3065-83.
32. Shen J, Zhu S, Liu X, Zhang H, Tan J. The prediction of elemental composition of biomass based on proximate analysis. Energ Convers Manage. 2010;51(5):983-7.
33. Yépez B, Converti A, Maugeri F. Intrinsic activity of inulinase from Kluyveromyces marxianus ATCC 16045 and carbon and nitrogen balances. Food Technol Biotechnol. 2006;44(4):479-83.
34. Andrino A, Morte MA, Honrubia M. Caracterización y cultivo de tres cepas de Pleurotus eryngii (Fries) Quélet sobre sustratos basados en residuos agroalimentarios. An Biol. 2011;(33):53-66.
35. Pineda J, Ramos L, Soto C. Cinética del crecimiento de Pleurotus ostreatus en la etapa de producción del cuerpo fructífero. ICIDCA. 2013;47(3):56-61.
36. Dimian AC, Sorin C. Chemical processing design: Computer-aided case study. Weinheim: Wiley VCH Verlag GmbH & Co. KGaA; 2008.
37. Mitchell D, Krieger N, Berovic M, editors. Solid-state fermentation bioreactors: Fundamentals of design and operation. New York: Springer; 2006.
38. González DM, Echevarría HR, Hernández AP. Termodinámica para ingenieros químicos. La Habana: Editorial Félix Varela; 2006.
Received in November, 2013.
Accepted in January, 2014.
Julio A Pineda-Insuasti. Centro Ecuatoriano de Biotecnología del Ambiente, CEBA. Ibarra, Imbabura, Ecuador. E-mail: pinsuasti@yahoo.com.














