ARTÍCULO ORIGINAL

 

 

Programación entera para modelos lineales

 

Integer programming for linear models

 

 

Daniel Molina Pérez,^I Eric Cabrera Estupiñán^II

^ICentro de Investigaciones Hidráulicas (CIH), Instituto Superior Politécnico José Antonio Echeverría (Cujae). La Habana.
^IIEmpresa de Ingeniería y Proyectos del Petróleo (EIPP). La Habana.

 

 

---

RESUMEN

Se presenta una herramienta para resolver modelos de programación lineal entera, lo que significa encontrar el valor óptimo de la función objetivo para variables de decisión enteras. Es una función llamada nbintprog (non binary integer programming) creada por los autores en el asistente matemático MATLAB (MatrixLaboratory) y para comodidad del usuario presenta una forma similar a las funciones de optimización propias de MATLAB. La existencia de situaciones donde sólo tiene sentido que las variables de decisión, por su naturaleza, sean números enteros y los inconvenientes que presenta la herramienta que propone MATLAB para su solución constituyen los motivos del trabajo. Nbintprog tiene como base matemática una técnica de ramificación y acotación (branch and bound) que junto a estrategias de programación utilizadas presenta características favorables para la solución de dichos modelos.

Palabras clave: MATLAB, nbintprog, optimización, programación entera, programación lineal.

---

ABSTRACT

A new tool able to solve integer linear programming problems is presented. The problem arises when one has to find the optimal value of the objective function for integer decision variables. This tool is a function called nbintprog (non binary integer programming) created by the authors in MATLAB mathematical assistant. To the user's comfort it is presented in a similar way as any other of the typical MATLAB optimization functions. The existence of situations where it only makes sense that the decision variables are integers and the inconvenience of the existing MATLAB function for its solution became the motive of this work. The function is based on the well-known branch and bound technique which together with other programming strategies may eventually reduce the search time of the solution significantly.

Keywords: MATLAB, nbintprog, optimization, integer programming, linear programming.

---

 

 

INTRODUCCIÓN

Un problema de optimización o programación matemática consiste en maximizar o minimizar una función real dado un dominio definido. De forma general, la optimización se basa en el descubrimiento de los «mejores valores» de alguna función objetivo (FO), existiendo una variedad de diferentes tipos de funciones objetivo y diferentes tipos de dominios (Society 2010). Al procedimiento o algoritmo matemático mediante el cual se resuelve un problema formado por una función objetivo lineal y un sistema de ecuaciones o inecuaciones lineales se le llama programación lineal.

Existen casos de modelos lineales en los que por razones físicas se necesita que el valor óptimo de la FO sea resultado de valores enteros para todas las variables de decisión, el algoritmo capaz de resolver este problema se conoce como «programación lineal entera pura» (PLEP). El hecho de conocer las variables de decisión que den solución a un modelo de programación lineal, no significa necesariamente encontrarse cerca de las variables que den solución a la PLEP del modelo. La aproximación al valor entero más cercano de las variables de decisión no siempre conduce a la solución óptima del modelo y en otros casos provoca la violación de algunas de las restricciones (Marrero 1985). Para demostrar lo expresado se presentan los siguientes ejemplos:

Ejemplo (1)

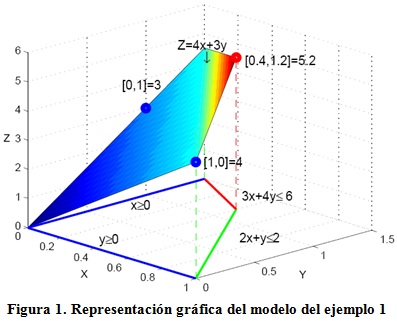
Donde la ecuación (1) es la FO que, en este caso, se busca su máximo valor (ver figura 1).

Las ecuaciones (2), (3), (4) y (5) son las restricciones del dominio, es decir, delimitan lo que se llama el espacio factible, que se ilustra en la figura 1.

Como muestra dicha figura 1 la solución óptima de la PL en este ejemplo es Z(x,y)=5,2 para [x=0,4; y=1,2]. Una aproximación de las variables a sus valores enteros más cercanos sería [x=0; y=1] resultando en Z(x,y)=3. Sin embargo, véase que el punto [x=1; y=0] tiene Z(x,y)=4 lo que prueba que dicha aproximación no garantiza la solución del modelo de PLEP .

Ejemplo (2)

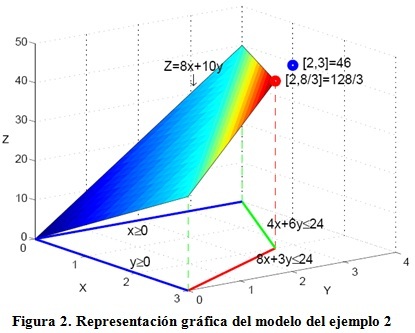
La solución óptima en este ejemplo es Z(x,y)=[128/3] para [x=2; y=8/3]. Una aproximación de las variables a sus valores enteros más cercanos queda [x=2; y=3] la cual se encuentra fuera del dominio del modelo incumpliendo con una de las restricciones, ver figura 2.

Por estas razones para obtener la solución óptima como resultado de variables enteras (PLEP) ha surgido la necesidad de complementar algoritmos utilizados en la PL con estrategias de PLEP. Una de las más eficaces estrategias es el método de ramificación y acotación (branch and bound). Este artículo propone una función programada en MATLAB capaz de resolver modelos de PLEP utilizando dicho método como base matemática.

Dicha herramienta, además de agilizar el proceso manual, extiende sus objetivos a ofrecer notables ventajas sobre otras estrategias como se verá más adelante.

MÉTODO DE RAMIFICACIÓN Y ACOTACIÓN

Se llamará problema relajado (PR) de un problema de PLEP al problema resuelto solamente mediante programación lineal (PL), es decir, sin que existan condiciones de integridad sobre las variables (Wolsey and Nemhauser 1988). El método comienza por la solución del PR del modelo inicial.

La ramificación consiste en dividir cada problema en dos nuevos subproblemas obtenidos mediante la imposición de restricciones excluyentes que dividen el dominio del problema original en dos partes, pero eliminando en ambas partes la solución no entera del problema original (Troncoso 2005), es decir, si xbi es una variable de decisión no entera, entonces se generan dos restricciones xi d» [xbi] (siendo [xbi] la parte entera por defecto de xbi) y xi e» [xbi]+1, que añadidas cada una por separado al problema original, da lugar a dos nuevos subproblemas. En el ejemplo 2, y=8/3=2,67. Por tanto se introducirán las siguientes restricciones: y d» 2; y e» 3, de forma que se ha eliminado una porción del dominio donde no hay soluciones enteras, figura 3.

Una vez que se ramifica se resuelve cada subproblema o nodo, (como se le llamará en lo adelante) mediante PL lineal, es decir, se resuelve el PR de cada uno. Mientras que en ambos nodos exista alguna variable no entera se ramificará el nodo que tenga mejor valor de FO (VFO). El nodo no ramificado pasa a formar parte de una lista de nodos vivos. Una vez encontrado el primer nodo con todas sus variables enteras se tiene el primer VFO de pivote y se confrontará con el VFO de cada nodo vivo. Será ramificado el nodo vivo que tenga mejor VFO que el pivote ya que puede encontrarse una solución entera mejor por dicha rama, de ser así esta se convertiría en el nuevo pivote. Cuando existen varios nodos vivos mejores que el pivote existen los criterios FIFO (first input first output), LIFO (last input first output) y el criterio BIFO (best input first output) donde se ramifica primero el nodo vivo de mejor VFO (Lahoz 2009). Este último criterio será el empleado en la función que se presenta. Por otro lado, el nodo que tenga peor VFO que el pivote se cerrará por acotación y deja de formar parte de la lista de nodos vivos. Garantizando así no explorar todas las soluciones del modelo, fenómeno que puede hacer que la búsqueda de la solución aumente de minutos a años ya que el número de soluciones es grande incluso en pequeños problemas como se muestra:

0 ≤ x ≤ 150 ; 0 ≤ y ≤ 200

posibles soluciones= 151 x 201 =30 351

Ejemplo (3)

Se resuelve el siguiente modelo mediante ramificación y acotación

Donde la solución del PR es Z(x,y)=[7,75] para [x=1; y=3/4], ver figura 4a.

Primera ramificación (figura 4b):

Nodo 1 MAX (Z) = 4x + 5y x ≤ 1 3x + 4y ≤ 6 x ≥ 0 ; y ≥ 0 y ≤ 0

Nodo 2 MAX (Z) = 4x + 5y x ≤ 1 3x + 4y ≤ 6 x ≥ 0 ; y ≥ 0 y ≥ 1

Solución: [x=1; y=0]; Z(x,y)=[4]     Solución: [x=0,67; y=1]; Z(x,y)=[7,67]

En el Nodo1 se encuentra el primer VFO resultante de variables enteras (VFO de pivote), pero no se puede garantizar que sea la solución ya que existe una solución no entera en el nodo 2 con mayor VFO (nodo vivo), lo que hace necesario ramificar dicho nodo.

Segunda ramificación (figura 5a):

Nodo 2-1 MAX (Z) = 4x + 5y x ≤ 1 3x + 4y ≤ 6 x ≥ 0 ; y ≥ 0 y ≥ 1 x ≤ 0

Nodo 2-2 MAX (Z) = 4x + 5y x ≤ 1 3x + 4y ≤ 6 x ≥ 0 ; y ≥ 0 y≥ 1 x ≥ 1

Solución: [x=0; y=1,5]; Z(x,y)=[7,5]        Solución: no factible

El Nodo2-2 carece de variables que puedan satisfacer todas sus restricciones por lo que no tiene solución factible y se cierra, sin embargo el Nodo2-1 tiene un VFO mayor que el VFO de pivote por lo que se tiene que ramificar.

Tercera ramificación (figura 5b):

Nodo 2-1-1 MAX (Z) = 4x + 5y x ≤ 1 3x + 4y ≤ 6 x ≥ 0 ; y ≥ 0 y ≥ 1 ; x ≤ 0 y ≤ 1

Nodo 2-1-2 MAX (Z) = 4x + 5y x ≤ 1 3x + 4y ≤ 6 x ≥ 0 ; y≥ 0 y ≥ 1 ; x ≤ 0 y ≥ 2

Solución: [x=0; y=1]; Z(x,y)=[5]           Solución: no factible

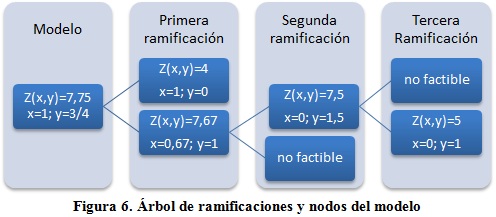
El Nodo 2-1-1 tiene todas sus variables enteras y su VFO es mayor que el VFO de pivote por tanto se convierte en la nueva FO de pivote y al no existir nodos vivos, [x=0; y=1]; Z(x,y)=[5] es la solución óptima del modelo lineal entero. En la figura 6 se muestra el árbol de ramificaciones y nodos.

NBINTPROG

La función propuesta atiende al nombre de nbintprog y para su llamada debe encontrarse su ruta como carpeta actual (Current Folder) de MATLAB. En esta sección se describe el modo de trabajo de la herramienta.

Declarando vectores y matrices

La función nbintprog resuelve problemas de programación lineal entera del tipo:

MIN Z = f x x     

Sujeto a:

A x x ≤ b

Aeq x x = beq

lb≤ x ≤ ub

Donde:

ƒ: Vector de coeficientes que multiplican a las variables de decisión en la FO

x: Vector de variables de decisión (solución)

b: Vector de términos de la derecha de las restricciones de desigualdad

beq: Vector de términos de la derecha de las restricciones de igualdad

lb: Vector que define la frontera inferior del dominio

ub: Vector que define la frontera superior del dominio

A: Matriz de coeficientes que multiplican a las variables en las restricciones de desigualdad

Aeq: Matriz de coeficientes que multiplican a las variables en las restricciones de igualdad

Es importante el hecho de que nbintprog al igual que las funciones propias de MATLAB solo minimizan la FO, por tanto si se quiere maximizar se debe multiplicar por (-1) toda la FO como se muestra en la figura 7. De igual forma todas las restricciones de desigualdad las considera como (d»), por tanto las que sean (e») se deben multiplicar por (-1) para cambiar el sentido de la desigualdad, tal transformación se realiza en las ecuaciones (13) y (14) del ejemplo 3 resultando como se muestran en la figura 7.

Anteriormente se declararon las matrices y vectores que necesita nbintprog, ahora se procede a hacer un llamado a la función y la forma es como se muestra en la ecuación (15):

Los inputs o datos de entrada que se encuentran a la derecha separados por coma son los datos que necesita el programa, los cuales se declararon anteriormente, un aspecto muy importante es que el orden de los inputs debe ser el específico de cada función. Se puede prescindir de algunos inputs, su utilización depende de los tipos de restricciones que existan en el modelo. Sin embargo si no se necesita un input intermedio, en su posición se debe declara una matriz nula para no alterar el orden de los demás, ver figura 8.

[…] = nbintprog (f, A, b) resuelve el modelo sujeto a A x x ≤ b

[…] = nbintprog (f, A, b, Aeq, beq) resuelve el problema de arriba satisfaciendo además las restricciones de igualdad del tipo Aeq x x = beq

[…] = nbintprog (f, A, b, Aeq, beq, lb, ub) define además, la frontera inferior y superior de todas las variables de decisión, de modo que la solución siempre queda en el rango lb ≤ x ≤ ub

[…] = nbintprog (f, A, b, Aeq, beq, lb, ub, x0) se define además, un punto inicial de búsqueda

[…] = nbintprog (f, A, b, Aeq, beq, lb, ub, x0, options_int) options_int es una estructura de datos que permite entrar al programa diferentes parámetros para la búsqueda de la solución; a continuación se muestra cuáles son dichos parámetros y posteriormente cómo declararlos:

· Tolerancia con la cual las variables de decisión son consideradas enteras (TolXInteger):

Esta tolerancia es necesaria debido a que MATLAB guarda cada número con una precisión de 16 lugares decimales, por lo que buscar una combinación de variables realmente enteras elevaría el número de ramificaciones y de tiempo, buscando una precisión innecesaria. Nbintprog al igual que las funciones propias de MATLAB tiene una TolXInteger por defecto de 10^-8.

· Tolerancia de parada de la FO (TolFun):

En resumen, TolFun tiene en cuenta la proximidad del VFO de pivote con el mejor VFO de los nodos vivos, de forma que cuando esta proximidad es muy pequeña el programa se detiene y ofrece como solución la FO de pivote actual. Esta herramienta puede ser muy útil ya que existen problemas que presentan muchos nodos vivos extremadamente cercanos al VFO de pivote, y una vez que se ramifican resultan valores peores que dicho pivote lo que trae implícito un consumo de tiempo innecesario. El hecho de utilizar la estrategia de selección BIFO hace que en cada iteración disminuya esta tolerancia. Nbintprog al igual que las funciones propias de MATLAB tiene una TolFun por defecto de 10^-3.

· Máximo número de iteraciones(MaxIter)

Para no exceder un determinado número de iteraciones. La solución que devuelve es la correspondiente al pivote actual, tiene por defecto un valor de 1000 iteraciones.

· Máximo número de ramificaciones (MaxNodes)

Para no exceder un determinado número de nodos ramificados. La solución que devuelve es la correspondiente al pivote actual, tiene por defecto un valor de 5000 ramificaciones.

· Opción de visualización de los resultados del proceso iterativo de nbintprog (Display)

Para observar los resultados de cada iteración es necesario llevar el parámetro Display de su estado apagado (por defecto) a estado (iter) posteriormente se muestra la manera de hacerlo.

[…] = nbintprog (f, A, b, Aeq, beq, lb, ub, x0, options_int, options) options son una serie de opciones aplicables sólo a la función linprog que constituye una herramienta de apoyo para nbintprog, útil para la solución del PR, podría darse el caso especial en que se necesite la modificación de esta herramienta y options es la vía, para más información sobre options buscar en la ayuda de MATLAB la función linprog.

Para modificar los valores de los parámetros por defecto de options_int u options se utiliza la función optimset como se muestra en la ecuación (18). Es muy importante que los parámetros se escriban como aquí se indica incluyendo sus mayúsculas, ver su aplicación en el ejemplo 4.

Los datos de salida (outputs), donde MATLAB devolverá los resultados obtenidos, se declaran entre corchetes en la parte izquierda de la función separados por coma, teniendo en cuenta la importancia del orden, como se observa a continuación:

x = nbintprog (…) devuelve las variables de decisión que dieron solución al problema

[ x, Fo] = nbintprog (…) devuelve además, el valor de la FO de la solución

[ x, Fo, exit ] = nbintprog (…) devuelve además, la razón de parada del programa

exit = 1: El programa convergió a la solución

exit = 2: La TolFun existente fue menor que la TolFun admisible

exit = 3: El número de iteraciones sobrepasó a MaxIter

exit = 4: El número de ramificaciones sobrepasó a MaxNodes

[ x, Fo, exit, output ] = nbintprog (…) output es una estructura de datos que devuelve el tiempo empleado en encontrar la solución y la cantidad de iteraciones realizadas

Ejemplo (4)

Plantear y resolver el modelo del ejemplo 3 mediante nbintprog con una TolFun=0, pues se desea ramificar todos los nodos vivos con mejor VFO que el pivote, por muy cerca que se encuentren de este, una TolXInteger = 0,00001 y también se quiere visualizar la tabla de resultados, declarar las ecuaciones (13) y (14) como frontera inferior.

En la tabla 1 se observan los resultados de cada iteración. En la iteración 2 aparece un asterisco en la izquierda de la tabla, esto ocurre cada vez que hay un cambio de FO de pivote. Posteriormente nbintprog muestra la solución, véase que x es un vector que contiene a los valores de [x ; y]

PROBLEMA DE PRODUCCIÓN DE ASPERSORES

Un taller de montaje de aspersores consta de tres secciones A, B y C. En cada sección se pueden ensamblar tres tipos diferentes de aspersores A-10, A-12 y A-15. La capacidad de producción de cada sección varía dependiendo del tipo de aspersor a ensamblar como indica la tabla 2. Acorde con una orientación, se necesita que por cada aspersor A-10, se fabrique un aspersor A-12 y dos A-15. Determinar y resolver el modelo matemático que maximice el número de aspersores a fabricar.

Formulación estándar del modelo

Variables de decisión:

XA_A-10 = Cantidad de aspersores A-10 a producir por día en la sección A.

XA_A-12 = Cantidad de aspersores A-12 a producir por día en la sección A.

XA_A-15 = Cantidad de aspersores A-15 a producir por día en la sección A.

XB_A-10 = Cantidad de aspersores A-10 a producir por día en la sección B.

XB_A-12 = Cantidad de aspersores A-12 a producir por día en la sección B.

XB_A-15 = Cantidad de aspersores A-15 a producir por día en la sección B.

XC_A-10 = Cantidad de aspersores A-10 a producir por día en la sección C.

XC_A-12 = Cantidad de aspersores A-12 a producir por día en la sección C.

XC_A-15 = Cantidad de aspersores A-15 a producir por día en la sección C.

Función objetivo:

-Restricciones de capacidad de producción

-Otras restricciones adicionales.

-Restricciones de no negatividad:

Adecuación del modelo para bintprog

A continuación se resuelve el problema utilizando una función propia de MATLAB llamada bintprog. Dicha función está concebida para resolver modelos de programación lineal entera binaria. De modo que las variables de decisión solo pueden tomar valores cero-uno (0-1), útil para problemas de grafos y redes (Cabrera 2012). Dicha función puede resolver modelos de PLEP aplicando un artificio matemático (MathWorks 2012). La idea fundamental es representar cada variable de decisión (X) como un conjunto de variables binarias (z₁,z₂,...z_n) , el cual tiene la forma:

Por ejemplo la variable XA_A-10 tiene una capacidad de producción diaria de hasta 85 aspersores y se representa con el conjunto mostrado en la ecuación (27). Esta forma permite que la variable XA_A-10 pueda tomar todos los valores enteros desde 0 hasta 127, rango que encierra los posibles valores que puede alcanzar dicha variable.

Aplicación a cada variable de decisión:

Función objetivo binaria:

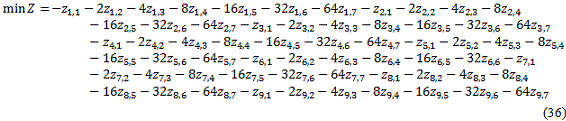
-Restricciones de capacidad de producción.

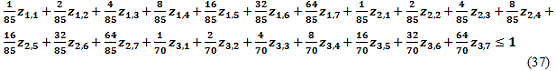
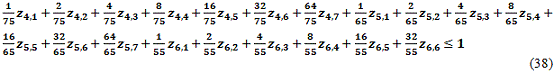
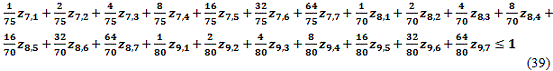
-Otras restricciones adicionales.

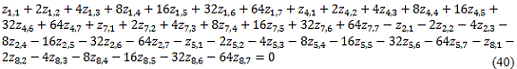
-Restricciones de no negatividad:

Declaración del modelo en MATLAB para bintprog

Se presenta en la tabla 3.

Solución mediante bintprog

XC_A-10 = 0

XC_A-12 = 0

XC_A-15 = 80

XB_A-10 = 57

XB_A-12 = 6

XB_A-15 = 6

XA_A-10 = 0

XA_A-12 = 51

XA_A-15 = 28

Valor de la función objetivo (fval)=228

Razón de parada (exit)=se excedió el número de ramificaciones por defecto de bintprog

Declaración del modelo en MATLAB para nbintprog

Se presenta en la tabla 4.

Solución mediante nbintprog

XA_A-10 = 2

XA_A-12 = 52

XA_A-15 = 25

XC_A-10 = 0

XC_A-12 = 2

XC_A-15 = 77

XB_A-10 = 55

XB_A-12 = 3

XB_A-15 = 12

Valor de la función objetivo (fval)=228

Razón de parada (exit)=convergencia a la solución

Comparación de los resultados

Como se observa bintprog se detiene producto que excede el número de ramificaciones por defecto aproximadamente a los 28 minutos como muestra la tabla 5; aquí cabe la posibilidad de modificar el valor de MaxNodes, pero no es el objetivo. Pese a que el programa se detiene, ofrece la mejor solución que presenta hasta el momento, con el inconveniente que dicha solución posee una TolFun=0,78%. Esta tolerancia significa que, a los 28 minutos de cómputo, existen nodos vivos y por tanto la posibilidad de encontrar mejores soluciones que la mostrada. Como se muestra en la tabla 5, cuando bintprog se detiene aún presenta 23165 nodos vivos. Esta significativa desaceleración de la convergencia a la solución se debe al aumento del número de variables.

¿Por qué el incremento de variables desacelera significativamente la convergencia a la solución?

En la primera ramificación del ejemplo 3, el nodo 2 tiene la solución [x=0,67; y=1], sin embargo al ramificarlo, el Nodo 2-1 tiene como variables [x=0; y=1,5], véase que al hacer entera (x), la variable (y) que era entera producto de la primera ramificación del modelo vuelve a tomar un valor fraccionario. Por tanto, una variable entera dentro de la solución puede dejar de serlo ante la ramificación de otras, por lo que el programa va restringiendo el dominio de cada variable fraccionaria hasta que encuentre una combinación de variables enteras o se cierre el dominio y no se encuentre solución, entonces salta a otro nodo vivo. Si el número de variables es grande, mientras se hace entera una, son más las que pueden dejar de serlo. De modo que para que bintprog logre que las 62 variables binarias sean enteras tiene que realizar muchas ramificaciones. Por dicha razón bintprog no encuentra su primera solución hasta la ramificación 12789. Además, un incremento de ramificaciones significa generar mayor cantidad de nodos vivos que posteriormente puede ser obligatorio ramificar. De modo que cuando bintprog encontró su primera solución ya contaba con 6596 nodos vivos, esto se puede corroborar en la tabla de resultados iterativos de bintprog cuando se corre el modelo. Por esta razón el hecho de que la cantidad de variables binarias de bintprog dependa de la capacidad máxima de las variables no binarias puede resultar insatisfactorio.

Nbintprog no se encuentra sometido a dicho fenómeno por lo que converge más rápido a la solución. En el caso del modelo de aspersores no solo converge a la solución 14 veces más rápido que bintprog (tabla 5), sino que el resultado presenta una calidad superior (TolFun=0), lo que significa que se ramificaron todos los nodos vivos y no se encontró mejor solución entera. Para hacer una comparación con soluciones de igual calidad se puede decir que nbintprog alcanza una TolFun ligeramente menor que 0,78% en la iteración número 23 para un tiempo de un minuto y medio, queda por parte del lector comprobarlo.

 

CONCLUSIONES

Se presenta la función nbintprog para MATLAB, capaz de resolver modelos de programación lineal entera pura (PLEP) utilizando como base matemática el método de ramificación y acotación (branch and bound) empleando la estrategia BIFO (best input first output). Dicha herramienta, a diferencia de la función bintprog (intrínseca de MATLAB), no requiere de una adecuación de su formulación estándar a un modelo binario para resolver problemas no binarios de programación lineal entera.

Se realiza una comparación integral basada en el empleo de bintprog y nbintprog para resolver un problema de ingeniería. De esta comparación se puede concluir que se evidencian los inconvenientes que trae consigo el hecho de que la cantidad de variables binarias que se requieren para la adecuación de un modelo no binario dependa de la capacidad máxima de las variables no binarias. Esto hace que la solución brindada por la función bintprog tarde 14 veces más que la brindada por nbintprog. Además con la solución de nbintprog se ramifican todos los nodos vivos y no se encuentra mejor solución entera, mientras que bintprog brinda un resultado cuando excede el número máximo prefijado de ramificaciones por defecto.

 

REFERENCIAS

Cabrera E. «Programación lineal.», Conferencia de planeamiento y operación de los recursos hidráulicos, CIH, Facultad de Ingeniería Civil, Cujae, La Habana, 2012.

Lahoz P. «Programación lineal entera», Investigacion operativa, extraído de: http://ocw.unizar. es/modelos-de-investigacion-operativa/OCWProgEntera.pdf, en enero 2013 2009.

Troncoso A. «Técnicas avanzadas de predicción y optimización aplicadas a sistemas de potencia», Tesis de doctorado, Dpto. de lenguajes y sistemas, Univ. de Sevilla, España, 2005.

Marrero N. «Técnicas de optimización aplicadas a la ingeniería hidráulica», Ed. ISPJAE, Facultad de Ingeniería Civil, ISPJAE, La Habana,1985.

MathWorks «Solve binary integer programming problems», Optimization Toolbox For Use with MATLAB®, MATLAB, USA, 2012.

Society I. C. «The Nature of Mathematical Programming». Mathematical Programming Glossary extraído de: http://www.glossary.computing.society.informs.org en enero 2013, 2010.

Wolsey L. and Nemhauser G. «Integer and Combinatorial Optimization.», Ed. John Wiley& Sons, New York, 1998.

 

 

Recibido: 11 de octubre de 2013.
Aprobado: 15 de octubre de 2013.

 

 

Daniel Molina Pérez, Eric Cabrera Estupiñán, Centro de Investigaciones Hidráulicas (CIH), Instituto Superior Politécnico José Antonio Echeverría (Cujae). La Habana, Empresa de Ingeniería y Proyectos del Petróleo (EIPP). La Habana. e-mail: [e-mail], e-mail: [e-mail]