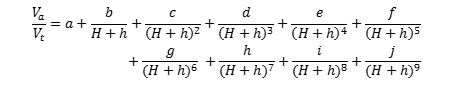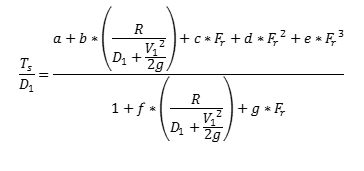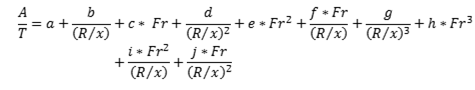INTRODUCCIÓN
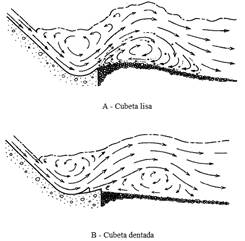
Las cubetas sumergidas han sido objetos de estudio durante muchos años y en general hay coincidencia entre los investigadores del tema que son dos los tipos de mejores resultados: las cubetas lisas y las dentadas, de las cuales se muestran dos ejemplos en la figura 1 (Pardo 2017).
FUNCIONAMIENTO DE LAS CUBETAS LISAS Y DENTADAS
Las cubetas lisa y dentada son mostradas en funcionamiento en la figura 2. El comportamiento hidráulico y la configuración resultante de las dos cubetas son significativamente diferentes. Ambos tipos requieren mayor tirante aguas abajo que el salto hidráulico. En la cubeta lisa todo el flujo es lanzado hacia arriba por el fondo de la cubeta para crear un borbotón de agua en la superficie y un fuerte remolino sumergido sobre el fondo del río. La severidad del borbotón alto y del remolino sumergido depende de la profundidad del agua a la salida TA, de manera que bajos TA producen los más violentos borbotones y remolinos (Peterka 1984).
La corriente superior del remolino mueve material del fondo desde aguas abajo y lo deposita dentro de la cubeta; desde aquí es lanzado hacia abajo y vuelto a lanzar hacia la cubeta. Este constante movimiento de sedimentos contra el hormigón lo va abrasando y además genera operación asimétrica del aliviadero, lo cual no es conveniente.
En el caso de la cubeta dentada parte del flujo pasa entre los dientes y se abre lateralmente y otra parte sobre los dientes es lanzada lejos desde la solera, por tanto, el flujo es dispersado y distribuido sobre una gran área dando una concentración de flujo con menos poder erosivo que el de la cubeta lisa.
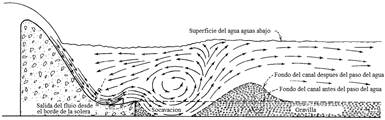
Por otro lado, no se produce introducción de gran cantidad de material del terreno en la cubeta y las pequeñas cantidades que lo hacen, son rápidamente barridas hacia aguas abajo. Con la cubeta dentada, el barrido total tiene lugar para TA ligeramente superiores a los de la cubeta lisa y si el TA es muy alto, el flujo puede sumergirse desde la solera y erosionar el fondo del canal, como se muestra en la figura 3; en la cubeta lisa tal sumersión del flujo no se produce.
En general, no obstante lo anterior, la cubeta dentada da resultados superiores a la lisa, particularmente para valores bajos de TA.
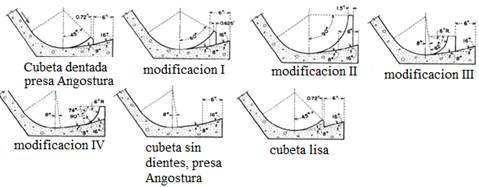
En la figura 4 se muestran algunas de las modificaciones que se han hecho a la cubeta dentada para realizar estudios en modelos físicos.
Procedimiento de diseño propuesto por Peterka:
La cubeta dentada puede ser usada como disipador de energía en la base de un vertedor. Los estudios realizados muestran que la cubeta dentada es superior a la lisa en todos los aspectos. Siempre que las condiciones prácticas lo permitan, debe ser usado el diente mayor recomendado en la modificación de diseño II de la figura 4.
Una versión sencilla de los siete pasos requeridos para el diseño de una cubeta es:
1. Determinar Q, q (gasto específico en la cubeta), V 1 , D 1 ; calcular el número de Froude para el gasto máximo y para caudales intermedios según F=V 1 /(g D 1 )0,5 . Específicamente para determinar la velocidad de entrada a la cubeta se puede emplear la figura 5.
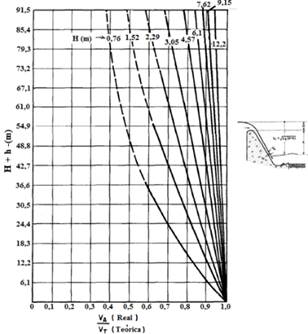
Figura 5 Curvas para la determinación de la velocidad de entrada a la cubeta para pendientes 0,8: 1 a 0,6:1 [Fuente: Peterka (1984)]
Se puede utilizar la ecuación (1) y los parámetros de las tablas 1 y 2 como una alternativa a la figura 5.
Tabla 1 Parámetros de la ecuación (1)
| Parámetros | Curva 0,76 | Curva 1,52 | Curva 2,29 | Curva 3,05 |
|---|---|---|---|---|
| a | 0,999314881 | 0,999807009 | 0,998588447 | 0,999162211 |
| b | -0,01770409 | -0,00797307 | -0,00375518 | 0,000131434 |
| c | 0,000850479 | -7,4469E-05 | -0,0003099 | -0,00114495 |
| d | -7,6298E-05 | 1,97758E-05 | 3,14323E-05 | 0,000140923 |
| e | 3,99122E-06 | -1,4636E-06 | -1,7051E-06 | -8,4836E-06 |
| f | -1,1860E-07 | 5,45455E-08 | 5,32068E-08 | 2,80628E-07 |
| g | 2,08175E-09 | -1,1346E-09 | -9,8188E-10 | -5,3656E-09 |
| h | -2,1399E-11 | 1,33483E-11 | 1,05924E-11 | 5,90874E-11 |
| i | 1,1918E-13 | -8,2961E-14 | -6,1749E-14 | -3,4779E-13 |
| j | -2,7778E-16 | 2,11666E-16 | 1,50222E-16 | 8,47251E-16 |
Tabla 2 Parámetros de la ecuación (1)
| Parámetros | Curva 4,57 | Curva 6,1 | Curva 7,62 | Curva 9,15 | Curva 12,2 |
|---|---|---|---|---|---|
| a | 1,000459366 | 1,000218708 | 0,999451008 | 0,999330523 | 0,999814716 |
| b | -0,00552328 | -0,00229194 | 0,002445552 | 0,001134019 | -0,00079455 |
| c | 0,000694959 | 0,000191014 | -0,00103896 | -0,00038157 | 0,000253677 |
| d | -6,7104E-05 | -2,1060E-05 | 0,000110414 | 3,68964E-05 | -3,3538E-05 |
| e | 3,45383E-06 | 1,19565E-06 | -6,0082E-06 | -1,7443E-06 | 1,90112E-06 |
| f | -1,0322E-07 | -3,9901E-08 | 1,86743E-07 | 4,31289E-08 | -5,8431E-08 |
| g | 1,85014E-09 | 8,04239E-10 | -3,4406E-09 | -5,7197E-10 | 1,04883E-09 |
| h | -1,9605E-11 | -9,5439E-12 | 3,70893E-11 | 3,81305E-12 | -1,1015E-11 |
| i | 1,1311E-13 | 6,10053E-14 | -2,1582E-13 | -9,4023E-15 | 6,28352E-14 |
| j | -2,7355E-16 | -1,6134E-16 | 5,23029E-16 | -5,5822E-18 | -1,5049E-16 |
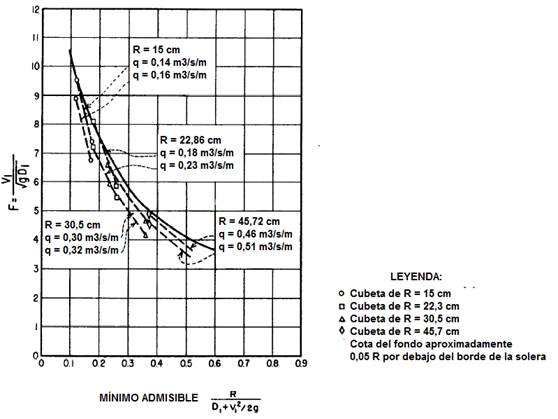
2. Entrar en la figura 6 con F r1 para encontrar el parámetro radio de la cubeta R/(D 1 + V1 2/2g) a partir del cual se calcula el radio mínimo permisible R de la cubeta.
3. Entrar en la figura 7 con R/(D
1
+ V1
2/2g) y F
r1
para obtener
Se puede utilizar la ecuación (2) y los parámetros de la tabla 2 como alternativa a la figura 7.
Tabla 2 Parámetros de la ecuación (2)
| a | -0,02782338 |
| b | -0,429494774 |
| c | 1,408516631 |
| d | -0,109691939 |
| e | -0,257728896 |
| f | 0,119760698 |
| g | -0,076936322 |
4. Entrar en la figura 8 para de forma similar al paso 3 obtener T máx .
Se puede utilizar la ecuación (3) y los parámetros de la tabla 3 como una alternativa a la figura 8 para los valores de R/(D 1 + V1 2/2g) <0,4.
Tabla 3 Parámetros de la ecuación (3)
| a | 4,671576839 |
| b | -29,14256478 |
| c | 44,98066395 |
| d | 0,300040151 |
| e | -0,016622226 |
| f | 0,005467051 |
| g | -4,021594796 |
| h | 6,707543555 |
| i | -3,350653296 |
| j | -0,024159164 |
5. Establecer la cota del fondo de la cubeta de manera tal que las curvas de elevaciones de TA estén dentro de los límites T mín y T máx . Colocar el extremo final de la cubeta así como su fondo, por encima del fondo del cauce de salida. Para un mejor comportamiento, colocar la cubeta de manera que TA esté cercano a T mín . Verificar la ubicación y determinar el factor de seguridad contra el barrido total a partir de la figura 9 siguiendo el mismo procedimiento que el paso 3.
Se puede utilizar la ecuación (4) y los parámetros de la tabla 4 como una alternativa a la figura 9.
6. Completar el diseño de la cubeta, usando la figura 1, para obtener forma, dimensiones y espaciamiento de los dientes, etc.
7. Usar las figuras 10 y 11 para estimar los perfiles de la superficie del agua dentro y aguas abajo de la cubeta.
Tabla 4 Parámetros de la ecuación (4)
| a | 0,026486158 |
| b | 0,206769989 |
| c | 1,183170646 |
| d | -0,089062212 |
| e | -0,000898493 |
| f | -0,166936533 |
| g | -0,081472753 |
Se puede utilizar la ecuación (5) y los parámetros de la tabla 5 como alternativa a la figura 11.
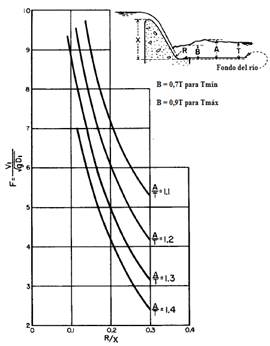
Figura 11 Características del perfil de la superficie del agua para cubetas dentadas [Fuente: Peterka (1984)]
Tabla 5 Parámetros de la ecuación (5)
| a | 1,197107692 |
| b | 0,180794619 |
| c | -0,123454194 |
| d | 0,013249777 |
| e | 0,022159393 |
| f | -0,045475544 |
| g | 0,000453837 |
| h | -0,003638423 |
| i | 0,008449392 |
| j | -0,004736857 |
CONCLUSIONES
Las características de las cubetas tanto lisas como dentadas son bien conocidas, lo cual permite su empleo como disipador de energía en obras hidráulicas.
Las principales herramientas para el diseño hidráulico de las cubetas que se han recopilado a partir de la literatura especializada, han sido procesadas para presentar ecuaciones polinómicas que facilitan el empleo de las mismas mediante sistemas informáticos.