INTRODUCCIÓN
Hart et al. (1979) según cita Díaz (2001), demostraron que las eficiencias de almacenamiento, aplicación, distribución y uniformidad absoluta de la distribución, son las requeridas para describir adecuadamente la calidad del desempeño hidráulico de los sistemas de riego superficial. Por su parte, Kanya (2007) calificó como un desafío la determinación del comportamiento de la infiltración del agua en el riego por surcos, debido a la variabilidad en espacio y tiempo de las propiedades hidrofísicas del suelo, así como las posibilidades de variación de los tiempos de oportunidad.
Pérez y Jiménez (2018), utilizaron diferentes modelos empíricos para describir el comportamiento de la infiltración mediante evaluaciones de campo en suelos ferralíticos, corroborándose los resultados de la experiencia nacional e internacional en cuanto a que el modelo de Kostiakov - Lewis continúa siendo el más confiable, requiriéndose para la determinación de los parámetros K y a, según Elliot et al. (1983), de la aplicación del método de dos puntos de aproximación en la fase de avance. Además, se destaca la aplicación de un importante condicionante de manejo del agua para la fase de mojado, reduciéndose el tiempo de infiltración en la cola de los surcos.
Shepard et al. (1993) propusieron el método de un punto de aproximación para predecir los parámetros de infiltración (A1 y S1) requeridos en el modelo de Philip y precisados a partir del tiempo de la fase de avance. Sin embargo, Bautista and Walker (2010), declararon la dificultad real del método citado, llegándose a la conclusión de que el mismo introduce serios errores en los resultados, agravándose aún más, para tiempos largos de riego. Este hecho fue examinado y aprobado por el Comité de Riego, Drenaje y Medioambiente, así como, por el Instituto de Recursos Hídricos de ASABE (American Society of Agricultural and Biological Engineers).
Por último, Pereira et al. (2010) afirmaron que la sostenibilidad ambiental de los sistemas de riego por surcos, exige de un diseño, manejo y operación del riego, con caudales de aplicación apropiados, que minimicen las perdidas por conceptos de erosión y arrastre de agroquímicos (NPK) fuera de la zona de las raíces de los cultivos.
El objetivo propuesto consistió en: evaluar 5 modelos empíricos de infiltración para tres caudales de riego, mediante pruebas de campo y análisis de calidad del desempeño del riego en suelos oscuros plásticos.
MATERIALES Y METODOS: DATOS DE CAMPO
Los datos asociados al riego por surcos con flujo de agua continuo, se tomaron a partir de los resultados de evaluaciones de campo con fines de riego, en suelos oscuros plásticos de un bloque ingeniero cañero, irrigado con sifones plásticos flexibles en condiciones de investigación - producción, según reportes de Pérez et al. (1989). Para cada una de las evaluaciones del caudal, se habilitaron tres surcos de riego con espaciamientos de 1,6 m, y estaquillado en el surco central cada 20 m, para favorecer la toma de lecturas de avance y recesión del agua. Además, se utilizaron dispositivos hidrométricos Parshall y aforadores portátiles para la determinación del caudal de entrega de agua a los surcos, así como sifones plásticos de PVC, diseñados y construidos para esta técnica de regadío. Los caudales evaluados fueron: Qo = 3,2 L/s, Qo = 4,4 L/s y Qo = 5,0 L/s.
A diferencia de las evaluaciones precedentes en dichos suelos, realizadas mediante la aplicación de un solo modelo empírico de infiltración, en el presente trabajo se procedió, para cada caudal, a las respectivas determinaciones de las láminas de agua infiltradas mediante cada una de las ecuaciones empíricas de los cinco modelos evaluados. Sobre esta base, fueron determinadas las magnitudes de las láminas de agua infiltradas (Zi) en el perfil del suelo, en los puntos: cabecera, ¼ L, ½ L, – L, y L (cola del surco). Ello en función de los respectivos tiempos de oportunidad del agua en los puntos referidos del surco central, lo cual propició:
La correcta representación de los tipos de comportamiento de las láminas de agua infiltradas para cada uno de los modelos, de forma gráfica por caudal evaluado [Laminas infiltradas vs longitud del surco y Laminas infiltradas vs tiempo de oportunidad].
La determinación de las magnitudes de los indicadores de calidad y desempeño del riego (eficiencias), para cada uno de los cinco modelos por caudal evaluado. En resumen, resultaron necesarias no menos de 15 evaluaciones con cada uno de los tres programas de computación utilizados.
NORMATIVAS VIGENTES
Todo lo anteriormente expuesto se adaptó a las normativas científico - técnicas vigentes y en particular, a la Norma Ramal del Ministerio de la Agricultura NRAG (2016), ajustándose a esta, el proceso de cálculo para el diseño y evaluación de cada caudal mediante numerosas programaciones en Excel: DIERIS (Diseño y Evaluación del Riego por Surcos), el cual contiene una condicionante de manejo del agua en función del tipo de suelo (Ferralíticos Rojos y Oscuros Plásticos). En este sentido, para favorecer el ahorro del recurso agua durante la fase de mojado (satisfacción limitada de Zr [dosis neta parcial de riego] aguas abajo), se estableció que el tiempo de mojado (Tm) fuese el 56 % del tiempo de infiltración (Ti) de la lámina de agua requerida.
Además, se utilizaron los softwares SIRMOD II y SIRMUD III, reconocidos por el Comité de Riego Drenaje y Medioambiente de la ASABE como estándares para la evaluación, diseño y operación de la técnica de riego de referencia. Básicamente, las determinaciones de las magnitudes de los caudales (L/s): Qmne (máximo no erosionable) y Q (mínimo), confirmaron la adecuada selección de los caudales (Qo) utilizados. En todos los casos se corroboraron las magnitudes de la velocidad del agua próxima a la cabecera del surco, resultando inferiores que la velocidad máxima admisible para dichos suelos.
MODELOS, ECUACIONES EMPIRICAS, DATOS DE CAMPO Y EFICIENCIAS
Respecto a la infiltración del agua en el riego por surcos, se ratifica su importancia en cuanto a la reposición del almacenamiento de este recurso en la zona de las raíces de los cultivos, lo cual asegura el rendimiento óptimo de las plantaciones. En la tabla 1 se muestran los modelos evaluados y a continuación sus respectivas ecuaciones empíricas para la determinación de las láminas de agua infiltradas en el perfil del suelo; mientras que en las tablas 2 y 3, se muestran importantes datos de campo, así como las formulaciones recomendadas para la determinación de las eficiencias que caracterizan a los eventos de riego analizados.
Tabla 1 Modelos evaluados (Pérez y Jiménez 2018)
| No. del modelo | Denominación del Modelo |
|---|---|
| 1 | Modelo de Kostiakov - Lewis. |
| 2 | Modelo de Philip. |
| 3 | Modelo del Soil Conservation Service (SCS) de 1992. |
| 4 | Modelo de Kostiakov - Lewis, que incluye el efecto de la relación entre el perímetro mojado medio ( |
| 5 | Modelo de Kostiakov - Lewis, incluye el efecto de la relación entre el perímetro mojado en un punto ( |
Ecuaciones empíricas para cada modelo (Pérez y Jiménez 2018)
donde: Zi: lámina infiltrada (m3/m), siendo K: coeficiente de Kostiakov (m3/m/min) y t: tiempo de oportunidad (min), a: exponente de Kostiakov, fo: velocidad de infiltración estabilizada (m3/m/min). Estos coeficientes se obtienen mediante el método de balance del volumen de agua con dos puntos de aproximación en evaluaciones de campo, método de Elliot et al. (1983).
donde: Zi: lámina infiltrada (m3/m), t: tiempo de oportunidad (min), A 1 : parámetro gravitacional (m2/min = m3/m/min) y S 1 : Sorbilidad (m3/m/min).
donde: Zi: expresada en (m3/m) y t: tiempo de oportunidad (min).
Los coeficientes K, a, y fo, se obtuvieron a partir de valores estimados en una tabla del Soil Conservation Service (SCS) de 1992. En esa tabla se toma como referencia el tipo de suelo y, acorde con este, se seleccionan los valores estimados o tentativos para los coeficientes empíricos (Kostiakov - Lewis).
donde: Zi: expresado en (m3/m), t = tiempo de oportunidad en (min). C: coeficiente en función del tipo suelo. También contiene la relación entre el perímetro mojado medio (PM) y el espaciamiento entre surcos (Esp).
donde: Zi: se expresa en (m3/m), la ecuación contiene la relación entre Pi: perímetro mojado en un punto de L y Pm: el perímetro húmedo promedio y φ es función del exponente de Kostiakov y del coeficiente que depende de la geometría del surco.
Tabla 2 Datos de campo
| AREA DEL BLOQUE: | BLOQUE # 0 68 ( |
||
|---|---|---|---|
| DATOS: | Evaluación 1 | Evaluación 2 | Evaluación 3 |
|
|
3,2 | 4,4 | 5,0 |
|
|
0,001 | 0,001 | 0,001 |
|
|
1,6 | 1,6 | 1,6 |
|
|
245 | 250 | 380 |
|
|
0,0031 | 0,0182 | 0,0072 |
| 0,651 | 0,293 | 0,52 | |
|
|
0,00011 | 0,00013 | 0,00015 |
|
|
30 | 35 | 40 |
|
|
59 | 63 | 108 |
|
|
97 | 89 | 145 |
|
|
38 | 26 | 36 |
|
|
6,73 - 1,38 | 6,74 - 1,22 | 7,3 - 1,52 |
Qo: Caudal, So: pendiente, Esp: espaciamiento, Ls: longitud del surco, K y n: coeficientes de Kostiakov, fo: velocidad de infiltración estabilizada, Zreq: dosis de riego, Tav: tiempo de avance del agua, Tcorte: tiempo de corte o aplicación, Tm: tiempo de la fase de mojado (56 % del tiempo de infiltración de Zreq). Qmne: caudal máximo no erosionable, Qmin: caudal mínimo admisible.
RESULTADOS Y DISCUSION: LAMINAS DE AGUA INFILTRADAS, EFICIENCIAS Y ESTADÍGRAFOS
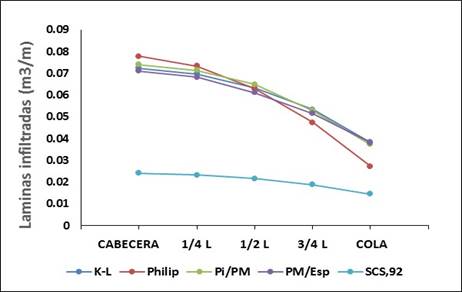
Respecto al primer caudal evaluado (Qo = 3,2 L/s, Ls = 245 m y Zr = 30 mm), se constató que los mejores comportamientos de las magnitudes de las láminas de agua infiltradas (Z i ) en toda la longitud de los surcos, se asociaron con los modelos 1, 4 y 5, tabla 1, citados en el capítulo anterior, los cuales aparecen bastante solapados (figura 1), hecho que se corresponde con Kanya (2007). Dichos modelos están asociados con los mejores resultados de las eficiencias de almacenamiento, aplicación, distribución y uniformidad absoluta de la distribución del agua en los surcos, tabla 4, lo cual se corresponde con los resultados reportados por Pérez et al. (1989) en dichos suelos.
Tabla 3 Cálculo de las eficiencias del riego por surcos
| EFICIENCIAS DEL RIEGO POR SURCOS: FORMULACIONES |
|---|
| Eficiencia de Almacenamiento (%) |
| Eficiencia de Aplicación (%) |
| Eficiencia de Distribución (%) |
| Uniformidad Absoluta de Distribución (%) |
En la figura 1 se revela el comportamiento de las láminas de agua infiltradas para los modelos evaluados en diferentes puntos de la longitud de los surcos (cabecera, ¼ L, ½ L, – L y extremo aguas abajo). Apreciándose que el comportamiento del modelo 2 (Philip), se presentó incoherente, ya que a partir de la mitad de la longitud del surco (190 m), los valores de las láminas infiltradas comienzan a decrecer rápidamente, con una tendencia de aproximación aguas abajo con el modelo 3 (SCS 92), este último asociado con los valores más bajos de las láminas de agua infiltradas (Cabecera del surco: 0,0273, ½ Ls: 0,02546 y Cola del surco: 0,01733) m3/m, por todo lo cual resultó descartado.
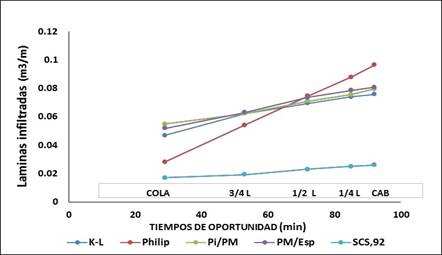
La figura 2 presenta el comportamiento de las láminas de agua infiltradas en función de los tiempos de oportunidad en cinco puntos de la longitud de los surcos, destacándose un similar comportamiento de los modelos 1, 4 y 5, a diferencia de los modelos Philip 2 y SCS 3. Estos últimos resultaron incoherentes, tal y como se aprecia en las figuras 1 y 2. Además, fueron confirmadas las limitaciones inherentes al método de Shepard et al. (1993), ya que no puede estimar con relativa precisión, el comportamiento de la distribución del agua en la longitud de los surcos para tiempos relativamente largos de riego. Esto se refleja en las bajas magnitudes de las eficiencias de los modelos 2 y 3, así como en el incremento de la eficiencia de aplicación (ΔEap) y pérdidas totales de agua (PT), tabla 4.
En la tabla 4 resultaron relevantes los resultados de los indicadores de calidad de desempeño del riego (eficiencias), correspondiéndose los valores mayores de las eficiencias de almacenamiento, (Ealm), aplicación (Eap) y distribución del agua (Ed), con los modelos 1, 4 y 5, con magnitudes menores para el modelo de Philip 2.
Por otra parte, resultó relevante el incremento de la eficiencia de aplicación causado por la condicionante de manejo del agua establecida, obteniéndose valores superiores para los modelos 1, 4 y 5, seguidos por el modelo 2, correspondiéndose las mayores pérdidas de agua (73 %) con los modelos de Philip y del SCS.
Para el modelo de Philip resultaron bajas las eficiencias de distribución del agua en el suelo y la uniformidad absoluta de su distribución (UAD). El comportamiento de los modelos 4 y 5 se corresponde con Holzapfel et al. (1988) citado por Díaz (2001), quienes comprobaron la dependencia de la infiltración con el perímetro mojado y su carácter bidimensional. Por último, los resultados obtenidos para la eficiencia de aplicación con los modelos 1, 4 y 5, se correspondieron con los reportes de Pérez (2013), en dichos suelos, para longitudes de surcos de 250 m y dosis neta parcial 30 mm.
En la tabla 5 se reportan las líneas de tendencia de mejor ajuste para cada uno de los cinco modelos de infiltración, resultando óptima la lineal con valores de R 2 muy satisfactorios, excepto para el modelo 3, tabla 5. Ratificándose para la evaluación de referencia, la inconsistencia de los resultados asociados con dicho modelo respecto al resto.
Se destaca el hecho de que, mediante las ecuaciones obtenidas, resulta posible estimar con precisión para cada modelo el comportamiento de la infiltración del agua en diferentes puntos del surco, en función de los respectivos tiempos de oportunidad (Nota: Tiempo de oportunidad = X).
Tabla 4 Resultados de los indicadores de desempeño del riego por surcos (eficiencias)
| Eficiencias / Modelos | 1. Kost - L. | 4. PM / Esp | 5. Pmi / PM | 2. Philip | 3. SCS |
|---|---|---|---|---|---|
|
|
96,3 | 96 | 96 | 91 | 42,6 |
|
|
61 | 60,6 | 60,4 | 57,7 | 27 |
|
|
77,3 | 77,2 | 71 | 64,6 | 81,3 |
|
|
65 | 64,7 | 62,3 | 47,1 | 71 |
|
|
17,5 | 17,4 | 17,2 | 14,6 | -16,2 |
| 39 | 39,4 | 39,4 | 73 | 73 |
Almacenamiento (Ealm), Aplicación (Eap), Distribución (Ed) y Uniformidad Absoluta de la Distribución (UAD).
Observaciones: 1) ΔEap (%): incremento de las eficiencias de aplicación con manejo del Tm = (56 % del Tinf de Zr) respecto a la condicionante tradicional (Tm = 100 % del Tinf de Zr). 2) PT: Pérdidas de agua totales (%) = PPP + PES, calculadas como: (100 -Eap).
Tabla 5 Estadígrafos de Ecuaciones de Infiltración
|
ESTADÍGRAFOS DE INFILTRACIÓN | ||
|---|---|---|
| Ecuaciones | Líneas de Tendencia (Mejor ajuste) |
|
| 1. Kost - Lewis | y = 0,0006x + 0,016 |
|
| 5. Pmi / PM | y = 0,0006x + 0,0158 |
|
| 4. PM / Esp | y = 0,0006x + 0,0127 |
|
| 2. Philip | y = 0,0009x + 0,0073 |
|
| 3. SCS. | y = 0,0001x + 0,0112 |
|
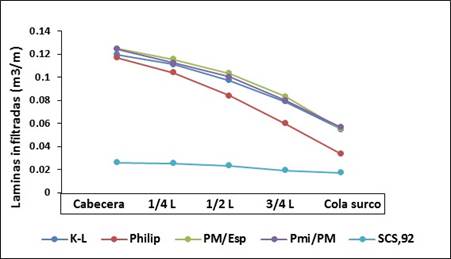
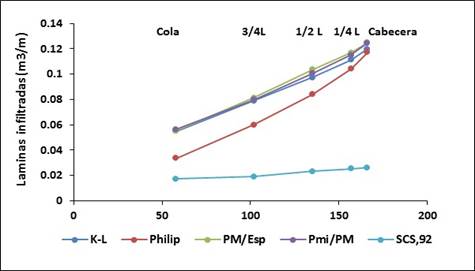
Respecto al segundo caudal evaluado (Qo = 4,4 L/s, Ls = 250 m y Zr = 35 mm), se manifestaron similitudes en cuanto al comportamiento de las láminas de agua infiltradas en las figuras 3 y 4, respecto a las de la evaluación anterior. También se reveló una tendencia de superioridad para los modelos 1, 4 y 5, consistente en el satisfactorio solapamiento de dichas láminas de agua, correspondiéndose con Kanya (2007). A lo que se agrega, una repetida incoherencia en los comportamientos de los modelos 2 y 3, acorde con Pérez y Jiménez (2018).
En la tabla 6 se constató el destacado comportamiento de la eficiencia de almacenamiento del agua para los modelos 1, 4 y 5, oscilando entre (98,4 y 98,7 %), mientras que, para la eficiencia de aplicación, los mejores resultados variaron entre (58,8 y 59,6 %). Resultó relevante, que los tres incrementos mayores de la eficiencia de aplicación (ΔEap) respecto al riego tradicional, oscilaron entre 14,2 y 13,4 % para los modelos antes citados, reduciéndose a un 7,8 % para el modelo 2 y -3,3 % para el modelo 3, el cual, debido a su comportamiento errático, resultó descalificado. Para el modelo 2 resaltaron las bajas eficiencias de la distribución del agua (Ed = 60 % y UAD = 41, 2 %).
Por último, se hallaron semejanzas en cuanto a criterios y modelos (1. Kostiakov - Lewis y 2. Philip) en los reportes de Osuna y Padilla (1998), mientras que Pérez (2013), reportó para dicho caudal en surcos de 250 m y dosis neta parcial 35 mm, una eficiencia de aplicación del 60 %, lo cual se corresponde con los resultados presentados en la tabla 6, modelos (1, 4 y 5).
Tabla 6 Resultados de los indicadores de desempeño del riego por surcos (eficiencias)
| Eficiencias / Modelos | 1. Kost - L. | 4. PM / Esp | 5. Pmi / PM | 2. Philip | 3. SCS 92 |
|---|---|---|---|---|---|
|
|
98,7 | 98,4 | 98,5 | 90 | 71,3 |
|
|
59,6 | 58,8 | 59 | 53,2 | 42,1 |
|
|
85 | 85 | 84 | 60 | 77,1 |
|
|
76,4 | 76,3 | 75 | 41,2 | 64,5 |
|
|
14,2 | 13,4 | 13,6 | 7,8 | -3,3 |
| 40,4 | 41,2 | 41 | 46,8 | 57,9 |
En la tabla 6 se aprecia que las mayores pérdidas del recurso hídrico (PT) correspondieron a los modelos 2 y 3, con valores del 46,8 y 57,9 % respectivamente, calificándose de inadmisibles. A continuación, en la tabla 7, los estadígrafos de infiltración presentaron una tendencia óptima de tipo potencial para el modelo 1 con R 2 = 0,9962, mientras que para los modelos 2, 4 y 5 fue de tipo lineal, con fluctuación de R 2 = (0,9926 - 0,9997), correspondiendo los valores más bajos con el modelo 3 con R 2 = 0,9819. Resultó destacada la importancia de las ecuaciones obtenidas para la estimación del comportamiento de la infiltración del agua en distintos puntos del surco, en función de los tiempos de oportunidad.
Tabla 7 Estadígrafos de Infiltración
|
ESTADÍGRAFOS DE ECUACIONES INFILTRACIÓN | ||
|---|---|---|
| Modelos | Líneas de Tendencia |
|
| 1. Kost - Lewis | y = 0,0117. x0,4155 |
|
| 5. Pmi / PM | y = 0,0005x + 0,0386 |
|
| 4. PM / Esp | y = 0,0004x + 0,0428 |
|
| 2. Philip | y = 0,0011x - 0,003 |
|
| 3. SCS. | y= 0,0031x + 0,0122 |
|
En relación con el tercer caudal evaluado (Qo = 5L/s y Ls = 380m y Zr = 40mm), según la tabla 2, para los tiempos de avance, mojado y aplicación o corte del agua, se observan valores mayores que los referidos para los anteriores caudales, debido a una muy superior longitud de surco y mayor magnitud de la dosis de riego requerida. Además, para el caudal de referencia, figuras 5 y 6, se evidenció una tendencia similar respecto a los caudales precedentes, correspondiéndose los mejores resultados de las láminas de agua infiltradas con los modelos 1, 4 y 5. Por su parte, el comportamiento del modelo 2 resultó deficiente, mientras que el modelo 3 se valoró como disfuncional en las condiciones de: caudal, longitud de surcos y suelos, similarmente a los reportes de: Pérez y Jiménez (2018) y Kanya (2007).
La tabla 8, muestra que los modelos 1, 4 y 5 ofrecieron los mejores resultados para las eficiencias de: almacenamiento entre (97,2 y 98 %), aplicación entre (54,4 y 54,6 %), distribución comprendida entre (71,6 y 72,4 %) y para la uniformidad absoluta de la distribución del agua entre (59,6 y 60 %). Lo anterior asociado a los mayores incrementos de la eficiencia de aplicación entre (8 y 8,1 %). Para el modelo de Philip, se obtuvo un bajo valor en cuanto al incremento de la eficiencia de aplicación (ΔEap = 4 %), asociado a pobres resultados de la distribución del agua (Ed) y (UAD), así como elevadas pérdidas totales del recurso agua (49,4 %). Por último, los resultados asociados al modelo 3, con pérdidas totales del (65,8 %), fueron considerados inadmisibles. Los resultados de la eficiencia de aplicación con el modelo 1, presentaron correspondencia con los reportes y criterios de Pereira et al. (2010) y Pérez et al. (1989). Este último en idénticas condiciones de suelo, lugar y longitudes de surcos.
Tabla 8 Resultados de los indicadores de desempeño del riego por surcos (eficiencias)
| Eficiencias / Modelos | 1. Kost - L | 4. PM / Esp | 5. Pmi / PM | 2. Philip | 3. SCS 1992 |
|---|---|---|---|---|---|
|
|
97,2 | 98,0 | 98,0 | 90,5 | 50,8 |
|
|
54,4 | 54,6 | 54,6 | 50,6 | 34,2 |
|
|
72,4 | 72,0 | 71,6 | 58,7 | 76,0 |
|
|
60,0 | 59,6 | 59,6 | 42,0 | 64,5 |
|
|
8,0 | 8,1 | 8,1 | 4,1 | -12,5 |
|
|
45,4 | 45,6 | 45,4 | 49,4 | 65,8 |
En la tabla 9 se presentan los estadígrafos de infiltración, con una tendencia óptima de tipo lineal para los modelos mejores, con R 2 = (0,994 - 0,998), mientras que para los 2 modelos restantes fue de tipo potencial, con fluctuación de R 2 = (0,938 - 0,993), correspondiendo los valores más bajos al modelo 3.
Tabla 9 Estadígrafos de infiltración
|
ECUACIONES DE INFILTRACIÓN | ||
|---|---|---|
| Modelos | Línea de Tendencia |
|
| 1. Kost - L. | Y = 0,0006x + 0,0197 |
|
| 5. PMi / PM | Y = 0,0006x + 0,0188 |
|
| 4. PM / Esp | Y = 0,0006x + 0,0175 |
|
| 2. Philip. | Y = 0,0003. (x1,166) |
|
| 3. SCS. | Y = 0,0032.x 0,4032 |
|
CONCLUSIONES
Resaltó la fiabilidad del modelo de infiltración Kostiakov - Lewis (1) y de los otros dos modelos que lo incluyen: efecto de la relación entre el perímetro mojado medio y el espaciamiento entre surcos, así como, el que relaciona el perímetro mojado en un punto de la longitud del surco con el promedio, corroborándose, para las tres evaluaciones, la eficacia de la condicionante de manejo del agua establecida.
Para los caudales evaluados mediante los modelos 1, 4 y 5, se obtuvieron los mejores rangos de fluctuación para las eficiencias de almacenamiento y aplicación, Q = 3,2 L/s: (Ealm = 96,3 - 96 % y Eap = 61 - 60,4 %), Q = 4,4 L/s: (Ealm = 98,7 - 98,5 % y Eap = 59,6 - 59 %), Q = 5,0 L/s: (Ealm = 98 - 97,2 % y Eap = 54,6 - 54,4 %), mientras que la eficiencia de distribución (Ed) osciló entre (85 - 71 %).
Para cada caudal utilizando los modelos 1, 4 y 5, la línea de tendencia óptima predominante fue de tipo lineal (excepto para el modelo de Kostiakov - Lewis, Qo = 4 L/s), comprobándose su precisión y alcance para la predicción de las magnitudes de las láminas de agua infiltradas. Los rangos de fluctuación del coeficiente R 2 fueron: Qo = 3,2 L/s: (0,9997 - 0,9985), Qo = 4,4 L/s: (0,9962 - 0,9926) y Qo = 5,0 L/s: (0,998 - 0,994).