My SciELO
Services on Demand
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista Cubana de Informática Médica
On-line version ISSN 1684-1859
RCIM vol.10 no.2 Ciudad de la Habana July.-Dec. 2018
Artículo original
MIDAS: Computer application for the identification of exact and inaccurate microsatellites in genomic sequences
1Department of Biochemistry, ICPB “Victoria de Girón”, University of Medical Science, La Habana, Cuba
Microsatellites are tandem repeat, frequent and diverse short sequences in the genomes of all species, constituting important markers in multiple areas of genomics-based research. Associations of these markers have been found in a significant number of human diseases. Vaccine development has shown how pathogens can evade the immune response by simply altering the composition of repeat sequences in their genes. There are numerous computer applications for the detection of these sequences, but they do not meet all expectations due to the divergence of criteria and approaches applied to solving the problem of their detection. MIDAS implements a non-heuristic solution based on two combinatorial algorithms in series: the first one detects exact microsatellites, and the second one, if the model parameters allow it, extends the sequences to their optimal inaccurate version. The application has as input the genomic sequence in GBFF or FASTA format and its output provides the microsatellite positions in the genomic sequence, as well as sizes, alignments, flanks and other statistics. The algorithm is highly efficient and comprehensive, detecting all possible repeat sequences regardless of their nucleotide composition.
Key words: SSR; microsatellite; molecular marker; data mining; algorithms
Introduction
Microsatellites are short tandem repeat sequences (known by their acronyms STR for short tandem repeats or SSR for simple sequence repeat) with repetition units between 1 and 6 bps (some authors extend their definition up to 8 bps), which can be tracts of repetitions ranging from a few copies to hundreds of copies. These sequences are abundant in the eukaryotic genomes, mainly associated with, but not exclusive, to non-coding regions. They are also present in prokaryotes genomes, constituting important markers for the genotyping, classification and epidemiological control of species of interest 1. Among the main motivations for the study of these sequences are their participation in processes such as recombination and transcription regulation 2, and when found in coding regions they cause neurodegenerative conditions such as fragile X syndrome, Huntington's disease (HD), spinobulbar-muscular atrophy (SBMA), Haw River syndrome (DRPLA), spinocerebellar ataxias (SCA1, SCA2, SCA3, SCA6, SCA7, and SCA17), as well as some types of cancer 3,4. Vaccine development has shown how pathogens can evade the immune response by simply altering the composition of repeat sequences in their genes 5. It has been proved how microsatellite expansion and contraction in bacteria can regulate expression of specific genes or affect its coding sequence resulting in phase or antigenic variation. This is particularly advantageous in pathogenic bacteria at contingency loci, as a way to evade the defense strategies of its host 6,7) . As genetic markers they have been widely used in genetic population studies due to their high polymorphism as a consequence of their high mutation rates, allelic diversity, co-dominance and being selectively neutral. Its use in forensic medicine for the identification of persons and degree of kinship is also well known.
The microsatellites have been experimentally identified from genomic libraries of organisms of interest, inspecting thousands of clones by hybridization with microsatellite probes. In addition to their high cost, these methods contain the bias inherent in the composition of pre-selected sequence patterns. With the modernization and lower cost of sequencing technologies, along with collaborations for the public exchange of sequences such as GenBank, EMBL, DDBJ, among others, bioinformatics methods have taken supremacy, giving rise to numerous applications that implement algorithms oriented to this end. However, the very dynamics of these sequences, subjected to different evolutionary forces, their particular roles, as well as the particular interest of researchers in one or the other depending on their composition, general features and biological purpose, has led these bioinformatics applications to implement different computational criteria, and consequently, to show variations in their results 8,9. To cite a few examples, we find applications that extend their detection system to repeat regions with longer periodicities (i.e. minisatellites and satellites); others detect only exact repeats or with minimal variations defined a priori; others use preset dictionaries of microsatellites or detect regions of low complexity and then confirm those using established rules. Applications such as TRF, IMEx, START, SRF or TROLL (10, 11, 12, 13, 14) are examples of software widely used for mining these kind of sequences, implemented with different algorithmic criteria. The conclusion is that there is not a unique solution, the spectrum of applications is diversified according to the types of SSR of interest and the computational methods used, being reflected in result’s differences.
The application we present, MIDAS (MIcrosatellite Detection Assistant System), fulfills with the following general principles: 1st only exact or inaccurate microsatellites are detected (i.e. not composite nor complex tandem repeats with patterns between 1-8 bp); 2nd exact microsatellites are detected and then extended if their flanks show a high sequence similarity with the repetition pattern; 3st the exact detection is exhaustive (i.e. all possible patterns that could make up an SSR are taken into account); and 4th extension is done by local alignment providing an optimal solution according to pre-determined alignment parameters.
The following section, Methods, describes in detail the sequence of steps followed by the application, algorithmic fundamentals, particular solution proposed to the problems of inaccurate detection of SSRs, and examples of detection of exact and inaccurate SSRs. It also describes the parameters and input - output formats of the application.
In the Results section, it is exhibited and analyzed the outputs corresponding to the detection of SSRs for Salmonella enterica (subsp. enterica Serovar Cubana). The input parameters and output formats of the application are described too.
Methods
The procedure starts with the detection of an exact repeat sequence, i.e. without substitutions, insertions or deletions of bases. For this purpose, the Aho-Crasick automaton (ACA) is implemented in the first stage, which finds all the occurrences of words in a text from the construction of a word tree. In the proposed implementation, a tree is constructed that contains all the words, of sizes between 1-8 nucleotides (one of the parameters of the application allows setting the upper limit of this range), formed by combinations of the 4 nucleotide bases, and with the specificity that they do not themselves constitute repeat sequences (e.g. aaaaaa) and excluding its cyclic permutations. ACA computes the search for these occurrences efficiently in time proportional to the size of the text and without pre-processing it. The occurrences of adjacent identical words are spliced and their position recorded, establishing the exact repeats or "seeds" of possible inaccurate repeats. With this step, the algorithm behaves like any other application that detects exact repetitions in an exhaustive and deterministic way (Fig. 1 (I)). The limitations of programs that detect only these sequences are obvious in terms of the biological purpose pursued. Let's think, just as an example, of a repeat that has a simple modification in a base, in which case the program would detect two repeats of the same class separated by a base, when in fact they were part of the same repeat. The generalized version of this problem creates an infinite number of situations that are less trivial and complicated to exemplify, and constitutes the main motivation for the proposed solution. In short, it is a matter of detecting an exact repeat "seed", with a reasonable number of repetitions not occurring by mere chance, from which to detect, if it exist, the inaccurate repeat one of which it is part. If there is no such approximate or inaccurate extension, the corresponding exact repetition will be reported, in this case free of ambiguity.
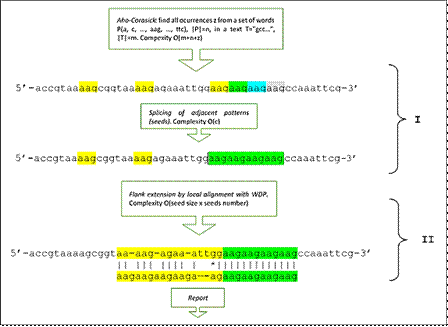
Fig. 1 Sequence of steps of the algorithm implemented in MIDAS in its two fundamental stages. (I) Detection of exact microsatellites (seeds), using word tree (Aho-Corasick) and subsequent splicing of occurrences. (II) Seed extension and detection of possible inaccurate microsatellite using dynamic programming.
The second stage of the algorithm solves the problem described above. The aim is to search for the possible inaccurate candidate from the flanks of the exact seed previously detected. Dynamic programming, i.e. the local alignment of the problem sequence, including flanks, against the repetition pattern, is used at this stage using the efficient wraparound technique (WDP, wraparound dynamic programming) (Fig. 1(II), Fig. 2). As is typical in sequence alignment methods, the optimal solution is dependent on the alignment parameters that define the weightings by coincidence, substitution or insertion/deletion of bases, which will ultimately determine the degree of conservation of the reported microsatellite.
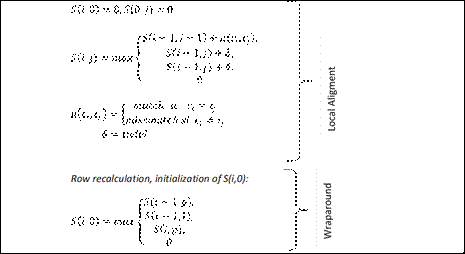
Fig. 2 - Recurrence that defines the algorithm of the second stage in MIDAS. It is a classic local alignment applying wraparound technique. Based on the repetition of the pattern, the gain in terms of time and space is established by allowing to align the problem sequence only with the pattern of the microsatellite. Match, mismatch (μ) and indel (δ) are the parameters for matches, substitutions or insertion/deletion respectively.
With respect to the extension per se there are two problems, which appear little explicit in the applications reported by other authors using sequence alignment, and which must be clarified and reasonably solved: 1st, how far do we extend on the flanks of sequence to report the alignment? When the sequence under study is relatively short the problem disappears if we use the all the sequence to find the optimal local repeat subsequence. In most cases this is not possible, think for example of a human chromosome with 200 million of base pairs, and thousands of candidate microsatellites in different regions of the genome. The solution presented by MIDAS is to use flank sizes of 3 times the seed size, and if the computed alignment covers more than 90 percent of the chosen sequence, the flank extension process is repeated and the sequence is realigned. In this way, we guarantee that the region to be extended to look for the inaccurate repeat is dynamic and does not exclude regions where it can continue to be extended. 2nd, How to evaluate if an alignment is adequate to decide to select it? This problem is inherent to all methods of sequence alignment and has been addressed in a variety of ways depending on the context. In applications for tandem repeats, some authors use the alignment score as selection criteria (this is the case of TRF). This approach is somewhat arbitrary, bearing in mind that while the score depends on the parameters of alignment, it also depends on the size of the alignment, and a certain bias is established that favors larger SSRs over shorter ones, being both equally important. In the case of MIDAS this problem disappears taking into account that the starting point is an exact SSR and the extension of the same will fall exclusively on the alignment parameters, in other words the application does not have the need to choose a priori an SSR establishing a cut-off value from the alignment score.
The alignment parameters are by default quite restrictive (Match=2, Mismatch=-5, Indel=-5), although the user has the option of using other more relaxed scoring schemes (4 in total) and then could debug SSRs at will by visual inspection. Figure 3 exemplifies the above with the results of the detection of two SSR in the same genome and with the same scoring scheme.

Fig. 3 Output of the program for two microsatellites located in two positions (separated by 379821 bp) of the genome vibrio cholerae IEC224 (NC_016944). The sequence pattern is the same in both as well as the number of exact repeat units (aag)4. The sequence in green is the exact SSR, in yellow the inaccurate extension and the rest are flanks. The alignment parameters were (Match=2, Mismatch=-3, Indel=-3). In (I) the program extended to a guanine (g) coincident in left flank, however in (II) there is a much greater extension that includes a substitution and five insertions or deletions of bases. Note that this extension would be reduced to an exact repetition if more restrictive parameters were used, (e.g. Match=2, Mismatch=-5, Indel=-5).
Results and Discussion
MIDAS is presented in its version 1.0 (binary) for Windows 32 and 64 bits platform (download v1.0.zip of the supplementary material) and its source code is written entirely in C++ STL compatible, so that it can be compiled for other platforms (Linux, Mac OS, etc.) using the appropriate compilers and libraries. It is a shell application, ideal for batch processing and linking to other applications (pipelines) by command line argument assignment. The application's arguments are three: 1th file name (genome to be scanned in FASTA or GBFF format, both single or multi-locus), 2nd maximum size of the repeat unit to be scanned and 3rd alignment parameter scheme for match, mismatch and indel, 4 in total, (2,-7,-7) (2,-5,-5,-7) (2,-5,-5) (2,-3,-5). As output, MIDAS returns three text files named equal the input file and with extensions .xls, .dat and .mfaa (the.xls could open directly with Excel or another spreadsheet application). The .xls file (Fig. 5) is in tabular format and its columns are: Pattern, Length (period), Start (initial position in the genome), End (final position in the genome), Score (alignment score), Matches (matching bases), Mismathces (non-matching bases), Indel (insertions and deletions of bases), Inaccuracy (% of inaccuracy of the repeat, measurement of imperfection of the repeat), 5' Flank (flank sequence to the 5’ end), 5' Entropy (compositional entropy in 5´ flank), 3' Flank (flank sequence to the 3´ end), 3' Entropy (compositional entropy in 3´ flank). Some developers of software for tandem repeats detection report the compositional entropy of the repeat region, this being obvious and mostly low. What allows a microsatellite to be used as a genetic marker is the variations in the number of copies and the uniqueness of flanks for its amplification in PCR techniques. MIDAS reports the entropy of the flanks, being these candidates for primer design in PCR technique, and giving a measure of how informative and unique they may be in the genome.
The file with .dat extension presents the previous data in a non-tabular form and allows the sequence alignment to be displayed. Finally, the file with extension .mfaa presents the detected microsatellites in multi-fasta format, with the repeat region marked in lower case and the flanks in upper case. This format allows batch processing with blastn (in Filter and Masking Options, mask lowercase letters checkbox), for the search of intra- and inter-species polymorphic candidates (Fig. 4). The header of this file presents information such as the GenBank access number, the pattern and the positions in the genome.
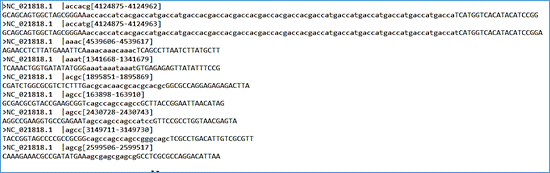
Fig. 4 - File format with extension .mfaa (multi-fasta with repeat region marked with lowercase letter).
The genome of Salmonella enterica (subsp. enterica Serovar Cubana str., access code NC_02181818) taken from the NCBI repository (https://www.ncbi.nlm.nih.gov/), was scanned with MIDAS and the results are shown above (Fig. 5). This genome has 4.977.480 base pairs and the computation time, including the creation of the output files, was less than 3 seconds. A total of 95 SSRs were detected, 2 hexa-, 14 tetra-, 70 tri-, 7 di- and 2 mono-nucleotides (number and repeat unit respectively) The detection parameters were: repeat unit <=6 and Match=2, Mismatch=-3, Indel=-3 (type 4 scheme of alignment parameters for the extension phase). The percentage of SSRs with tri-nucleotides (74%) is notable, which makes it suspicious of their location in coding regions, despite the fact that these regions predominate in bacterial genomes. The copy numbers show a range of 3 to 15, with an average of 5.8, for a coefficient of variation of 50%, highlighting among these the SSRs numbers 1 and 2 (hexa-nucleotides with 14 copies), 37, 75 and 76 (of tri-nucleotides with 13, 14 and 15 copies respectively) and 93 (of di-nucleotides with 13 copies).

Fig. 5 - Results of the detection of SSRs in the genome of Salmonella enterica (subsp. entericaSerovar Cubana str., access code NC_021818). This representation is the one shown in the output file with .xls extension.
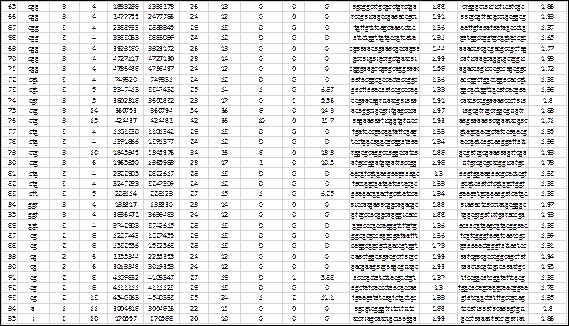
Fig. 5 (cont.) Results of the detection of SSRs in the genome of Salmonella enterica (subsp. entericaSerovar Cubana str., access code NC_021818). This representation is the one shown in the output file with .xls extension.
The average compositional entropy of the 5´ and 3´ flanks is 1.86 and 1.88 respectively, which can be considered high due to their proximity to 2 (maximum value). Among these, the most outstanding are 3´ flank of SSR No. 23 and 5´ flank of SSR No. 30, both with maximum compositional entropy.
Conclusions
In this paper we present MIDAS, an application for detection of accurate and inaccurate microsatellites (SSRs). The algorithm is fully combinatorial and has two general stages or procedures: 1st detection of exact SSRs by the technique of exact text patterns recognition and 2nd extension of them by means of dynamic programming technique. The result, and a brief analysis, of these sequences in the genome of Salmonella enterica (subsp. enterica Serovar Cubana) are shown. The application is efficient and intuitive, featuring low runtimes (processing 4,977,480 bp in 3 sec.) and a minimum number of input parameters which makes it more users friendly. It presents descriptive, tabulated and bioinformatic output formats that allow an easy and very complete visualization for the analysis of the results, also allowing the linking of these with other applications, for example extraction of annotated features in GenBank or detection of polymorphisms through extensive BLAST database searches.
Referencias
1. Liang S, Watanabe H, Terajima J, Li C, Liao J, Tung S, Chiou C. Multilocus Variable-Number Tandem-Repeat Analysis for Molecular Typing of Shigella sonnei. JOURNAL OF CLINICAL MICROBIOLOGY 2007;45(11):3574-80. [ Links ]
2. Martin P, Makepeace K, Hill S, Hood D, Moxon E. Microsat instability regulates transcription factor binding and gene expression. Proc Natl Acad Sci USA. 2005;102(10):3800-4. [ Links ]
3. Mitas M. Trinucleotide repeats associated with human disease. Nucleic Acids Res. 1997;25(12):2245-54. [ Links ]
4. Arzimanoglou I, Gilbert F, Barber H. Microsatellite instability in human solid tumors. Cancer 1998;82(10):1808-20. [ Links ]
5. Moxon ER, Rainey PB, Nowak MA, Lenski RE. Adaptive evolution of highly mutable loci in pathogenic bacteria. Current Biology. 1994;4:24-33. [ Links ]
6. Moxon R, Bayliss C, Hood D. Bacterial contingency loci: the role of simple sequence DNA repeats in bacterial adaptation. Annu. Rev.Genet. 2006;40:307-333. [ Links ]
7. Bayliss CD, Field D, Moxon ER. The simple sequence contingency loci of Haemophilus influenzae and Neisseria meningitidis. J. Clin. Invest. 2007;107:657-662. [ Links ]
8. Grover A, Aishwarya V, Sharma PC. Searching microsatellites in DNA sequences: approaches used and tools developed. Physiol Mol Biol Plants 2012 Jan-Mar;18(1):11-19. [ Links ]
9. Leclercq S, Rivals E, Jarne P. Detecting microsatellites within genomes: significant variation among algorithms. BMC Bioinformatics. 2007;8:125. [ Links ]
10. Benson G. Tandem repeats finder: a program to analyze DNA sequences. Nucleic Acids Res. 1999;27:573-580. [ Links ]
11. Mudunuri SB, Nagarajaram HA IMEx: Imperfect Microsatellite Extractor. Bioinformatics. 2007;23:1181-1187. [ Links ]
12. Merkel A, Gemmell N. Detecting short tandem repeats from genome data: opening the software black box. Brief Bioinform. 2008;9:355-366. [ Links ]
13. Zhou H, Du L, Yan H. Detection of tandem repeats in DNA sequences based on parametric spectral estimation. IEEE Trans Inf Technol Biomed. 2009;13:747-755. [ Links ]
14. Castelo AT, Martins W, Gao GR. TROLL: Tandem repeats occurrence locator. Bioinformatics. 2002;18:634-636. [ Links ]
Received: June 06, 2018; Accepted: November 03, 2018










 text in
text in