My SciELO
Services on Demand
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Ingeniería Energética
On-line version ISSN 1815-5901
Energética vol.39 no.3 La Habana Sept.-Dec. 2018
TRABAJO TEÓRICO EXPERIMENTAL
Flux-based rotor position estimator for a switched reluctance motor in simulink
Estimador para la posición de motores de reluctancia conmutada basado en las concatenaciones de flujo
Luis Manuel Alvarez Tapia, Mario Morera Hernández
Universidad Tecnológica de La Habana, Cujae. Cuba.
ABSTRACT
In the present paper a flux-based rotor position estimation algorithm was implemented using the Simulink development suite. The aforementioned method was selected because of the simplicity, robustness and low computational complexity of the algorithm. The design was implemented in several blocks, where each one of them represents a different stage in the rotor position estimation algorithm. The results were tested on a mathematical model for the WEKA SR-30102 switched reluctance motor. In order to accurately model its behavior, the non-linearity of the motor was taken into account. The mathematical equations that describe the mechanical and electrical properties of the motor were used in order to model the corresponding effects that occur inside the machine. A closed-loop operation was used using a classical implementation of a PID controller. To validate the results the output of the rotor position estimation block was compared against the rotor position and the results were analyzed.
Keywords: flux linkage; sensorless; simulation; Simulink; switched reluctance motor.
RESUMEN
En el presente trabajo se implementó un algoritmo para la estimación de la posición de rotor en motores de reluctancia conmutada usando las concatenaciones de flujo en la herramienta de desarrollo Simulink. El método anteriormente mencionado fue elegido por su simplicidad, robustez y baja complejidad computacional. El diseño fue implementado en diferentes bloques, donde cada uno representa una etapa del proceso algoritmo. Los resultados fueron probados en un modelo matemático para el motor WEKA SR-30102. Con el objetivo de modelar precisamente el comportamiento del motor se tomaron en cuenta las no linearidades propias de este tipo de motor. Se usaron las ecuaciones matemáticas que describen el comportamient eléctrico y mecánico para modelar el comportamiento interno del motor. Se usó una implementación clásica de un controlador PID para la operación a la lazo cerrado del accionamiento. Para validar los resultados, la salida del bloque para la estimación de la posición se comparó con la posición real, analizando los resultados obtenidos.
Palabras clave: concatenaciones de flujo; estimación sin sensores; simulación; Simulink; motor de reluctancia conmutada.
INTRODUCTION
The switched reluctance motor is an electric motor in which torque is produced by the tendency of its rotor to move towards a position where the inductance of the excited winding is maximized. The origin of the reluctance motor can be traced back to 1842, but the “reinvention” has been possibly due to the advent of inexpensive, high-power switching devices. The reluctance motor is a type of synchronous machine. It has wound field coils of a DC motor for its stator windings and has no coils or magnets on its rotor. Both the stator and rotor have salient poles; hence, the switched-reluctance motor is a doubly salient machine [1,2].
It has several advantages that make it an important competitor among other widely used machines, such as direct-current motors, induction motors or even synchronous motors. We can point out its simple and low cost construction and the advantage that bidirectional currents are not necessary. Moreover, thermal losses appear only in the stator, which in fact is easier to cool down. Another important advantage is the speed-torque characteristic which is adjustable, making it possible to obtain high torque at low speed, thereby avoiding the use of gear boxes. It is also possible to make use of these motors at high temperatures and speed in comparison to other motors such as permanent magnet motors [1,3].
As previously mentioned, switched-reluctance machines are attractive since they are reliable, relatively cheap and they produce high torque at low speed. These characteristics make them suitable for different purposes, among others for direct-drive and actioning robots applications, where position and velocity of joints must be controlled. However, this kind of machine is not easy to control; even under experimentally-validated assumptions leading to some simplifications.
Firstly, the dynamic model is highly nonlinear e.g., the generated electromagnetic torque is a complicated function of the electric currents and rotor positions. Secondly, reliable and accurate indirect sensing methods for the mechanical variables are fundamental in the development of low-cost, high-performance switched-reluctance motors. On one hand, the use of mechanical sensors increase the cost of the set-up and on the other, velocity sensors are often contaminated with noise. Therefore, avoiding the use of angular velocity and position sensors which is well known as sensorless control, is beyond pure theoretical interest.
Literature on sensorless adaptive control on other class of electrical machines is rich. For instance, in [4], an adaptive observer of flux, velocity, load torque and resistance of an induction motor is presented and practical stability based on Lyapunov theory is guaranteed, experimental validation is presented as well. In [5], is presented an adaptive high gain interconnected observer which is only supplied by the measurements of electrical currents and voltages of the permanent magnet synchronous motor, this observer estimates the rotor speed, the position, the stator resistance and the load torque.
In [6], a sensorless speed control for interior permanent magnet synchronous motors is designed by combining a robust back-stepping controller with integral actions and an adaptive interconnected observer, sufficient conditions are given to prove practical stability of the closed-loop. A sensorless output feedback sliding-mode controller and observer are designed in order to drive the induction motor without using neither flux nor speed sensors, stability properties are guaranteed based in Lyapunov theory and experimental runs are presented as well. An interesting cascade and High-Gain Observers Comparison for Sensorless control of induction motor is presented in [7] and in [8].
The authors of [9], presented a sensorless control for switched-reluctance motors based on direct torque control. An interesting approach appears in [10], where without using optical or magnetic sensors, stored magnetic characteristic information is utilized in order to elucidate the mechanical position, the same approach is presented in [11].
A coordinate transformation of the current phases system is utilized in [12], to design a position observer; experimental result are also presented. Some work on non model-based control has been as well reported, in [13] and in [14], fuzzy logic-based sensorless control algorithms are described and experimental results are presented as well. In [15] neural networks have been applied to predict position from inductance. Likewise, in [16] an improved back propagate neural network with inductance input pretreatment for the rotor position estimator of switched-reluctance motor is proposed as well as a sensorless control algorithm.
For fully sensorless control, in [17,18], is given a controller where position and velocity are obtained from information about flux linkage and phase currents. In this avenue, sliding mode observers are common, for example, paper [19], deal with the velocity and position estimation problem, other works on sliding mode observers are [20-22], where experimental results are also included.
In this paper a flux-based Rotor Position Estimator for a Switched Reluctance Motor in Simulink was implemented. The aforementioned method was selected because of the simplicity, robustness and low computational complexity of the algorithm. Also the selected method allows the motor to operate in a large portion of the speed-torque characteristic, aspect that is desirable.
MATERIALS AND METHODS
Switched Reluctance Motor Model in Simulink
The SRM was modeled (Fig.1), as part of a system that integrates a closed loop speed controller, a phase activation scheme and a power converter.

Speed Closed Loop Controller
A classical PID controller was implemented and his behavior is mathematically expressed as shown in equation (1).
In figure 2, it can be seen the implementation a simple PID controller using a speed reference as an input.

Phase Activation Scheme
The SRM WEKA SR-30102 has a 2-bit optical sensor attached to the shaft, yielding three possible combinations, that is either one of the sensor outputs is ON or none of them are, the last case in which both of them are ON is physically impossible, due to the mechanical characteristic of the rotary disc. This behavior was modeled in Simulink using the rotor position signal and a digital logic to select the correct phase to be powered.
Power Converter
The power stage features an asymmetric half bridge power converter that uses two switches per phase, allowing high flexibility when implementing control strategies. Inside of the power converter module are implemented four different control strategies, that is, hysteresis current control, single pulse controller and open and closed loop PWM controllers.
Switched Reluctance Motor
Figure 3 (left) shows the model of the switched reluctance motor. In order to accurately model its behavior, the non-linearity of the motor was taken into account. The mathematical equations that describe the mechanical and electrical properties of the motor were used in order to model the corresponding effects that occur inside the machine. In figure 3 (right) it can be seen the implementation of such model. As it can be seen, there are two submodules that lay the foundation on which the method is based, that is, the electrical and mechanical equations.

The electrical equation can be derived as follows: the applied voltage to a phase is equal to the sum of the resistive voltage drop and the rate of the flux linkage per phase, as it can be seen in equation (2).
Neglecting the mutual inductance between the phases equation 2 can be expanded, for phase A, as shown in equation (3).
Reorganizing and integrating ![]() in equation (3) we have equation (4).
in equation (3) we have equation (4).
Where, ![]() is the phase voltage,
is the phase voltage, ![]() is the phase resistance,
is the phase resistance, ![]() is the phase current,
is the phase current, ![]() is the inductance,
is the inductance, ![]() is the back-emf and
is the back-emf and ![]() is the rotor speed.
is the rotor speed.
Using the aforementioned equation, the electrical module was implemented (fig.4). The module is integrated by four blocks that contain the necessary information (flux linkage, torque, inductance, back-emf) to do the calculations. Each one of them is represented as a three-dimensional look up table (LUT) with the data stored in memory.

On the other hand, the mechanical equation (equation 5), is widely known, and was used to implement the mechanical block in Simulink (figure 5).

Sensorless Techniques
As was stated in the Introduction section, in this paper the flux linkage method was selected and was tested using a classical implementation of a PID controller.
In equation (1), phase voltage was defined as the sum of the resistive voltage drop and the rate of the flux linkage per phase. Isolating the flux linkage, and integrating, the equation remains as shown in equation (6).
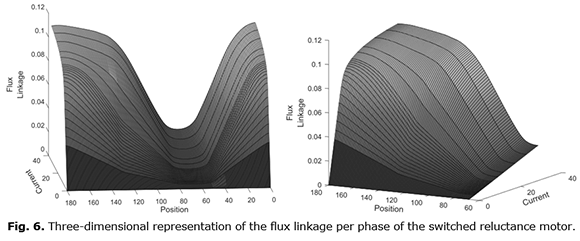
The flux linkage method calculates the flux linkage of SRM under different phase currents and rotor position. Thereafter, establish a three-dimensional table to store the data. The rotor position can then, be determined, by looking at the stored current and flux linkage values (figure 6 left). Although the method is simple for implementation purposes, it does require extensive characterization of the machine and medium to large amounts of memory.
Look up table implementation
The LUT implementation requires the use of the machine flux linkage tree-dimensional surface. The data can be obtained using either mathematical methods to generate approximations of the flux linkage curves [3,16], or using finite element analysis [2,8]. In either case the result is a three-dimensional LUT with the current, flux linkage and position data.
The first step was to select the data that will be used as the input for LUT. The goal is to replicate the relationship between the current, flux linkage and position with a one to one relationship between the first two variables and the third. Figure 7, shows that there is a two to one relationship between the variables, i.e. there are two flux linkage values for each pair of current and position. This happens because the SRM in question presents an irregular rotor, therefore the flux linkage surface it’s not symmetrical. This particular motor is designed to rotate in only one direction, therefore only one side of the flux linkage surface is needed (figure 6 right).
Figure 7 show the implementation of the algorithm in Simulink:

RESULTS
The results from the simulation of the Switched Reluctance Motor from section 2 and its control strategy are shown. Also, the rotor position estimation algorithm implementation is discussed, and then compared to the real values of the position.
To achieve this, an experiment was designed with the parameters presented on the table 1.

SRM Model in Simulink
In previous sections the Switched Reluctance Motor model implemented in Simulink was explained. In order to analyze its behavior, the electrical and magnetic parameters where measured.
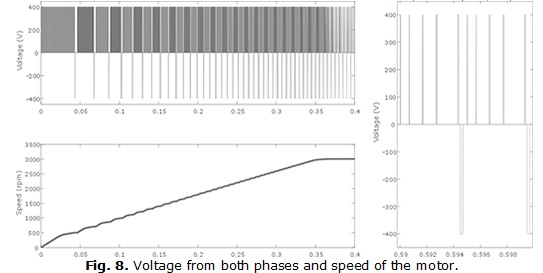
In the figure 8 (left), the voltage and speed are shown, on the right side a zoom was made on the former to observe the commutation of the phase voltage. The operation of the motor is described starting form standstill position until the motor reaches 3 000 rpm.
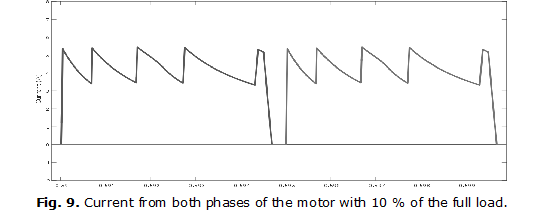
Applying the nominal voltage to phase (figure 9), using soft chopping modulation and current hysteresis closed loop control at 10 % of the full load, results in a peak current flowing through the windings of 5,2 A.
From the electromagnetic part of the analysis are the flux linkage and torque which can be seen in figure 10.

Flux based rotor position estimation algorithm
The calculation of the flux linkage using the current and voltage signals is the core of the rotor position estimation algorithm. figure 11, shows the real flux linkage vs the estimated one and the error of the calculation. As it can be seen the worst error is less than 3,2 %.

The next step is to assess the rotor position estimation. figure 12, shows the real position vs the estimated one and the error of the calculation. As it can be seen the worst error is less than 5 °, that represents less than 2,8 %.

CONCLUSIONS
In this paper, a position sensorless control strategy for high-speed SRM drives using a flux linkage method for the rotor angular position estimation has been proposed and tested. A reference flux linkage selecting principle was defined on the basis of FEM simulations. The motor speed and rotor position angle estimation equations were detailed. The experimental tests were performed in 4/2 pole SRM prototype, using the mathematical model implemented in Simulink. The results obtained demonstrate the feasibility, effectiveness and reliability of the proposed algorithm for both low- and high-speed SRM.
REFERENCES
[1].R. Krishnan. Switched Reluctance Motor Drives. CRC Press, 2001.Disponible en: http://ieeexplore.ieee.org/abstract/document/5186557/
[2].Kandipati Rajani. Modelling and control of switched reluctance motor. BSc Thesis, Vignan’s Engineering College, Vadlamudi, Guntur, 2011.disponible en http://ieeexplore.ieee.org/document/1546378/?denied
[3].K. T. Chau, "Switched Reluctance Motor Drives," in Electric Vehicle Machines and Drives: Design, Analysis and Application , 1, Wiley-IEEE Press, 2015, p.375-doi: 10.1002/9781118752555.ch5.Disponible en: http://ieeexplore.ieee.org/abstract/document/5186557/
[4].D. Traoré, J. De Leon, and A. Glumineau. Adaptive interconnected observer-based backstepping control design for sensorless induction motor. Automatica, 48(4):682 – 687, 2012. ISSN 0005-1098. Disponible en: https://www.sciencedirect.com/science/article/pii/S0005109812000349
[5].Marwa Ezzat, Jesus de Leon, and Alain Glumineau. Sensorless speed control of pmsm via adaptive interconnected observer. International Journal of Control, 84(11):1926–1943, 2011. doi: 10.1080/00207179.2011.629684. Disponible en: http://www.tandfonline.com/doi/abs/10.1080/00207179.2011.629684.
[6].Mohamed Assaad Hamida, Alain Glumineau, and Jesus de Leon. Robust integral backstepping control for sensorless {IPM} synchronous motor controller. Journal of the Franklin Institute, 349(5):1734 – 1757, 2012. ISSN 0016-0032.Disponible en: https://www.sciencedirect.com/science/article/pii/S0016003212000373
[7].M. Ghanes, J. De Leon, and A. Glumineau. Cascade and high-gain observers comparison for sensorless closed-loop induction motor control. Control Theory Applications, IET, 2(2): 133–150, 2008. ISSN 1751-8644. doi: 10.1049/iet-cta:20070058.Disponible en: http://digital-library.theiet.org/content/journals/10.1049/iet-cta_20070058
[8].M. Ghanes. Tracking performances of backstepping and high gain observers for sensorless induction motor control against low frequencies benchmark. In Control Applications, 2007. CCA 2007. IEEE International Conference on, pages 652–657, 2007. doi: 10.1109/CCA. 2007.4389306.Disponible en: http://ieeexplore.ieee.org/document/4389306/
[9].S. Kim, J. H. Kim and R. Y. Kimf, "Sensor-less direct torque control using inductance peak detection for switched reluctance motor," 2015 IEEE Conference on Energy Conversion (CENCON), Johor Bahru, 2015, p. 7-12. doi: 10.1109/CENCON.2015.7409505.Disponible en: http://ieeexplore.ieee.org/document/7409505/
[10].F. Peng, J. Ye and A. Emadi, "Position sensorless control of switched reluctance motor based on numerical method," 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, 2016, p. 1-8. doi: 10.1109/ECCE.2016.7855353.Disponible en: http://ieeexplore.ieee.org/document/7855353/
[11].J.A. Makwana, A. Mishra, P. Agarwal, and S.P. Srivastava. Sensorless control of switched reluctance motor drive: An analytical method. In Advances in Engineering, Science and Management (ICAESM), 2012 International Conference on, p. 571–576, 2012.Disponible en: http://ieeexplore.ieee.org/abstract/document/6216176/
[12].Jun Cai, Qing-Chang Zhong, and Zhiquan Deng. Estimation of srm rotor position based on coordinate transformation. In Industrial Electronics Society, IECON 2013 - 39th Annual Conference of the IEEE, p. 2786–2791, 2013. doi: 10.1109/IECON.2013.6699572.Disponible en: http://ieeexplore.ieee.org/abstract/document/6699572/
[13].Zhang Y, Liu C, Zhang L, “Sensorless control of SRM based on improved simplified flux-linkage method”, in 2014 17th international conference on electrical machines and systems (ICEMS), Oct. 2014, p. 722–726. DOI: 10.1109/ICEMS.2014.7013576.Disponible en: http://ieeexplore.ieee.org/document/7013576/
[14].Divandari M, Rezaie B, Askari-Ziarati B, “Torque estimation of sensorless SRM drive using adaptive fuzzy logic control”, in 2016 IEEE NW Russia young researchers in electrical and electronic engineering conference (EIConRusNW), Feb. 2016, p. 542–546. DOI: 10.1109/EIConRusNW.2016.7448241.Disponible en: http://ieeexplore.ieee.org/document/7448241/
[15].Paulson F, Prabhu VV, “Back propagation based ANN technique for rotor position estimation of 8/6 switched reluctance motor”, in 2015 international conference on innovations in information, embedded and communication systems (ICIIECS), Mar. 2015, p. 1–5. DOI: 10.1109/ICIIECS.2015.7192853.Disponible en: http://ieeexplore.ieee.org/document/7192853/
[16].R. Zhong, Y.B. Wang, and Y.Z. Xu. Position sensorless control of switched reluctance motors based on improved neural network. Electric Power Applications, IET, 6(2):111–121, 2012. ISSN 1751-8660. doi: 10.1049/iet-epa.2011.0092.Disponible en: http://digital-library.theiet.org/content/journals/10.1049/iet-epa.2011.0092
[17].D. Aliamkin, A. Anuchin, M. Lashkevich and F. Briz, "Sensorless control of two-phase switched reluctance drive in the whole speed range," IECON 2016 - 42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, 2016, p. 2917-2922. doi: 10.1109/IECON.2016.7793719.Disponible en: http://ieeexplore.ieee.org/document/7793719/
[18].Ma QQ, Liang WH, Ferreira FJTE, Bi DQ, Ge BM, “Improved flux linkage method for position sensorless control of high-speed SRM”, in 2014 international conference on electrical machines (ICEM), Sep. 2014, p. 783–788. DOI: 10.1109/ICELMACH.2014.6960270.Disponible en: http://ieeexplore.ieee.org/document/6960270/
[19].P. Brandstetter and P. Krna. Sensorless control of switched reluctance motor using sliding mode observer. In Applied Electronics (AE), 2013 International Conference on, p. 1–4, ISSN:1803–7232, 2013.Disponible en: http://ieeexplore.ieee.org/abstract/document/6636477/
[20].Xiao Wang, Fei Peng and A. Emadi, "A position sensorless control of switched reluctance motors based on sliding-mode observer," 2016 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, 2016, p. 1-6. doi: 10.1109/ITEC.2016.7520312.Disponible en: http://ieeexplore.ieee.org/document/7520312/
[21].Ouddah N, Loukkas N, Chaibet A, Boukhnifer M, Monmasson E, “Experimental evaluation of second sliding modes observer and extended kalman filter in a sensorless robust control of switched reluctance motor for EV application”, in 2015 23th mediterranean conference on control and automation (MED), Jun. 2015, p. 986–992. DOI: 10.1109/MED.2015.7158886.Disponible en: http://ieeexplore.ieee.org/document/7158886/
[22].B. Hongfen, Z. Jingwei and Q. Junfeng, "Sensorless control of the fault-tolerant permanent magnet motor based on sliding mode observer," 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, 2016, p. 5623-5626. doi: 10.1109/CCDC.2016.7532003.Disponible en: http://ieeexplore.ieee.org/document/7532003/
Recibido: 1/4/2017
Aprobado: 1/11/2017
Luis Manuel Alvarez Tapia, Universidad Tecnológica de La Habana, Cujae. Cuba. E-mail:lalvarezt@electrica.cujae.edu.cu












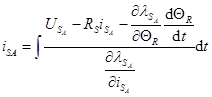 (4)
(4)