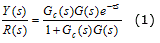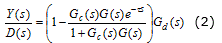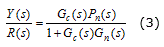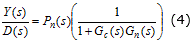My SciELO
Services on Demand
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Ingeniería Electrónica, Automática y Comunicaciones
On-line version ISSN 1815-5928
EAC vol.38 no.1 La Habana Jan.-Apr. 2017
ARTÍCULO ORIGINAL
Predictor de Smith: revisión y desafíos
Smith Predictor: review and challenges
Ivón O. Benítez-González, Raúl Rivas-Pérez
Departamento de Automática y Computación, Universidad Tecnológica de la Habana, La Habana, Cuba.
RESUMEN
En este trabajo se desarrolla una revisión del estado del arte del predictor de Smith, así como de sus modificaciones orientadas a mejorar sus prestaciones. Se muestran los avances históricos del predictor de Smith. Finalmente, se ofrecen algunos desafíos de la comunidad científica internacional para continuar mejorando las prestaciones del predictor de Smith en el control de plantas caracterizadas por presentar retardo de tiempo dominante.
Palabras claves: Predictor de Smith, retardo de tiempo, compensador de tiempo muerto, predictor de Smith modificado, perturbaciones medibles y no medibles
ABSTRACT
In this paper a review of the Smith predictor and its modifications oriented to improve its performance is developed. The historic progress of Smith predictor is shown. Finally, some challenges of the international scientific community to continue improve the performance of the Smith predictor in control of plants characterized by dominant time delay are offered.
Key words: Smith predictor, time delay, dead-time compensator, modified Smith predictor, measured and unmeasured disturbances
1.- INTRODUCCIÓN
Actualmente, existe un creciente interés en las estrategias de control de plantas con retardo de tiempo [1-3], debido a que el retardo de tiempo constituye un fenómeno muy común en el comportamiento dinámico de prácticamente todas las plantas industriales [4-6], unidades de procesos [7-10], sistemas ecológicos [11], agrícolas [12-14], biotecnológicos [15-17], etc. El retardo de tiempo es un fenómeno que se origina debido al desplazamiento temporal entre dos o más variables de una planta y puede ser generado por ejemplo, por el tiempo necesario para transportar masa, energía o información [18, 19]. El retardo de tiempo representa una significativa limitante en los sistemas control y debe ser considerado tanto en las etapas de análisis como en las de diseño de los controladores [20]. En general, el desempeño de los sistemas de control es muy sensible al retardo de tiempo [21, 22]. En la actualidad, el diseño de sistemas de control de plantas con retardo de tiempo constituye una fructífera línea de investigación con numerosas contribuciones, ver por ejemplo [10, 12, 13, 23-33].
El retardo de tiempo se define como el tiempo que transcurre desde que se realiza un cambio en las señales de entrada de una planta hasta que su efecto comienza a observarse en las variables de salida [4]. Durante ese intervalo de tiempo, la planta no responde en absoluto a las señales de entrada, y cualquier intento de manipular las variables de salida antes de que finalice el retardo conlleva inevitablemente al fracaso [34]. Objetivamente, las investigaciones en el campo del retardo de tiempo comenzaron en el siglo XVIII con los trabajos de D. Bernoulli, L. Euler, J. D’Alembert, dentro de un entorno meramente teórico, donde por primera vez se abordan las ecuaciones diferenciales con retardos [35]. Subsiguientemente, en [36, 37]se muestran los resultados de las investigaciones relacionadas con esta clase de ecuaciones, los cualesconstituyen la base del estudio del comportamiento dinámico de los sistemas (plantas) con retardo de tiempo.
Existen diferentes causas que originan el retardo de tiempo en las plantas industriales, entre las que se destacan: la distancia física entre el controlador y el instrumento de medición [38, 39]; el tiempo requerido por los actuadores para producir un cambio, por ejemplo válvulas o compuertas muy pesadas [40, 41]; el comportamiento dinámico intrínseco de algunas plantas, por ejemplo, el tiempo requerido por las reacciones químicas para obtener el producto deseado en los reactores químicos [15]; el tiempo exigido por los sensores para entregar las mediciones [42, 43]; el tiempo de procesamiento demandado por los controladores para obtener la señal de control [44, 45]; el tiempo necesario para la transmisión de información en las redes de comunicación [46, 47]; etc.
En las plantas MIMO el retardo de tiempo puede encontrarse en el vector de estado [30, 48], en el vector de control [49], en el vector de salida [50]y/o en los vectores de estado y de control de forma simultánea [18, 29]. El retardo de tiempo puede ser dominante o no dominante [2]. Las plantas presentan retardo de tiempo dominante cuando la relación τ/T>1, donde τ es el retardo de tiempo y T es la mayor constante de tiempo de la planta [18], en caso contrario (τ/T<1) el retardo de tiempo es no dominante [2]. El retardo de tiempo dominante es característico en el comportamiento dinámico de: plantas con transporte o transferencia de masa/energía, por ejemplo en la distribución de agua en canales de riego [38, 51]; plantas conectadas en serie [23]; plantas térmicas, entre las que se destacan intercambiadores de calor [24, 52, 53], hornos de calentamiento de combustible [25]y/o de recalentamiento de palanquillas [54], calderas [42]; plantas con fases de incubación, por ejemplo fermentadores [16, 17], etc.
El diseño de controladores apropiados para plantas con retardo de tiempo dominante requiere de un gran esfuerzo [27], debido a que las perturbaciones no se detectan a tiempo, la acción de control, que depende de la oportuna medición, no ocurre en el momento correcto, y demora en hacer efecto sobre el comportamiento dinámico de la planta [4]. Una respuesta retardada de la planta a la señal de control puede causar una reacción del controlador que no se corresponda con la requerida, lo cual puede originar la pérdida de estabilidad del sistema de control [20].
Desde la perspectiva del control clásico, el retardo de tiempo introduce fase negativa, la cual reduce la frecuencia crítica y el margen de fase, y por ende limita la máxima ganancia que se puede utilizar, así como la velocidad de respuesta de los sistemas de control [4]. Uno de los procedimientos utilizados para solucionar el efecto negativo del retardo de tiempo consiste en reajustar el controlador reduciendo la ganancia y aumentando la constante de integración, para de esta forma asegurar la estabilidad del sistema de control de lazo cerrado [2]. Sin embargo, ello conlleva a una respuesta temporal del sistema de control muy lenta, así como a un bajo rechazo a las perturbaciones, lo cual en diversos casos prácticos es inadmisible [28].
En la práctica, el retardo de tiempo puede ser invariante o variante en el tiempo [6], debido a que su valor depende de diversos comportamientos dinámicos. Los modelos que describen el comportamiento dinámico de plantas con retardo de tiempo pueden derivarse mediante la aplicación de herramientas de modelado [2]o de identificación de sistemas [13]. Usualmente, el retardo de tiempo variable se encuentra acotado [6].
Para el control de plantas con retardo de tiempo han sido propuestas diferentes estrategias. Cuando el retardo de tiempo es conocido y no es dominante es posible aplicar controladores convencionales, por ejemplo PID [20], obteniéndose un funcionamiento del sistema de control aceptable [55]. Sin embargo, el procedimiento de ajuste en línea del controlador PID es tedioso y requiere de mucho tiempo [20], por lo que en muchos casos el desempeño del sistema de control de lazo cerrado depende principalmente de la experiencia y del conocimiento del personal encargado del funcionamiento de la planta [56]. Es bien conocido, que muchos lazos de control de plantas industriales están pobremente ajustados [20], lo cual conlleva a la obtención de grandes pérdidas materiales y/o energéticas, baja calidad en los productos finales, etc. Por consiguiente, las técnicas de ajuste efectivo de controladores de plantas con retardo de tiempo son muy actuales y representan un reto para los investigadores [57].
Actualmente, uno de los principales desafíos que presenta el PID consiste precisamente en mejorar su degradado desempeño frente a plantas con retardo de tiempo dominante [58]. Por consiguiente, el diseño de controladores adecuados para el control efectivo de plantas con retardo de tiempo dominante constituye una importante línea de investigación con numerosas contribuciones y con un marcado interés de la comunidad científica internacional [2, 6, 13, 18, 34, 51, 59].
Las principales tendencias actuales en el control de plantas con retardo de tiempo se basan en el diseño de: controladores convencionales avanzados [33], controladores predictivos [52], controladores de orden fraccional [60], controladores por modelo interno [61], controladores robustos [62], controladores basados en técnicas de asignación finita del espectro (FSA) [63] o de reducción del modelo de Artstein [64], el predictor de Smith [65], así como sus múltiples extensiones [66].
El predictor de Smith (PS), propuesto en 1957 por el norteamericano Otto Smith [67] constituye sin lugar a dudas el compensador de tiempo muerto más utilizado en el control de plantas con retardo de tiempo debido a su elevada efectividad y simple implementación [68]. Esta estructura de control surgió con la idea de mejorar el desempeño de los controladores clásicos (PI o PID) en el control de plantas con retardo de tiempo dominante [20]. Su principal ventaja consiste en que elimina el retardo de tiempo de la ecuación característica del sistema de control en lazo cerrado, cuando su modelo interno describe de forma perfecta el comportamiento dinámico de la planta [68]. No obstante, esta estructura de control en su versión inicial presenta limitaciones, entre las que se destacan: no puede aplicarse en el control de plantas con integradores, inestables, o con retardo de tiempo variante en el tiempo; pobre desempeño frente a incertidumbres en el modelado de las plantas [69]; baja robustez frente a perturbaciones externas medibles o no medibles [18].
En los últimos 30 años se han desarrollado diversas contribuciones científicas dirigidas a mejorar el desempeño del PS convencional [23, 26, 70-85], siendo objeto de diferentes modificaciones (ver por ejemplo, [25, 33]) con el objeto de mejorar su capacidad de rechazo a perturbaciones medibles y no medibles, posibilitar su aplicación en el control de plantas inestables, permitir su uso en diversos entornos industriales, mejorar su robustez y facilitar el ajuste del controlador para aumentar su aplicabilidad.
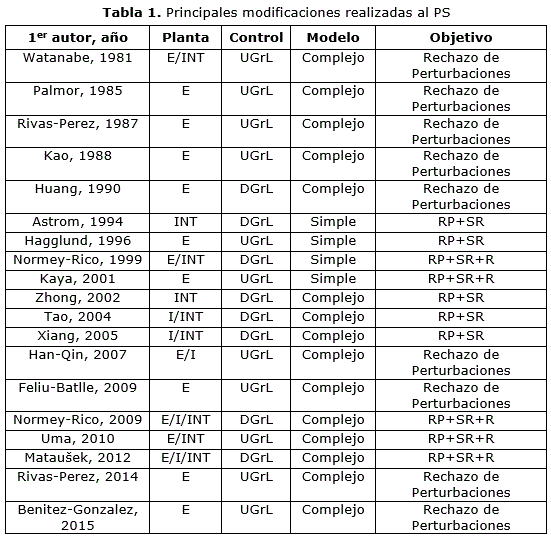
En la Tabla 1 se muestra un resumen en orden cronológico de las principales modificaciones realizadas al PS para su aplicación en el control de plantas SISO. Esta tabla constituye una versión actualizada de la tabla mostrada en [86]. En esta tablase utiliza la siguiente nomenclatura: tipode planta: estable (E), inestable (I), integrador (INT); tipo de estructura: un grado de libertad (UGrL) y dos grados de libertad (DGrL);modelo de la planta utilizado en el ajuste del controlador: modelo de primer orden (Simple) y modelo de cualquier orden (Complejo); objetivo de la modificación: para analizar o mejorar la robustez (R), para mejorar el rechazo al efecto de perturbaciones (RP), y para el seguimiento de la referencia (SR); metodología utilizada en ajuste del controlador: simple y con pocos parámetros (SIM) y compleja (COM).
Revisiones previas de compensadores de tiempo muerto han sido desarrolladas por Rivas-Perez [18], Palmor [4], O’Dwyer [87], Normey Rico y Camacho [68], entre otros. Una revisión de las principales modificaciones realizadas al PS en estos años permite clasificarlas en analíticas y estructurales. Dentro de las principales modificaciones analíticas están: el uso de aproximaciones para definir los modelos que describen el comportamiento dinámico de las plantas [88], la aplicación de expresiones analíticas para el ajuste de controladores [89], el uso de aproximaciones para representar el retardo de tiempo [2]y el uso de algoritmos de optimización para el ajuste de controladores [90]. Entre las principales modificaciones estructurales se encuentran: la introducción de realimentaciones internas [70], el uso de estructuras de control anticipatorio [68], el uso de estructuras de control en cascada [66], la introducción de observadores [91], el uso de filtros [33]y el uso de elementos de inteligencia artificial, sistemas expertos y de algoritmos bio-inspirados [92]. Sin embargo, es notorio destacar que en estas revisiones no se aborda la problemática relacionada con los retos y desafíos actuales del control de plantas con retardo de tiempo mediante la aplicación del PS.
El presente trabajo tiene como objetivos fundamentales: 1) desarrollar una revisión de las principales modificaciones realizadas al predictor de Smith (PS) para mejorar sus prestaciones; 2) analizar el desempeño de dichas modificaciones en su capacidad de rechazo al efecto de perturbaciones externas medibles y/o no medibles; 3) analizar los retos y desafíos actuales del PS y sus diferentes modificaciones en el control de plantas con retardo de tiempo dominante.
Este trabajo ha sido organizado de la siguiente forma: en la Sección 2 se presentan las principales modificaciones del PS para incrementar su desempeño frente a perturbaciones externas medibles y no medibles. En la Sección 3 se resumen las modificaciones del PS para controlar plantas con parámetros dinámicos variantes en el tiempo. En la Sección 4 se analizan las modificaciones del PS para el control de plantas inestables. Finalmente, en la Sección 5 se ofrecen las conclusiones.
2. -PREDICTOR DE SMITH MODIFICADO PARA EL CONTROL DE PLANTAS CON RETARDO DE TIEMPO DOMINANTE SOMETIDAS AL EFECTO DE PERTURBACIONES EXTERNAS
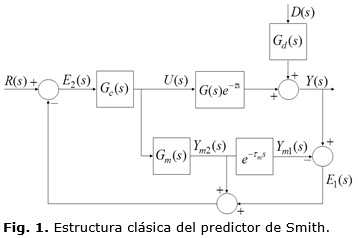
La estructura clásica del PS se muestra en la figura 1, la cual solo es aplicable a plantas estables con retardo de tiempo [67]. Esta estructura puede ser dividida en dos partes: el controlador (Gc(s)) y el predictor. La planta (Gp(s)=G(s)e-τs) se encuentra integrada por el actuador, el proceso con retardo de tiempo y el medidor-transmisor. El predictor está formado por un modelo rápido de la planta Gm(s)), sin retardo de tiempo, el cual posibilita calcular la predicción de la salida de la planta Ym2(s)), así como por un modelo completo de la planta que incluye el retardo de tiempo, es decir 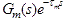 , cuya salida es la señal Ym1(s). Para que el sistema de control pueda corregir los errores de modelado, así como el efecto de las perturbaciones externas (D(s)), la salida del modelo completo de la planta (Ym1(s)) se compara con la salida de la planta (Y(s)) y la señal de error resultante (E1(s)) se realimenta hacia el controlador. Si se considera un modelo perfecto (Gm(s)=G(s)) y que no existen perturbaciones, la señal de error (E1(s)) entre la salida de la planta(Y(s)) y la salida del modelo completo (Ym1(s)) es cero, y el controlador(Gc(s)) puede ser ajustado, al menos en el caso nominal, utilizando el modelo de la planta sin retardo de tiempo. Esta estructura se caracteriza por presentar un pobre rechazo a las perturbaciones externas medibles y/o no medibles [2].
, cuya salida es la señal Ym1(s). Para que el sistema de control pueda corregir los errores de modelado, así como el efecto de las perturbaciones externas (D(s)), la salida del modelo completo de la planta (Ym1(s)) se compara con la salida de la planta (Y(s)) y la señal de error resultante (E1(s)) se realimenta hacia el controlador. Si se considera un modelo perfecto (Gm(s)=G(s)) y que no existen perturbaciones, la señal de error (E1(s)) entre la salida de la planta(Y(s)) y la salida del modelo completo (Ym1(s)) es cero, y el controlador(Gc(s)) puede ser ajustado, al menos en el caso nominal, utilizando el modelo de la planta sin retardo de tiempo. Esta estructura se caracteriza por presentar un pobre rechazo a las perturbaciones externas medibles y/o no medibles [2].
De la Figura 1 se definen las funciones de transferencia que relacionan la salida (Y(s)) con la entrada(R(s)) y la salida (Y(s)) con la perturbación (D(s)) para analizar cómo el PS responde frente a variaciones de la referencia o rechaza el efecto de perturbaciones, bajo la consideración de modelado perfecto:
Es importante señalar, que la estructura convencional del PS presenta el inconveniente de que si se ajusta el controlador para obtener una respuesta deseada frente a cambios en la referencia no se obtiene un buen rechazo al efecto de perturbaciones [68]. Siendo este un problema común que presentan todas las estructuras de control de un grado de libertad [2]. Además, esta estructura no se puede utilizar en plantas con integradores o inestables debido a que la misma internamente es inestable, por consiguiente, frente al efecto de perturbaciones el sistema de control se puede convertir en inestable. Por otro lado, pequeños errores en el modelo, por ejemplo cuando Gp(s) es diferente a Gm(s), pueden conllevar a la inestabilidad del sistema de control [4]. En [73] se analiza estabilidad de la estructura original del PS, demostrándose que cuando el controlador no se encuentra bien sintonizado, pequeños desajustes en el retardo de tiempo del modelo pueden conllevar a la inestabilidad del sistema de control, a pesar de que se disponga de elevados márgenes de fase y de ganancia.
Para intentar resolver estas limitaciones han sido propuestas diferentes modificaciones de la estructura clásica del PS, entre las que se destacan las modificaciones desarrolladas por Rivas-Perez et al. [18, 25, 29, 83, 93], Astrom et al. [71], Matausek y Micic [72], Normey-Rico y Camacho [2], etc. En [94-97] se proponen versiones discretas del PS, las cuales son más simples de implementar en la actividad práctica industrial.
En [26] se propone una modificación del PS para plantas sometidas a perturbaciones externas medibles, en la cual se adiciona un lazo de prealimentación. La principal limitación de esta modificación consiste en que se requiere disponer de un modelo adecuado del comportamiento dinámico de las perturbaciones.
En [83] se ofrece una modificación del PS de dos grados de libertad que posibilita desacoplar el problema de seguimiento de la referencia del rechazo al efecto de las perturbaciones externas no medibles. En [98], para aumentar la rapidez del rechazo al efecto de las perturbaciones externas no medibles, se propone una modificación del PS que incluye un filtro con una aproximación inversa del retardo de tiempo en bajas frecuencias. Sin embargo, las mejoras no son significativas cuando el retardo de tiempo es dominante.
En [88] se propone una estructura de control PI predictivo para procesos autorregulables con retardo de tiempo, la cual puede ser considerada como un caso especial del PS con tres parámetros de ajuste, de forma similar a los controladores PID. Esta propuesta posibilita ampliar su aplicación a plantas con retardo de tiempo dominante, pero incluye restricciones en su diseño. Esta propuesta se mejora en [86] mediante la aplicación de un filtro en la estructura del PS para aumentar su robustez frente a variaciones en los parámetros dinámicos de la planta. En [99] se propone una modificación del PS para plantas estables con ajuste automático basado en búsqueda numérica óptima de los valores de la ley de control. Su principal limitación radica en que solo es aplicable a plantas de primer orden.
La estructura PI predictivo filtrado prealimentado (FF-FPPI) presentada en [100] es una reutilización de las propuestas realizadas en [26, 86]para mejorar la velocidad de rechazo al efecto de las perturbaciones externas medibles sin afectar la capacidad de seguimiento y robustez del PS modificado. Además, en [100] se propone una segunda estructura que utiliza un controlador por modo deslizante combinado con el PS para aumentar la robustez frente a variaciones en la ganancia y en el retardo de tiempo de la planta. La principal limitación de la primera estructura consiste en que la perturbación debe ser medible, mientras que en la segunda se aumenta la complejidad en el diseño y las mejoras no son significativas frente a errores de modelado.
En [25] se ofrece una mejora de [83] donde se desarrolla una modificación analítica que amplía las posibilidades de aplicación del PS frente a perturbaciones externas no medibles. En [25] se compara el desempeño de varias modificaciones del PS para plantas estables de segundo orden y se demuestran las ventajas de la nueva modificación en diferentes posibles escenarios del comportamiento de las perturbaciones externas.
En [15] se realiza una propuesta de extensión de la modificación del PS sugerida en [71] para plantas con un integrador, posibilitando su aplicación en el control de plantas de segundo orden con retardo dominante. Esta modificación posibilita compensar, más rápidamente y con un mejor desempeño, el efecto de las perturbaciones externas no medibles.
2.1 .-MODIFICACIÓN DEL PS CON PREALIMENTACIÓN DE LA PERTURBACIÓN
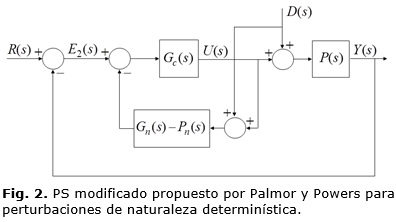
Entre las primeras modificaciones del PS, para plantas estables, se encuentra el trabajo desarrollado por Palmor y Powers [26] que incluye un lazo de prealimentación de la perturbación. El diagrama de bloques de esta estructura se muestra en la Figura 2.
Las relaciones Y(s)/R(s) y Y(s)/D(s) para esta estructura son:
De (4) se observa que el retardo de tiempo ha sido eliminado del segundo término de la ecuación (2), no siendo así en el caso del PS convencional, en el cual el retardo de tiempo sí está presente en el modelo nominal de la planta(Pn=G(s)eτs). La presencia de retardo de tiempo tiene como consecuencia que la respuesta temporal del PS, frente al efecto de perturbaciones externas, es más lenta que en la modificación presentada por Palmor y Powers [26]. Esta estrategia es aplicable solamente en plantas con perturbaciones de naturaleza determinística, lo que constituye una desventaja debido a que en algunas plantas el conocimiento del comportamiento de las perturbaciones resulta una tarea compleja. Además, para poder medir la magnitud de las perturbaciones es necesario contar con sensores, los cuales no siempre están disponibles.
Del análisis desarrollado se observa, que no obstante a los trabajos reportados, la problemática relacionada con el control efectivo de plantas con retardo de tiempo dominante sometidas a perturbaciones externas no ha sido totalmente resuelta debido al complejo comportamiento dinámico, en diversos casos, de las perturbaciones.
3. -PREDICTOR DE SMITH MODIFICADO PARA EL CONTROL DE PLANTAS CON RETARDO DE TIEMPO DOMINANTE CON PARÁMETROS DINÁMICOS VARIANTES EN EL TIEMPO
La problemática relacionada con el control de plantas con retardo de tiempo dominante y parámetros dinámicos variantes en el tiempo presenta un elevado interés [7], debido a que diversas plantas industriales presentan este tipo de comportamiento dinámico, ver por ejemplo [34, 51]. En esta categoría se incluyen también las plantas que exhiben retardo dominante variante en el tiempo. Para el control de esta clase de plantas han sido propuestas diferentes modificaciones del PS, las cuales se revisan a continuación.
En [101] se modifica la estructura original del PS, así como la propuesta realizada en [72] para ajustar en línea el retardo de tiempo variante en el tiempo de plantas estables utilizando como criterio la minimización de la función promedio de la diferencia de magnitud. En [76] se propone una modificación del PS con ajuste automático para plantas con dinámica estable, inestable o con integrador. En [102] se ofrece una solución para el control de plantas estables con retardo de tiempo variante en el tiempo, procesando el error entre la planta y su modelo para mejorar el rechazo de las perturbaciones, así como la robustez frente a variaciones del retardo de tiempo.
En [103] basado en los resultados previos de [71, 101, 104] se obtienen reglas de ajuste fundamentadas en un diseño robusto. En [105] se ofrece un sistema de control de dos grados de libertad para plantas inestables con retardo de tiempo que mejora los resultados obtenidos en [76]. El diseño y ajuste de estos controladores es complejo, por lo que su implementación se dificulta. Además, es importante resaltar que estos controladores son muy sensibles a errores de modelado. Otras reglas de ajuste con significado físico para esta clase de plantas se ofrecen en [106], en las que para el autoajuste de la estructura del PS se utiliza el método de relé con análisis de ciclo límite exacto para obtener el modelo de la planta. Una vez obtenido el modelo de la planta los parámetros de los controladores PI-PD del PS propuesto se obtienen de las expresiones que se presentan en [106], asumiendo un modelado perfecto.
Los observadores también han sido utilizados para el análisis de plantas con parámetros dinámicos variantes en el tiempo. Por ejemplo, en [78] se desarrolla un PS con un observador de perturbaciones externas. Posteriormente esta variante fue analizada en [107, 108] demostrándose que este método era aplicable en plantas estables y/o inestables. Versiones modificadas de esta estructura se pueden encontrar en [109-112], en las cuales se presentan reglas de ajuste y algoritmos más complejos para plantas con integrador y retardo de tiempo. Sin embargo, estas soluciones requieren de un modelo de la perturbación, lo cual limita su uso desde el punto de vista práctico.
En [113, 114] se proponen modificaciones de la estructura de control por modelo interno (IMC) para su aplicación en plantas inestables con retardo de tiempo incierto o no. En [113] se propone una estrategia que puede ser ajustada fácilmente logrando un compromiso entre las especificaciones temporales y las de robustez. En [114] mediante un esquema de control de dos grados de libertad se mejoran los resultados mostrados en [113], los cuales pueden extrapolarse a plantas con múltiples polos en el semiplano derecho cuando existen errores de modelado. En [115] para plantas inestables con integrador y retardo de tiempo, se modifica la propuesta de [76] eliminando la realimentación externa para separar el seguimiento de la referencia del rechazo de perturbaciones. La ventaja de [115] consiste en que se utiliza un controlador proporcional para estabilizar la respuesta frente a la señal de referencia. Para el seguimiento de la referencia se diseña un controlador óptimo H2 y para el rechazo a las perturbaciones se utiliza un estimador basado en el criterio integral cuadrático (ISE) como índice de desempeño.
En [79] se mejoran los resultados ofrecidos en [89] mediante una modificación del PS, muy similar a la estructura original, la cual presenta un ajuste simple y robusto e incluye dos filtros: uno en el error entre la planta y su modelo para mejorar el desempeño del PS y otro en la referencia para facilitar su seguimiento en plantas inestables de primer orden.
En [80] se ofrece un enfoque unificado para el diseño del PS que incluye varias de las modificaciones más recientes para su aplicación en plantas estables, inestables y con integrador que pueden tener cierta variación en sus parámetros. Esta propuesta posibilita desacoplar la respuesta al rechazo de perturbaciones externas del seguimiento de la referencia para cada tipo de planta y utiliza pocos parámetros para el ajuste del controlador.
El método de ganancia programada (GS - Gain Scheduling) es una técnica muy efectiva para reducir el efecto de las variaciones paramétricas [31], y es fácil de implementar mediante computadoras. Este método GS fue utilizado inicialmente en el control de plantas con variaciones solamente en la ganancia [116]. Mediante su aplicación es posible diseñar controladores que funcionan no solo alrededor de un punto de operación, como lo hacen los reguladores clásicos PID, sino además en el entorno de varios puntos de operación. De hecho, el método GS es una de las técnicas más utilizadas en los sistemas de control de vuelos [116]. Los controladores basados en GS se comportan de forma muy efectiva cuando se requiere controlar plantas con parámetros dinámicos variantes en el tiempo y/o no lineales [117, 118]. En [119] se propone un controlador que combina el método de ganancia programada convencional con el PS para el control de plantas con retardo de tiempo dominante variante en el tiempo. En los últimos años se observa una amplia aplicación de esta clase de controladores en la solución de diferentes problemas de carácter teórico y práctico [120, 121]. Sin embargo, los sistemas con GS convencionales no garantizan la estabilidad frente a cambios bruscos en los parámetros del modelo de la planta [12]. Para superar esta deficiencia han sido propuestos controladores basados en GS con variación lineal de parámetros (LPV-GS), los cuales posibilitan el control de plantas con variaciones dinámicas suaves o discontinuas [31]. Este método garantiza la estabilidad en lazo cerrado basándose en el concepto de estabilidad cuadrática [122] para todas las trayectorias reales de los parámetros dentro de una región dada. Esta metodología permite emplear el criterio multi-objetivo (H∞, H2, asignación de polos). Bajo condiciones adicionales, tales problemas de síntesis pueden ser transformados en problemas de optimización convexa, involucrando desigualdades de la matriz lineal. Esto conlleva a un problema condicionado y computacionalmente tratable para el análisis, cuando las condiciones de la matriz lineal dependen del vector de parámetros del sistema en forma multiafin. En [31] se ofrece un controlador LPV-GS combinado con un PS para el control de una planta con retardo de tiempo dominante y parámetros variantes en el tiempo. Sin embargo, la implementación práctica de este tipo de controladores presenta serias dificultades.
Un reto actual en el diseño de controladores de plantas con retardo de tiempo es el control por rechazo activo de perturbaciones (ADRC). Las soluciones basadas en ADRC para el control de plantas con retardo de tiempo no dominante han ido creciendo, por lo que su extensión a plantas con retardo de tiempo dominante constituye un área de interés. En [91] se desarrolla una predicción de la salida de la planta sin retardo basada en PS, obteniéndose una solución predictiva ADRC. Además, utilizando la teoría clásica de control en el dominio de la frecuencia se realiza un análisis de estabilidad, demostrándose que se mejora la estabilidad frente a variaciones de los parámetros dinámicos de la planta. Esta variante es semejante a los observadores de perturbaciones aplicados en plantas con retardo de tiempo dominante [78, 107-112], aunque su principal ventaja y diferencia consiste en que no se requiere de un modelo de perturbación. Este nuevo enfoque es más robusto frente a incertidumbres paramétricas de la planta y perturbaciones externas.
En [51, 54, 58-60, 84, 123-127] para el control de plantas con retardo de tiempo dominante y parámetros dinámicos variantes en el tiempo se combinan diferentes estructuras del PS con controladores PID de orden fraccional (FOC). Sin embargo, aunque estos controladores aumentan la robustez del sistema de control frente a incertidumbres paramétricas, su implementación práctica es compleja debido al orden fraccional de sus componentes.
En [81] se presenta una solución para el control de plantas SISO con múltiples retardos de tiempo. Los autores extienden el PS filtrado analizado en [80] para obtener un controlador robusto a incertidumbres de hasta un 10 % en la ganancia y de hasta un 15 % en el retardo de tiempo. Esta variante, con pocos parámetros de ajuste, posibilita su implementación práctica debido a que se basa en una estructura discreta. El análisis es realizado para perturbaciones del tipo escalón de pequeña amplitud. No obstante, la estructura presentada logra mejorar el control de este tipo de plantas con respecto a soluciones anteriormente reportadas para plantas estables e inestables.
En [128] se ofrece una solución para mejorar la efectividad del PS en plantas con retardo de tiempo variante en el tiempo. Los autores proponen un método para estimar el retardo en línea frente a señales del tipo escalón, mediante un método de optimización de búsqueda de parámetros generalizados, utilizando una modificación del PS propuesta en [75]. Sin embargo, esta propuesta adolece del análisis de robustez y efectividad frente a perturbaciones externas. Además, solo se consideran variaciones del 5% del valor nominal del retardo de tiempo, lo cual limita su aplicación.
El estudio realizado muestra que una parte de las modificaciones realizadas del PS para su aplicación en procesos con parámetros dinámicos variantes en el tiempo han sido orientadas a plantas con retardo de tiempo no dominante. Además, en estas modificaciones se analizan de forma independiente la variación de los parámetros dinámicos y el efecto de las perturbaciones externas, por lo que continúa siendo una problemática de interés para la comunidad científica.
4. -PREDICTOR DE SMITH MODIFICADO PARA EL CONTROL DE PLANTAS INESTABLES CON RETARDO DE TIEMPO DOMINANTE
La temática relacionada con el control de plantas inestables con retardo de tiempo dominante ha sido abordada por diferentes investigadores debido a que este tipo de plantas son muy comunes en la industria [22]. Entre las plantas inestables se encuentran también aquellas cuyos comportamientos dinámicos se describen mediante integradores [129]. Es bien conocido, que las plantas inestables con retardo de tiempo dominante no se pueden controlar mediante controladores basados en la estructura convencional del PS [70]. En este campo han sido propuestas diferentes modificaciones del PS, las cuales se analizan a continuación.
En [70] se propone una modificación del PS para su aplicación en el control de plantas con un integrador, la cual posibilita eliminar el error en estado estacionario frente a perturbaciones del tipo escalón. Sin embargo, si el controlador es un PI se obtiene una respuesta temporal del sistema de control muy lenta.
En [71] se presenta una modificación del PS que mejora la propuesta realizada en [70] mediante una estructura que posibilita desacoplar el ajuste del controlador para la respuesta a un estímulo por la referencia de la respuesta a perturbaciones. Esta solución implica el ajuste de seis parámetros si la ganancia de velocidad es desconocida. Posteriormente, en [72, 130] se proponen modificaciones del PS que posibilitan el control de plantas de alto orden con integrador y retardo de tiempo dominante con un menor número de parámetros de ajuste del controlador. Estas soluciones se basan en adicionar una ganancia y un controlador PD en el lazo interno, los cuales permiten un buen rechazo a las perturbaciones, independientemente de la respuesta a un cambio en la referencia. La desventaja de estas modificaciones consiste en que se requiere resolver una ecuación en lazo cerrado que contiene retardo de tiempo, lo cual se dificulta cuando el retardo de tiempo es relativamente elevado. En [131] se desarrolla una modificación de la propuesta presentada en [71] que posibilita reducir el número de parámetros de ajuste de la estructura de control.
En [109] se analizan las ventajas y desventajas de las modificaciones propuestas en [70-72, 130, 132] y se clasifican las modificaciones del PS para plantas con integrador. Las modificaciones del PS en base a la forma de tratar la señal de error entre la planta y su modelo, se dividen en dos grupos: 1) PS independiente, y 2) PS dependiente. Además, en este trabajo se propone un PS independiente donde el diseño del controlador queda libre del problema de la estabilidad, debido a que el controlador formulado no depende de la salida actual de la planta. Sin embargo, en la respuesta temporal debido al efecto de la perturbación se obtiene un elevado pico máximo.
En [112] se propone una modificación del PS para plantas con integrador y retardo de tiempo dominante que utiliza solo dos parámetros de ajuste con significado físico, uno relacionado con la velocidad de respuesta al seguimiento de la referencia y otro con la velocidad de respuesta al rechazo de las perturbaciones. Sin embargo, en esta propuesta, a pesar de mejorarse la velocidad de rechazo al efecto de las perturbaciones comparada con el PID y el PS clásico, la amplitud de la perturbación en la respuesta temporal sigue siendo significativa, lo cual limita el desempeño del sistema de control. Para este tipo de plantas en [111] se propone una modificación del PS basada en un esquema de estimación rápida de las perturbaciones, la cual puede extenderse a plantas con doble integrador.
En [133] se presenta una modificación del PS para mejorar la capacidad de rechazo de perturbaciones en plantas inestables de primer orden con retardo de tiempo. En esta modificación se utilizan tres controladores: un controlador proporcional para estabilizar el modo inestable y los otros dos se diseñan en términos de especificaciones óptimas con un criterio cuadrático de desempeño (H2), a partir del criterio de la integral del error cuadrático (ISE). El seguimiento de la referencia se realiza en lazo abierto. Para el rechazo a las perturbaciones se utiliza un controlador con realimentación interna del error entre la planta y su modelo. Sin embargo, el análisis de robustez de la estructura propuesta se realiza para pequeñas variaciones (10%) de la ganancia y del retardo de tiempo.
En [105] se desarrolla una modificación del PS para mejorar su desempeño en el control de plantas inestables con integradores y retardo de tiempo dominante. En esta variante se utilizan cuatro controladores con diferentes objetivos, es decir un controlador adicional al de la estructura propuesta en [75] para eliminar el compromiso entre el rechazo a las perturbaciones y el seguimiento de la referencia. Además, se incluye un controlador proporcional derivativo, el cual acelera la acción de corrección frente a perturbaciones del tipo escalón.
En [134] se propone una modificación del PS para plantas inestables que mejora el rechazo a las perturbaciones y obtiene un mejor desempeño de los controladores, disminuyendo el número de parámetros de ajuste. Sin embargo, esta modificación es válida solo cuando el retardo no es dominante. En [89], motivado por la propuesta de [71], se realiza una modificación analítica del PS para disminuir la complejidad en el diseño de los controladores, además, se analiza la robustez de la estrategia propuesta frente a variaciones de los parámetros de la planta.
En [135] se propone un PS modificado para mejorar la capacidad de rechazo a perturbaciones externas periódicas en plantas estables e inestables con retardo de tiempo, considerando que la frecuencia de las perturbaciones es detectable. Se muestran resultados comparativos superiores a los obtenidos en [75] para perturbaciones constantes y periódicas, además, se analiza la estabilidad interna de forma explícita, pero no se estudia la robustez de la propuesta.
Otra variante de modificación del PS se presenta en [90], demostrándose que esta modificación puede analizarse como un controlador PID en serie con un filtro de segundo orden, definido por el retardo de tiempo y un parámetro ajustable. La optimización del controlador se realiza mediante un algoritmo de enjambre de partículas (PSO) para restricciones de robustez y sensibilidad al ruido medido.
Uno de los principales problemas de los métodos de diseño de compensadores de retardo de tiempo para plantas inestables consiste en que el controlador obtenido no se puede implementar en su estructura original y se debe utilizar otro equivalente [4]. La implementación discreta del compensador representa una solución efectiva y simple, ya que permite cancelar las raíces inestables.
De la revisión realizada sobre las modificaciones del PS para el control de plantas inestables con retardo de tiempo se observa, que las propuestas se caracterizan por tener al menos tres controladores lo que incrementa el número de parámetros a ajustar y dificulta su implementación práctica. Además, generalmente estas modificaciones son válidas cuando el retardo de tiempo no es dominante, lo cual limita su aplicación. Por consiguiente, el desarrollo de nuevas modificaciones del PS para el efectivo control de plantas inestables continúa siendo un tema de interés.
5. -CONCLUSIONES
En este trabajo se desarrolló una revisión del PS y sus diferentes modificaciones, las cuales intentan a resolver la problemática relacionada con el control efectivo de plantas con retardo de tiempo dominante. El interés en este tipo de estructura de control se debe a la enorme cantidad de plantas industriales que se caracterizan por presentar retardo de tiempo dominante, así como en la significativa popularidad del PS como compensador de tiempo muerto. El análisis desarrollado sobre el estado del arte de las modificaciones del PS revela que aún existen problemas no resueltos (de carácter teórico y práctico) que imposibilitan la obtención de un elevado desempeño en el control de plantas con retardo de tiempo dominante con esta clase de estructura de control. Además, la mayor parte de las modificaciones del PS propuestas tienen un carácter teórico y/o académico, por lo que no han sido implementadas en la práctica industrial y consecuentemente su efectividad no ha podido ser comprobada.
Las modificaciones realizadas hasta fecha a la estructura convencional del PS solo resuelven alguna de sus limitaciones, a pesar de la gran cantidad de investigaciones realizadas. Específicamente, existen soluciones que presentan dificultades para su implementación desde el punto de vista práctico, ya sea por su elevada complejidad (desigualdades matriciales lineales) o por tener expresiones matemáticas impropias como en el caso del PS con modelo interno. Además, existen modificaciones de carácter teórico que solo pueden ser aplicadas en plantas con retardo de tiempo no dominante, por ejemplo, en el control por rechazo activo de perturbaciones. Otras modificaciones teóricas intentan resolver de forma independiente la problemática relacionada con la robustez del PS frente a variaciones de los parámetros dinámicos y perturbaciones externas (medibles y no medibles).
Por consiguiente, la solución efectiva de las actuales limitaciones del PS constituye un importante desafío para la comunidad científica internacional. Ello implica, que resulta necesario el desarrollo de nuevas investigaciones encaminadas a mejorar el desempeño del PS en el control de plantas con retardo de tiempo dominante, variante en el tiempo y sometidas al efecto de perturbaciones externas medibles y no medibles. REFERENCIAS 1. Ogata K. Modern control engineering. 5th ed. New Jersey: Pearson Education; 2010. 2. Normey-Rico JE, Camacho EF. Control of dead-time processes. Berlin: Springer; 2007. 5. Rivas-Perez R, Castillo-García F, Sotomayor-Moriano J, Feliu-Batlle V. Robust fractional order control of steam pressure in steam drum of bagasse boiler. Revista Iberoamericana de Automática e Informática Industrial. 2014;11(1):20-31. 6. González A, Sala A. Control predictor con ponderación de retardos: análisis de prestaciones y robustez ante retardo variable. Revista Iberoamericana de Automática e Informática Industrial. 2014;11(2):155-166. 7. Richard JP. Time-delay systems: an overview of some recent advances and open problems. Automatica. 2003;39(10):1667–1694. 9. Deaecto GS, Bolzern P, Galbusera L, Geromel JC. H2 and H∞ control of time-varying delay switched linear systems with application to sampled-data control. Nonlinear Analysis: Hybrid Systems. 2016;22:43-54. 18. Rivas-Perez R. Automatic control of water distribution in irrigation systems. Dr. Thesis. All Russia Research Institute of Hydraulic Engineering and Land Reclamation A.N. Kostyakov; 1990. Disponible en: https://www.researchgate.net/profile/Raul_Rivas-Perez/publications?sorting=newest&page=9 19. Lei J, Khalil HK. High-gain-predictor-based output feedback control for time-delay nonlinear systems. Automatica. 2016;71:324-333. 20. Astrom K, Hagglund T. Control PID avanzado. Madrid (España): Pearson Educación; 2009. 22. Novella-Rodríguez DF, del Muro-Cuéllar B. Control of second order strictly proper unstable systems with time delay. Revista Mexicana de Ingeniería Química. 2011;10(3):551-559. 23. Normey-Rico JE, Sartori R, Veronesi M, Visioli A. An automatic tuning methodology for a unified dead-time compensator. Control Engineering Practice. 2014;27:11-22. 25. Rivas-Perez R, Feliu-Batlle V, Castillo-Garcia FJ, Benitez-Gonzalez IO. Temperature control of a crude oil preheating furnace using a modified Smith predictor improved with a disturbance rejection term. IFAC Proceedings Volumes. 2014;47(3):5760-5765. 26. Palmor ZJ, Powers DV. Improved dead time compensator controller. AIChE Journal. 1985;31:215-221. 29. Rivas-Perez R. Technological process control in main canals of irrigation systems, with application to irrigation systems of Cuba. Ph.D Thesis. Institute of Hydraulic Engineering and Land Reclamation of Ukrainian Academy of Agrarian Sciences; 1984. Disponible en: https://www.researchgate.net/profile/Raul_Rivas-Perez/publications?sorting=newest&page=12. 37. Bellman R, Cooke KL. Differential-difference equations. New York: Academic Press; 1963. 38. Rivas-Perez R, Feliu-Batlle V, Sanchez-Rodriguez L, Pedregal Tercero DJ, Linares-Saez A, et al. Identification of the first pool of the Imperial de Aragon main irrigation canal. Hydraulic Engineering in Mexico. 2008;23(1):71-87. 45. Freirich D, Fridman E. Decentralized networked control of systems with local networks: A time-delay approach. Automatica. 2016;69:201-209. 46. Rivas-Perez R, Feliu-Batlle V, Castillo-Garcia FJ, Sanchez-Rodriguez L, Linares-Saez A. Control oriented model of a complex irrigation main canal pool. IFAC Proceedings Volumes. 2014;4(1):2919-2924. 49. Rivas-Perez R, Kao TG, Franco Parellada C. Asymptotic stability analysis of nonlinear systems with time delay in the control. Revista de Ingeniería Electrónica, Automática y Comunicaciones. 1986;7(4):294-297. 50. Rivas-Perez R, Kao TG, Pichuguin ED, Nguen VD. State space reconstruction in multivariable plants with time-delay. Control, Cibernética y Automatización. 1989;22(2):30-35. 59. Castillo-Garcia FJ, Feliu-Batlle V, Rivas-Perez R, Sanchez-Rodriguez L. Time domain tuning of a fractional order PIα controller combined with a Smith predictor for automation of water distribution in irrigation main channel pools. IFAC Proceedings Volumes. 2011;44(1):15049-15054. 65. Smith OJM. A controller to over come dead time. ISA J. 1959;6(2):28-33. 67. Smith OJM. Close control of loops with deadtime. Chemical Engineering Progress. 1957;53(5). 79. Normey-Rico JE, Camacho EF. Simple robust dead-time compensator for first-order plus dead-time unstable processes. Industrial and Engineering Chemistry Research. 2008;47:4784–4790. 83. Rivas-Perez R, Cao TG, Franco Parellada C, Prokofiev VE. Automatic control systems of time delay plants. Control, Cibernética y Automatización. 1987;20(1):24-26. 86. Normey-Rico JE. Predicción para control. Doctorado Thesis. Universidad de Sevilla; 1999. Disponible en: https://repositorio.ufsc.br/bitstream/handle/123456789/81146/ES0027-T.pdf?sequence=1 predicció n para el control 92. Oliveira J, Boaventura-Cunha J, Oliveira PM. Disturbance rejection improvement for the sliding mode Smith predictor based on bio-inspired tuning. En: CONTROLO 2016: Springer; 2017;402:45-58. 93. Rivas-Perez R, Benitez-González IO, Feliu-Batlle V, Sotomayor MJ. Modified Smith predictor for control of industrial plants with external unmeasured disturbances. Electro-Electrónica. 2009;32(2):34-43. 100. Martínez J, Camacho O. Two new Smith predictor proposals for performance and robustness enhancement for systems with elevated time delay. Revista Técnica de la Facultad de Ingeniería. Universidad del Zulia. 2005;28(3):179-188. 103. Normey-Rico JE, Camacho EF. A unified approach to design dead-time compensators for stable and integrative processes with dead-time. IEEE Transactions on Automatic Control. 2002;47(2):299–305. 116. Astrom KJ, Wittenmark B. Adaptive control. 2nd ed. USA: Addison -Wesley; 1995. 117. Sira RH, Márquez R, Rivas EF, Llanes SO. Control de sistemas no lineales: linealización aproximada, extendida, exacta. Madrid: Prentice Hall; 2005. 118. Shamma JS, Athans M. Analysis of gain scheduled control for nonlinear plants. IEEE Transactions on Automatic Control. 1990;35(8):898-907. 120. Rugh JG, Shamma JS. Research on gain scheduling. Automatica. 2000;36:1401-1425. 124. Castillo Garcia F, Rivas-Perez R, Feliu Batlle V. Fractional IIalpha controller combined with a Smith predictor for effective water distribution in a main irrigation canal pool. IFAC Proceedings Volumes. 2008;41(2):14558-14563. 125. Feliu-Batlle V, Rivas-Perez R, Castillo-Garcia FJ. Robust fractional-order temperature control of a steel slab reheating furnace with large time delay uncertainty. In: IEEE Proceedings of International Conference on Fractional Differentiation and its Applications. Catania (Italy); 2014. 129. Normey-Rico JE, Camacho EF. Robust tuning of dead-time compensators for processes with an integrator and long dead-time. IEEE Transactions on Automatic Control. 1999;44(8):1597-1603. 135. Zhou H-Q, Wang Q-G, Min L. Modified Smith predictor design for periodic disturbance rejection. ISA Transactions. 2007;46(4):493-503. Recibido: 14 de noviembre del 2016
Aprobado: 23 de febrero del 2017