Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Mecánica
versión On-line ISSN 1815-5944
Ingeniería Mecánica v.13 n.3 La Habana sep.-dic. 2010
Modelo por elementos finitos de un tubo a presión interna con una grieta transversal parcial
Partial transverse crack modelling in pipes under internal pressure using finite elements
Freddy Enrique Rodríguez VillarroelI, Jorge Rodríguez MatienzoII
I. Instituto Pedagógico de Maturín, Estado de Monagas, Republica Bolivariana de Venezuela.
Email: fervsegundo@yahoo.com
II. Dpto. de Mecánica Aplicada, Facultad de Ingeniería Mecánica.
Instituto Superior Politécnico "José Antonio Echeverría" - CUJAE
Calle 114 #11901 e/119 y 127. Marianao. La Habana. CP 19390. Cuba.
Email: matienzo@mecanica.cujae.edu.cu
Resumen
La detección de defectos en tubos sometidos a presión interna es un aspecto poco estudiado. Uno de los problemas a resolver es el modelado de los defectos, en particular los del tipo grieta cerrada. La dinámica de un tubo con un fluido interno a presión implica dificultades adicionales al problema. Se presentan los principios y las ecuaciones necesarias para poder modelar por el método de los elementos finitos la presencia de una grieta transversal parcial en un tubo de paredes delgadas en varios escenarios: vacío, con un fluido interno y con un fluido a presión. El análisis modal es empleado para determinar los cambios en los parámetros del modelo y valorar la influencia de la grieta en los mismos. Se parte del experimento de S.M. Murigendrappa y S.K. Maiti, el efecto de la grieta está representado por una reducción de la rigidez a la flexión del tubo en la zona de extensión d, cuya extensión es determinada a partir del concepto de energía potencial de la deformación, planteado por A P. Bovsunovsky y V. V. Matveev.
Palabras claves: grieta cerrada, análisis modal, tubos, elementos finitos.
Abstract
Fail detection in pipes under internal pressure is a not enough studied matter. A main problem is fault modeling, particularly the closed crack type. The dynamic of a pipe filled with a fluid under pressure implies additional challenges. The equations and principles needed to obtain a finite elements model of a partial transverse crack in a thin walled pipe are shown in different sceneries: empty, filled with fluid and filled with fluid under certain pressure. A modal analysis is performed to obtain the changes in modal parameters and crack influence. The result shows a good agreement with those obtained by S.M. Murigendrappa and S.K. Maiti. The crack is modeled trough a reduction of bending stiffness in a reduced zone. Its extension is calculated using the principle of equal strain energy between the crack zone and the model, exposed by A P. Bovsunovsky and V. V. Matveev.
Key words: crack detection, modal analysis, pipes.
INTRODUCCIÓN
Un problema que ha ocupado a un gran número de investigadores en todo el mundo ha sido la determinación del estado técnico de los sistemas mecánicos. En la actualidad se dispone de un conocimiento acumulado que permite resolver este problema para los sistemas con partes móviles, en particular los sistemas con partes giratorias. No se puede decir lo mismo de los sistemas estáticos, entre los cuales se incluyen las estructuras, tanto civiles como mecánicas, las instalaciones de redes técnicas y otras. La ausencia de movimiento en estos sistemas implica el uso de fuentes externas de energía que permitan la medición de sus parámetros y la obtención de la información. Una extensa revisión de esta problemática se encuentra en [6].
Existen algunos trabajos sobre la detección de defectos tales como corrosión, grietas, etc. en tubos, fundamentalmente en los empleados en ductos de combustibles líquidos y gaseosos [11, 16, 17] que en general se basan en el uso del ultrasonido o técnicas más o menos tradicionales. Los métodos empleados en la detección de defectos en estructuras existentes en la actualidad tienen como característica principal su carácter local. Si bien para una gran cantidad de situaciones esto es técnicamente posible, en las estructuras o sistemas de gran volumen o extensión su uso es complicado y generalmente requiere de un gran consumo de tiempo y recursos. El uso de las vibraciones mecánicas se presenta como una herramienta muy atractiva para diagnosticar las estructuras. Se parte de la base que los defectos mas frecuentes en estas repercuten de manera significativa en la rigidez y prácticamente despreciable en la masa, por lo que es de esperar una variación en sus parámetros modales, en especial en las frecuencias naturales.
Es de particular importancia el contar con métodos apropiados de detección de defectos para ciertas industrias como la petrolera, donde la seguridad durante las operaciones es fundamental. De allí la pertinencia de las tecnologías que eviten fallas catastróficas en elementos de trasegado de crudo y sus derivados que se asocien a derrames, pues los mismos son causa de perdidas económicas, de impacto ambiental y en algunos casos de pérdidas humanas [7]. Para el monitoreo de estos sistemas de distribución y transporte de crudo se dispone de sistemas SCADA y las RTU. El termino SCADA usualmente se refiere a un sistema central que monitorea y controla un sitio completo o un sistema que se extiende sobre una gran distancia. La mayor parte del control del sitio es en realidad realizada automáticamente por una Unidad Terminal Remota (UTR) o por un Controlador Lógico Programable (PLC). Las funciones de control del servidor están casi siempre restringidas a reajustes básicos, los datos se presentan a un operador (humano) y a través del sistema éste controla el proceso. A pesar de estos sistemas han ocurrido accidentes en los cuales se ha derramado crudo debido a la ruptura de los poliductos, lo que expone la debilidad de los sistemas SCADA en la prevención de la ocurrencia de fallos no pronosticados. Las variables de control más comúnmente auditadas son presión, temperatura o volumen, las cuales no guardan siempre relación directa con el estado de la estructura. Cuando se detecta una disminución o aumento exagerado de alguna de ellas se supone la presencia de una ruptura o taponamiento según sea el caso. Generalmente no se conoce la localización y se gasta un gran esfuerzo en la ubicación visual y posterior tratamiento.
Contar con un procedimiento que posibilite la inspección y detección temprana de defectos estructurales en ductos sería de gran importancia. Para ello se debe estudiar profundamente el problema tanto teórica como experimentalmente. Se espera definir los modelos necesarios para representar la presencia de una grieta en una viga tipo tubo de paredes delgadas a presión interna empleando el método de los elementos finitos, sobre el cual se estudiará el uso de vibraciones mecánicas y el análisis modal para obtener información sobre la presencia del defecto del tipo grieta transversal parcial. Como referencia para el modelo se emplean los resultados planteados por Murigendrappa S.M., Maiti S.K en [16, 17].
DESARROLLO
La presencia de un defecto en su estado inicial, como puede ser una grieta por fatiga influye en los parámetros dinámicos. Es por eso que se propuso desde la década del 70 el empleo de las vibraciones en su detección, dado que en su estado incipiente se supone que se afectan la rigidez y el amortiguamiento del sistema, pero no de forma notable su masa, lo que presupone a su vez que varíe la frecuencia natural como se presenta en [12]. Esto hizo que el análisis modal fuera una de las primeras herramientas utilizadas en la detección de una grieta. Sin embargo los primeros trabajos [4, 6, 22] dieron resultados contradictorios en la relación frecuencia natural-grado del defecto, lo que incitó a seguir estudiando el problema.
El uso de modelos de representación de los sistemas con defectos, entre ellos los de elementos finitos es de gran importancia, y para tener un buen resultado se necesita una representación correcta de la grieta. Para ello se requiere:
- Determinar los parámetros geométricos que definen la grieta.
- Suministrar los datos teóricos que sustentan la simulación.
- Comparar contra valores experimentales.
Son interesantes en este aspecto los trabajos de Sinha-Frisweell [21], que emplea una zona triangular a ambos lados de la grieta con rigidez disminuida en modelo por MEF, los de Tian et al [8], con un resorte de rigidez propuesta anteriormente por Rizos-Aspragathos [20] y un modelo continuo de una viga aplicando la transformada wavelet, Palacz-Krawzuck, [17] que usan un resorte similar en un modelo continuo y el MAC y COMAC como métodos de análisis, Dado-Shpli [15] usan también el resorte en un modelo por elementos finitos y el análisis modal. Estos y otros trabajos que se encuentran en la literatura usan diferentes técnicas de análisis de los resultados y condiciones de contorno, están dirigidos en lo fundamental a vigas, algunos pocos a pórticos o estructuras más complejas, y se ocupan de grietas abiertas. El caso de una grieta cerrada ha sido menos abordado en la literatura por las dificultades adicionales que ello implica. Chondros-Dimarogonas-Yao [2] emplean un modelo continuo bi-lineal para reflejar el cierre y apertura de la grieta y el análisis modal, lo que es un proceso más complicado y que no representa una ganancia notable en calidad. Bovsunovsky-Matveev [1] emplean una zona de inercia reducida en una distancia d1 a ambos lados de la grieta, un modelo continuo y el análisis modal. Esta representación permite reflejar el comportamiento del sistema como sistema continuo y fue empleada también en [12] combinado con la transformada wavelet. Se considera como el más adecuado para abordar la situación tratada en este trabajo.
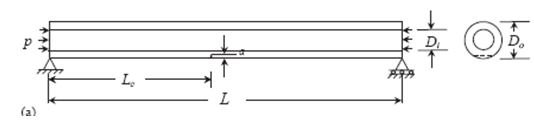
En [16] se realizó un experimento en tubos de paredes delgadas con una grieta transversal, Figura 1.
Figura 1, esquema del experimento [16]
En dicho trabajo se determinó la frecuencia natural del tubo vacío, lleno de agua y lleno de agua a presión, con y sin grieta. Los tubos eran de aluminio y acero al carbono.
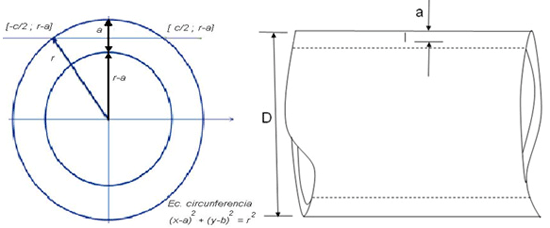
El experimento es modelado por elementos finitos, empleando el principio enunciado en [1]: el principio es reducir el momento de inercia en una extensión d1 determinada, de forma tal que la variación de la energía potencial de la deformación en esa zona sea equivalente a la producida por la grieta. Los parámetros de la grieta se definen en la Figura 2.
Figura 2, parámetros de la grieta a, b.
a. es la profundidad de la grieta
b. es la longitud de la recta de fondo transversal de la grieta.
c. radio exterior de la tubería.
d. diámetro exterior de la tubería.
La presencia de la grieta disminuye el momento de inercia de la sección transversal, y por lo tanto implica una variación de la energía potencial de la deformación en una distancia d1, ahora desconocida. Esta variación es (despreciando la variación del momento flector a lo largo del tubo):
![]() (1)
(1)
M: Momento Flector
Ic, nc: Momento de Inercia con y sin grieta.
E: Módulo de Young
d1: Extensión del sistema donde se calcula DU2
o sea, energía potencial para la flexión sin grieta (con Inc) menos energía potencial para la flexión con grieta (con Ic). Simplificando:
![]() (2)
(2)
La variación de la energía potencial de la deformación por la presencia de la grieta, de profundidad "a" y longitud de cuerda "c", [1], viene dada por:
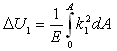 (3)
(3)
Donde k1 es el factor de intensificación de las tensiones (SIF) y A es el área de la grieta. Se determina a partir de:
![]() (4)
(4)
F1 depende de la configuración del objeto, en este caso un cilindro hueco, y la grieta. Se recuerda que el esfuerzo a flexión pura es:
![]() (5)
(5)
Se considera el punto más profundo de la grieta, entonces k1 se evalúa para "a", "c", etc. y alcanza un valor constante y determinado para la grieta, la energía potencial de la deformación por la grieta es finalmente:
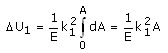 (6)
(6)
A= Área de la grieta.
Para la determinación de k1 y F1 según [14], se evalúan:
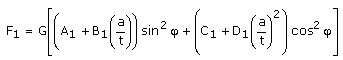 (7)
(7)
En esta expresión t es el espesor de pared, f es un parámetro que depende de si varía el ancho o la profundidad de la grieta con la carga. Se toma 10º para variación de la longitud y 90º para variación del ancho.
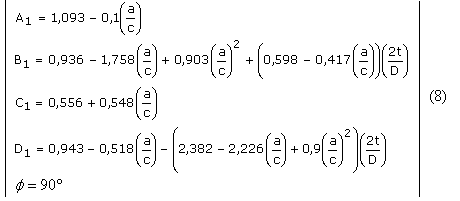
Además
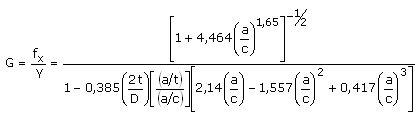 (9)
(9)
Finalmente U1 será:
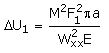 (10)
(10)
Para resolver las ecuaciones 7, 8 y 9 se toma:
![]() (11)
(11)
Igualando DU1 con DU2:
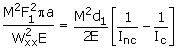 (12)
(12)
De donde d1 es:
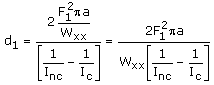 (13)
(13)
El módulo de la resistencia a la flexión Wxx es:
 (14)
(14)
La sección xx es la transversal del tubo quitando la grieta. Sustituyendo en 14:
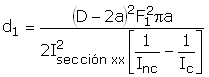 (15)
(15)
Es en la extensión 2d1 donde se reduce el momento de inercia, según las dimensiones de la grieta.
Sin embargo, a los efectos de un modelo por elementos finitos es más fácil construir un modelo de geometría (dimensiones) constante. La reducción de la inercia implica una reducción en la rigidez EI, que se define como EIc, para el caso de la presencia de la grieta, lo que se puede lograr conservando el valor el momento de inercia y variando el módulo de Young al valor adecuado.
Se tomó uno de los experimentos de [16], correspondiente al tubo de acero al carbono y se determinaron todos los valores necesarios.
Tabla 1. Parámetros de la grieta a modelar
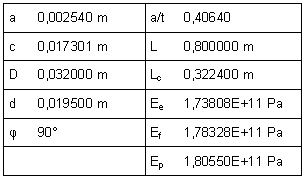
En la Tabla 1, Ee, Ef y Ep representan respectivamente el valor del módulo de Young para los casos de tubo vacío, lleno y lleno a presión. El parámetro j es necesario para el cálculo de F1. L y Lc son la longitud efectiva del tubo y la posición de la grieta respecto a un extremo respectivamente, t es el espesor de pared del tubo.
Luego de efectuados los cálculos para una profundidad de grieta dada, se obtiene:
Tabla 2. Parámetros del modelo
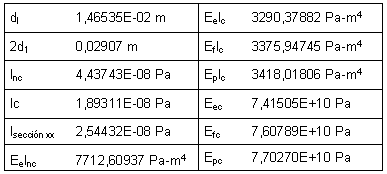
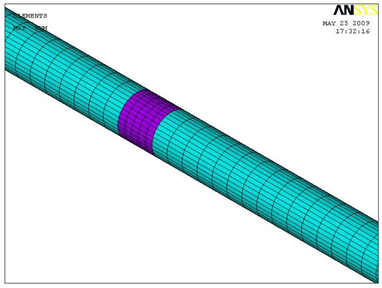
Aquí el subíndice c significa "con grieta" y nc "sin grieta". Con estos resultados se construyeron los modelos correspondientes por elementos finitos en ANSYS. Se seleccionó el elemento SHELL 63, por cumplir con la teoría de membranas y permitir la aplicación de presión interna. Los modelos se muestran en la Figura 3. La zona de color diferente es la que, en el caso de la simulación de la grieta, tiene un material de módulo de Young reducido, como se ve en la Figura 4. En todos los casos las restricciones en los extremos corresponden a articulaciones. Se hizo el análisis modal de todos los modelos para los primeros modos naturales de vibración y se compararon las frecuencias naturales obtenidas con las determinadas experimentalmente en [16] para los mismos modos. En [16] no se dan resultados para el primer modo, por eso no se incluye este modo en la Tabla 3.
Figura 3. Modelos por EF del tubo sin y con grieta
Figura 4. Detalle de representación de la grieta
Los resultados de las frecuencias naturales se muestran en la Tabla 3
Tabla 3. Frecuencias naturales, Hz
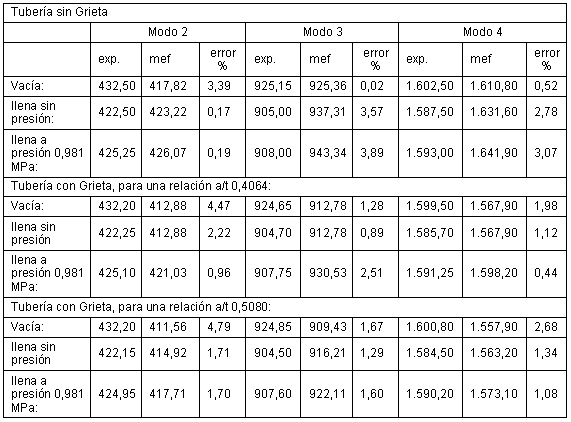
El tiempo de ordenador consumido no es excesivo, los modelos son relativamente simples de construir. De la Tabla 2 se observa que la zona de inercia reducida es de sólo 1,4 mm de extensión, por lo que se conserva el carácter local del defecto en el modelo. Tal como se reporta por varios autores [4, 6, 8, 9] la variación en la frecuencia natural para los casos sin y con grieta no es significativa.
Los resultados muestran una excelente correspondencia con los experimentales reportados en [16]. Los modelos reflejan adecuadamente la presencia del fluido en el interior, incluyendo el caso de fluido a presión, siendo el error relativo menor en esos casos. La profundidad de la grieta modelada no influye en los resultados.
CONCLUSIONES
El modelo del tubo con grieta parcial a presión interna elaborado por el método de los elementos finitos brinda resultados que se corresponden adecuadamente con los experimentales aportados por Murigendrappa [16]. El error en todos los casos está por debajo del 5%.
El error obtenido permite afirmar que el procedimiento seguido para representar la grieta planteado por Bovsunovsky [1], y el modelo por elementos finitos construido a partir del mismo, puede ser utilizado para el caso de grietas en tubos sometidos a presión, variando la rigidez de la sección en la cual se encuentra la grieta.
Estos resultados posibilitan el ensayo de métodos de detección de la presencia de la grieta de forma teórica, usando modelos confiables y abren un camino para una posterior experimentación.
REFERENCIAS
1. BOVSUNOVSKY, A. P. y MATVEEV, V. V. "Analytical approach to the determination of dynamic characteristics of a beam with a closing crack". Journal of Sound and Vibration. 2000. vol. 235, nº 3, p. 415-434.
2. CHONDROS, T. G.; DIMAROGONAS, A. D. Y YAO, J. "Vibration of a beam with a breathing crack". Journal of Sound and Vibration. 2001. vol. 239,
nº 1, p. 57-67.
3. CHONDROS, T. G. Y DIMAROGONAS, A. D. "Vibration of a beam with a breathing crack". Journal of Sound and Vibration. 2001. vol. 239, nº 1,
p. 57-67.
4. DOEBLING, S. W.; FARRAR CHARLES, E., et al. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review. 1996. p. 5-63.
5. EWINS, S. Modal testing: theory and practice. 2da ed. Prentice Hall, England, 2000. p. 1-154. ISBN 0-86380-218-4.
6. FARRAR CHARLES, R. y DOEBLING SCOTT, W. An overview of modal-based damage identification methods. Los Alamos National Laboratory Report A-13070-VA5, 2002. p. 92-106.
7. FRANCISCO, A.; RUMICHE, P. Y INDACOCHEA, J. E. "Estudios de Caso de Fallas y Accidentes en Gasoductos y Oleoductos". Joining Science & Advanced Materials Research Laboratory. [Consultado el: 6/4/2009].
Disponible en: http://www.exsa.com.pe/links/Estudiosdecasodefallasyaccidentesengaseoductosyoleoductos.pdf
8. JIAYONG, T.; ZHENG, L. Y XIANYUE, S. "Crack detection in beams by wavelet analysis of transient flexural waves". Journal of Sound and Vibration. 2003. vol. 261, p. 715-727.
9. KIM, J. T. Y STUBBS, N. "Improved damage identification method based on modal information". Journal of Sound and Vibration. 2002. vol. 252, nº 2, p. 223-238.
10. LALU, M.; IDICHANDY, V. G. Y GANAPATHY, C. "Structural monitoring of offshore platforms using impulse and relaxation response". Ocean Engineering. 2001. vol. 28, p. 689-705.
11. MAHJOOB, M. J. Y SHAHSAVARI, A. A. Vibration-Based Damage Detection Method for Pipes Conveying Fluid. En 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Honolulu, Hawaii. 23 - 26 April 2007.
12. RODRÍGUEZ MATIENZO, J. "Detección de la presencia de grietas cerradas en elementos tipo viga mediante la transformada wavelet". Ingeniería Mecánica. 2008. vol. 8, nº 1, p. 41-47.
Disponible en: http://www.cujae.edu.cu/ediciones/Revistas/Mecanica/Vol-11/1-2008/05_2008_01_41_47.pdf ISSN 1815-5944.
13. MICKENS, T.; SCHULZ, M.; SUNDARESAN, M., et al. "Structural health monitoring of an aircraft joint". Mechanical Systems and Signal Processing. 2003. vol. 17, nº 2, p. 285-303.
14. MIEDLAR, P. C. Selected Stress Intensity Factor Cases, Section 11.3. [Consultado el: 1/4/2009].
Disponible en: http://www.afgrow.net/applications/DTDHandbook/pdfs%5CSec2_6.pdf
15. MOHAMMAD H.F, D.;SHPLI, O. A. "Crack parameter estimation in structures using finite element modeling". International Journal of Solids and Structures. 2003. vol. 40, p. 5389-5406.
16. MURIGENDRAPPA, S. M.; MAITI, S. K., et al. "Experimental and theoretical studyon crack detection in pipes filled with fluid".
Journal of Sound and Vibration. 2004. vol. 270, p. 1013-1032.
17. MURIGENDRAPPA, S. M.; MAITI, S. K.;SRIRANGARAJAN, H. R. "Frequency-based experimental and theoretical identification of multiple cracks in straight pipes filled with fluid". NDT&E International. 2004. vol. 37, nº 6, p. 431-438
18. PALACZ, M.;KRAWCZUK, M. "Vibration parameters for damage detection in structures". Journal of Sound and Vibration. 2002. vol. 249, nº 5,
p. 999-1010.
19. PALACZ, M. "Vibration parameters for damage detection in structures". Journal of Sound and Vibration. 2002. vol. 249, nº 5, p. 999-101.
20. RIZOS, P. F.;ASPRAGATHOS, N. "Identification of crack location and magnitude in a cantilever beam from the vibration modes".
Journal of Sound and Vibration. 1990. vol. 138, nº 3, p. 381-388.
21. SINHA JYOTI, K.;FRISWELL MICHAEL, I. "Simulation of the dynamic response of a cracked beam". Computers and Structures. 2002. vol. 80,
nº p. 1473-1476.
22. VANDIVER, J. K. Detection of Structural Failure on Fixed Platforms by Measurement of Dynamic Response. En 7th Annual Offshore Technology Conference. 1975. p. 243-252.
Recibido el 24 de junio de 2010
Aceptado el 28 de octubre de 2010