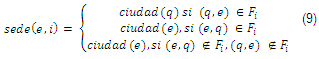My SciELO
Services on Demand
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Ingeniería Mecánica
On-line version ISSN 1815-5944
Ingeniería Mecánica vol.16 no.3 La Habana Sept.-Dec. 2013
ARTÍCULO ORIGINAL
Reducción del costo de transportación en las Series Nacionales de Béisbol de Cuba empleando metaheurísticas
Metaheuristics for the reduction of transportation cost in Baseball National Series
Alejandro Rosete-Suárez, David Paredes-Miranda, Eduardo Sánchez-Anzola
Instituto Superior Politécnico José Antonio Echeverría. Facultad de Ingeniería Informática. La Habana. Cuba
RESUMEN
El costo de transportación de las Series Nacionales de Beísbol en Cuba incluye los movimientos de los equipos entre las distintas provincias. La distancia total recorrida depende del calendario de la competencia que define el orden de los juegos. Hasta el año 2012, estos calendarios fueron construidos manualmente. El objetivo de este trabajo fue demostrar como puede reducirse la distancia total recorrida, mediante el uso de metaheurísticas. Fue necesario plantear todos los aspectos que definen el problema de optimización correspondiente. Luego, se compararon varias metaheurísticas en este problema y se demostró que los mejores resultados eran obtenidos por las metaheurísticas Record-to-Record Travel (RRT) y Escalador de Colinas. Los calendarios obtenidos ahorran entre un 13 y un 29 % de la distancia y se obtienen en menos del 1 % del tiempo, en comparación con la solución manual.
Palabras claves: metaheurísticas, problema de optimización combinatoria, problema de la transportación en un torneo, calendario deportivo.
ABSTRACT
The transportation cost of Baseball National Series includes the displacements of the team form one province to other. The total amount of traveled distance depends on the shedulle that defines the order of the games. Until 2012, theses schedules were constructed manually. The main goal of this paper is to demonstate how it can be reduced the total distance traveled by the teams by using metaheuristics. It was necessary to define the different aspects of the corresponding optimization problem. Then, several metaheuristics were compared in order to demonstrate that the best results were obtained by Record-to-Record Travel (RRT) and Hill Climbing. The schedules obtained by these metaheuristics allow to save between 13 and 29% of the overall distance travelled by teams and they are obtained in about 1 % of the time, in comparison to the official schedules designed by human experts.
Key words: metaheuristics, combinatorial optimization problem, traveling tournament problem, sport timetabling.
INTRODUCCIÓN
En los años recientes se han intensificado las investigaciones enfocadas al mejor uso de los portadores energéticos, con la introducción de nuevas tecnologías para disminuir su consumo. Esto es muy importante para reducir la contaminación ambiental y mejorar la eficiencia de las organizaciones. En el uso del combustible para la transportación hay otra dimensión a considerar: la reducción de la distancia total recorrida.En la Serie Nacional de Béisbol (SNB) de Cuba, que es el evento deportivo más importante y complejo del deporte cubano, la ubicación de los enfrentamientos entre los equipos en las distintas fechas del evento influye significativamente en la distancia total recorrida. Este complejo problema de optimización recibe el nombre de Problema de la Transportación en un Torneo (Travelling TournamentProblem, TTP). Ha recibido mucha atención en el mundo y ha sido enfrentado usando metaheurísticas. Hay muchas variantes del problema que hace difícil la creación de algoritmos heurísticos exactos para cada variante.
Las metaheurísticas son algoritmos de optimización de propósito general que buscan el mejor (mayor o menor) valor posible de la función a optimizar (llamada función objetivo) dentro del dominio del problema. Las metaheurísticas no exigen condiciones a la función a optimizar, ni a las variables que definen el problema. Esto diferencia a las metaheurísticas de los algoritmos heurísticos particulares. Entre las metaheurísticas más conocidas están los Algoritmos Evolutivos, el Recocido Simulado, etc. Las metaheurísticas no garantizan encontrar el valor óptimo de la función, pero obtienen soluciones buenas en diversas aplicaciones [1, 2].
Algunas metaheurísticas que se usarán en este trabajo se comentan a continuación y se indica el término en inglés correspondiente. Todas toman decisiones aleatoriasy devuelven la mejor solución evaluada durante la ejecución del algoritmo. Parten de una solución inicial, generalmente aleatoria. Luego analizan nuevas soluciones, sucesivamente, hasta que llegar a una cantidad de soluciones evaluadas. Muchas utilizan el principio de búsqueda local, donde las nuevas soluciones son obtenidas a partir de modificaciones de otras.
El Camino Aleatorio (Random Walk) parte de una solución dada y a partir de ahí le realiza una modificación que produce una solución nueva, que sirve de base para una nuevas modificaciones. A diferencia del Camino Aleatorio, el Escalador de Colinas (Hill Climbing), luego de modificar la solución actual y obtener una solución nueva, solo acepta la nueva como base para la próxima modificaciónsi es mejor, o igual, que la anterior. El Escalador de Colinas tiene el problema de quedarse estancado en óptimos locales, cuando todas las vecinas de la actual son peores. Para evitarlo, hay otras metaheurísticas que aceptan soluciones vecinas peores que la actual. La Aceptación por Umbral (Threshold Accepting) acepta soluciones peores, siempre que el valor del empeoramiento sea menor que un umbral. El Recocido Simulado (Simulated Annealing) acepta soluciones peores con una probabilidad que es inversamente proporcional al empeoramiento y directamente proporcional a un parámetro llamado temperatura, que va decreciendo. Esta metaheurística se inspira en el recocido o temple de los metales para garantizar que el material no quede en un estado frágil asociado a un mínimo local de energía. La forma usual de descender la temperatura es multiplicándola por un factor de reducción (valor entre 0 y 1), que es un parámetro de esta metaheurística. El algoritmo RRT (Record-to-Record Travel) acepta las soluciones nuevas si la diferencia de calidad entre la solución nueva y la mejor encontrada hasta ese momento es menor que un valor definido como parámetro. La metaheurística conocida como Algoritmo del Gran Diluvio (Great Deluge Algorithm) acepta las nuevas soluciones si ellas están por encima de un valor llamado nivel del agua. El nivel del agua parte de un valor que es un parámetro del algoritmo, y se va incrementando cada vez un valor, definido por un parámetro llamado lluvia.
Todas la metaheurísticas anteriores mantienen una sola solución de referencia para generar nuevas. Hay otra metaheurísticas, llamadas poblacionales, que mantienen varias soluciones y generan las nuevas soluciones a partir de esas. Las Estrategias Evolutivas (Evolution Strategies) comienzan con una población inicial de soluciones, generalmente aleatorias. Luego, se repite un ciclo en que se encogen las mejores de ellas, para luego ser usadas para generar una nueva población realizándole modificaciones a estas mejores, hasta llenar de nuevo una población completa. Con esta nueva población se repite el proceso. El tamaño de la población y la cantidad de soluciones que se escogen para generar la nueva población son parámetros.
Por la amplitud del tema, la explicación anterior no entra en detalles que pueden consultarse en [1, 2], donde también puede encontrarse una amplia variedad de aplicaciones. Es importante acotar que ninguna metaheurística es superior a otra, según el Teorema NFL (No Free Lunch) [3]. Para aplicar una metaheurística en un problema concreto deben definirse algunos aspectos como:
La representación de una solución, con las variables que definen el espacio de soluciones posibles.
La forma de construir soluciones del problema, generalmente de manera aleatoria o pseudoaleatoria.
Los operadores de mutación, que son la forma de modificar soluciones para obtener otras nuevas.
La forma de evaluar las soluciones del problema, es decir, la función objetivo.
El Problema de la Transportación en un Torneo se define por primera vez en [4] motivado por un estudio de los calendarios de las principales ligas deportivas de Estados Unidos, en particular la MLB (Major League Baseball). Luego se ha aplicado en competencias de diferentes deportes y países como el futbol de Brasil, el voleibol de Argentina, el futbol de Bélgica, el tenis, entre otras. El problema consiste en la definición de un calendario para n equipos, siendo n par, donde todos los equipos se enfrentan al menos una vez contra todos los demás equipos de la competencia. Un enfrentamiento entre dos equipos ocurre normalmente en la sede de uno de los dos equipos. Al equipo que juega en su sede se le llama "home club", y al otro, "visitador". El principal objetivo de este problema es reducir los recorridos de los equipos durante las competencias. Según la cantidad de vueltas completas a realizarse durante la competencia, los torneos se clasifican en [5-7]:
Un "todos contra todos" simple (en inglés: Simple Round Robin, SRR): Se realiza una sola vuelta completa.
Un "todos contra todos" doble (en inglés: Double Round Robin, DRR): Es una competencia donde cada equipo se enfrenta dos veces a los restantes, jugando una vez como home club y otra como visitador.
Se han propuestos variantes de cómo enfrentar el problema. Algunas de las más conocidas son:
Minimizar la distancia total, obtenida de sumar las distancias recorridas por cada equipo [4, 8].
Minimizar la distancia máxima recorrida por el equipo que tiene el recorrido más largo [5].
Minimizar la diferencia entre la distancia recorrida por los equipos con el recorrido mayor y el menor [9]
Se han definido otras variantes del problema, y en general se han considerado muchos aspectos relativos a las distribución de los juegos en cada vuelta [4, 5], la existencia de sedes predefinidas [10], otro elemento variable en la literatura es la cantidad de equipos [4, 11].
Para resolver estos problemas, las formas más empleadas para representar las soluciones expresan los enfrentamientos entre dos equipos, diferenciando quien es home club o visitador. Las más utilizadas son:
Una secuencia de fechas de enfrentamientos con los pares de equipos que jugará en esa fecha[12].
Una matriz donde las filas son los equipos y las columnas las vueltas simples. Para indicar que el equipo es home club, o visitador, se utiliza un signo positivo o negativo [10] ouna matriz auxiliar [13].
El espacio de soluciones del problema es explorado a través de varios operadores o mutaciones. Algunos de los operadores más comunes son [5]:
Intercambio de home club por visitador, en uno de los enfrentamientos.
Intercambio de equipos: se intercambian un equipo por otro en toda la planificación.
Inserción de juego: se elimina un juego de una vuelta y se inserta enotra, ajustando el resto del calendario.
Se han aplicado muchas metaheurísticas para resolver el problema como son: búsqueda tabú [9], recocido simulado [14], algoritmo genético [12, 15], búsqueda local iterada [10], entre otras.
Como se ha visto, el Problema de la Transportación en un Torneo ha recibido mucha atención en los últimos años. Al existir muchas variantes de él, es muy difícil extrapolar las soluciones reportadas a otro caso, ya que tienen cada una en cuenta diferentes diseños de calendarios o intereses a satisfacer. Estas variaciones del problema hacen que la selección de la metaheurística más conveniente para cada caso sea un problema abierto, lo cual queda reforzado por el Teorema No Free Lunch (NFL)[3].
En base a lo anterior, queda abierto el problema científico asociado a determinar si es posible optimizar los calendarios de las Series Nacionales de Beísbol usando algoritmos metaheurísticos. Para poder responder a esta pregunta es necesario hipotetizar sobre las posibilidad de definir todos los elementos necesarios para la solución del correspondiente problema de optimización mediante el uso de metaheurísticas, sujeto a las singularidades cubanas. Por tanto, las secciones siguientes se enfocan al objetivo de plantear los diferentes componentes que permitan la optimización de los calendarios usando metaheurísticas y a la identificación de las metaheurísticas que mejor comportamiento tengan en este problema.
En la sección siguiente se explican las particularidades de la Serie Nacional de Beisbol en Cuba, y en base a eso, se explica cómo se definen cada uno de los elementos necesarios para optimizar el calendario de estas usando metaheurísticas. Luego, se presentan los resultados experimentales de la comparación entre diferentes configuraciones de metaheurísticas, y la comparación con las soluciones obtenidas por expertos.
MATERIALES Y MÉTODOS
Un calendario
En Cuba, según la forma de competencia que se use, en cada Serie Nacional de Béisbol (SNB) se definen un conjunto de enfrentamientos que deben efectuarse entre los equipos que participen. Así, se entiende por enfrentamiento a la realización de tres juegos entre un par de equipos en el estadio de uno de ellos. Por
ejemplo, en la SNB 50 cada uno de los 16 equipos participantes se enfrentó dos veces con cada uno de los 15 restantes, una vez en su sede (home club), y otra vez en la sede del otro (visitador). Eso implica que cada equipo tenía que realizar 30 enfrentamientos. Para poder ejecutar todos los enfrentamientos, el calendario define 30 fechas para realizar esos 30 enfrentamientos de cada equipo. En cada una de las fechas se realizan varios enfrentamientos. Por ejemplo, en la SNB 50 en cada fecha se realizaron 8 enfrentamientos, que incluyen en total a los 16 equipos. En general, un calendario consiste en la asignación de cada uno de los enfrentamientos a cada una las fechas. Para cada equipo existen tantos calendarios como posibles asignaciones hay de sus enfrentamientos a las fechas. Por ejemplo, para uno de los equipos de SNB 50 hay 30! = 2.65*1032 calendarios posibles, dado por las posibles permutaciones (ordenamientos) de sus enfrentamientos en las fechas. Sin embargo, a la hora de conformar el calendario completo de la competencia debe tenerse en cuenta que en cada fecha un equipo solo puede efectuar un enfrentamiento.
Como se vio en la sección anterior, hay distintos tipos de calendarios. En la variante "todos contra todos" doble, la cantidad de fechas n está dada por la ecuación 1, donde t es la cantidad total de equipos.
Esa fue la variante usada en las SNB 50 y 51. No obstante, hubo una diferencia entre ambas SNB, pues la SNB 51 uso la variante de calendario reflejado y no fue así en la SNB 50. Por su parte, en la SNB 52, se empleó la variante "todos contra todos" simple, donde la cantidad de fechas n está dada por la ecuación 2.
Adicionalmente, hay otras singularidades en las SNB cubanas como las siguientes:
- Juego inaugural entre finalistas o no: En los últimos años se incorporó una novedad a las SNB que consiste en que se agrega una fecha extra al inicio del calendario normal, para realizar un juego que inaugura la SNB en que participan el equipo campeón y el subcampeón de la SNB anterior. En esa fecha solo se realiza ese juego. Luego, cuando según el calendario le corresponda el enfrentamiento entre esos equipos, el enfrentamiento solo incluye otros dos juegos, para completar los tres juegos de este.
- Se incluye o no descanso. Si la SNB incluye una cantidad impar de equipos, en cada fecha tiene que haber un equipo que descansa, es decir no juega en la fecha y el equipo regresa a su sede a descansar. Por ejemplo, la SNB 51 que incluyó t=17 equipos tuvo descanso. En las SNB 50 y 52 no lo hubo.
- Restricciones en los enfrentamientos seguidos como visitador: Comúnmente esta cantidad es de 4 enfrentamientos.
- Las dos primeras de estas singularidades no se han encontrado en la literatura consultada porque son características de la SNB de Cuba.
Representación
Para poder resolver el problema de optimizar el calendario de una SNB es necesario definir la forma en que se representa cada solución (calendario). En este trabajo, cada calendario C se representa como una vector de n dimensiones que son las fechas. La i-ésima fecha Fi es un conjunto con una cantidad de m enfrentamientos, donde el j-ésimo enfrentamiento de la fecha Fi, es decir el enfrentamiento Eij, es un par ordenado que incluye a los equipos que se enfrentan S y V, siendo S la sede y V el visitante. Formalmente se puede decir:

La ecuación 3 asegura que un equipo no aparezca dos veces en la misma fecha.
En cuanto a la cantidad de enfrentamientos m por cada fecha Fi, si t es par y no hay descansos se calcula con la ecuación 4, y si t es impar y, por tanto, hay descanso, se calcula con la ecuación 5.
Por ejemplo, un calendario para una hipotética SNB con Equipos={A,B,C,D} y calendario doble, usando las expresiones anteriores, quedaría t=4, n= 6 y m=2. Un calendario podría representarse como sigue:
Calendario 1=[{(A,B),(C,D)},{(A,C),(B,D)},{(D,A),(C,B)},{(B,A)(D,C)},{(C,A)(D,B)},{(A,D)(B,C)}]
Para facilitar la comprensión, en la tabla 1 se muestran ese y otros dos calendarios de esa hipotética SNB. Todos estos calendarios son dobles, restringidos, sin juego inaugural, ni descanso, ni otras restricciones. En cada enfrentamiento X-Y se entiende que el primero de ellos X es el equipo que juega como sede (o "home club") mientras que Y es el visitador. La tabla 2 muestra los itinerarios a recorrer por cada uno de los equipos para el Calendario 1 de la tabla 1.
Cuando la cantidad de equipos aumenta, aumentan también de manera notable las variantes de calendarios. En este ejemplo con 4 equipos, 6 fechas y con calendario doble con restricciones cada equipo tiene solo 3! = 6 variantes de itinerarios. En la SNB 50 con 16 equipos, 30 fechas y sin restricciones cada equipo tiene 30! = 2.65*1032 posibles itinerarios. Esto permite percibir la complejidad del proceso de optimizar un calendario para minimizar el costo de transportación entre sedes.
Costos asociados a un calendario
La ejecución de un calendario incluye distintos costos como los de alojamiento, iluminación de los estadios, etc. Este trabajo se concentra en uno de estos aspectos: el costo de transportación de los equipos entre las sedes. Puede observarse que muchos de los otros costos son fijos y no dependen del calendario. Sin embargo, el costo de transportación entre las sedes varía con el calendario, porque el itinerario de un equipo dependerá del enfrentamiento que corresponde a cada fecha.
En las SNB la transportación de los equipos se realiza en ómnibus, moviéndose cada equipo de la sede en que ocurra un enfrentamiento en una fecha dada a la sede del enfrentamiento de la fecha siguiente. Esto implica que el costo total de la transportación entre sedes está determinado por el itinerario que debe recorrer cada equipo para cumplir el calendario. El costo de transportación dependerá del costo del combustible empleado, del desgaste de los neumáticos, etc. Sin embargo, todo esto depende en esencia de la cantidad de kilómetros recorridos por todos los equipos. En la SNB 50 la distancia total recorrida entre todos los equipos fue de más de 100 mil kilómetros, y en la SNB 51 fue de más de 175 mil. Esta diferencia entre ambas estuvo marcada por dos aspectos importantes. En la SNB 51 hubo un equipo más, y además esto hizo que la cantidad de equipos fuera impar. Esto implicó que en cada fecha el equipo que descansaba tenía que regresar a su sede, y luego partir de ahí a la sede de su enfrentamiento en la fecha siguiente.
La figura muestra, gráficamente, las implicaciones de cada calendario en costo. Cada uno de ellos es un grafo donde los nodos representan las sedes de cada equipo, y al lado de cada arco que une las sedes se ha colocado una línea de un color dado por cada vez que el equipo identificado con ese color tiene que recorrerlo. La tabla 3 muestra los costos de transportación para ciertas distancias entre los puntos. Este ejemplo simple muestra las notables diferencias en costos asociados a los calendarios.

Para emplear las metaheurísticas para resolver este problema, hay que definir la forma de evaluar cada uno de los calendarios. En este caso, la evaluación incluirá los dos aspectos.
El primer aspecto a incluir en la evaluación es el total de kilómetros recorridos (KMT). Este consiste en la suma de los kilómetros recorridos por cada equipo como muestra la ecuación 6, donde la cantidad de kilómetros recorridos por cada equipo está dada por la suma de las distancias recorridas entre las sedes consecutivas en el itinerario, según se muestra en la ecuación 7, la ecuación 8 y la ecuación 9.
La función sede(e,i) devuelve la ciudad que es sede del enfrentamiento que corresponde al equipo e en la fecha i, que dependerá de si le corresponde ser sede o visitador en el enfrentamiento de esa fecha. Para calendarios con descansos, en cada fecha que un equipo descansa se considera equivalente a si jugara como sede, porque implica un regreso a su ciudad, y es la razón de la última condición de la función sede.
Debe notarse que KMe, que es el costo total en kilómetros recorridos por el equipo e, suma también el costo inicial del movimiento de la sede del equipo e a la sede del enfrentamiento en la primera fecha, así como el movimiento final de regreso luego de la última fecha. Cuando hay semanas de descanso general para todos los equipos (por ejemplo en fin de año), en esas fechas los equipos regresan a su sede, lo cual se incluye también en el itinerario, y consecuentemente en los costos de transportación.
La función distancia (X,Y) calcula la distancia entre dos ciudades, y se asume como entrada.
El otro aspecto a incluir en la evaluación es el incumplimiento de la restricción de encuentros seguidos como visitador (IEV), que se muestra en la ecuación 10. Aunque un calendario sea correcto, puede ocurrir que aparezca en él un equipo que tenga una cantidad de enfrentamientos seguidos como visitador que exceda una cantidad fijada por criterios de diseño. Esto se hace para evitar largos períodos fuera de su sede de cada equipo.
IEVe cuenta la veces que un equipo e en el itinerario juega más de V juegos como visitador de manera consecutiva. Por ejemplo, Itinerario de A que aparece en la tabla 2 que es A,A,D,B,C,A si V=2 habría un incumplimiento porque se incluye la secuencia de fechas D,B,C en que A es visitador. Esto hace que IEVA=1. Puede notarse en la misma tabla que en los demás equipos se cumple la restricción para V=2, por lo que el único incumplimiento es con el equipo A, quedando finalmente IEV=1. En las SNB se trabaja normalmente con V=4, lográndose calendarios que generalmente respeten esto, como en la SNB 50. Sin embargo, en la SNB 51 se incumplió esta restricción una vez (IEV=1), porque una vez el equipo Villa Clara tuvo 5 enfrentamientos seguidos como visitador.
Para combinar ambos aspectos en la función objetivo se usará una suma ponderada de ambos aspectos, quedando como aparece en la ecuación 11.
En esta función objetivo FO, P es un valor para penalizar los calendarios que incumplan con la restricción de diseño. El valor de penalización es importante para las metaheurísticas. Si P es pequeño, el algoritmo podría devolver soluciones que violen las restricciones pero que tiene buenos valores en otros aspectos. Para garantizar que no se violen las restricciones se usa un valor grande para P. En este caso se usa P=1 000 000, que garantiza que los calendarios son mejores mientras menos incumplan las restricciones. Dentro de los que tengan un incumplimiento IEV igual, son preferibles las de menos kilómetros recorridos KMT. Puede notarse que FO es siempre negativa, porque lo ideal es que KMT y IEV tengan el menor valor posible. En este trabajo se enfocará la metaheurística a maximizar esta función negativa, lo cual es equivalente a minimizar la función positiva opuesta.
Construcción
Para construir un calendario inicial correcto, deben ubicarse todos los enfrentamientos posibles en las fechas, sin tener en cuenta el valor de la función objetivo.
El conjunto de enfrentamientos es TE= {(x,y)|x≠y, x,y∈Equipos}, para el caso general de un calendario doble. En ese caso, w es el total de enfrentamientos (cardinalidad de TE) y queda como muestra la ecuación 12. Para el calendario hipotético con t= 4 de la tabla 2 se cumple w= 12.
En el caso del calendario simple, como se juega un solo enfrentamiento entre cada par de equipos entonces se calcula como aparece en la ecuación 13.
En este caso, w solo cuenta las combinaciones de posibles parejas, sin diferenciar entre quien está en cada rol pues entre cada par de equipos hay un solo juego. En estos calendarios con un solo enfrentamiento entre cada par de equipos, es la dirección de la SNB la que decide donde se jugará cada enfrentamiento.
En cualquier caso, el algoritmo de construcción de un calendario debe recibir una lista de enfrentamientos TE y debe producir un calendario. Este consiste en la asignación de los enfrentamientos a las fechas, cumpliendo las condiciones que lo hacen ser un calendario correcto, es decir que este cumpla con la condición de que no se repita un equipo en cada fecha, y que se ubiquen todos los juegos posibles. En este punto, no se tiene en cuenta el costo del calendario, ni ninguna otra restricción.
Para lograrlo se implementó un algoritmo de construcción que parte de un calendario inicial vacío (sin enfrentamientos por fecha) y de una lista de enfrentamientos por asignar EPA (que contiene a cada uno de los enfrentamiento de TE). El algoritmo va formando el calendario incrementalmente, agregando cada vez un nuevo enfrentamiento a una fecha, garantizando que este enfrentamiento no contenga (ni como sede, ni como visitador) a un equipo que ya esté contenido (como sede o como visitador) en los juegos anteriormente asignados a esa fecha. Cada vez que se agrega un enfrentamiento a una fecha, este se elimina de EPA.
En cada momento puede existir más de un juego potencialmente asignable a una fecha, comenzando por la situación trivial inicial en que no haya aún enfrentamientos en una fecha, y que por tanto cualquier enfrentamiento puede ser asignado. Para decidir cuál de los enfrentamientos posibles se asigna a la fecha, el algoritmo los toma en el orden en que aparecen en EPA. Esto implica que este algoritmo de construcción produce diferentes calendarios según el orden de los enfrentamientos de TE dentro de EPA. En este trabajo se experimentará con un orden fijo de occidente a oriente, donde los enfrentamientos en EPA aparecen ordenados según el orden de occidente a oriente de los equipos, ordenando primero por la sede y dentro de los de igual sede por el visitador.
Modificación
Una vez definida la representación y la forma en que se construye la solución inicial, para utilizar una metaheurística deben definirse operadores que modifican una solución dada para generar una nueva solución que sea una variación de ella. A estos operadores se les llama comúnmente operadores de mutación o simplemente mutaciones. Aquí, como se parte de un calendario construido correctamente, los operadores de mutación deben garantizar que las nuevas soluciones generadas sigan siendo correctas. Las mutaciones que se emplearán en este caso son las siguientes:
Cada una de estas mutaciones es realmente una familia de mutaciones, porque los parámetros concretos de cada una de ellas se generan aleatoriamente. Por ejemplo, M6 incluye el intercambio de cualquier par de fechas, y por tanto incluye realmente t(t-1) variantes de pares de fechas a intercambiar. Para el ejemplo hipotético de 4 equipos y 6 fechas habría 30 variantes de M6, por ejemplo intercambiar 2 y 5, o intercambiar 4 y 6. Lo mismo ocurre en las demás, con las posibilidades de variar los equipos en M1 y M4, o el enfrentamiento en M3. En la tabla 4 aparecen ejemplos de las mutaciones anteriores. Como los calendarios deben seguir siendo correctos después de aplicarse las mutaciones, cuando se realiza una mutación como M2 y M3 que modifica el equipo que es sede en una fecha dada también deben cambiarse los otros enfrentamientos entre ese par de equipos. Es curioso notar que la M7 produce en este caso lo mismo que si se hubiera intercambiado las fechas 1 y 2. Esto pasa porque para lograr que las fechas sigan siendo correctas y se mantengan las sedes hubo que cambiar todos los juegos. Solo para ejemplificar mejor esta mutación M7 se agrega el ejemplo siguiente con un calendario con más encuentros por sede que permite mostrar lo que ocurre. Suponga un calendario {…,Fx,…,Fy,…} con 8 equipos (A,B,C,D,E,F,G, y H), donde los puntos suspensivos representan fechas del calendario que no se modificarán y siendo:

Puede notarse que los cambios solo afectaron a los equipos involucrados en los enfrentamientos que serán intercambiados, y no a la fecha completa.
A partir de lo anterior puede verse que hay ciertas mutaciones que modifican las sedes de los enfrentamientos, que son M1, M2, M3 y M4. Como en las SNB que tienen calendarios simples debe respetarse las sedes prefijadas, entonces para obtener los calendarios de estas SNB solo se emplean las mutaciones M0, M5, M6 y M7, por ejemplo en la SNB 52. En las demás, todas las mutaciones están disponibles, y se selecciona en cada paso la mutación a usar de manera aleatoria.
Casos de estudio
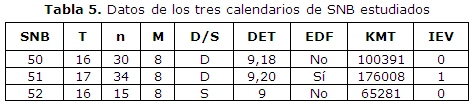
Para estudiar el comportamiento de las metaheurísticas en el problema, se estudiaron tres casos de calendarios de SNB, que son los correspondientes a las últimas y que además tienen suficiente diferencia entre ellos. La tabla 5 resume estas diferencias, manteniendo la nomenclatura donde t es la cantidad de equipos, n es la cantidad de fechas, m es la cantidad de encuentros por fecha. Las demás columnas indican si el calendario fue doble (D) o simple (S), si incluyó descansos antes de determinadas fechas (DET), si hubo equipos que descansaban en cada fecha (EDF).
En todas hubo juego inaugural entre el campeón y subcampeón de la SNB anterior. Adicionalmente debe decirse que aunque las SNB 50 y 52 tienen el mismo total de equipos (t=16), hay 14 de ellos que son iguales, pero hay dos diferentes. Las columnas KMT y la columna IEV se corresponden con los dos aspectos considerados en la evaluación de los calendarios: total de kilómetros recorridos, e incumplimiento de la restricción de juegos seguidos como visitador. La evaluación de estos aspectos se realizó sobre los calendarios oficiales de ambas SNB. Se incluyen como referencia respecto a los resultados que se mostrarán más adelante obtenidos por las metaheurísticas. En los casos de las SNB 50 y 51 los calendarios fueron creados manualmente por expertos de la Comisión Nacional de Béisbol que llevan años realizando esta tarea, para la cual emplean varias semanas. En el caso de la SNB 52, el calendario que se refiere es el correspondiente a la primera etapa. Este calendario fue realizado de una manera semiautomática, partiendo de una versión preliminar de esta propuesta con modificaciones hechas por los expertos manualmente.
Metaheurísticas a comparar
Según el Teorema NFL [3], no existe una metaheurística que sea superior a las demás en la totalidad de problemas. Esto lleva a la necesidad de experimentar con varias metaheurísticas para poder saber cuál se comporta mejor en el problema de interés. En este trabajo se compararán varias metaheurísticas, usando los parámetros mostrados en la tabla 6, dando lugar a diferentes configuraciones de metaheurísticas a ser comparadas. Se ha preferido mantener los nombres identificadores por sus siglas en inglés por ser más conocidos, y para cada caso se indica el nombre en inglés y su traducción al español.
Cada una de las variantes de configuración de parámetros de metaheurísticas de la tabla 6 partieron de criterios recomendados para cada una de ellas [1, 2], y se probaron ajustes de los mismos hasta llegar a los valores mostrados.
Criterios para analizar y comparar la calidad de los resultados
Para hacer justa la comparación de estas configuraciones, debe fijarse una cantidad igual de evaluaciones de la función objetivo. En este caso, este valor se fijó en 10 mil, debido a que luego de esta cantidad ninguna de las configuraciones mostró mejorías significativas.
En todos los casos, se realizaron 30 repeticiones debido a que las 11 configuraciones tienen un comportamiento estocástico, no devolviendo siempre el mismo resultado. De cada repetición de una configuración se obtuvo el máximo valor de la función objetivo, entre las 10 mil soluciones evaluadas.
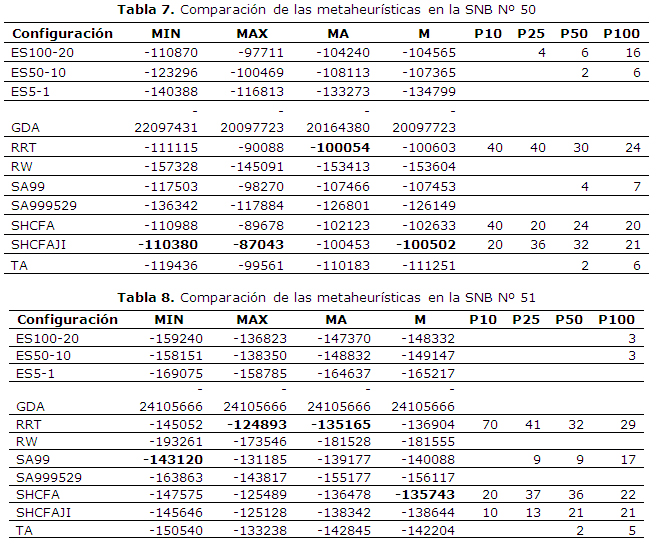
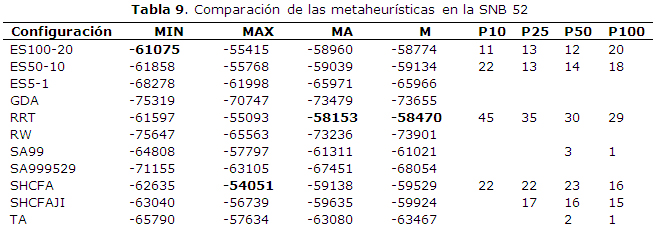
Para integrar y comparar los resultados de cada una de las configuraciones, se usaron cuatro medidas estadísticas para integrar los resultados de las 30 repeticiones de cada una de ellas: media aritmética, mediana, mínimo y máximo. Las columnas MA, M, MIN y MAX en las tablas 7, 8 y 9 se corresponden a estas medidas, respectivamente.
También se unieron las 30*11=330 soluciones mejores encontradas en cada una de las 30 repeticiones de las 11 configuraciones y se ordenaron, dándole un valor de rango a cada una, obteniendo el valor de rango 1 la mejor (máximo) y de 330 la peor (mínimo). Analizando el rango de las soluciones generadas por cada metaheurística permitirá saber la tendencia a obtener soluciones mejores, en adición a las medidas de tendencia central y extrema de cada configuración. Las columnas P10, P25, P50 y P100 en las tablas 7, 8 y 9 se corresponden con el porciento de las 10, 25, 50 y 100 mejores soluciones que son obtenidas usando cada configuración. Adicionalmente, se compararon las configuraciones usando la prueba de la suma de rangos de Wilcoxon con una significación de 0.005, tomando como poblaciones a comparar las 30 repeticiones de cada una. Esto sigue la recomendación dada en [16] de usar pruebas no paramétricas para comparar metaheurísticas.
RESULTADOS
DISCUSIÓN
Puede verse que el comportamiento de las distintas configuraciones es muy similar en las tres SNB analizadas, pudiendo agruparse las configuraciones según la calidad de los resultados de cada una.
- Ganadores: RRT, SHCFA, SHCFAJI. Estas tres configuraciones superan a las demás en la mayoría de los criterios y casos. RRT es la que generalmente obtiene los mejores resultados en las distintas medidas, siendo siempre superior a todas las metaheurísticas de los demás grupos usando la prueba de Wilcoxon, lo cual ocurre también generalmente para SHCFA y SHCFAJI. Usando la prueba de Wilcoxon no se obtuvo diferencia significativa entre las tres metaheheurísticas de este grupo. Debe notarse que estas metaheurísticas fueron las que obtuvieron la mejor solución para cada SNB aunque las dos del grupo quedaron cerca. RRT parece tener ligera ventaja en general, a pesar de no poderse establecer una superioridad estadísticamente significativa, por lo que se consideran ganadoras a las tres.
- Perdedores: RW, GDA. Estas metaheurísticas son superadas de forma general por las otras. En el caso de RW este resultado es común, debido que usan muy poco la información anterior para guiar la búsqueda. Para GDA este resultado es inesperado, y se deben a la dificultad para parametrizar esta metaheurística en este caso, llegando a obtener soluciones no factibles para dos SNB (valores por encima de 1000000).
- Medios: Las otras seis configuraciones (basadas en Recocido Simulado, Aceptación por Umbral y Estrategias Evolutivas) tienen un comportamiento intermedio, superándose indistintamente entre ellas, y quedando generalmente superadas por las metaheurísticas del grupo de los Ganadores y superando a las del grupo de los Perdedores. Puede destacarse en este grupo, que las configuraciones ES100-20 y SA99 quedaron cerca del grupo de los ganadores en algunos indicadores.
Finalmente la tabla 10 muestra una comparación de los resultados obtenidos en comparación con los calendarios obtenidos de forma manual por los expertos de la Comisión Nacional de Béisbol y que fueron las que se usaron como calendarios oficiales en las tres SNB. Para construir los calendarios de las SNB 50 y 51, los expertos emplearon varias semanas. En el caso de la SNB 52 se empleó como base una variante previa de esta propuesta que luego fue modificada manualmente por los expertos.
La columna KMT(O) muestra el total de kilómetros en el Calendario Oficial obtenido manualmente, mostrado en la tabla 5. La columna KMT(M) muestra el total de kilómetros de la solución mejor que fue encontrada con metaheurísticas, según lo mostrado en las tablas 7, 8 y 9. La columna Ahorro muestra la diferencia entre KMT(O) y KMT(M), y a la derecha el porciento del ahorro respecto a KMT(O). La columna CS muestra cuántas configuraciones de las 11 empleadas superan KMT(O) en cada SNB, y a su derecha el porciento que representa respecto a 11.
En la tabla 10 pueden verse los notables ahorros en kilómetros que pueden obtenerse con la propuesta, especialmente en las SNB 51 y 52. Estas SNB, al tener variaciones en la forma de su calendario respecto a las SNB anteriores, los expertos pudieron emplear menos su experiencia pues se enfrentaban a la tarea de construir calendarios a los que no estaban acostumbrados. Igualmente es significativo que para la SNB 50 se haya obtenido un ahorro de más del 10% a pesar de que para construirlo los expertos pudieron emplear en él todo el conocimiento de años anteriores, pues la forma general del calendario hasta esa SNB se había usado por más de 10 años. Es notable que 6 de las 11 configuraciones sean mejores que este calendario oficial de la SNB 50. Estas configuraciones fueron RRT, SHCFA, SHCFAJI, ES100-20, SA99 y TA, para un 55 % de lasconfiguraciones. En el caso de las SNB 51 y 52 la inmensa mayoría de las configuraciones logran superar la calidad del calendario oficial. Este resultado demuestra la conveniencia de enfocar la solución de este problema con metaheurísticas, más allá incluso de la metaheurística particular que se emplee. En el caso de la SNB 51 incluso ocurrió un incumplimiento de la restricción de que ningún equipo tuviera más de 4 enfrentamientos seguidos como visitador. Por tanto, para este caso, los calendarios encontrados en este trabajo superaran también al calendario oficial en este aspecto.
En general estos resultados muestran que las metaheurísticas constituyen una alternativa conveniente para reducir el costo de transportación en este tipo de problemas, incluso en los casos en que los expertos humanos hayan acumulado una notable experiencia resolviendo este tipo de problemas.
Otro aspecto destacable es que la solución propuesta mejora el tiempo para obtener los calendarios, que no excede los 5 minutos en una computadora de prestaciones básicas (procesador Pentium, 1.73 GHz de velocidad, 1 Gb de memoria RAM). Este tiempo es ínfimo comparado con las dos o tres semanas que le lleva normalmente a los expertos la construcción de un calendario. Como referencia puede notarse que 5 minutos constituyen el 0.2 % del tiempo de una semana de trabajo de 8 horas.
En el caso de la SNB 52 el calendario oficial de la primera etapa se construyó a partir de una versión preliminar de este trabajo, usando metaheurísticas. Ese hecho implica una aceptación por los expertos del valor de la propuesta. Adicionalmente, el tiempo corto para obtener los calendarios usando metaheurísticas tuvo un gran valor en este caso, debido al poco tiempo que medió entre que se decidió la estructura que iba a tener el calendario y la oficialización de este, que hubiera hecho muy compleja la elaboración totalmente manual en tan poco tiempo, o que hubiera implicado la obtención de un calendario peor. Posteriormente, se han construido calendarios usando los resultados presentados en este trabajo para la segunda etapa de la SNB 52.
CONCLUSIONES
Este trabajo enfoca el problema de la reducción del costo de transportación de las Series Nacionales de Beísbol desde la perspectiva de la optimización de los calendarios usando metaheurísticas. Se definió como objetivo de la optimización la reducción de la distancia total recorrida por los equipos en el torneo. A partir de un estudio experimental, se pudo demostrar que las metaheurísticas que mejores resultados obtuvieron fueron Record-to-Record Travel (RRT) y Escalador de Colinas.
Debido a la complejidad de este problema de optimización y la gran cantidad de soluciones posibles, no es posible saber si las soluciones obtenidas son óptimas. Sin embargo, se pudo comprobar que los calendarios obtenidos con las metaheurísticas permiten un ahorro que está entre el 13 % y el 29 % del total de kilómetros recorridos, en comparación con las construidas manualmente por los expertos humanos. También se comprobó que las metaheurísticas obtienen los calendarios en tiempos inferiores a los 5 minutos, lo cual implica menos del 1 %, respecto a las dos o tres semanas que debe emplear un experto humano para construirlo manualmente.
Los resultados presentados en este trabajo han sido aplicados en la elaboración de los calendarios que se han empleado en los dos últimos campeonatos cubanos.
AGRADECIMIENTOS
Los autores desean agradecer el apoyo y la colaboración recibida de la Comisión Nacional de Béisbol para la realización de este trabajo, especialmente a los expertos Ybrahim Averoff y Carlos del Pino. Igualmente, ha sido muy valioso el trabajo de los revisores de este trabajo que han ayudado a mejorarlo.
REFERENCIAS
1. Doerner, K. F., Gendreau, M., Greistorfer, P., et al. "Metaheuristics: Progress in Complex Systems Optimization". En: Operations Research/Computer Science Interfaces Series, New York: Springer Science and Business Media, 2007, 409 p. p. 153-167. ISBN 978-0-387-71921-4. DOI 10.1007/978-0-387-71921-4.
2. Talbi, E. Metaheuristics: From Design to Implementation. New Jersey: John Wiley & Sons. 2009, 618p. p. 1-79. ISBN 978-0-470-27858-1.
3. Wolpert, D. H. y Macready, W. G. "No Free Lunch Theorems for Optimization". IEEE Transactions on Evolutionary Computation. 1997, vol. 1, nº 1, p. 67-82. ISSN 1089-778X. DOI 10.1109/4235.585893.
4. Easton, K., Nemhauser, G. y Trick, M. "The Traveling Tournament Problem Description and Benchmarks". En: Principles and Practice of Constraint Programming. 2001, p. 580-584. ISBN 978-3-540-45578-3. DOI 10.1007/3-540-45578-7_43.
5. Ribeiro, C. C. y Urrutia, S. "Heuristics for the Mirrored Traveling Tournament Problem". European Journal of Operational Research. 2007, vol. 179, nº. 3, p. 775-787. ISSN 0377-2217. DOI 10.1016/j.bbr.2011.03.031.
6. Kendall, G., McCollum, B. y Cruz, F. "Scheduling English Football Fixtures: Consideration of Two Conflicting Objectives". En: 8th International Conference on Practice and Theory of Automated Timetabling, PATAT, Belfast, UK: Queen's University, 2010, p. 1-15. ISBN 08-538-9973-3.
7. Imahori, S., Matsui, T. y Miyashiro, R. "An Approximation Algorithm for the Unconstrained Traveling Tournament Problem". En: 8th International Conference on Practice and Theory of Automated Timetabling. Belfast, UK: Queen's University. 2010, p. 508-512. ISBN 08-538-9973-3.
8. Bar-Noy, A. y Moody, D. "A Tiling Approach for Fast Implementation of Traveling Tournament Problem". En: 6th International Conference on Practice and Theory of Automated Timetabling. Brno, The Czech Republic: Faculty of Informatics, Masaryk University. 2006, p. 352-358. ISBN 80-210-3726-1.
9. Bonomo, F., Burzyn, A., Cardemil, A., et al. "An application of the traveling tournament problem: The Argentine volleyball league". Interfaces. 2012, vol. 42, nº 3, p. 245-259. ISSN 0092-2102. DOI 10.1287/inte.1110.0587
10. Costa, F. N., Urrutia, S. y Ribeiro, C. C. "An ILS heuristic for the traveling tournament problem with predefined venues". Annals of Operations Research. 2012, vol. 194, nº 1, p. 137-150. ISSN 1572-9338. DOI 10.1007/s10479-010-0719-9
11. Ribeiro, C. C. y Urrutia, S. "Scheduling the Brazilian Soccer Championship". En: 6th International Conference on Practice and Theory of Automated Timetabling PATAT. Brno, The Czech Republic: Faculty of Informatics, Masaryk University. 2006, p. 481-483. ISBN 80-210-3726-1
12. Choubey, N. S. "A Novel Encoding Scheme for Traveling Tournament Problem using Genetic Algorithm". En: IJCA Special Issue on Evolutionary Computation. 2010, vol. 2, p. 79-82. ISBN 978-93-80747-03-7. DOI 10.5120/1536-139
13. Suzuka, A., Miyashiro, R., Yoshise, A. et al. "Semidefinite programming based approaches to home-away assignment problems in sports scheduling," En: Algorithmic Applications in Management. Lecture Notes in Computer Science. Berlin: Springer Berlin Heidelberg, 2005, p. 95-103. ISBN 978-3-540-32440-9. DOI 10.1007/11496199_12.
14. Kendall, G., McCollum, B., Cruz, F. R. et al. "Scheduling English football fixtures: consideration of two conflicting objectives". En: Hybrid Metaheuristics. Berlin: Springer Berlin Heidelberg, 2013. p. 369-385. ISBN 978-3-642-30671-6. DOI 10.1007/978-3-642-30671-6_14
15. Schonberger, J., Mattfeld, D. C. y Kopfer, H. "Automated Timetable Generation for Rounds of a Table-Tennis League". En: Evolutionary Computation. La Jolla, CA, 2000. p. 277-284. ISBN 0-7803-6375-2
Recibido: 19 de abril de 2013.
Aceptado: 12 de junio de 2013.
Alejandro Rosete-Suárez. Instituto Superior Politécnico José Antonio Echeverría. Facultad de Ingeniería Informática. La Habana. Cuba
Correo electrónico: rosete@ceis.cujae.edu.cu