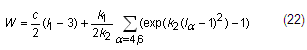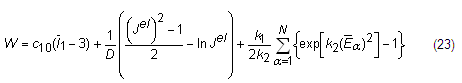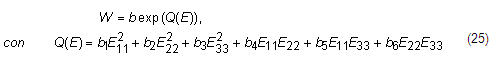Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Mecánica
versión On-line ISSN 1815-5944
Ingeniería Mecánica vol.17 no.3 La Habana sep.-dic. 2014
ARTÍCULO DE REVISIÓN
Modelos constitutivos para paredes arteriales, descripción del movimiento y estado de deformación
Constitutive models for arterial walls, description of movement and state of deformation
Diana Otero-Martínez, Luís-L. Otero-Pereiro
Instituto Superior Politécnico José Antonio Echeverría, Facultad de Ingeniería Mecánica. La Habana, Cuba
RESUMEN
Las paredes arteriales son uno de los tejidos blandos encontrados en los seres vivos. Tienen como características ser no lineales, incompresibles y anisotrópicos. En los últimos años se han desarrollado un conjunto de modelos constitutivos que consideran un material hiperelástico. Algunos de estos modelos consideran isotropía del material pero han demostrado no ser adecuados para modelar el comportamiento de arterias sanas. Los modelos más difundidos en este sentido consideran el material anisotrópico debido a la organización de las fibras de colágeno y a pesar de haber sido formulados para describir la conducta arterial pueden ser utilizados para representar el comportamiento de otros tejidos blandos como la vena cava infra-renal, la pared intestinal, las propiedades mecánicas del esófago, entre otros. Algunos autores incluso los han utilizado para modelar también el daño en las arterias.
Palabras claves: modelo constitutivo, tejido arterial, elasticidad, pared aortica, análisis de tensiones, respuesta pasiva.
ABSTRACT
Arterial walls are one of the soft tissues found in living organism. They are non lineal, incompressible and anisotropic. A set of constitutive models have been developed considering a hyperelastic material. Some of these models consider material isotropy but they have proved to be inadequate for modeling healthy arterial behavior. Mostly used models consider the anisotropic material due to the collagens fibers and nevertheless they have been created to describe arterial behavior can be also used for modeling different soft tissue behavior as infrarenal vena cava, intestine wall, mechanical properties of the esophagus, among others. General author have used them for modeling arterial damage.
Keywords: constitutive modelling, arterial tissue, elasticity, aortic wall, stress analysis, passive response.
INTRODUCCIÓN
Los tejidos blandos, cuando son sometidos a cargas, presentan grandes cambios de forma y una respuesta fuertemente no lineal. Una vez retiradas las cargas, retornan a posiciones muy cercanas a la inicial. Por otra parte, cuando son sometidos a cargas cíclicas exhiben en la respuesta una considerable disipación de energía. Los modelos utilizados en este tipo de materiales, destinados a simular su comportamiento, deberán ser capaces de captar todos estos fenómenos.
En general, los tejidos blandos son casi-incompresibles, no lineales y anisotrópicos. La teoría para la deformación finita de los materiales anisotrópicos incompresibles sobre la base de los invariantes de la deformación de Cauchy, fue desarrollada por Spencer [34]. Fung desarrolló un modelo para tejido suave basado en los componentes selectos de la deformación de Green [11]. Holzapfel ha descrito la implementación en elementos finitos de un modelo de Fung para las membranas biológicas [13, 14]
Aunque el comportamiento del material de la pared arterial es altamente anisotrópico debido a la organización de las fibras de colágeno, existen numerosos modelos usados en la literatura para describir el comportamiento de las arterias que consideran un comportamiento isotrópico. Entre ellos tenemos el modelo usado por Hoppmann [18], que no representa de manera adecuada el efecto de la rigidez en las arterias sometidas a grandes deformaciones. Encontramos también el modelo usado por Delfino et al [8] que presenta una función de energía potencial, parecida al comportamiento de la goma y es capaz de simular el efecto de la rigidez. Otros modelos consideran la anisotropía y utilizan funciones de densidad de energía de la deformación en los que consideran dos o tres familias de fibras de colágeno [11, 13, 14]. Los modelos más aceptados en este caso son el modelo de Holzapfel y el modelo de Fung. El modelo isotrópico de Demiray es adecuado para simular comportamientos de arterias con determinadas patologías como el síndrome de Marfan [12] o el comportamiento de la placa ateromatosa [33]. Sin embargo, para arterias sanas no describe adecuadamente su comportamiento mientras que el modelo de Holzapfel tiene una respuesta cercana a la experimental [28].
El comportamiento mecánico de la pared arterial está regido por la activación o no de las células del músculo liso vascular. La respuesta activa está gobernada por las propiedades de la elastina, el colágeno y el grado de activación de las células del músculo liso. Rachev y Hayashi [29] propusieron un modelo adecuado para describir este comportamiento. Sin embargo, la mayoría de los trabajos realizados en los últimos años están enfocados a describir la respuesta pasiva [17]. La poca cantidad de tejido muscular respecto a la presencia de elastina y colágeno hacen que el comportamiento de algunas arterias como la aorta sea fundamentalmente elástico y por la misma razón débilmente activa. La respuesta pasiva está gobernada por las propiedades de la elastina y el colágeno, en este comportamiento no se conoce bien cuál es la contribución de las células del músculo liso. Algunos autores han analizado por separado el papel de estos dos componentes en las propiedades arteriales [30, 32, 36]. La mayoría de los modelos de función de densidad de energía libre de la deformación propuestos en la literatura y que analizaremos en este trabajo, se usan para describir el comportamiento pasivo de la pared arterial [11, 13, 14].
En algunos programas como ABAQUS se han implementado modelos de comportamiento para tejidos blandos. En ese caso encontramos el modelo de Holzapfel [13, 14] que considera anisotropía con dos familias de fibras y el modelo de Fung [11] que considera tres familias de fibras. También el modelo de daño de Famaey et al [9, 10].
DESCRIPCIÓN DEL MOVIMIENTO. ESTADO DE DEFORMACIONES
En primera instancia se hace imprescindible un conocimiento exacto de los fenómenos de la elasticidad, principalmente en lo referente a los estados deformacionales, ya que los métodos de cálculo por elementos finitos se basan en la manipulación matemática del concepto de rigidez, sobre las bases físicas que se pretenden simular y que intervienen en el comportamiento de los sistemas elásticos, bien sean lineales o no lineales y que representen cualquiera de las restantes condiciones que se han enumerado de diversos comportamientos elásticos.
Por estas razones y ya que en lo delante de emplearán muchos términos relacionados con este aspecto se cree necesario hacer un breve enfoque por los aspectos más importantes relacionados con los desplazamientos y las deformaciones, comenzando por los dos tipos de formulaciones que se pueden utilizar.
Formulación Lagrangiana y Euleriana
En la descripción del movimiento (o desplazamiento) y deformaciones (y por lo tanto para el cálculo de tensiones) de los cuerpos, es fundamental la elección de un sistema de referencia para describir el mismo. En el cálculo lineal no existe distinción entre la configuración inicial (no deformada) y la configuración temporal (o deformada) ya que las características geométricas y mecánicas son invariantes. Ésta es la característica fundamental que diferencia el cálculo lineal del no lineal.
El medio continuo puede ser descrito bajo grandes deformaciones, lo cual introduciría el termino de no linealidad geométrica para describir el comportamiento. Entonces se pueden utilizar diferentes formulaciones en dependencia de si sus variables de estado están referidas a la configuración actual deformada, configuración Euleriana, o en términos de la configuración de referencia sin deformar, configuración Lagrangiana. [23], figura 1
![]() Configuración Inicial
Configuración Inicial
![]() Configuración Deformada
Configuración Deformada
El vector desplazamiento, Pp, figura 1, vendrá dado por la ecuación 1
Si se conociesen los vectores posición X y x para cualquier instante, estaría perfectamente definido el movimiento del cuerpo. En Mecánica de Medios Continuos, se supone que estas funciones son continuas y biunívocas, por lo tanto, es posible escribir (ecuación 2):
O bien (ecuación 3):
Las componentes del vector u es posible escribirlas en función de la posición inicial:
Formulación Lagrangiana, ecuación 4
O de la posición temporal:
Formulación Euleriana, ecuación 5
Se podría decir que la formulación Lagrangiana se ocupa de lo que le sucede al sólido, mientras que la formulación Euleriana se ocupa de lo que le sucede a una zona del espacio. Cuando la deformación es pequeña estas dos configuraciones son cercanas y los tensores de tensión y de deformación son aproximados:
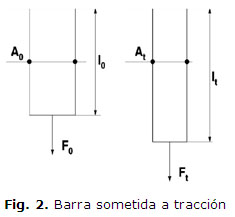
Si analizamos una barra sometida a tracción, figura 2, podemos ver como se relacionan los tensores de tensión de Cauchy, Lagrange y Kirchhoff.
Tensor de Cauchy: 
Tensor de Lagrange: ![]()
Tensor de Kirchhoff: ![]()
El tensor de Cauchy es la relación entre la fuerza y el área en la condición deformada. El tensor de Lagrange o Primer tensor de Piola-Kirchhoff relaciona la fuerza en la condición deformada con el área en la configuración de referencia. Mientras que el Segundo tensor de Piola-Kirchhoff relaciona la fuerza en la configuración de referencia con el área en la configuración de referencia.
Con respecto a la configuración Euleriana, las variables de estado a ser consideradas son la tensión de Cauchy y la deformación de Euler-Almansi [21, 23]. (ecuación 9)
Tensor de Almansi o tensor de deformación Euleriano.
Donde:
β es el tensor de deformación izquierdo de Cauchy - Green o también llamado tensor deformación de Finger, ecuación 10
V: Tensor alargamiento izquierdo
F: Tensor Gradiente de Deformación o matriz Jacobiana de la transformación.
Su determinante representa la relación de volúmenes entre la condición deformada e inicial . Transforma vectores en el entorno de un punto de la configuración de referencia a la configuración temporal, ecuación 12
Siendo: el Gradiente de desplazamiento
Respecto a la configuración Lagrangiana las variables son el segundo tensor de Piola-Kirchhoff S y la deformación de Green-Lagrange E, ecuación 13
Estos tensores están relacionados de la siguiente forma [4, 17], ecuación 14
W: función de densidad de energía libre de la deformación
C: es el tensor de deformación derecho de Cauchy - Green
U: Tensor alargamiento derecho
El Tensor Gradiente de Deformación no es un tensor simétrico, de ahí la definición de los tensores de deformación derecho e izquierdo de Cauchy - Green y , y del tensor de deformación Euleriano . Los tensores de deformación de Cauchy - Green dan medidas de la deformación del material independientes del sistema de referencia. Ambos tensores intervienen en la descripción de los materiales hiperelásticos que analizaremos a continuación.
HIPERELASTICIDAD
Algunos de los materiales elásticos empleados en la biomecánica son del tipo hiperelásticos. Estos materiales se encuentran caracterizados por la expresión de su función de densidad de energía libre de la deformación la cual describe como se almacena la energía en el cuerpo.
Para estos materiales tenemos el segundo tensor de tensiones de Piola-Kirchhoff S, que puede ser obtenido a partir de la función de densidad de energía libre de la deformación como se vio anteriormente (ecuación 13) y el tensor de Cauchy se relaciona con él de la siguiente manera: (ecuación 16)
Ambos pueden ser descompuestos en una parte que considera la contribución puramente volumétrica y la contribución isocórica. De esta misma forma se puede descomponer la función de densidad de energía libre de la deformación [6, 14]. Para los materiales hiperelásticos será una función de los invariantes de C (ecuación 17)
que se pueden obtener de la forma, ecuaciones 18
Generalmente las expresiones utilizadas para la función de energía libre de la deformación tienen forma exponencial [11, 14], las cuales pueden ser escritas de manera general como (ecuación 19):
Donde ![]() es la forma cuadrática de los componentes de deformación de Green-Lagrange [22].
es la forma cuadrática de los componentes de deformación de Green-Lagrange [22].
Las capas de las paredes arteriales se encuentran formadas por láminas con una única dirección preferente de las fibras de colágeno, lo que permitiría considerarlas como transversalmente isótropas. No obstante, se admite desde un punto de vista macroscópico que existen dos direcciones preferentes en cada capa. A partir de esta consideración se han desarrollado los modelos de anisotropía con dos y con tres familias de fibras de colágeno, aunque algunos autores han considerado modelos isótropos.
MODELOS ISÓTROPOS
Un modelo isótropo bastante aceptado para describir el comportamiento de la pared es el modelo de Demiray. Utilizado por Delfino y García Herrera [8, 12] y comparado con el modelo de Holzapfel [28], ecuación 20
Donde y son los parámetros del modelo e es el primer invariante del tensor derecho de Cauchy Green
Los resultados experimentales de los ensayos de tracción muestran que este modelo isótropo puede ajustarse adecuadamente al comportamiento de la pared en determinadas patologías como el síndrome de Marfan [12] o el comportamiento de la placa ateromatosa [33]. Sin embargo para arterias sanas no describe adecuadamente el comportamiento arterial mientras que el modelo de Holzapfel, que se verá a continuación, tiene una respuesta cercana a la experimental [28].
Anisotropía con dos familias de fibras
Para las arterias de gran tamaño, como la aorta y la carótida, la capa adventicia forma aproximadamente el 10 % del espesor de la pared [19] por lo que a veces se puede asumir que la capa media es la única con una respuesta mecánica significativa. El modelo más aceptado actualmente para describir la respuesta mecánica de la pared arterial es el comportamiento anisótropo de dos familias de fibras [24, 25, 27]. De acuerdo a esto se modela el tejido de una sola capa arterial reforzada por dos familias de fibras de colágeno, alineadas según dos direcciones preferentes [14, 15], aunque en algunos casos para arteria jóvenes y sanas se modelan las dos capas, con las especificaciones de cada capa por separado y se analiza el resultado del material compuesto [16, 20].
El material reforzado por las familias de fibras de colágeno, que son las responsables de la mayor parte de la respuesta mecánica de la pared, puede ser caracterizado por un número dado de direcciones preferentes no ortogonales. Estas fibras están orientadas formando un ángulo aproximadamente constante con la dirección axial del eje de la arteria, como se puede observar en la figura 3. [6, 12, 14]
Se considera un material con dos direcciones preferentes definidas en la configuración de referencia por dos vectores a0, b0 que forman ángulos simétricos con el eje del vaso ± φ La función de densidad de energía es ahora de la forma ![]() , debiendo verificarse, ecuación 21:
, debiendo verificarse, ecuación 21:
para todo tensor ortogonal R
Uno de los modelos propuestos para materiales biológicos con dos familias de fibras de colágeno, como son las paredes arteriales es el desarrollado por Holzapfel y Gasser [14]. La expresión de la función de densidad de energía de dicho modelo es, ecuación 22:
Este modelo propuesto por Holzapfel para describir el comportamiento de las arterias ha sido utilizado por diferentes autores para describir las propiedades de otros tejidos blandos. Entre ellos encontramos la vena cava infra renal ovina estudiado por Alastrue, et al [2] basado en este modelo pero con diferentes valores para los invariantes e , reproduciendo de manera adecuada el comportamiento del tejido. La pared intestinal fue modelada por Ciarletta, et al [7] teniendo en cuenta la contribución de las fibras musculares. Un modelo similar fue usado para describir las propiedades mecánicas del esófago por Yang, et al [38]. También fue usado por Zulliger, et al [40], para describir el alargamiento comprometido asociado con desrizo de las fibras de colágeno.
Este modelo ha sido utilizado también por algunos autores para describir el proceso de daño en la arteria. Famaey, et al [9] descompone la función de densidad de energía de la deformación en tres partes. Las dos primeras partes describen los componentes de la matriz del material con comportamiento anisotrópico y la contribución anisotrópica de las fibras de colágeno y se basa en el modelo de Holzapfel [14]. El tercer término caracteriza la anisotropía de las células del músculo liso y se basa en el modelo de Murtada, et al [26]. El daño acumulado en los diferentes componentes durante la carga mecánica es caracterizado por la función de daño de energía de la deformación para cada componente individual. Esta idea está basada en el estudio realizado por Balzani [6] para la formulación del daño. El modelo propuesto por Famaey ha sido implementado en ABAQUS donde se han realizado simulaciones para diferentes arterias con resultados bastante aceptables [10]. También ha sido utilizado para describir el crecimiento y remodelado vascular [3].
En ABAQUS se ha implementado anteriormente la función de densidad de energía de la deformación propuesta por Holzapfel en 2006 donde se agrega un tercer término al modelo anterior [13], ecuación 23:
Los dos primeros términos de la expresión representan la contribución volumétrica y distorsionar de la matriz del material no colagenoso con comportamiento isotrópico. El tercer término es la contribución de las fibras de colágeno teniendo en cuenta el efecto de la dispersión.
Donde, ecuación 24
Este término ![]() caracteriza la deformación de las fibras de colágeno con dirección preferente Aα
caracteriza la deformación de las fibras de colágeno con dirección preferente Aα
Las variables k, k1, k2, c10, D, son parámetros que dependen de la temperatura
N: es el número de familia de fibras .
![]() : primer invariante de la deformación
: primer invariante de la deformación
Jel: relación volumen elástico definido como expansión térmica
![]() : pseudo-invariantes de C y Aα
: pseudo-invariantes de C y Aα
Este modelo asume que cada familia de fibras de colágeno está dispersa con una dirección principal preferente. El parámetro describe el nivel de dispersión de las fibras. Debiendo encontrarse .
Holzapfel ha realizado estudios sobre la dispersión de las fibras de colágeno para lo cual propone un modelo modificado de ecuación 22 que tiene en cuenta un parámetro de dispersión [17]. A pesar de que en las arterias existe una alineación bastante fuerte de estas fibras, en otros casos como las válvulas cardiacas o en el miocardio, presentan una gran dispersión. Otros autores han realizado estudios sobre la contribución de la elastina y el colágeno en las propiedades de la pared arterial [1, 32, 37]. Rezakhaniha et al realizaron ensayos para determinar la orientación de las fibras de colágeno en la adventicia de la arteria carótida del conejo [31] y han llegado a la conclusión de existen cuatro familias de fibras de colágeno ya que se observan cuatro direcciones principales cuando la arteria se encuentra libre de cargas y las fibras de colágeno se mantienen en ondas. El modelo de Holzapfel asume que la elastina al igual que la matriz del material no colagenoso, tienen un comportamiento isotrópico, sin embargo algunos estudios realizados sugieren que en realidad el comportamiento de ambos es anisotrópico [30, 31, 37].
Stalhand propuso un método para la determinación de los parámetros del material para el modelo de Holzapfel a partir de datos clínicos [35]. Masson et al emplea un modelo similar para la determinación de estos parámetros [25]. Otros autores han utilizado este modelo para cuatro familias de fibras con el propósito de describir las propiedades de las fibras en la dirección circunferencial y longitudinal [5, 39].
ANISOTROPÍA CON TRES FAMILIAS DE FIBRAS
Se han desarrollado modelos de comportamiento anisótropo con tres direcciones preferentes que han sido aplicados en materiales biológicos, destacándose el Modelo de Fung [12, 24]: ecuación 25
Siendo EAB las componentes de Green  .
.
En ABAQUS se ha implementado el modelo de Fung con la siguiente forma, ecuación 26:
Donde:
c, D son parámetros que dependen de la temperatura.
Jel: relación volumen elástico definido como expansión térmica.
Q se define como, ecuación 27:
Donde es un tensor simétrico adimensional de cuarto orden de las constantes del material anisotrópico y que depende de la temperatura y ![]() son componentes modificadas del tensor de deformación de Green.
son componentes modificadas del tensor de deformación de Green.
Este modelo fue comparado con el de Holzapfel [16], ecuación 22, usando la arteria carótida, joven y sana, en un modelo multicapas. Para el modelo de Fung 3D, se requieren siete parámetros constitutivos del material para una sola capa, que no pueden ser escogidos arbitrariamente pues se debe asegurar la estabilidad y convexidad del material. Este modelo es limitado para simetría cilíndrica y no considera las deformaciones cortantes. El modelo 2D tiene la ventaja de que los parámetros del material se pueden obtener con facilidad pero no satisface la condición de elipticidad. Mientras, el modelo de Holzapfel es capaz de modelar las dos capas para geometrías arbitrarias y solo necesita cinco parámetros del material tanto si se considera un estado de deformación en 2D o en 3D y es capaz de modelar las tensiones residuales.
CONCLUSIONES
El modelo isotrópico de Demiray ha demostrado que no es capaz de describir el marcado comportamiento anisotrópico que ha sido observado en los estudios experimentales de las arterias. Este modelo puede ajustarse adecuadamente al comportamiento de la pared en determinadas patologías como el síndrome de Marfan o el comportamiento de la placa ateromatosa, aunque según Soler no es adecuado para arterias sanas.
El modelo de Holzapfel asume que la elastina al igual que la matriz del material no colagenoso, tiene un comportamiento isotrópico, sin embargo, estudios realizados como los de Rezakhaniha y Weisbecker sugieren que en realidad el comportamiento de ambos es anisotrópico. Asimismo Rezakhaniha, et al sugieren que existen cuatro familias de colágeno en lugar de dos como plantea el modelo ya que se observan cuatro direcciones principales cuando la arteria se encuentra libre de cargas y las fibras de colágeno se mantienen en ondas.
El modelo propuesto por Fung, tiene como desventaja que requiere un mayor numero de parámetros constitutivos del material para una sola capa. Estos parámetros no pueden ser escogidos arbitrariamente pues se debe asegurar la estabilidad y convexidad del material, lo que dificulta su empleo.
De los modelos existentes en la literatura, el modelo de Holzapfel ha demostrado ser apropiado no solo para la modelación del tejido arterial en arterias sanas sino también para simular el comportamiento de otros tejidos blandos del organismo. Este modelo lo han utilizado Alastrue, Ciarletta y Zulliger para simular el comportamiento de otros tejidos blandos.
REFERENCIAS
1. Agianniotis, A., Rezakhaniha, R. y Stergiopulos, N. "A structural constitutive model considering angular dispersion and waviness of collagen fibres of rabbit facial veins". BioMedical Engineering OnLine. 2011, vol. 10, nº. 18, p. 1-18. ISSN 1475-925X. DOI 10.1186/1475-925X-10-18
2. Alastrué, V., Peña, E., Martínez, M. A., et al. "Experimental study and constitutive modelling of the passive mechanical properties of the ovine infrarenal vena cava tissue". J. Biomech. 2008, vol. 41, nº. 14, p. 3038-3045. ISSN 0021-9290. DOI 10.1016/j.jbiomech.2008.07.008.
3. Ambrosi, D., Ateshian, G. A., Arruda, E. M., et al. "Perspectives on biological growth and remodeling". Journal of the Mechanics and Physics of Solids. 2011, vol. 59, p. 863-883. ISSN 0022-5096. DOI 10.1016/j.jmps.2010.12.011.
4. Awrejcewicz, J. C., M., Wlodarczyk, K., et al. "Finite element method analysis of non - linear behaviour of implants and stents". En: European Congress on Computational Methods in Applied Sciences and Engineering. Barcelona, España. 2000.
5. Baek, S., Gleason, R. L., Rajagopal, K. R., et al. "Theory of small on large: potential utility in computations of fluid-solid interactions in arteries". Comput. Meth. Appl. Mech. Eng. 2007, vol. 196, p. 3070-3078. ISSN 0045 7825. DOI 10.1016/j.cma.2006.06.018.
6. Balzani, D., Brinkhues, S. y Holzapfel, G. A. "Constitutive framework for the modeling of damage in collagenous soft tissues with application to arterial walls". Comput. Methods Appl. Mech. Engrg. 2012, vol. 213, p. 136-151. ISSN 0045 7825. DOI 10.1016/j.cma.2011.11.015.
7. Ciarletta, P., Dario, P., Tendick, F., et al. "Hyperelastic model of anisotropic fiber reinforcements within intestinal walls for applications in medical robotics". Int. J. Robot. Res. 2009, vol. 28, nº. 10, p. 1279-1288. ISSN 1741-3176. DOI 10.1177/0278364909101190.
8. Delfino, A., Stergiopulos, N., Moore, J. E., et al. "Residual strain effects on the stress field in a thick wall finite element model of the human carotid bifurcation". J. Biomech. 1997, vol. 30, p. 777-786. ISSN 0021-9290. DOI 10.1016/S0021-9290(97)00025-0.
9. Famaey, N., Kuhl, E., Holzapfel, G. A., et al. "Cardiovascular Tissue Damage: An Experimental and Computational Framework". En: Computer Models in Biomechanics. Netherlands: Springer Science+Business Media Dordrecht. 2013. p. 129-148. ISBN 978-94-007-5464-5. [Consultado el: 10 de abril 2014]. Disponible en: http://www.biomech.tugraz.at/images/pdf/Famaey_Kuhl_Holzapfel_VanderSloten-Book-2012.pdf
10. Famaey, N., Sommer, G., Sloten, J. V., et al. "Arterial clamping: Finite element simulation and in vivo validation". Journal of the Mechanical Behavior of Biomedical Materials. 2012, vol. 12, p. 107-118. ISSN 1751 6161. DOI 10.1016/j.jmbbm.2012.03.010
11. Fung, Y. C. Mechanical properties of living tissues. 2nd ed. New York, USA: Springer-Verlag, 1993. p. 242-251. ISBN 0387979476
12. Garcia H., C. Comportamiento Mecánico de la Aorta Ascendente: Caracterización Experimental y Simulación Numérica. Tutor: Guinea Tortuero, G. y Goicolea Ruigómez, J. M. Tesis Doctoral. Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos, Universidad Politécnica de Madrid, Madrid, España. 2008.
13. Holzapfel, G. "Determination of material models for arterial walls from uniaxial extension tests and histological structure". Journal of Theoretical Biology. 2006. vol. 238, p. 290-302. ISSN 0022-5193. DOI 10.1016/j.jtbi.2005.05.006.
14. Holzapfel, G. A., Gasser, T. C. y Ogden, R. W. "A new constitutive framework for arterial wall mechanics and a comparative study of material models". Journal of Elasticity. 2000, vol. 61, p. 1-48. ISSN 1573-2681. DOI 10.1023/A:1010835316564.
15. Holzapfel, G. A., Sommer, G., Gasser, C. T., et al. "Determination of the layer-specific mechanical properties of human coronary arteries with non-atherosclerotic intimal thickening, and related constitutive modelling". Am. J. Physiol. Heart Circ. Physiol. 2005, vol. 289, p. H2048-H2058. ISSN 0363-6135. DOI 10.1152/ajpheart.00934.2004.
16. Holzapfel, G. A., Gasser, T. C. y Ogden, R. W. "Comparison of a structural model with a Fung-type model using a carotid artery: issues of material stability". En: Proceedings of the 1st GAMM Seminar on Continuum Biomechanics. 2005, University of Stuttgart, Alemania. p. 79-89.
17. Holzapfel, G. A. y Ogden, R. W. "Constitutive modelling of arteries". The Royal Society. 2010. vol. 466, p. 1551-1597. ISSN 1742-5662. DOI 10.1098/rspa.2010.0058.
18. Hoppmann, W. H. y Wan, L. "Large deformation of elastic tubes". J. Biomech. 1970, vol. 3, p. 593-600. ISSN 0021-9290. DOI 10.1016/0021-9290(70)90043-6.
19. Humphrey, J. D. "Continuum biomechanics of soft biological tissues". Proc R Soc Lond A. 2003, vol. 459, p. 3-46. DOI 10.1098/rspa.2002.1060.
20. Khamdaeng, T., Luo, J., Vappou, J., et al. "Arterial stiffness identification of the human carotid artery using the stress-strain relationship in vivo". Ultrasonics. 2011, vol. 52, nº. 3, p. 402-411. ISSN 0041-624X. DOI 10.1016/j.ultras.2011.09.006.
21. Khanafer, K., Schlicht, M. S. y Berguer, R. "How Should We Measure and Report Elasticity in Aortic Tissue?". European Society for Vascular Surgery. 2013, vol. 45, nº. 4, p. 332-338. ISSN 1078-5884. DOI 10.1016/j.ejvs.2013.10.018.
22. Kojié, M., et al. Computer Modeling in Bioengineering. Theoretical Background, Examples and Software. West Sussex, England: John Wiley & Sons Ltd. 2008. p. 201-215, 249-264. [Consultado el: 18 de febrero 2014]. Disponible en: http://www.researchandmarkets.com/reports/2174636/computer_modeling_in_bioengineering_theoretical.pdf ISBN 978-0-470-06035-3.
23. Kyriacos, A. y Natoli, R. M. Introduction to Continuum Biomechanics. En: Synthesis lectures on biomedical engineering #19. Connecticut USA: University of Connecticut, 2008, [Consultado el: 18 de febrero 2014]. Disponible en: http://dx.doi.org/10.2200/S00121ED1V01Y200805BME019. ISBN 9781598296181.
24. Labrosse, M. R., Beller, C. J., Mesana, T., et al. "Mechanical behavior of human aortas: Experiments, material constants and 3-D finite element modeling including residual stress". Journal of Biomechanics. 2009, vol. 42, p. 996-1004. ISSN 0021-9290. DOI 10.1016/j.jbiomech.2009.02.009
25. Masson, I., Boutouyrie, P., Laurent, S., et al. "Characterization of arterial wall mechanical behavior and stresses from human clinical data". Journal of Biomechanical engineering. 2009, vol. 41, nº. 12, p. 2618-2627. ISSN 0148-0731. DOI 10.1016/j.jbiomech.2008.06.022.
26. Murtada, S. I., Kroon, M. y Holzapfel, G. A. "A calcium-driven mechanochemical model for prediction of force generation in smooth muscle". Biomech Model Mechanobiol. 2010, vol. 9, p. 749-762. ISSN 1617-7940. DOI 10.1007/s10237-010-0211-0.
27. Ogden, R. W. "Anisotropy and nonlinear elasticity in arterial wall mechanics". En: Biomechanical modelling at the molecular, cellular and tissue levels. Vienna, Austria: Springer. 2009. p. 179-258. ISBN 978-3-211-95875-9. [Consultado el: 6 de enero 2014]. Disponible en: http://shellbuckling.com/cv/ogden.pdf
28. Pezzani, A. y García Herrera, C. "Caracterización del comportamiento mecánico de la aorta descendente". En: Anales de Mecánica de la Fractura 28. Santiago de Chile, Chile. 2011. [Consultado el: 18 de diciembre 2013]. Disponible en: http://www.gef.es/Congresos/28/pdf/Anales28-009.pdf
29. Rachev, A. y Hayashi, K. "Theoretical Study of the Effects of Vascular Smooth Muscle Contraction on Strain and Stress Distributions in Arteries". Biomedical Engineering Society. 1999, vol. 27, p. 459-468. ISSN 1573-9686.
30. Rezakhaniha, R., Fonck, E., Genoud, C., et al. "Role of elastin anisotropy in structural strain energy functions of arterial tissue". Biomech Model Mechanobiol. 2011, vol. 10, p. 599-611. ISSN 1617-7940. DOI 10.1007/s10237-010-0259-x.
31. Rezakhaniha, R., Agianniotis, A., Schrauwen, J. T. C.,et al. "Experimental investigation of collagen waviness and orientation in the arterial adventitia using confocal laser scanning microscopy". Biomech Model Mechanobiol. 2012, vol. 11, p. 461-473. ISSN 1617-7940. DOI 10.1007/s10237-011-0325-z.
32. Roy, S., Boss, C., Rezakhaniha, R., et al. "Experimental characterization of the distribution of collagen fiber recruitment". Japanese Society of Biorheology. 2010, vol. 24, p. 84-93. ISSN 1867-0474. DOI 10.1007/s12573-011-0027-2.
33. Soler, J. R. Modelos numéricos para mecánica cardiovascular de las paredes arteriales y sus procesos de adaptación. Tutor: Goicolea Ruigómez, J. M. Tesis Doctoral, Universidad Politécnica de Madrid, Madrid, España. 2003.
34. Spencer, A. J. M. Continuum Theory of the Mechanics of Fibre-Reinforced Composites Courses and lectures, nº 282. New York, USA: Springer-Verlag, 1984. ISBN 9780387818429.
35. Stilhand, J. "Determination of human arterial wall parameters from clinical data". Biomech. Model. Mechanobiol. 2009, vol. 8, nº. 2, p. 141-148. ISSN 1617-7940. DOI 10.1007/s10237-008-0124-3.
36. Watton, P. N., Ventikos, Y. y Holzapfel, G. A. "Modeling the mechanical response of elastin for arterial tissue". Journal of Biomechanics. 2009, vol. 42, p. 1320-1325. ISSN 0021-9290. DOI 10.1016/j.jbiomech.2009.03.012.
37. Weisbecker, H., Viertler, C., Pierce, D. M., et al. "The role of elastin and collagen in the softening behavior of the human thoracic aortic media". Journal of Biomechanics. 2013, vol. 46, p. 1859-1865. ISSN 0021-9290. DOI 10.1016/j.jbiomech.2013.04.025.
38. Yang, W., Fung, T. C., Chian, K. S., et al. "Directional, regional, and layer variations of mechanical properties of esophageal tissue and its interpretation using a structure-based constitutive model". J. Biomech. Eng. 2006, vol. 128, p. 409-418. ISSN 0148-073. DOI 10.1115/1.2187033.
39. Zeinali Davarani, S., Choi, J. y Baek, S. "On parameter estimation for biaxial mechanical behavior of arteries". J. Biomech. 2009, vol. 42, p. 524-530. ISSN 0021-9290. DOI 10.1016/j.jbiomech.2008.11.022.
40. Zulliger, M. A., Rachev, A. y Stergiopulos, N. "A constitutive formulation of arterial mechanics including vascular smooth muscle tone". J Physiol Heart Circ Physiol. 2004, vol. 287, p. 1335-1343. ISSN 1522-1539. DOI 10.1152/ajpheart.00094.
Recibido: 21 de abril de 2014.
Aceptado: 10 de agosto de 2014.
Diana Otero-Martínez. Instituto Superior Politécnico José Antonio Echeverría, Facultad de Ingeniería Mecánica. La Habana, Cuba.
Correo electrónico: diani.81@gmail.com