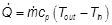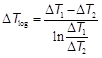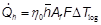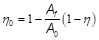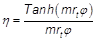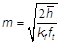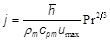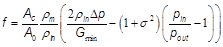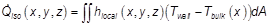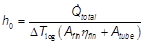Introduction
A high-energy loss in most industrial or domestic processes is caused in the heat transfer process due to the temperature difference between the fluids. Often one of the working fluids is air since it is a clean, cheap and stable material but usually comes with a high thermal resistance. To reduce fuel and power consumption as well as to lower climate-damaging gas emissions compact heat exchangers regularly use interrupted surfaces. Wavy, louver, slit fins and many more are widely used to increase the thermal performance by preventing the formation of thick boundary layers and creating high turbulence in the heat exchanger. The effects of fin pitch, number of tube row and other geometrical characteristics have been investigated extensively and still there are researches going on. A lot of them are of experimental nature but since computing power is increasing also numerical studies using computational fluid dynamics (CFD) are elaborated like the current article.
Wang et al. [1] conducted an experimental study on the air side performance of compact slit fin-and-tube heat exchangers and found that it is relatively independent on the number of tube rows and the fin pitch. However, they only studied two different fin pitches in this work. Using various comparison methods, they evaluated the results with the louver and plain fin. They discovered that the air side performance of interrupted fins is superior to that of the plain fin but this difference decreases with lower fin pitch and Reynolds number. An updated correlation was proposed and is considered in the current paper to certify the numerical model with experimental data.
However in a different article Wang et al. [2] studied experimentally the airside performance of fin-and-tube heat exchangers, having a different slit geometry and came to the conclusion that the heat transfer performance increases with decrease of fin pitch for only one tube row (N). For N > 4, the effect of fin pitch on the heat transfer performance was reversed and the heat transfer performance decreased with increased number of tube row. The friction factor was found relatively independent to the number of tube row. Borrajo-Perez et al. [3] investigated the thermal-hydraulic characterization of a compact heat exchanger having two rowsof tubes and rectangular wavy fins and used the proposed correlations in Wang et al. [1] to certify the numerical procedureand its mathematical model against published literature.
Also Wang et al. [4] carried out a study on convex louver finswere the heat transfer data was presented as a multiplicationof the fin efficacy 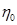 by the average heat transfer coefficient
by the average heat transfer coefficient . The separation of the fin efficiency and the heat transfer coefficient were based on the Schmidt method, which also will beused in this paper. The Colburn and Fanning friction factor arecalculated using the correlations utilized by Wang et al. [5] inan experimental study on the airside performance of a herringbone wavy fin. The conclusions for modeling and simulating acompact heat exchanger will be used in the current paper. Interrupted fins have a quite complex geometry and to studythe heat transfer coefficient the fin efficiency is not determined precisely by the Schmidt method, which performs better for continuous fin designs. This is because the heat transfer conduction inside the solid is disturbed and several changes in the fin temperature distribution can be found in interrupted fins. In numerical studies, it is possible to determine the fin efficiency and heat transfer coefficient directly. Unfortunately many papers working with interrupted fins still are using the approximate Schmidt method [6]
. The separation of the fin efficiency and the heat transfer coefficient were based on the Schmidt method, which also will beused in this paper. The Colburn and Fanning friction factor arecalculated using the correlations utilized by Wang et al. [5] inan experimental study on the airside performance of a herringbone wavy fin. The conclusions for modeling and simulating acompact heat exchanger will be used in the current paper. Interrupted fins have a quite complex geometry and to studythe heat transfer coefficient the fin efficiency is not determined precisely by the Schmidt method, which performs better for continuous fin designs. This is because the heat transfer conduction inside the solid is disturbed and several changes in the fin temperature distribution can be found in interrupted fins. In numerical studies, it is possible to determine the fin efficiency and heat transfer coefficient directly. Unfortunately many papers working with interrupted fins still are using the approximate Schmidt method [6]
In the study of Ameel et al. [7] was shown that the Schmidt correlation for a fin having a complex, interrupted design results in an over estimation of the fin efficiency. They proposed a new numerical method other than the often used ratio of the actual heat transfer rate to the heat transfer rate for an isothermal fin, which they proved to be not consistent because  and LMTD are not constant. The flow pattern in a compact heat exchanger area is so complex that parametric studies are needed [8-9]. The next step in field of heat exchangers is the use of heuristic algorithms to simplify the task of parametric studies [10]
and LMTD are not constant. The flow pattern in a compact heat exchanger area is so complex that parametric studies are needed [8-9]. The next step in field of heat exchangers is the use of heuristic algorithms to simplify the task of parametric studies [10]
Glazar et al. [11] varied the fin pitch in a wavy fin-and-tube heat exchanger from 0,4 to 4mm and the results showed that there is an optimal fin pitch for each air velocity, which gives the best heat exchanger performance just from the heat transfer point of view. Therefore, three different fin pitches will be examined in the following.
From the literature reviewed can be noted that is not clear the influence of the fin pitch on the thermo-hydraulic behavior of slit fin having one row of tubes. On the other hand, the fin efficiency using the Schmidt method is not appropriate for interrupted fins. The objective was to obtain the thermal-hydraulic behavior for different fin pitches while ranging the Reynolds number from 400 to 1800 using a novel reported method for fin efficiency determination [7].
Methods and Materials
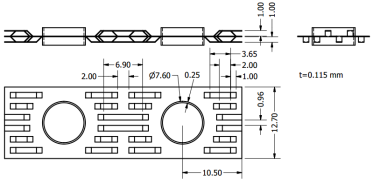
In this study, a model of a fin-and-tube heat exchanger having slit fin geometry is investigated. The related geometry is illustrated in figure 1. The present fin has an offset slit geometry and for an accurate differentiation, the plate fin will be just called “fin” and the offsets “strips”. After the numerical validation, a model with slightly bigger strips and three different fin pitches is examined.
Computational Domain
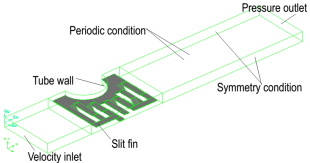
The geometry of the fin used in this work was modeled in the Inventor software. A model having only one row of tubes is presented in this work. For the three-dimensional physical domain, a fin was set in the middle and consecutive one-half of the fin pitch in both directions. When the heat transfer and the flow conditions are periodic in the upper and lower side of the fin, it is very simple to implement this boundary condition in the two parallel planes at the top and the bottom of the flow domain. The size and the design of the model are similar as in the real heat exchanger. In width, there was only figure. 2 presents the computational domain with the boundaryconditions labeled. The fin can be observed in the middle of the channel and its surface is shaded.
Two regions were artificially extended in the computational domain. The one at the up stream is as long as the channels width for considering the inlet effects and downstream ofthe fins trailing edge the channel was extended three times its width. The extensions of the computational domain have a bigimpact on computational time but are necessary to show exit effects and avoid reversal flow at the exit. Two regions with symmetrical boundary conditions were established at both sidesof the domain and two periodic boundary condition were set attop and bottom. A velocity inlet condition at inlet section and pressure outlet condition at outlet section were established. Aboundary condition of constant temperature at 286K was used at the tube wall.
On the fins surface a wall-coupled boundary condition wasapplied to consider the conjugate heat transfer on the surface. The computational domain was meshed in the GAMBIT software and the grid quality was checked. Several sub domainswere used to make the grid generation smoother. Approximately 5,4x105 tetrahedral volumes were generated for thefinest mesh with 0,115mm length of the edges which is alsothe fin thickness (ft). Heat transfer and fluid flow simulations were performed using the commercial solver FLUENT. The material propertiesare found in table 1 and are considered constant.
Table 1 Material properties used in the numerical simulation
| Material | Density (kg/m3) | Specific heat capacity (J/kgK) | Thermal conductivity (W/mK) | Viscosity (N-s/m2) |
|---|---|---|---|---|
| Air | 1,225 | 1006,43 | 0,0242 | 1,789E-5 |
| aluminum | 2719 | 871 | 202,4 | - |
The air is assumed incompressible and the viscousmodel laminar. During the calculation, a segregated solver withconstant properties was considered and to ensure mass conservation as well as to obtain a pressure field the SIMPLE algorithm for the coupling between pressure and velocity was implemented. Scale residuals were monitored and convergencecriteria was set to 10−8 for energy and 10−4 for continuity. Thediscretizationapplied was standard for pressure, first order upwind for momentum and second order upwind for energy. The second order schemewas selected considering the misalignment between the flowand the grid. This decision helps to avoid the effect of numerical diffusion in misaligned grids. In general, the time elapsedfor every solution was less than one hour in a specialized computer.
Data Reduction Procedure
The Reynolds number (Re) is determined using the velocity umaxat the minimal area of the channel. The characteristiclength is the fin collar diameter Dc.Heat transferred in a heatexchanger (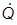 ) can be calculated with the change in temperature of the air between the inlet and outlet sections (Tout− Tin), themass flow through the heat exchanger channel (m) and knowing the fluid’s specific heat capacity cp. Equation 1
) can be calculated with the change in temperature of the air between the inlet and outlet sections (Tout− Tin), themass flow through the heat exchanger channel (m) and knowing the fluid’s specific heat capacity cp. Equation 1
When a fluid experiences a phase change inside tubes it is a common practice to consider an elevated value for the film heattransfer coefficient inside the tubes. This assumption is important because a global heat transfer coefficient can be obtained considering only the external film heat transfer coefficient andperfect conduction inside the tube wall. The walls temperature is set constant and with the same value than the refrigerant temperature flowing inside the tubes.
The LMTD correction factor F is considered unitary becauseone of the fluids flowing through the heat exchanger keeps aconstant temperature. The global heat transfer coefficient iscalculated considering the equality of the heat calculated by theequations 1 and 3. The efficacy η 0 of the fin is involved and at the same time, itis a function of the global heat transfer coefficient. For this, theefficacy can be calculated if the fin efficiency η is known. A f /A 0is the rate of heat transfer area to the total area of the fin, as in equation 4.
The heat transferred (equation 4) can be calculated using the logarithmic mean temperature difference LMTD in equation 2 and by knowing the heat transfer area A f and the global heat transfer coefficient.
The fin efficiency for the rectangular fin is determined usingan approximate method developed by Schmidt for circular finsand further explained by Wang et al. [4]. The fin efficiency isexpressed by equation 5:
the parameter m is calculated with the thermal conductivity (kf)of the fin and the fin thickness (f t ) equation 6:
The term is obtained with the equivalent tube radio dividedby the tube radio (R
eq
/r
t
). This parameter is just depending onthe heat exchanger geometry. Equation 7
is obtained with the equivalent tube radio dividedby the tube radio (R
eq
/r
t
). This parameter is just depending onthe heat exchanger geometry. Equation 7
With, equation 8:
WhereX M is the half-transversal pitch and X L is calculated bythe following equation, where S T and S L are the transversal andlongitudinal pitch respectively equation 9:
The fin efficacy and the global heat transfer coefficient have animplicit formulation;there for, an iterative procedure is needed.The condition of equality of the heats in equation 5 must beachieved. For a fixed geometry, there is only one pair of values in fin efficacy and global heat transfer coefficient, whichmeets this requirement. The Colburn factor j can be calculated having the global heattransfer coefficient, the velocity in the minimal cross section ofthe channel u max , the heat capacity at constant pressure of theair, the Prandtl number (Pr) and the average air density equation 10:
The friction factor f is used for the hydraulic characterizationof the heat exchanger model. The Fanning friction factor iscalculated using the Kay and London definitionapud [12] for a fluid with constant properties, where A c is the minimum flow area. σ is the contraction area ratio, ∆p isthe pressure drop and G min is the mass flux in the minimal flowarea, equartion 11:
For evaluating the fin efficiency,the numerical method fromAmeel et al. [7] can be implemented. Since Wang et al. [1] wasusing the Schmidt’s method it cannot be used for finding correlations but only for validation of the fin efficiency as functionof inlet velocity and fin pitch. Fourteenplanes constant in the x-axiswere created through the channel with 1mm distance to eachother starting at the first edge (x 1=0,01m) until the end of thefin. Within each one of the planes an average temperature of thefluid phase is calculated, that will be called “bulk temperature”, equation 12.
For each inlet velocity, the values are obtained anda regression is performed.With this temperature trend, the local heat transfer coefficients equation 15 are calculated with the local heat flux and fin temperatures.
An ideal fictitious heat flux is then determined as if for isothermal conditions in equation 14:
The fin efficiency is obtained in equation 15 by the ratio of the real to the isothermal heat flux, equation 15.
For a fin pitch of Fp= 1,81mm the values of the heat transfercoefficient and pressure drop are used to calculate the Colburnand the friction factor. These values are represented in the figure 3 and compared to the results obtained by Wang et al [1]. Theuncertainties in the reference are expressed for j and f. Thefigure shows a good match between experimental and simulateddata obtained in this work and validates the numerical model. The independence of mesh and resolution is given through figure 4 where data for Colburn and friction factor are plotted fora coarse mesh with a total number of 3,5x105 volumes and in the second, finer one with 5,4x105 volumes.
Fig. 3 Colburn and friction factor for experimental and numerical data comparison (left).Colburn and friction factor to compare results of different meshed domains (right)
Results and Discussion
Simulated velocities range from 0,1 to 2,0 m/sbut for this article only the ones higher than 0,5m/s are considered since only Reynolds numbers significantly larger than 200 are customary for compact heat exchangers. The numerically computed fine fficiency has a peak at around u in = 0,3m/sand falls rapidly for smaller velocities what could be due to the heat reversal problem occurring at the end of the fin and in the wake area. A similar problem of heat transfer reversal was studied in thework of Fiebig et al [13].
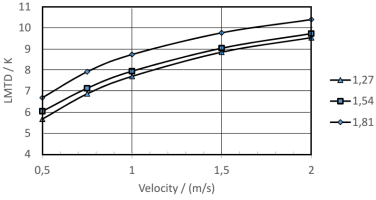
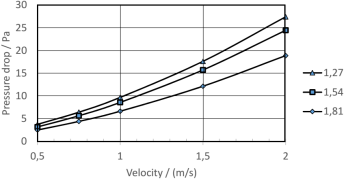
The simulation shows for the logarithmic temperature difference (LMTD), mass flow and pressure drop nearly uniformand predictable results. With higher fin pitch the logarithmic temperature difference in figure 5 increases as well as with rising inlet velocity of the air.
The pressure drop in figure 5 followsquadratic behavior and gets smaller for higher fin pitch. Thetemperature at the outlet varies between 286K and 293K. Withhigher inlet velocity and greater fin pitch the outlet temperature rises because there is less time for the heat transfer from fluid to solid, higher mass flow and greater ratio of channel volume to heat conduction surface.
The numerical calculated fin efficiency equation 17 is be plotted in figure 6 for every fin pitch and inlet velocity. Note that the behavior for F, p=1,81mm and Fp=1,54mm is quite similar while the curve for fp=1,27mm has greater values than the others except for the first data point do.
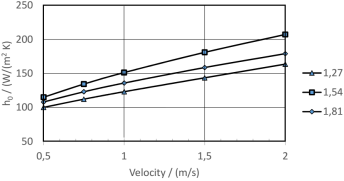
Wang et al[2] described the increase of heat transfer performance with a decrease of the fin pitch. This could be ones expectation because the ratio of real to the ideal fictitious heat flux equation 15 is getting steadily smaller. With this interpretation in mind, the heat transfer coefficient h 0 which is calculatedwith the equation 16would increase. The data shows a different, not expected performance for both fin efficiency and heat transfer coefficient, figure 7.
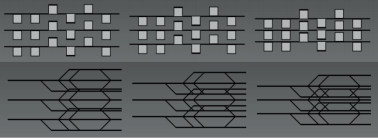
Fig. 8 Side views of the stacked fins in z-axis (upper drawing) and in x-axis(lower drawing) to see the distribution of the slits starting with highest fin pitchon the left
The quite different performance is explained due to the distribution of the strips that is shown in figure 8 where two periods of the stacks geometry are illustrated. While the one withf p =1,54mm has a quite evenly spread geometry, the otherones have whether offset strips that are very close to the fin inz-direction or that are overlapping when looking in x-direction.
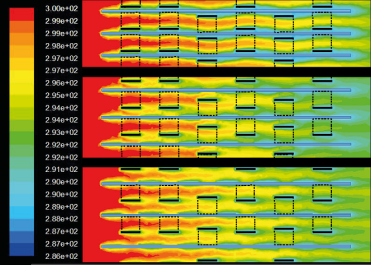
Fig. 9 Temperature field for an inlet velocity of 2,0 m/s starting with the lowest fin pitch at the top
Of course, this affects the boundary layers produced by the airflow. In figure 9 the fluids temperature is shown for all the fin pitches at an inlet velocity of 2.0m/s. For the sack of simplicity, the plate fin is drawn as a light blue rectangle without the slits and the dotted lines significance the backside of the offset strips. The upper drawing represents the temperature boundary layersfor f p =1,27mm. The strips are located very close to the eachopposite fin surface where boundary layers are already startingto develop. There the temperature gradient is lower than in thefree stream in the middle between the two fins where it is ableto flow with very few interruptions.
The configuration with f p =1,81mm shows that the stripsfrom the both subsequent fins are one after another nearly inthe same line of stream flow. This is already better than the firstconfiguration because they are found right in theuntil then notdisturbed flow and produce new boundary layers.
Still the heat is not being exchanged very well in comparison to the second configuration where the strips lie in themiddle between the fins and alternate in their distance to them. They divide the flow various times what results in more turbulence, higher local heat fluxes and explains the special characteristics in figure 9. This configuration is also producing an about10% greater pressure loss in flow compared to the setup with f p =1,81mmand hence to an elevated power consumption of the fan.
For the heat flux on the fin surface in figure 10, the leading edges always show the highest values and one can note, that the strips inthe middle of the fins appear to have the most noticeable change for different fin pitches. The figure may lead to the conclusionthat for f p =1,54mmthe most energy is transmitted but stillthere needs to be considered, that the highest total heat transferis monitored for the maximal fin pitch because the mass flow aswell as the temperature difference are greater at a constant inletvelocity. In addition, the tube wall exchanges energy and it gets largerwith increasing fin pitch.
For the Colburn factor figure 11 the model with fp=1,54mmshows the highest thermal performance, while for the frictionfactor has the worst hydraulic performance. This fitsto the former observations made in this paper. We suppose anoptimal fin pitch could be found for this geometry and underthe conditions tested in this paper.A commonly used criterion to evaluate the thermal-hydraulicperformance of a heat exchanger is the area goodness factor. Itis defined as the ratio of the Colburn to the friction factor. Highvalues of j/f are preferred as this means less frontal area for afixed heat transfer and pressure drop according to Stone [14].The area goodness factor is plotted in figure 12 and may suggestfp=1,54mmas the best configuration LaHaye et al [15] suggested evaluating the thermalhydraulic performance of heat exchangers by plotting the heattransfer performance factor J as function of thepumping power factor F which is done in figure 12.The model with fp=1,54mmhas a better thermal performance for the same pumping power when compared to the otherones.

Fig. 11 Colburn factor and Friction factor for three different fin pitches as a function of the inlet velocity
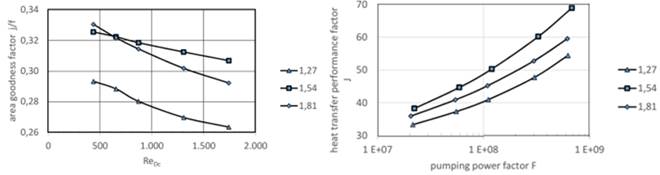
Fig. 12 Area goodness factor of the Reynolds number for different finpitches (left) and evaluation of the thermal-hydraulic performance according to LaHaye et al. [11] (right)
Conclusions
The average heat transfer coefficient as a function of the fin pitch isat its best when the strips of one fin have the same distanceto the ones of the opposite arranged fin as to their fin plate.So the highest heat flux and turbulence is achieved. The model with f p = 1,54 mmhas the best thermal performance for the same pumping power. The fin efficiency as a function of the inlet velocity has apeak for each fin pitch. For velocities smaller than thepeak, it falls rapidly wherefore heat transfer reversal couldbe responsible for this fact. The calculation of fin efficiency via the Schmidt method is not adequate on interrupted fins.