Introducción
Las transmisiones por engranajes son uno de los modos más utilizados en el sistema de transmisión de potencia, debido a sus ventajas como son: alta potencia, alta eficiencia y larga vida útil. En las últimas décadas se ha trabajado en aumentar la robustez de los elementos de máquinas de tal manera de hacer estos elementos cada vez menos sensibles a variaciones en las condiciones de operación. Los estándares existentes para el diseño de transmisiones por engranajes utilizan procedimientos previamente establecidos que no permiten evaluar con precisión la robustez de estas transmisiones y se limitan a incluir un gran número de factores de corrección para tener en cuenta diversas incertidumbres [1,2]. En [3] se realiza un profundo estudio del efecto de varios parámetros sobre la resistencia a la flexión de los engranajes cilíndricos de dientes rectos de evolvente, considerando las incertidumbres en parámetros geométricos como radio del filete, ancho de cara, etc. También se estudian las incertidumbres en las propiedades del material que afectan la resistencia de los dientes del engranaje, sin embargo, no se evalúa la influencia de dos parámetros geométricos importantes como son la asimetría y la corrección del dentado, así como la combinación de ambos en la resistencia del diente.
El diseño y la optimización de las transmisiones de engranajes han sido intensamente estudiados, pero sorprendentemente la robustez del diseño óptimo resultante a cargas inciertas nunca ha sido considerada. En [4] se desarrolla una metodología denominada Active Robust para diseñar productos que logren robustez a condiciones ambientales inciertas o cambiantes a través de la adaptación. Este problema se formula como un problema de optimización bi-objetivo donde los objetivos son satisfacer la demanda de carga de la manera más eficiente y minimizar el costo de producción. Los resultados muestran que este enfoque puede encontrar un conjunto de diseños robustos, revelando un equilibrio entre la eficiencia energética y el costo de producción. En [5] se utiliza el diseño de experimentos de Taguchi y la computación para predecir la capacidad de carga de un engranaje planetario. La aplicación del Diseño de Experimentos de Taguchi se usó para obtener un modelo de regresión lineal para predecir un valor nominal de factor de seguridad, indicando la máxima carga aplicable al conjunto de engranajes basándose en los parámetros de entrada elegidos para reducir la falla de la transmisión de potencia y un mejor rendimiento durante el funcionamiento. La aplicación de este enfoque es demostrar la ventaja de combinar el método de Taguchi para el Diseño de Experimentos con la Ingeniería Asistida por Computadoras (CAE) para alcanzar la solución deseada, siendo esta una de las vertientes utilizadas en el presente trabajo.
El diseño robusto se ha desarrollado con la expectativa de que se puede obtener un diseño insensible a factores externos (variación de las fuerzas, la temperatura, etc). Las teorías del diseño robusto se han perfeccionado adoptando las teorías de otros campos. Basado en las teorías, el diseño robusto se puede clasificar en tres métodos: 1) el método de Taguchi, 2) optimización robusta, y 3) diseño robusto con el enfoque axiomático [6].
En [7], se introduce una de las primeras variaciones a los métodos de Diseño Robusto de Taguchi. En estos métodos, existen dos grandes categorías de problemas asociados a minimizar simultáneamente las variaciones del comportamiento y alcanzar el objetivo deseado, es decir, Tipo I - minimizando las variaciones en el comportamiento causadas por las variaciones en los factores de ruido (parámetros incontrolables). Tipo II - minimizar las variaciones en el comportamiento causadas por variaciones en el factor de control (variables de diseño).
La robustez del diseño es un tema extenso y muy abordado en los últimos años. Según [8], un investigador anticipa la planificación de un estudio que dará lugar a una serie de observaciones sobre una variable aleatoria y, cuya distribución de probabilidad - a menudo simplemente a través de su valor esperado depende de un vector x de covariables que puede ser fijado por el investigador. Después de reunir los datos, se evaluará la relación entre "y" y "x". Esto generalmente implicará tanto la estimación como la predicción y se hace a menudo en el contexto de un modelo particular del cual el experimentador podría tener sólo un conocimiento parcial y en el que podría tener poca fe; de ahí el requisito de robustez.
En [9] se analiza como los modelos de ingeniería se pueden utilizar para desarrollar diseños robustos. Se considera la robustez en dos niveles: viabilidad de la robustez, que se refiere a asegurar que las limitaciones de diseño se satisfacen a pesar de la variación, y "sensibilidad de la robustez", donde se desea reducir la sensibilidad del diseño a la variación. En cualquier problema de diseño en particular, se puede desear incorporar uno o ambos niveles de robustez.
En la literatura existen varios trabajos del empleo del diseño robusto a elementos mecánicos [10-12], pero pocos aplicados a las transmisiones por engranajes [5]. La optimización del diseño de engranajes ha traído en ocasiones como consecuencia que el engranaje optimizadosea menos robusto. La baja robustez, es decir, una gran variación en el comportamiento del producto, implica una alta incidencia de rechazos o mal funcionamiento, todos los cuales pueden tener un efecto negativo en los beneficios de la empresa que los produce. Dado que el uso de la optimización disminuye los márgenes de seguridad, se debe prestar mayor atención a garantizar la robustez de los productos. [13].
En este artículo se propone un nuevo parámetro denominado índice de robustez a la flexión para evaluar la robustez de los engranajes cilíndricos de dientes rectos a este tipo de solicitación. Se analiza la influencia de la corrección y la asimetría en este índice. Para lograr este objetivo se utilizó un experimento virtual, concluyéndose que a través de estos factores geométricos se puede aumentar la robustez de los engranajes a la fractura hasta en un 48 %.
Métodos y Materiales
Para evaluar la influencia de la geometría del diente (asimetría y corrección) en el índice de robustez a la fractura, se realizó un diseño de experimentos virtual con dos valores de entrada y cinco niveles de experimentación. Fueron dibujados diferentes modelos de dientes de engranajes con diferentes valores del coeficiente de asimetría y del coeficiente de corrección usando la opción de Shaf Generator del Mechanical Desktop. Estos modelos fueron exportados para el Software de Elementos Finitos Solid Work Simulation 2018 para evaluar las tensiones y deformaciones que presentaban los mismos. A continuación, se detalla todo el procedimiento efectuado.
Índice de Robustez de los engranajes cilíndricos de dientes rectos
Teniendo en cuenta los aspectos analizados de la literatura, se puede establecer el concepto de Índice de Robustez para las transmisiones por engranajes, así como los parámetros que influyen en este índice. Según el concepto de robustez, un engranaje será más robusto en cuanto más resistente sea a las variaciones o factores externos durante su funcionamiento.
Según [2], los factores que influyen en la resistencia de un engranaje son: geometría, materiales, errores de fabricación, montaje y condiciones de funcionamiento
Para poder evaluar la influencia de la geometría en la robustez de los engranajes se estableció el Índice de Robustez, que no es más que la relación entre la resistencia del engranaje con modificaciones geométricas con relación a la resistencia del engranaje sin modificaciones geométricaso, dicho de otra forma, la relación entre la tensión normal en el pie del diente del engranaje sin modificaciones, dividida por la tensión normal en el diente del engranaje con modificaciones. Por tanto, existirá un índice de robustez a la flexión, un índice de robustez a la picadura, un índice de robustez al desgaste, un índice de robustez al agarramiento, etc. En este artículo se analiza el índice de robustez a la fractura, que puede ser calculado como, ecuación 1:
Donde:
Diseño de experimentos para evaluar el índice de robustez a la fractura
Para determinar el índice de robustez a la fractura de los engranajes cilíndricos de dientes rectos exteriores, se evaluóla influencia de la asimetría, la corrección y la combinación de ambas en la resistencia a la flexión en estos engranajes. Dada la cantidad de posibles combinaciones para las variables, se realizó y se implementóun diseño experimental factorial completo para determinar la influencia de los parámetros mencionados en la robustez del diente y el número de tratamientos significativos o experimentos.Para realizar el diseño, se partió de determinados valores típicos para establecer la geometría del engranaje en cuestión. Se decidió utilizar como valores constantes el módulo igual a 4 mm, el número de dientes igual a 17; y como variables un rango de corrección y asimetría.Con estos datos se construyeron modelos de ruedas dentadas a los cuales se les colocó una carga preestablecida y se evaluaron las tensiones usando el método de los elementos finitos.
Se decidió utilizar las variables de corrección (X), asimetría (C), como variables de entrada, puesto que son las que determinan el resultado de la variable de salida: esfuerzo a flexión (
Los resultados fueron analizados para las condiciones mostradas en la tabla 1.
Tabla 1 Parámetros y valores usados en el diseño de experimentos
| Parámetro | Valores | ||||
|---|---|---|---|---|---|
| Corrección (X) | 0 | 0,25 | 0,50 | 0,90 | 1,25 |
| Asimetría (C) | 1 | 1,125 | 1,175 | 1,25 | 1,35 |
| Material | Acero AISI 1045 | ||||
| Potencia (kW) | 18,7 | ||||
| Velocidad de giro (rad/s) | 183,30 | ||||
| Fuerza Tangencial (N) | 3001,2 | ||||
| Fuerza Radial (N) | 1092,35 | ||||
| Ancho de la rueda (B) | 48 mm | ||||
| Ángulo de ataque (αa) | 20° | ||||
| Ángulo de respaldo (αr) | 20° a 27° | ||||
El ángulo de ataque del perfil se mantuvo constante en 20 grados, y el ángulo de respaldo de 20 a 27 grados.
La meta del diseño de experimentos es comparar que variables de entrada tienen mayor influencia en las variables de salida, también permite determinar un número de experimentos significativos.
Con el objetivo de analizar una población significativa de experimentos y dada las posibles combinaciones de las variables de entrada y salida, se plantean 5 niveles de experimentación que abarcan el rango lógico de variación de los factores de entrada:
n = 25
Un experimento diseñado es ortogonal si los efectos de cualquier factor se equilibran con los efectos de los otros factores. La ortogonalidad garantiza que el efecto de un factor o interacción pueda estimarse de manera independiente del efecto de cualquier otro factor o interacción presente en el modelo.
Por lo tanto, de acuerdo a las características deesta investigación, que busca determinar la influencia de los factores geométricos en la robustez del diente, donde se tienen 5 niveles de asimetría y corrección, la matriz más adecuada es la L25, para evaluar 2 factores de entrada a cinco niveles de experimentación por lo que se realizan 25 experimentos.
Creación del modelo en elementos finitos
Con los datos de la tabla 1 se fueron creando los diferentes modelos de los dientes para los diferentes valores de corrección y asimetría. Con las características geométricas definidas, utilizando el software Mechanical Desktop 2006, se puede obtener el modelo del engranaje utilizando la opción de generar árboles y ejes (Shaft Generator). Ya con los modelosde los dientes construidos, se procedió a dar todos los datos necesarios para el pre procesamiento, como son: material, condiciones de contorno, aplicación de la carga y restricciones. El material utilizado para el experimento virtual fue el AISI 1045.
Las condiciones de apoyo de la rueda se restringen a dos grados de libertad de movimiento en el área al diámetro interior y del corte de una pared del volumen de la pieza.
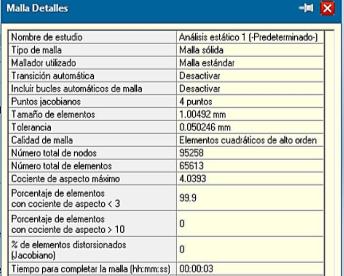
La fuerza tangencial actuante se coloca en la arista superior, perteneciente al diámetro exterior, teniendo en cuenta que a la entrada del engrane es cuando se produce el mayor momento flector en la base del diente, figura 2. El diente fue mallado con elementos TETRA 10 que poseen 10 nodos con lados parabólicos, figura 2 y tabla 2.
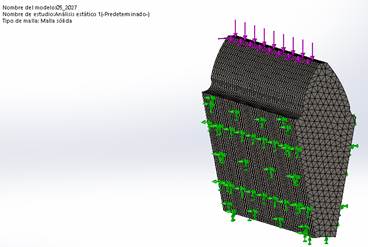
Fig. 2 Cargas y restricciones para ángulo del perfil del diente asimétrico C = 1,35 y corrección X = 0,50
El modelo fue validado y también fue realizado el análisis de convergencia. La validación del modelo tiene como objetivo aumentar su nivel de coincidencia, con respecto a un comportamiento experimental o teórico previamente obtenido. Con el objeto de verificar si el comportamiento simulado refleja adecuadamente el comportamiento real, los modelos de elementos finitos deben ser calibrados o validados con parámetros experimentales, ya sean propios o tomados de la literatura. En este caso el modelo fue validado con resultados teóricos que aparecen en [14,15]. El análisis de convergencia consiste en realizar una serie de corridas, disminuyendo paulatinamente el tamaño global del elemento con el fin de comparar los valores de los esfuerzos normales en el eje Z, que experimenta la pieza al ser cargada con una fuerza. El estudio se realizó considerando un error de +-5% para varias corridas consecutivas.
Para determinar las correcciones límites se calculó el espesor del diente por la circunferencia exterior, para ese diseño de experimentos, garantizando que ese espesor fuera mayor que el que el mínimo establecido por la literatura.Con los valores de la potencia, las dimensiones geométricas del engranaje y el número de revoluciones y aplicando las fórmulas clásicas para los engranajes cilíndricos de dientes rectos exteriores se determinaron la fuerza tangencial
Resultados y Discusión
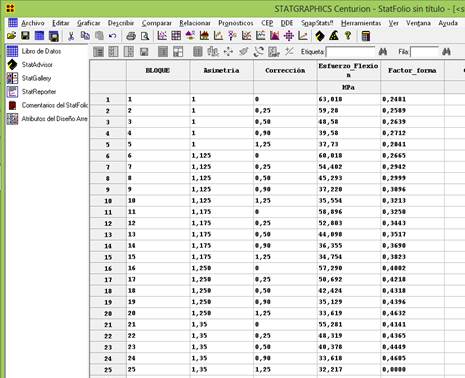
Con el empleo del diseño de experimentos factorial completo se determinaron 25 tratamientos significativos de dientes rectos exteriores asimétricoscorregidos, así como las interacciones entre las variables de entrada y salida, haciendo uso de CAD y MEF con vistas a determinar el índice de robustez a la flexión de los engranajes cilíndricos de dientes rectos exteriores. En la figura 3 se muestra el diseño completo con las variables de salida calculadas mediante CAD y MEF.
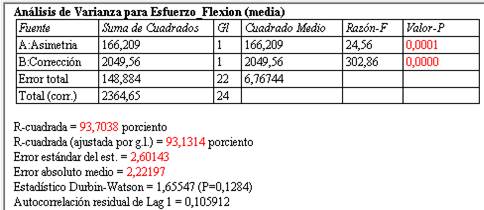
En la tabla 3 se observan los valores de la Razón-F de asimetría y corrección, que es la estadística de la prueba usada para determinar si el término está asociado con la respuesta. Un valor de la Razón-F suficientemente grande indica que el término o el modelo es significativo. Estos valores fueron determinados con el diseño factorial completo con el software Statgraphics Centurion. Se observa que la variable corrección tiene el valor más alto, por consiguiente, es la que más influencia tiene en el esfuerzo a flexión en el pie del diente.
De manera similar se obtienen los resultados de Valor-P, que se observa que son menores que 0,05, lo que permite indicar por consiguiente que hay significancia de estas variables asimetría y corrección en el esfuerzo a flexión en el pie del diente.
En la tabla 4, se muestran los valores de las tensiones normales (MPa), en el pie del diente. Estos valores fueron determinados mediante la aplicación del MEF, considerando el modelado CAD de los dientes rectos cilíndricos exteriores; lo que permite obtener una serie de valores de tensiones normales en el pie del diente para evaluar la influencia de los factores geométricos corrección y asimetría
Dichos factores geométricos influyen significativamente en el esfuerzo a flexión en el pie del diente, se verifica que estos esfuerzos disminuyen conforme aumenta la asimetría y corrección, para engranajes cilíndricos de dientes rectos asimétricos exteriores. Para un diente de engranaje recto con corrección X = 0; asimetría C = 1; el valor de tensión normal obtenido es de 63,02 MPa. En tanto que el mismo diente y en las mismas condiciones, pero considerando la variación de los factores geométricos corrección x = 1,25; asimetría C = 1,35; el valor de la tensión normal es de 32,22 MPa. Habiendo una reducción del valor del esfuerzo en un 48,87 %.
Tabla 4 Valores del esfuerzo en el pie del diente (MPa) en función de la corrección y asimetría
| Esfuerzo en el pie del diente (Mpa) vs corrección y asimetría | |||||
|---|---|---|---|---|---|
| X (Corrección) | C (Asimetría) | ||||
| 1 | 1,125 | 1,175 | 1,25 | 1,35 | |
| 0,00 | 63,017921 | 60,017653 | 58,896080 | 57,290213 | 55,280567 |
| 0,25 | 59,279785 | 54,402215 | 52,801727 | 50,691532 | 48,318773 |
| 0,50 | 48,578039 | 45,292694 | 44,099758 | 42,423754 | 40,377781 |
| 0,90 | 39,577098 | 37,220441 | 36,354638 | 35,129014 | 33,618045 |
| 1,25 | 37,724127 | 35,553502 | 34,753642 | 33,619149 | 32,216939 |
En la figura 4 se muestra como varían las tensiones normales en el eje z (σz) en MPa a lo largo del diente con un ángulo del perfil de 20 grados y con corrección X = 0,50 (a) y con coeficiente de asimetría de 1,35 y corrección X = 0,50 (b)
En la figura 5, se muestra como varía las tensiones normales en el eje Z en función del coeficiente de asimetría y de la corrección para un ángulo de ataque de 20o, lo que permite apreciar que la curva correspondiente a corrección x = 1,25 y asimetría C = 1, 35 presenta el menor valor de tensiones normales.
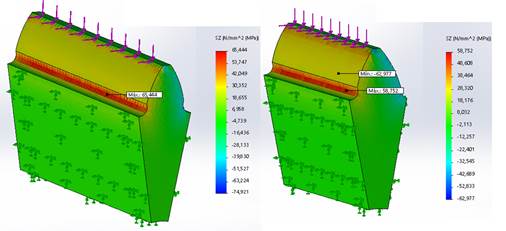
Fig. 4 Tensiones normales en el eje Z para ángulo del perfil del diente de 20° para dientes simétricos con corrección X=0,50 (a) y Z para perfil del diente asimétrico C = 1,35 y corrección X = 0,50 (b)

Fig. 5 Variación de las tensiones normales en el eje Z en función del coeficiente de asimetría y de la corrección para un ángulo del perfil del diente en la zona de ataque de 20o
En la figura 6 se muestra como varían las tensiones normales en el eje Z en función de la corrección para un ángulo de ataque de 20o, lo que permite apreciar que la curva correspondiente a asimetría C = 1, 35 y X = 1,25 presenta el menor valor de tensiones normales.

Fig. 6 Variación de las tensiones normales en el eje Z en función de la corrección y del coeficiente de asimetría para un ángulo del perfil del diente en la zona de ataque de 20o
En la tabla 5 se muestran los valores del índice de robustez a flexión el pie del diente para evaluar la influencia de los factores geométricos corrección y asimetría según la ecuación 1.
Dichos factores geométricos influyen significativamente en el índice de robustez a flexión en el pie del diente, se verifica que estos índices aumentan conforme aumenta la asimetría y corrección, para engranajes cilíndricos de dientes rectos asimétricos exteriores. Para un diente de engranaje recto con corrección X = 0; asimetría C = 1; el valor de índice de robustez a flexión obtenido es de 1. En tanto que el mismo diente y en las mismas condiciones, pero considerando la variación de los factores geométricos corrección X = 1,25; asimetría C = 1,35 es de 1,71. Consecuentemente el índice de robustez evalúa la influencia de la asimetría y corrección en la tensión normal del diente, a medida que la tensión disminuye el índice de robustez aumenta. Por lo tanto, se puede evaluar un índice de robustez a la fractura para asimetría, otro para corrección y finalmente para la combinación de ambas. Por tanto, el índice de robustez establece la robustez del diente respecto de la fractura.
Tabla 5 Valores del índice de robustez a flexión en el pie del diente en función de la asimetría y corrección
| Indice de robustez vs corrección para diferentes asimetrías | |||||
|---|---|---|---|---|---|
| X (Corrección) | C (AsimetrÍa) | ||||
| 1 | 1,125 | 1,175 | 1,25 | 1,35 | |
| 0,00 | 1 | 1 | 1 | 1 | 1 |
| 0,25 | 1,0630592 | 1,10322076 | 1,11541958 | 1,13017324 | 1,14408052 |
| 0,50 | 1,29725123 | 1,32510672 | 1,33551935 | 1,35042771 | 1,36908383 |
| 0,90 | 1,59228251 | 1,61249172 | 1,62004309 | 1,63085172 | 1,64437185 |
| 1,25 | 1,67049382 | 1,68809399 | 1,69467361 | 1,70409468 | 1,71588514 |
En la figura 7, como resultado de los valores determinados del índice de robustez en el pie del diente, se muestra como varía este índice en función de la asimetría para un ángulo de ataque de 20o, lo que permite apreciar que la curva correspondiente a corrección X = 1,25 y una asimetría C = 1,35 presenta el mayor valor de índice de robustez. Combinando estos dos principios: la asimetría y la corrección, se puede aumentar considerablemente el índice de robustez de las transmisiones por engranajes, aumentando la resistencia a la fractura, en las condiciones de operación establecidas.
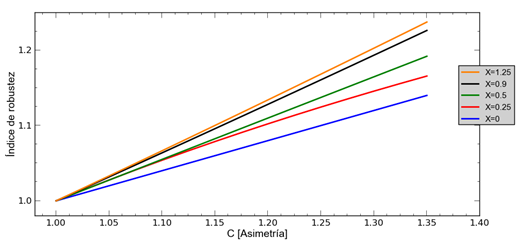
Fig. 7 Variación del índice de robustez en el eje Z en función del coeficiente de asimetría y corrección para un ángulo del perfil del diente en la zona de ataque de 20o
Con el objetivo de analizar la influencia combinada de la asimetría y corrección en el comportamiento del índice de robustez en los dientes rectos de engranajes cilíndricos exteriores de acero AISI 1045, se obtuvo la ecuación de regresión, se utilizó el del Software Curve Expert 1.6.5* para Windows,figura 8.
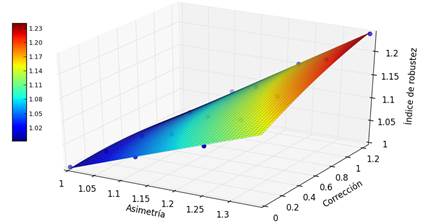
Fig. 8 Variación del índice de robustez en el eje Z en función del coeficiente de asimetría y de la corrección para un ángulo del perfil del diente en la zona de ataque de 20o
El índice de robustez se puede calcular entonces por la siguiente expresión:
Para
De los cálculos obtenidos y con la ecuación formulada se construye la Tabla 7 que muestra los valores del índice de robustez a flexión en el pie del diente para dientes asimétricos rectos exteriores para combinaciones de asimetría y corrección. Estos resultados ratifican la influencia de los parámetros geométricos en la robustez del diente, y en particular de la combinación de asimetría y corrección.
Tabla 7 Valores del índice de robustez en el pie del diente para dientes asimétricos rectos exteriores
| Índice de robustez vsasimetría para diferentes valores de corrección | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| C | X | ||||||||||
| 0 | 0,25 | 0,35 | 0,45 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 | 1,25 | |
| 1,0000 | 0,9977 | 1,0026 | 1,0037 | 1,0044 | 1,0045 | 1,0045 | 1,0039 | 1,0029 | 1,0014 | 0,9994 | 0,9924 |
| 1,0250 | 1,0083 | 1,0147 | 1,0164 | 1,0176 | 1,0180 | 1,0185 | 1,0186 | 1,0181 | 1,0172 | 1,0158 | 1,0160 |
| 1,0500 | 1,0189 | 1,0267 | 1,0290 | 1,0308 | 1,0315 | 1,0326 | 1,0332 | 1,0334 | 1,0330 | 1,0322 | 1,0320 |
| 1,0750 | 1,0295 | 1,0387 | 1,0416 | 1,0440 | 1,0450 | 1,0466 | 1,0478 | 1,0486 | 1,0488 | 1,0486 | 1,0484 |
| 1,1000 | 1,0400 | 1,0507 | 1,0541 | 1,0571 | 1,0584 | 1,0607 | 1,0624 | 1,0637 | 1,0646 | 1,0649 | 1,0649 |
| 1,1250 | 1,0505 | 1,0627 | 1,0667 | 1,0702 | 1,0718 | 1,0747 | 1,0770 | 1,0789 | 1,0803 | 1,0812 | 1,0816 |
| 1,1500 | 1,0610 | 1,0746 | 1,0792 | 1,0833 | 1,0852 | 1,0886 | 1,0916 | 1,0940 | 1,0960 | 1,0975 | 1,0984 |
| 1,1750 | 1,0715 | 1,0865 | 1,0917 | 1,0964 | 1,0986 | 1,1026 | 1,1061 | 1,1091 | 1,1117 | 1,1138 | 1,1154 |
| 1,2000 | 1,0819 | 1,0984 | 1,1042 | 1,1095 | 1,1119 | 1,1165 | 1,1206 | 1,1242 | 1,1274 | 1,1300 | 1,1325 |
| 1,2250 | 1,0923 | 1,1103 | 1,1166 | 1,1225 | 1,1253 | 1,1304 | 1,1351 | 1,1393 | 1,1430 | 1,1463 | 1,1498 |
| 1,2500 | 1,1027 | 1,1221 | 1,1291 | 1,1355 | 1,1386 | 1,1443 | 1,1496 | 1,1543 | 1,1586 | 1,1625 | 1,1673 |
| 1,2750 | 1,1131 | 1,1340 | 1,1415 | 1,1485 | 1,1518 | 1,1582 | 1,1640 | 1,1694 | 1,1742 | 1,1786 | 1,1850 |
| 1,3000 | 1,1235 | 1,1458 | 1,1539 | 1,1615 | 1,1651 | 1,1720 | 1,1784 | 1,1843 | 1,1898 | 1,1948 | 1,2028 |
| 1,3250 | 1,1338 | 1,1576 | 1,1662 | 1,1744 | 1,1783 | 1,1858 | 1,1928 | 1,1993 | 1,2054 | 1,2109 | 1,2208 |
| 1,3500 | 1,1441 | 1,1693 | 1,1786 | 1,1873 | 1,1915 | 1,1996 | 1,2072 | 1,2143 | 1,2209 | 1,2271 | 1,2389 |
Conclusiones
Se estableció un nuevo concepto para evaluar la resistencia a la fractura de los engranajes cilíndricos de dientes rectos asimétricos denominado Índice de Robustez a la Fractura y se analizó la influencia de la corrección y de la asimetría del diente en este índice. Para lograr tal fin se utilizó el diseño de experimentos y el Método de los elementos finitos, estableciéndose una expresión matemática para calcular el Índice de Robustez a la fractura en función de la corrección y la asimetría. Se concluye que el diente asimétrico y corregido tiene menos tensión normal en el pie del diente que uno simétrico y sin corregir, por tanto, para una potencia dada de diseño, el diente asimétrico corregido admite más variación en la carga aplicada o en la potencia que uno simétrico sin corregir, lográndose hasta un 48 % de aumento de la resistencia a la fractura