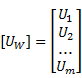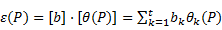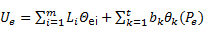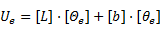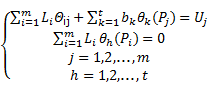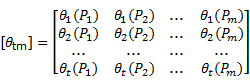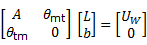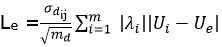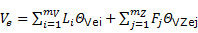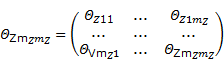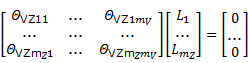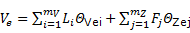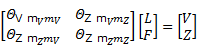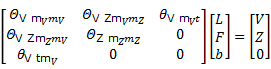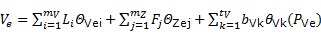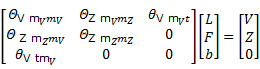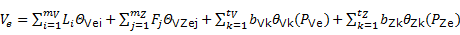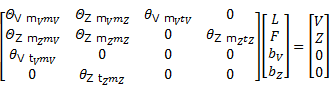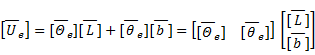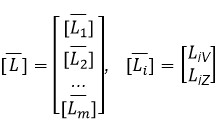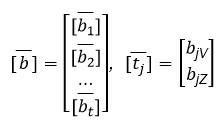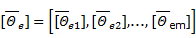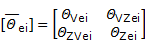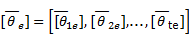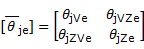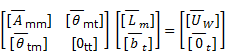Custom services
Spanish (pdf)
Article in xml format
Article references
Send this article by e-mail
Cited by SciELO 
Similars in
SciELO 
Permalink
INTRODUCCIÓN
En las geociencias, frecuentemente se presenta la necesidad de obtener modelos en escenarios n-dimensionales (n>1) que permitan explicar el comportamiento de una variable U en un dominio fenomenológico complejo de la realidad objetiva y, en consecuencia, pronosticar su comportamiento bajo ciertas condiciones prefijadas. Ejemplos de estos modelos son los siguientes:
Comportamiento espacial de la concentración de elementos químicos en un depósito de mineral
Comportamiento espacio-temporal del nivel del manto freático en una región
Comportamiento de la altura o cota topográfica en una región
Comportamiento de la velocidad promedio del viento a 10 m de altura en una región bidimensional.
Una de las maneras más conocidas para obtener exitosamente estos modelos explicativos-pronosticadores es mediante estimadores puntuales, cuyo planteamiento se describe de la forma siguiente:
Sean los m datos:
(1)
El propósito de los estimadores puntuales es obtener una aproximación del valor de U en un punto 
, o sea: hallar
.
En el presente trabajo se hace referencia a los estimadores puntuales denominados (A,U,Θ) que tienen dos formas equivalentes de expresarse (Legrá-Lobaina 2017). Sin perder generalidad en lo que sigue se explicará la forma UΘ.
Sean las matrices:
(2)
Asumiendo que esta matriz 
y su transpuesta 
tienen inversas.
(3)
(4)
Donde la función real Θ, que describe algún tipo de comportamiento de U, puede operar sobre dos puntos en la forma Θij=ξ(Pi;Pj) o puede operar sobre un punto y una función en la forma Θij=ψi(Pj).
Una aclaración necesaria es que en lo que sigue el producto escalar (denotado •) de dos vectores filas, de dos vectores columnas e incluso de un vector fila por un vector columna o viceversa, se calcula como la suma de todos los resultados que se obtienen al multiplicar dos a dos los elementos de igual índice de cada vector. El producto entre matrices o entre matrices y vectores se realiza de la forma usual.
Del estimador (A,U,Θ) debe establecerse un elemento más denominado Deriva. Esta puede escribirse como el producto escalar usual del vector 
, y un vector de t funciones conocidas:
.
(5)
La estimación se obtiene mediante la expresión:
(6)
Asumiendo el vector 
entonces (6) se escribe en notación vectorial:
(7)
Asumiendo que 
se completa el sistema de ecuaciones lineales (8), el cual debe resolverse para obtener los valores de los coeficientes Li y bk.
(8)
Donde:
(9)
La expresión (8) se escribe matricialmente:
(10)
Para determinar el error de cada estimación puntal (Pe;Ue) se puede utilizar la expresión que propone Legrá-Lobaina (2018):
(11)
En el trabajo citado se explica cómo calcular 
y
.
En las geociencias también se plantea frecuentemente la necesidad de trabajar con modelos multivariados, tal como lo explican algunos investigadores (Chilés y Delfiner 1999; Díaz-Viera 2002; Rivoirard 2003; Giraldo 2005). Ejemplos de estos casos para las ciencias eólicas son los siguientes:
Comportamiento interrelacionado de la cota topográfica y de la velocidad promedio del viento a 10 m de altura en una región
Comportamiento de los parámetros K y C de una Distribución de Weibull que modela estadísticamente la velocidad del viento.
El objetivo del presente trabajo es explicar e ilustrar, mediante dos casos de estudio de las geociencias, tres metodologías fundamentales de los estimadores (A,U,Θ) cuando se trata de considerar dos o más variables dependientes y dos o más variables independientes.
METODOLOGÍA BASADA EN EL USO DE DERIVA PARA MODELAR V CONSIDERANDO EL COMPORTAMIENTO DE Z
Sea una región bidimensional donde se tienen las variables espaciales independientes X e Y que denotan las coordenadas de cada punto, se tienen las coordenadas de m=36 puntos Pi=(xi;yi) (i=1,…,36).
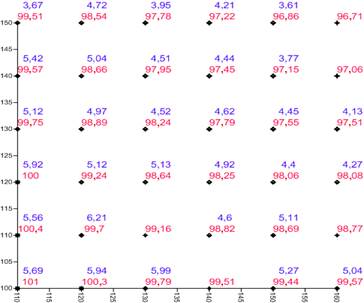
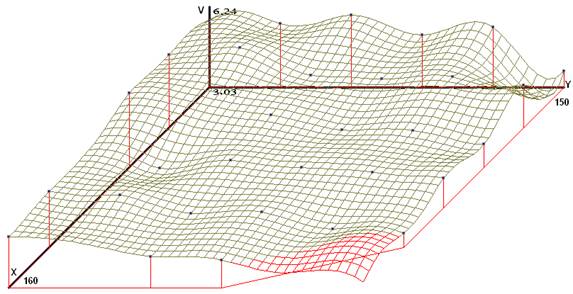
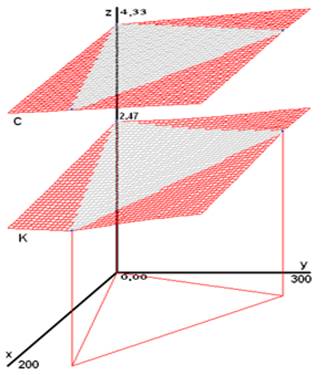
Fig. 1 Datos de las variables V (velocidad media del viento, superior en azul) y Z (altura topográfica, inferior en rojo).
Según la figura 1, en 31 de los puntos se conoce la velocidad media del viento, denotada V, y en los 36 puntos se conoce la altura topográfica con respecto al nivel del mar, que se denota Z. Se denominará al escenario caso de estudio 1 y, en este caso, al conjunto de datos se le denota:
Hipotéticamente, se pueden hacer las consideraciones siguientes:
V es una variable que depende espacialmente de P y su medición es compleja y costosa. Esta aseveración implica que V es una variable candidata a ser estimada en cualquier punto Pe.
Z es una variable que también depende espacialmente de P y su medición es sencilla y económica por lo que esta variable puede conocerse por mediciones en el punto Pe. No se puede descartar que el valor Ze(Pe) puede ser estimado mediante un modelo externo al proceso de estimación de V.
Entre V y Z existe cierta interdependencia compleja que puede reducirse a que: “la altura Z influye en el valor de la velocidad V”. El modelo formal de esta interdependencia es desconocido.
En este caso, se tiene la posibilidad de adaptar el modelo descrito en la Introducción del artículo tomando las definiciones siguientes:
m=31, ya que se omiten los puntos de W donde faltan datos.
t=2;
; 
. De esta manera se obtiene:
>.Modelo UPD con potencia p=1,45; donde se asume la distancia euclidiana y factor de suavización nulo (Legrá-Lobaina 2018).
Para lograr cierta autenticidad para el caso de estudio 1 que se analiza, en el presente trabajo se ha establecido que:
Donde DE es la desviación estándar de los datos Zi y RP es para cada P un número aleatorio en el intervalo 
; entonces véase que el valor del producto 2 DE RP siempre estará entre el intervalo 
.
El lector puede notar que la función Z(P) pudiera tomarse de otras maneras. Por ejemplo: también multiplicar Zi por 2 DE RP o solo multiplicar Zi por 2 DE RP o no multiplicar por este factor.
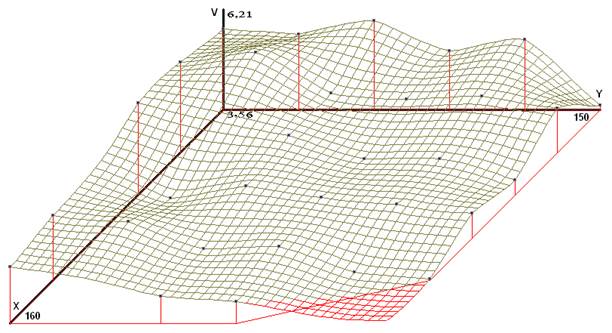
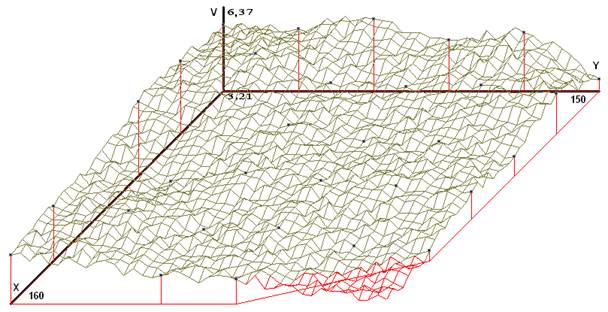
Para comparar a continuación se muestran gráficamente los modelos UPD para 
(Fig. 2) y 
(Fig. 3), donde para cada malla se han definido dimensiones 40×40 puntos en los límites geométricos de los puntos Pi y para cada estimación puntual del segundo modelo; el valor de 2 DE RP es aleatorio.
El comentario obvio es que el segundo modelo refleja de manera clara la influencia de Z sobre V. Este enfoque es conveniente en la medida en que los valores de Z(P) tengan alta exactitud.
Por otra parte, si en cada oportunidad en que se obtenga un modelo multivariado se toman valores aleatorios de RP, eventualmente diferentes, entonces cada modelo multivariado constituye una simulación del modelo univariado
METODOLOGÍA BASADA EN LA INTERDEPENDENCIA PARA MODELAR V CONSIDERANDO EL COMPORTAMIENTO DE Z
En esta oportunidad los datos del caso de estudio 1 se asumen como dos conjuntos donde sus cardinales y coordenadas pueden ser diferentes:
También se suponen conocidas las funciones:
ΘV que describe el comportamiento de U
ΘZ que describe el comportamiento de Z
ΘVZ que define el comportamiento conjunto de V y de Z.
Se verá primero el caso de la Estimación de V usando las funciones ΘU, ΘZ y ΘVZ y asumiendo particularmente que no hay deriva. Se propone:
(12)
En esta ocasión solo se hará referencia al caso en que Θij=ξ(Pi;Pj) y además debe notarse que:
En la última expresión se tiene que, en general: ΘVZij ≠ ΘVZji.
Asumiendo que: 
y 
Siguiendo las ideas de Legrá-Lobaina (2017), para obtener los vectores 
y 
debe resolverse el sistema:
(13)
Donde se ha considerado además que:
(14)
(15)
(16)
(17)
Las ecuaciones de las secciones 
y 
se construyen a partir de asumir y combinar las condiciones:
(18)
(19)
En el caso en que no existe o se desconoce ΘVZij, el estimador (12) se puede escribir como:
(20)
Y el sistema (13) se escribe:
(21)
Si existe deriva 
para V y no existe para Z, el estimador (12) se rescribe:
(22)
Donde: 
y 
.
Asumiendo que: 
entonces se obtiene que:
Y el sistema (13) queda finalmente:
(23)
De manera semejante las expresiones (20) y (21) pueden generalizarse cuando se considera la deriva de V:
(24)
(25)
Finalmente puede analizarse el caso en que también existe deriva independiente para Z denominada
. La nueva generalización será ilustrada en este texto para las expresiones (22) y (23) pero de manera semejante pueden rescribirse (24) y (25). El estimador queda:
(26)
Donde: 
y
.
Asumiendo, además, que 
y que para todo punto P Vi , i=1,…,mV se cumple que 
. Entonces se obtiene el sistema (27) que permite obtener los valores de 
, 
, 
y 
.
(27)
Estos modelos pueden generalizarse aún más de otras maneras (Chilés y Delfiner 1999; Díaz-Viera 2002; Rivoirard 2003; Giraldo 2005):
Aumentando el número de variables dependientes auxiliares.
Considerando otras formas o influencias de la deriva.
Estimando simultáneamente diversas variables dependientes. Esta generalización se describe en el próximo epígrafe.
A continuación se muestra el modelo de malla obtenido al aplicar este enfoque a los datos del caso de estudio 1, asumiendo que:
mV = 31 y mZ = 36.
El modelo descrito por las expresiones (22) y (23).
Las funciones ΘZij, ΘVij y ΘVZij se tomarán como Funciones de Base Radial del tipo Spline Cúbico Natural:
. Para los puntos de WV se usa ΘV y RV=6,45; para de WZ se usa ΘZ y RVZ=5,56; y para los de WV y WZ se usa ΘVZ y RVZ=5,97. La distancia d es la euclidiana con factor de suavización nulo.Deriva
(Fig. 4) y no hay deriva respecto a Z.
METODOLOGÍA BASADA EN LA ESTIMACIÓN SIMULTÁNEA DE DOS VARIABLES DEPENDIENTES
La forma dual ΘU de estas variantes son muy conocidas (Myers 1992; Rusu y Rusu 2006) y usadas en la Geoestadística bajo la denominación de Co-Kriging (Chilés y Delfiner 1999; Díaz-Viera 2002; Rivoirard 2003; Giraldo 2005; Marcotte 2018) donde las funciones ΘZ, ΘV son los correspondientes variogramas (o covarianzas) y ΘVZ es el variograma cruzado (o covarianza cruzada) entre V y Z; debe señalarse que en este enfoque tienen especial importancia los conceptos de insesgamiento, la varianza de estimación y la optimización (minimización) de esta.
Todos los trabajos citados describen alguna forma matricial de estos estimadores ΘU. Siguiendo ese enfoque a continuación se describe la forma matricial general de los estimadores UΘ para el caso de que:
Los valores de todas las variables dependientes se conocen en m coordenadas Pi.
Se presenta una función Θ como una matriz cuadrada del orden de la cantidad de funciones dependientes a modelar.
Se presenta una deriva generalizada de t componentes expresada matricialmente.
El estimador (7) ahora se escribe como:
(28)
Donde, sin perder generalidad, los vectores que aparecen en esa expresión para dos variables independientes V y Z se escriben:
(29)
(30)
(31)
,
(32)
,
(33)
Para determinar los elementos de los vectores 
y 
debe ser resuelto el sistema matricial:
(34)
Donde:
(35)
Y como es usual se asume que: 
Puede notarse que es esencial establecer, además de los datos, todas las funciones del tipo: 
que garanticen que el sistema (34) tenga solución única.
Dado que el producto entre matrices no es conmutativo entonces el estimador (28) es solo posible efectuarlo en el orden que se ha descrito. Para determinar el modelo dual UΘ deberá tenerse en cuenta la regla formal para hallar la transpuesta de una matriz de matrices: 
y la regla: 
, donde M1, M2 y M3 son matrices de órdenes que permitan esos productos.
Para ilustrar el enfoque descrito por (28) y (34) se explicará una modelación del siguiente caso de estudio 2:
Sean tres puntos del espacio R2 donde se conocen sus coordenadas y los valores de K y C denominados, respectivamente, Factor de Forma y Factor de Escala de la Distribución de Weibull (tabla 1), tal como señalan Terrero-Matos, Legrá-Lobaina y Lamorú-Reyes (2017), que describen la distribución de frecuencias de la velocidad del viento en cada punto a 10 m de altura.
Tabla 1 Datos de los parámetros K y C de los modelos de Weybull para tres puntos de una región plana
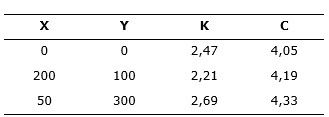
Se quieren establecer modelos de K y C en la región plana que contienen los tres puntos de los datos, de manera que se disponga de un modelo del potencial eólico a 10 m de altura. En esta oportunidad se hacen las consideraciones siguientes:
El modelo resultante se escribe formalmente:
Estos modelos se muestran en la figura 5.
y
.
Finalmente debe comentarse sobre la posibilidad de generalizar también la expresión (11) para tener disponible una vía para aproximar los errores de una estimación multivariada puntual.
Como se ha explicado antes (Legrá-Lobaina 2018) en la estimación univariada el vector / se obtiene en el contexto del enfoque dual ΘU. Para el estimador multivariado este vector se define:
,
(36)
Teniendo en cuenta (29) y (36) los errores de una estimación simultánea de dos variables se escriben:
(37)
CONCLUSIONES
Las tres metodologías descritas generalizan a los estimadores multivariados (A,U,Θ) los cuales, desde el enfoque de considerar las relaciones entre dos o más variables dependientes, dan respuestas a un amplio conjunto de problemas de modelación en las geociencias. Es significativo que todos los estimadores (A,U,Θ) pueden ser considerados admisibles en esta generalización multivariable y la expresión para aproximar el error de estimación también es extendida.
El estimador simultáneo de variables dependientes explicado constituye una sistémica y poderosa opción para la modelación múltiple; el enfoque algebraico que aquí se presenta lo convierte en una herramienta matemática de fácil programación en aplicaciones como MatLab o en desarrolladores clásicos como C++, Visual Basic o Delphi, lo cual ha permitido modelar los dos casos de estudio presentados.
