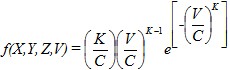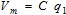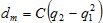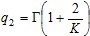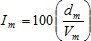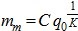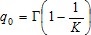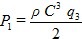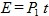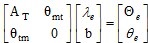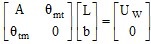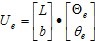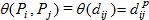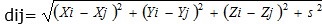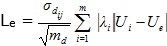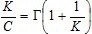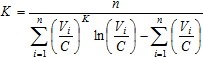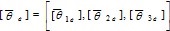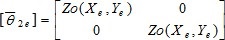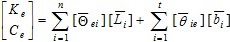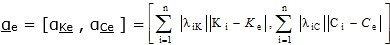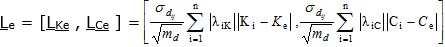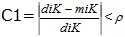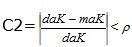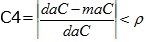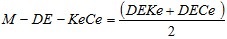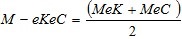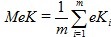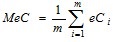Artículo Original

Estimación por método UPD multivariable de un modelo óptimo 3D de recursos eoloenergéticos

Estimation by multivariable UPD method of an optimal 3D model of wind energy resources

0000-0002-0686-3566Eduardo Terreo-Matos^{1  *}  , 0000-0002-4793-4754Arístides A. Legrá-Lobaina¹ 

¹Universidad de Moa, Holguín, Cuba.

RESUMEN

A fin de evaluar los recursos eoloenergéticos de una región promisoria este trabajo propone un estimador UPD multivariado, miembro de la familia (A,U,Θ) con parámetros p y s, que permitió calcular simultáneamente los parámetros de Weibull K y C en un punto P _e , a partir de los valores medidos de estas variables en varios puntos de muestreo. Durante la estimación 3D se tuvo en cuenta la relación espacial entre los datos y los valores asociados de altura y rugosidad del terreno; con los resultados estimados se elaboró un modelo de recursos energéticos del viento dado por una malla 3D donde a cada nodo se asociaron los valores de K y C. Finalmente, se describe un método de optimización combinatoria para encontrar los valores de p y s tal que el modelo de malla sea factible y óptimo para los datos dados.

Palabras-clave: estimador UPD; energía eólica; modelos matemáticos; malla 3D; optimización combinatoria

ABSTRACT

This paper presents a multivariate UPD estimator, family member (A,U,Θ) with parameters p and s, which allows to calculate simultaneously parameters of Weibull K and C at a point P _e from the measured values of these variables in several sampling points. During the 3D estimation, the spatial relationship between the data and the associated values of elevation and roughness of the terrain is taken into account; with the estimated results, a model of wind energy resources is developed, given by a 3D mesh where to each node is associated the values of K and C. Finally, a method of combinatory optimization is described to find the values of p and s such that the mesh model is feasible and optimal for the given data.

Key words: UPD estimator; wind energy; mathematical models; 3D mesh; combinatory optimization

INTRODUCCIÓN

La eoloenergética puede considerarse una disciplina tecnológica que surge del estudio del potencial energético de los vientos y es extensión práctica de los estudios geofísicos de estos. Para aprovechar los recursos eoloenergéticos de una región promisoria R es necesario que estos estén previamente caracterizados para poder decidir si existe la tecnología que haga viable y económicamente factible su explotación.

En el presente trabajo se asume que un modelo de recursos eólicos es esencialmente una red M o malla tridimensional de m puntos (denominados nodos) del espacio Pi=(Xi,Yi,Zi), i=1,…,m situados de manera regular por encima de la superficie de la región R, donde a cada punto se le asocian valores relacionados con la velocidad V del viento, así como con la potencia y energía que este viento genera.

Según ^{Feitosa y demás investigadores (2002}), para identificar el recurso eoloenergético en un punto es usual obtener en P _i de M una distribución de Weybull caracterizada por K (parámetro denominado factor de forma, adimensional) y C (factor de escala, m/s).

Para ^{Moreno y el colectivo de autores (2017}) es práctica común que mediante torres, con sistemas automatizados múltiples para medir la velocidad y dirección del viento a varias alturas, se obtengan los valores de V en cada uno de los n puntos Pj durante al menos dos años y, a partir de estos datos, determinar una distribución de frecuencia de V para un año tipo en cada punto y se ajusta a ella una función de densidad de una Distribución de Weibull, tal como se explica en ^{Serrano (2013}), ^{Terrero-Matos, Legrá-Lobaina y Lamorú-Reyes (2014}).

La distribución de Weibull tiene la expresión siguiente:

(1)

A partir de K y C pueden determinarse para las coordenadas del punto P=(X,Y,Z) varios elementos esenciales del contexto eoloenergético:

Velocidad media del viento (Vme):

(m/s) (2)

Donde; es la función Gamma

Desviación estándar del viento (Vde):

(m/s) (3)

Donde

Intensidad de la turbulencia del viento (InT):

(Porcentual) (4)

Moda de la velocidad del viento (Vmo):

(m/s) (5)

Donde

Velocidad donde se obtiene la máxima potencia del viento (VMP):

(m/s) (6)

Densidad de potencia (DPo):

() (7)

Donde es la densidad del aire en kg/m3.

Energía por m2 en un intervalo de tiempo (EAT)

(Ws/m) (8)

Donde t(s) es el tiempo considerado para el cálculo.

Nótese que si se conoce K y C en cada punto P _i de la malla M se pudiera caracterizar la energía del viento en ese punto si se dispusiera de anemómetros en cada punto P _i . Dado que es económicamente impracticable poder medir el viento en cada punto P _i de M se hace necesario proponer una vía alternativa para, a partir del conocimiento de K y C en unos pocos puntos donde se colocaron las torres de medición con sus anemómetros, obtener los valores de K y C (o de Vm) para todos los puntos de la malla M.

Diversos enfoques han sido considerados por algunos autores para obtener modelos 2D y 3D de los citados parámetros. Entre los más recientes aparecen: ^{Agnese-Ramos (2017}); ^{Artillo-García (2017}); ^{Arenas-López (2018}) y ^{Ibargüengoytia-González et al. (2018}). Una exhaustiva revisión sobre el tema presenta ^{Roque (2019}), donde los más eficaces modelos están relacionados con altas complejidades de cálculo y no se describen explícitamente procesos de optimización que dependan de los datos disponibles y de los escenarios topográficos y de rugosidad del terreno.

Siguiendo los desarrollos de ^{Legrá-Lobaina (2017}, ²⁰¹⁸) y de ^{Legrá-Lobaina y Terrero-Matos (2019)}, el presente trabajo tiene como objetivo presentar un método UPD, de la familia (A,U,Θ), multivariable y óptimo, para estimar un modelo 3D de recursos eoloenergéticos en una región promisoria.

DEFINICIONES PRELIMINARES

Modelo de topografía

Se trata de un modelo matemático (puede ser una tabla, ecuaciones o un procedimiento) que permite encontrar la cota Zo (altura topográfica del terreno) para cualquier coordenada (X,Y) de una región plana.

Modelo de rugosidad

Es un modelo matemático (tabla, ecuaciones o procedimiento) que permite encontrar el valor de la rugosidad R (^{Terrero-Matos, Legrá-Lobaina y Lamorú-Reyes 2014}) para cualquier coordenada (X,Y) de una región plana.

Mediciones de la velocidad del viento

Se tienen n puntos P _j =(X _j ,Y _j ,Z _j ), j=1,…,n, donde se realizaron mediciones de V mediante anemómetros durante cierto período de tiempo y, por tanto, en esos puntos se determinaron K_j y C_j. Al conjunto de mediciones se le denomina D.

Se asume que X_j (en metros) es la coordenada este a oeste; Y_j (en metros) es la coordenada Sur a Norte; Z _j es (en metros) la coordenada de la altura relativa del anemómetro a partir del nivel del terreno.

También se asocian a cada punto P _j los valores de Zo _j que es la cota o altura de la superficie del terreno sobre el nivel del mar en las coordenadas (X _j ,Y _j ) y R _j es el valor de la rugosidad en ese punto.

Modelo de recursos eoloenergéticos (Malla M)

La malla M tiene m puntos de coordenadas relativas P _i =(X _i ,Y _i ,Z _i ) y, además, cada punto tiene asociados los valores Zo y R obtenidos en los modelos descritos en 2.1 y 2.2, respectivamente. El modelo de recursos se completa con los valores estimados de K y C y los valores calculados de Vm (ecuación 2), dm (ecuación 3), P ₁ (ecuación 7) y E (ecuación 8).

Estimadores (A,U,Θ) univariados disponibles

La familia de estimadores unidimensionales (A,U,Θ) con deriva se describe en el trabajo de ^{Legrá-Lobaina (2017}). A la expresión Θ se le denomina función núcleo del estimador; la matriz A y los vectores se determinan a partir de los datos.

Para los métodos de la clase ΘU se resuelve el sistema para obtener el vector de ponderadores :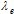

(9)

Y se estima el valor de U_e mediante la expresión:

)(10

Para los métodos (equivalentes) de la clase UΘ se resuelve el sistema siguiente para obtener el vector de ponderadores L:

(11)

Y se estima el valor de U_e mediante la expresión:

(12)

Entre los diversos métodos UΘ se encuentra el método UPD (^{Legrá-Lobaina, Lamorú-Reyes y Cala-Hinojosa 2016}) que toma su nombre del hecho de que la función Θ está dada por una potencia de la distancia euclidiana (PD), es decir:

(13)

Donde para dos puntos P_i=(X_i,Y_i,Z_i) y P_j=(X_j,Y_j,Z_j) se calcula la distancia euclidiana suavizada con el factor s mediante la expresión:

(14)

En el trabajo de ^{Legrá-Lobaina (2018}) se presentan fórmulas para evaluar el error de estimación de cualquier método (A,U,Θ) mediante dos expresiones dadas en notación de la clase ΘU:

Error si solo se considera la relación entre los valores estimados con respecto a los datos:

(15)

Error si, además, se consideran las escalas de las coordenadas:

(16)

Donde 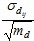es el error estándar de las medias (^{Miller, Freund y Johnson 2005}) de las distancias.

Estimadores (A,U,Θ) multivariados

Las relaciones entre K y C son muy complejas, tal como señala ^{Jaramillo-Salgado (2013}):

(17)

y como describen ^{Valdés y Vinagre (2012}):

(18)

(19)

Esta relación, implícita y no lineal, debe ser considerada por cualquier estimador que se evalúe en esta investigación. Es por ello que se propone un estimador que determine simultáneamente los valores de K y C y esta es la razón por la cual se le cataloga como multivariado.

METODOLOGÍA

Como se explica más adelante, en este trabajo se integran dos enfoques metodológicos (^{Legrá-Lobaina y Terrero-Matos 2019}) para realizar estimaciones multivariables teniendo en cuenta la presencia de dos o más variables dependientes. Estos enfoques son:

1. Metodología para modelar una variable dependiente U ₁ considerando en la deriva el comportamiento de otra variable dependiente U ₂ de la cual es posible conocer previamente sus valores para el punto P_e donde se quiere estimar el valor de U ₁ .

2. Metodología para la estimación simultánea de dos variables dependientes U ₁ y U ₂ atendiendo a la forma matricial de los estimadores (A,U,Θ).

RESULTADOS Y DISCUSIÓN

Método de estimación que se propone

Para estimar K y C simultáneamente en un punto de coordenadas P _i =(X _i ,Y _i ,Z _i ) a partir de los n datos D tal que se considere la posible interrelación ente K y C y que, además, en la estimación influyan decisivamente los valores de Zo y R, se proponen las pautas siguientes:

La función núcleo, que permite obtener la matriz A y realizar las estimaciones puntuales, tiene la forma:

)(20

Donde d _ji es la distancia euclidiana (con factor de suavización s escogido por el investigador) entre el punto P _i de coordenadas (X _i ,Y _i ,Z _i ) y el punto P _j con las coordenadas (X _j ,Y _j ,Z _j ). En particular d _ei es la distancia entre P _i y el punto donde se estima P _e =(X _e ,Y _e ,Z _e ).

El parámetro p es la potencia del modelo UPD que para este caso es un valor mayor que cero seleccionado por el investigador.

Dado que el coeficiente de variación de una variable se calcula como el cociente de la desviación estándar de sus valores entre la media aritmética de estos (^{Miller, Freund y Johnson 2005}), entonces:

• V _k es el coeficiente de variación de la variable K en los datos.

• V _c es el coeficiente de variación de la variable C en los datos.

• V _kc es la variación conjunta de las variables K y C caracterizada como la covarianza entre K y C (^{Miller, Freund y Johnson 2005}) dividida por el producto de las medias aritméticas de K y C.

La deriva es de orden t=3 y tendrá la forma:

(21)

Donde:

Los cálculos de las dos últimas expresiones se realizan mediante los correspondientes modelos de topografía y rugosidad descritos más arriba.

El modelo de estimación queda entonces:

(22)

Donde: 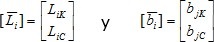, que se calculan resolviendo el sistema de ecuaciones matriciales:

(23)

Tal como explican ^{Legrá-Lobaina y Terrero-Matos (2019}).

El error de estimación para cada variable K y C se estima mediante las expresiones explicadas en el trabajo citado:

(24)

(25)

Optimización del estimador considerando dos parámetros de la función núcleo

En la función núcleo del estimador los valores de s y p deben ser seleccionados por el investigador y se propone que sean escogidos aquellos que optimicen algún índice de calidad de la estimación de la malla.

Asumamos que:

miK es el valor mínimo de los valores estimados de K en la malla

diK es el valor mínimo de los valores de K en los datos.

maK es el valor máximo de los valores estimados de K en la malla

daK es el valor máximo de los valores de K en los datos.

miC es el valor mínimo de los valores estimados de C en la malla

diC es el valor mínimo de los valores de C en los datos.

maC es el valor máximo de los valores estimados de c en la malla

daC es el valor máximo de los valores de C en los datos.

Se proponen como estimadores factibles aquellas para los valores de s y p se cumplan las condiciones 26, 27, 28 y 29:

(26)

(27)

(28)

(29)

Donde ρ≥0 es un valor que indica (en escala unitaria) el límite de diferencia entre los extremos de K y C en la malla con respecto a los extremos de K y C en los datos. En este trabajo se tomará ρ=0,05.

Entre los estimadores factibles se propone tomar como mejores aquellos donde sea mayor el valor de la media aritmética de las desviaciones estándar de las estimaciones de K y C en la malla:

(30)

Donde DeKe es la desviación estándar de los valores de estimados de K y DeCe es la desviación estándar de los valores de estimados de C.

Con fines de control de la calidad de las soluciones se debe revisar la media aritmética de los promedios de los errores de estimación:

(31)

Donde para la variable K se tiene:

(32)

eK _i es el error calculado al estimar K _e en el punto P _i

Y para la variable C se tiene:

(33)

eC _i es el error calculado al estimar C _e en el punto P _i

Debe especificarse que los errores de estimación se calcularán mediante la expresión (24), ya que en este caso las escalas de las coordenadas permanecerán invariables.

Nótese que:

• De cumplirse las condiciones (26) al (29) entonces los valores estimados obtenidos estén en el rango de los datos, o sea que la factibilidad de un estimador está determinada con el hecho de que los valores estimados de la malla estén en el rango de los datos de K y C.

• Si se cumple la condición (30) entonces se garantiza que los valores estimados no tengan un comportamiento “aplanado”, propio de los casos donde p es cercana a 0.

• Al cumplirse la condición (31) se certifica que los valores estimados de K y C son cercanos a los valores de los datos.

Para optimizar se aplica un método de búsqueda exhaustivo (^{Rivera 2004}) sobre un enfoque de optimización combinatoria (^{Blum y Oli 2003}). Para ello se propone realizar una discretización de s y p (^{Legrá-Lobaina, Lamorú-Reyes y Cala-Hinojosa 2016}).

En la práctica se toman todas las combinaciones de los valores de s y p, y se guardan todos los pares factibles, donde se cumplan las condiciones del (26) al (29).

Entre las condiciones factibles se toma como óptima aquella donde es mínima la expresión (31) y (32) tenga valores satisfactorios.

Aplicación ilustrativa del método propuesto

Sean los datos de la Tabla 1 que expresan una situación hipotética del conocimiento actual del potencial eoloenergético en una región promisoria.

Tabla 1 Datos de los parámetros K, C, Zo y R para nueve puntos de una región espacial 

X	Y	Z	K	C	Zo	R	VM
0	0	0	2,1	6	40	0,1	5,3145
0	0	20	3	7	40	0,1	6,25366
0	0	40	2,5	8	40	0,1	7,09808
400	150	0	2,4	6,3	35	0,2	5,584068
400	150	20	2,8	6,7	35	0,2	5,964206
400	150	40	3,2	7	35	0,2	6,272
100	300	0	1,9	5,8	27	0,15	5,147906
100	300	20	2,6	6	27	0,15	5,33124
100	300	40	2,8	6,5	27	0,15	5,78617

Los modelos de topografía y de rugosidad han sido obtenidos a partir de estos datos mediante ajustes mínimos cuadrados exactos:

Zo(X,Y)=40 + 0,00428571428571433 X - 0,044761904761905 Y

R(X,Y)=0,1 + 0,00021428571428571 X + (9,523809523809E-5) Y

Los modelos de la malla M que se estimarán se caracterizan por:

Variable X: Mínimo=-50 Máximo=450 Número de nodos=50

Variable Y: Mínimo=-50 Máximo=350 Número de nodos=50

Variable Z: Mínimo=0 Máximo=50 Número de nodos=10

De manera que cada malla tiene 50×50×10=25000 nodos. Debe destacarse que el 71 % de los nodos están fuera de la región convexa limitada por la frontera determinada por la proyección de los datos en el plano XY, lo cual quiere decir que solo el 29 % de las estimaciones son interpolaciones. Esta es una exigencia significativa para cualquier estimador puntual 3D.

Para obtener los correspondientes modelos de malla M 2 000 estimadores se probaron tomando las combinaciones de valores:

s: Mínimo=0 Máximo=5 Total de puntos: 40

p: Mínimo=0,01 Máximo=3 Total de puntos: 50

La función núcleo se escribe:

)(34

Los resultados obtenidos al realizar cincuenta millones de estimaciones de (K,C) indican que 893 son factibles porque cumplen con las condiciones de la (26) a la (29). En la Tabla 2 se muestran las características de los 20 estimadores factibles de menor valor de (31), entre las cuales debe ser seleccionada la óptima.

Tabla 2 Los 20 mejores resultados de los 893 factibles 

FACTOR s	POTENCIA p	M-eKeC		M-DE-KeCe
0,12820513	1,41346939	0,82403599	0,02788237	0,43679858
0,25641026	1,41346939	0,82544857	0,0280047	0,43678772
0,38461538	1,41346939	0,82715682	0,02815232	0,43677527
0,51282051	1,41346939	0,82908541	0,02831848	0,43676178
0,64102564	1,41346939	0,83119326	0,02849947	0,43674755
0,76923077	1,41346939	0,83345406	0,02869292	0,4367327
0,8974359	1,41346939	0,83584984	0,02889714	0,43671735
1,02564103	1,41346939	0,8383678	0,02911087	0,43670154
1,15384615	1,41346939	0,84099708	0,02933312	0,4366853
1,28205128	1,41346939	0,84372997	0,02956311	0,43666865
1,41025641	1,41346939	0,84656026	0,0298002	0,43665161
1,53846154	1,41346939	0,84948191	0,03004385	0,43663417
0	1,41346939	0,84062377	0,02929248	0,4366323
1,66666667	1,41346939	0,85249064	0,0302936	0,43661633
1,79487179	1,41346939	0,85558319	0,03054907	0,43659809
1,92307692	1,41346939	0,85875601	0,03080991	0,43657943
2,05128205	1,41346939	0,862006	0,03107582	0,43656035
2,17948718	1,41346939	0,86533051	0,03134656	0,43654084
2,30769231	1,41346939	0,8687273	0,03162188	0,43652089
2,43589744	1,41346939	0,87219468	0,03190158	0,43650048
2,56410256	1,41346939	0,87573142	0,03218549	0,4364796
0,12820513	1,41346939	0,82403599	0,02788237	0,43679858
0,25641026	1,41346939	0,82544857	0,0280047	0,43678772
0,38461538	1,41346939	0,82715682	0,02815232	0,43677527

A partir de los resultados de la Tabla 2 puede seleccionarse el estimador más adecuado. Proponemos elegir al de la primera posición (en rojo), donde los parámetros de su función núcleo son: s=0,12820513; p=1,41346939.

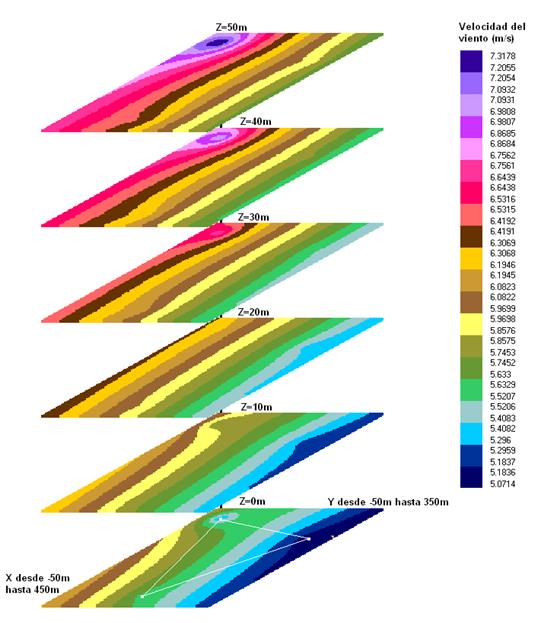
Se obtiene un modelo de malla donde entre otra vez aparecen los valores de Vm que se representa para seis valores de Z en la Figura 1, sin incluir las correcciones Zo en el dibujo de la coordenada vertical.

Figura 1 Representación 3D del modelo óptimo de Vm. 

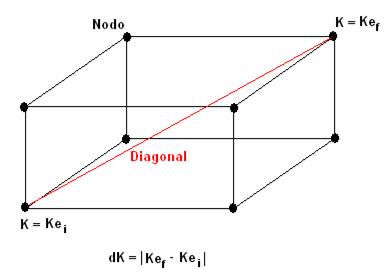
Finalmente debe ser señalado que la máxima diferencia dK entre los valores absolutos de K _e , tomados en la diagonal de una celda de la malla M, es 0,35959354669 (Figura 2) y de forma análoga para la variable C se obtiene que la máxima diferencia entre los C _e de la diagonal de una celda de M es 0,291870112525. Estos resultados vaticinan que las hipersuperficies que modelan a K y C son “suaves”, o sea, sin grandes cambios de pendientes de K y C en puntos vecinos.

Figura 2 Valor de la diferencia dK en una celda de la malla M. 

CONCLUSIONES

• Se caracteriza un estimador UPD multivariado 3D, miembro de la familia (A,U,Θ) y de parámetros p y s, que permite obtener simultáneamente los parámetros de Weibull K y C en un punto P _e , a partir de los valores medidos de estas variables en varios puntos de muestreo, teniendo en cuenta la relación espacial entre los datos y los valores asociados de altura y rugosidad del terreno.

• Se define un modelo de recursos energéticos del viento, dado por una malla 3D, donde a cada nodo se asocian valores estimados de K y C.

• Desde un enfoque de optimización combinatoria y con el método de búsqueda exhaustiva se han encontrado valores de p y s tal que el modelo de malla es factible y óptimo para los datos dados.

REFERENCIAS

Agnese-Ramos, D. 2017: Estabilidade atmosférica em projetos eólicos: estimativa bayesiana do comprimento de Monin Obukhov e simulação do escoamento atmosférico. Dissertação de Mestrado. Universidade Federal do Rio de Janeiro. Consulta: 14/02/2019. Disponible en: Disponible en: https://www.researchgate.net/publication/321635545_ESTABILIDADE_ATMOSFERICA_EM_PROJETOS_EOLICOS_ESTIMATIVA_BAYESIANA_DO_COMPRIMENTO_DE_MONIN_OBUKHOV_E_SIMULACAO_DO_ESCOAMENTO_ATMOSFERICO

Arenas-López, J. P. 2018: Modelos de velocidades de viento basados en ecuaciones diferenciales estocásticas. Tesis de maestría. Instituto Politécnico Nacional. Ciudad de México.

Artillo-García, M. 2017: Estudio del Potencial Eólico y Viabilidad de Parque Eólico en Andalucía. Trabajo de Diploma. Universidad de Sevilla. Sevilla. Consulta: 22/02/2019. Disponible en: Disponible en: https://idus.us.es/xmlui/bitstream/handle/11441/65467/TFG_Manuel%20 Artillo%20Garc%c3%ada.pdf?sequence=1&isAllowed=y

Blum, A. y Oli, R. A. 2003: Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Computing Surveys, 35(3): 268-308. Consulta: 17/02/2019. Disponible en: Disponible en: https://www.iiia.csic.es/~christian.blum/downloads/ blum_roli_2003.pdf

Feitosa, E. A. N.; Pereira, A. L.; Silva, G. R.; Veleda, D. y Silva, C. C. 2002: Panorama do potencial eólico no Brasil. Projeto BRA/00/029. Agência Nacional de Energia Elétrica. Brasília. P. 42-52.

Ibargüengoytia-González, P. H.; Reyes-Ballesteros, A.; Borunda-Pacheco, M. y García-López, U. A. 2018: Predicción de potencia eólica utilizando técnicas modernas de Inteligencia Artificial. Revista Ingeniería Investigación y Tecnología, XIX (4): 1-11. ISSN: 2594-0732. DOI. http://dx.doi.org/10.22201/fi.25940732e.2018.19n4.033

Jaramillo-Salgado, O. A. 2013: Energía eólica teoría y conceptos. En: Evento CAPEV 15 de la OLADE. Temixco, Morelos, México. Consulta: 15/02/2019. Disponible en: Disponible en: https://www.slideserve.com/delano/energ-a-e-lica-teor-a-y-conceptos .

Legrá-Lobaina, A. A. 2017: Modelos de malla basados en estimadores (A,U,Θ). Revista HOLOS, 33(4): 88-110. DOI:10.15628/holos.2017.5351.

Legrá-Lobaina, A. A. 2018: Evaluación del error en estimaciones (A,U,Θ). Revista HOLOS , 33(4): 88-110. DOI:10.15628/holos.2017.5351.

Legrá-Lobaina, A. A.; Lamorú-Reyes, A. y Cala-Hinojosa, A. 2016: Evaluación de modelos 2D de variables geotecnológicas en un bloque de un yacimiento laterítico cubano. Quinta parte: Optimización combinatoria del método UPD. Minería y Geología, 32(4): 33-48. ISSN: 1993 8012.

Legrá-Lobaina, A. A. y Terrero-Matos, E. 2019: Modelación de variables eólicas mediante estimadores (A,U,Θ) multivariados. Minería y Geología , 35(1): 84-99. ISSN: 1993 8012.

Miller, I.; Freund, J. y Johnson, R. 2005: Probabilidades y Estadísticas para ingenieros. Cuarta Edición. México: Prentice-Hall Hispanoamericana S.A.

Moreno, C.; Martínez, J.; Leiva, G.; Roque, A.; Novo, R.; Costa, A.; ... y Limia, M. 2017: Doce preguntas y respuestas sobre energía eólica. La Habana: Editorial Cubasolar. 603 p.

Rivera, S. 2004: Estado del Arte en la Ubicación Óptima de Capacitores y Estudio de Optimalidad de la Solución mediante Búsqueda Exhaustiva. Revista Ingeniería e Investigación, 56: 67-72. Consulta: 14/02/2019. Disponible en: Disponible en: https://www.researchgate.net/publication/259074530 _Estado_del_Arte_en_la_Ubicacion_Optima_de_Capacitores_y_Estudio_de_Optimalidad_de_la_Solucion_mediante_Busqueda_Exhaustiva

Roque, A. 2019: Estimación y pronóstico del recurso eólico en Cuba. En: Taller CUBAEOLICA 2019. Centro de Física de la Atmósfera, Instituto de Meteorología, Cuba, 10-12 julio.

Serrano, J. C. 2013: Comparación de métodos para determinar los parámetros de Weibull para la generación de energía eólica. Scientia et Technica, 18(2): 315-320. Universidad Tecnológica de Pereira. ISSN: 0122-1701. Consulta: 14/02/2019. Disponible en:Disponible en: https://dialnet.unirioja.es/descarga/articulo/4384040.pdf

Terrero-Matos, E.; Legrá-Lobaina, A. A. y Lamorú-Reyes, A. 2014: Método de inverso de la potencia de la distancia para estimar la velocidad del viento. Ingeniería Energética, 35(3): 263-273. ISSN: 1815-5901.

Valdés, J. M. y Vinagre, C. 2012: Modelos de previsiones del viento. Departamento de Ingeniería Eléctrica, Escuela de Ingeniería, Pontificia Universidad Católica de Chile, Santiago. Consulta: 14/02/2019. Disponible en: Disponible en: http://hrudnick.sitios.ing.uc.cl/alumno12/viento/index.html .

Recibido: 11 de Marzo de 2019; Aprobado: 03 de Septiembre de 2019

^*Autor para la correspondencia: [e-mail]

Los autores declaran que no existen conflictos de intereses.

ETM: idea original, obtención e interpretación de datos, redacción del manuscrito y revisión de la versión final.

AALL: análisis de datos, revisión y aprobación de la versión final.