INTRODUCTION
Several constitutive models for the simulation of the mechanical response of the soil using the finite elements method have been developed, since the material behavior of the soil is quite difficult to describe, due to the great variety of existing soils and to their non-linear response when subjected to stress, in both the loading and the discharge process (Wulfsohn & Adams, 2002).
Shen and Kushawaha (1998), classified the constitutive models used to describe the stress-strain relation of the soil as linear and non-linear models (taking into account the shape of the stress-strain curve), elastic, plastic and elastoplastic models (depending on the plasticity of the material), static and dynamic models (depending on the inclusion, or not, of time).
Within these, linear models find their greatest application in stress analysis in structural elements, being the nonlinear models the ones of greatest use in studies related to agricultural soil mechanics. Considering the elements that define the elasticity and plasticity of soils, the elastoplastic models are the most used ones in simulating their mechanical response when being interacted by the working organs of farming tools, because, they assume that the soil can undergo plastic, elastic or elastoplastic strain depending on the magnitude of the applied loads (Shen y Kushawaha, 1998).
At international level, several constitutive models that show the soil as a non-linear elastic or elastoplastic material have been developed. The ones that have reached greatest use are the elastoplastic models of Morh-Coulomb (1776), mentioned by Drucker and Prager (1952) in their extended and modified versions. Besides, Cam Clay or Cambridge developed by Roscoe et al. (1958) and later modified by Roscoe & Burland (1968); the elastic nonlinear model initially developed by Kondner & Zelasko (1963) and modified by Duncan & Chan (1970); the elastoplastic of Lade (1977), and the plastic model of Bailey et al. (1984).
Therefore, the present paper aimed to analyze the current state of the constitutive models used in modeling the mechanical response of agricultural soils in order to define which of them is the most suitable to simulate the mechanical response of agricultural soils with clay texture (Oxisol, Inceptisol and Vertisol). All that with the premise of the predictions accuracy, their advantages and disadvantages as well as their inclusion or not in professional programs for this purpose.
CONSTITUTIVE MODELS
Mohr-Coulomb Model. It is based on the linear failure criterion of Mohr-Coulomb, which is widely used in investigations of both clay and sandy soils, as well as in rock and concrete studies as a result of its simplicity and comfort (Hong-Cai et al., 2012; Herrera et al., 2013; Consoli et al., 2014; Camacho & Ramos, 2016; Molnar, 2016; Chang & Konietzky, 2018; Sekhavatian & Janalizadeh, 2018), however, it has not been widely used for simulation of the soil-tillage interaction (Bhaveshkumar & Prajapati, 2011). This breaking criterion is generally defined in function of the tangential and the normal tensions in a plane, but it can be transformed in such a way that the tension can be represented in three dimensions (Figure 1). Although represented in this form, it presents corners in its hexagonal section which is a deficiency (Abbo et al., 2011; Labuz y Zang, 2012).
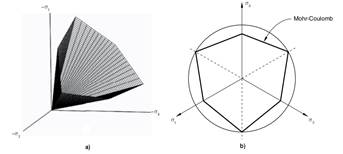
FIGURE 1 Mohr-Coulomb model. a) Mohr-Coulomb failure surface in the main tension space (Nieto et al., 2009);b) Mohr-Coulomb creep surface in the plane of deflection stresses (Hibbit, 2008a).
This model considers that the flow potential of the soil is linear and continuous in the southern plane of the stresses (q-p), ensuring that the flow direction is only defined in this plane. Hence, in this case, the soil flows in an associated way (Figure 2), it also includes that once the soil begins to flow plastically, can be deformed by hardening or softening.
It is implemented in most commercial software available for simulation using the finite element method, requiring six parameters as input data, which can be determined by means of conventional tests (direct shear and triaxial compression), performed in soil mechanics laboratories. It has been widely used in studies related to the determination of the mechanical response of both sandy and clayey soils (Rashidi y Gholami, 2011; Herrera et al., 2013).
According to Bishop (1966), it adjusts better the experimental data than the criterion of Drucker & Prager (1952); however, Herrera et al. (2008), obtained evidence that the Mohr-Coulomb model is not able to predict with the required accuracy the tension state of the soil and its strains, especially when the soil is deformed by softening. They also found that, in this model, both dilatancy and hardening played a secondary role in the predictions. For the humidity conditions (40% humidity) good results were obtained in the predictions where the soil showed a plastic failure, as long as it was considered in the model that the soil could not be deformed by hardening. Taking into account these results, the aforementioned authors do not consider this model is suitable for the simulation of the mechanical response of oxisols.
Drucker-Prager Model. It was developed to represent the plastic deformation of soils (Drucker and Prager, 1952). It is ruled by a creep criterion depending on the applied pressure that determines if the material has exceeded the elastic limit or not. It is a tighter version of the Mohr-Coulomb model, so it can be expressed in function of the cohesion and the internal friction angle. The original model and its variants have recently been applied to studies of soils, rocks, concrete, foams, polymers and other materials (Ucgul et al., 2014; Hamlaoui et al., 2015; Shin et al., 2015; Hammi et al., 2017), finding great application in researches related to the simulation of soil mechanical response, pneumatic-soil interaction, soil compaction, and soil-farming tool interaction (Herrera, 2006; Herrera et al., 2008; Biris et al., 2009; González, 2011; González et al., 2012; Nankali et al., 2012; González et al., 2013a; González et al., 2013b; Nasiri et al., 2013; Armin et al., 2014; Gonzalez et al., 2014; Moslem & Hossein, 2014; Ibrahmi et al., 2015; Chiorescu et al., 2017).
When it is represented in three dimensions, a conical surface is used (Figure 3), which makes it more suitable from the mathematical point of view, since it solves the problem of the corners of the hexagonal section that appear in the pyramid of the Mohr-Coulomb model (Shen & Kushawaha, 1998).
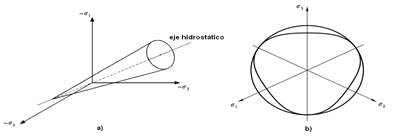
FIGURE 3 Drucker-Prager model a) Drucker Prager Extended creep surface in the space of the main tensions with conical section (Mouazen & Neményi, 1999b). b) Drucker Prager Extended creep surface on the plane of the diverting stresses (Hibbit, 2008a).
The model includes the possibility of considering the soil as a dilatant material that flows in the normal direction to the creep surface, taking the dilatation angle the same value as the creep surface angle Ψ=β. This same criterion was successfully used by Mouazen & Neményi (1999b), Mouazen & Neményi (1999a) and Mouazen et al. (1999) during the simulation of the cutting of a sandy loamy soil by a farming tool. Although researchers like Grujicic et al. (2009), reported that when the flow criterion is applied in this model, excessive dilatation is obtained, which affects the accuracy of the predictions, and constitutes a limiting factor of the model.
The model also gives the possibility to consider the soil as a non-dilatant material from the implementation of a non-associated flow rule, where the soil does not flow in the normal direction to the creep surface, where Ψ<β. It was used by Herrera (2006); Herrera et al. (2008) and González (2011), with this configuration, in the simulation of the mechanical response (soil- farming tool interaction and soil compaction) of an Oxisol, obtaining that the most accurate predictions took place when considering the non-associated flow rule Ψ<β (Herrera, 2006; Herrera et al., 2008), not so in the investigations developed by González (2011).
This model was later used by de la Rosa et al. (2013), with the objective of evaluating its validity in the simulation of the mechanical response of a Vertisol from the central region of Cuba, taking into account the possibilities of the model to predict the changes of tensions as product of the strains by softening or hardening with great accuracy. In addition, it requires a few parameters as input data, which can be obtained in soil mechanics laboratories by means of conventional tests (flat cutting and triaxial compression) and it is included in most professional programs for simulation using the finite elements method.
The results of the investigation showed that the accuracy of the Drucker Prager Extended model in the prediction of the mechanical response of Vertisol, depends on the soil humidity and density status, as well as on the configuration of the model, oscillating the absolute average error from 8.58. % to 27.93%. The greatest accuracy in the prediction of the stress-strain relation was reached when the soil was considered as a dilatant material (Ψ=β) and the coefficient relating the deviating stresses (K) was in function of the humidity content and densification state of soil (K=0.8, K=calculated and K=1). When considering the soil as a non-dilatant material (Ψ=0) and independently of the value it takes (K), numerical impressions that made the convergence of the solutions impossible were presented, once the deviating efforts went over the value of the creep tension. This result allows affirming that this model presents difficulties to predict the mechanical response of the soil once the deviating stress go over the value of the creep tension. Therefore, the parameters that cause the inaccuracies are related to the plastic deformation phase and not to the elastic phase, since in the last one the errors in the prediction are minor.
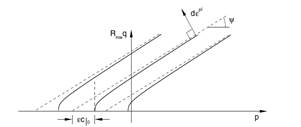
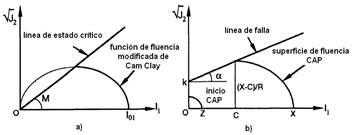
Cam Clay Model. According to Munda et al. (2014), it is one of the most used models to represent the mechanical response of normally consolidated clays. It was developed by Roscoe et al. (1958), for normally or slightly consolidated clays (Figure 4), later modified by Roscoe & Burland (1968), to explain the plastic and volumetric strain of the soil before and after its failure, using a creep surface of the capsule type (Herrera, 2006). This model has had great application in studies related to the mechanical resistance of soils in general (Mendoza et al., 2014). In the case of agricultural soils, it has been mainly used in studies related to soil compaction (Tekeste et al., 2013), although they have also found applications in the simulation of soil-farming tool interaction (Plouffe et al., 1999) and tire-soil interaction (Poodt et al., 2003). Its accuracy to predict changes in soil volume, adapting to both cohesive and sandy soils, as well as accurately predicting the stress-strain relation constitute its main virtues.
However, there are disadvantages like a high demand of computational resources (González et al., 2013a), in addition to requiring between 11 and 14 input parameters, depending on the way the model is implemented, which require specialized equipment for their determination. On the other hand, Mendoza et al. (2014), reported that this model is not capable of representing all the characteristics for clay-textured soils.
Hyperbolic Model of Duncan and Chan. It is a non-linear elastic model that assumes that the stress-strain curves can be approximated to a hyperbola. It was initially proposed by Kondner & Zelasko (1963) and later it was presented incrementally by Duncan & Chan (1970), based on the use of a constant Poisson coefficient, which implied a linear relation between the axial tension and the volumetric strain, representing a limitation of the model. Duncan (1980), later suggested a new equation for the volumetric module, although it still remained a limitation of the model. It has been successfully used in sandy, clayey and silty soils, showing a great capacity to accurately predict the stress-strain relation of the soil when it presents a plastic failure (Chi & Kushawaha, 1988; Chi, 1990; Chi & Kushawaha, 1991; Herrera et al., 2010), as well as in the correlational analysis between the spatial characteristics of the roots and the elastic-plastic properties of the soil (Li et al., 2017). However, its main limitation consists on the inability to predict the changes of tension as product of the strain by softening or hardening. Chi and Kushawaha (1988), refer as a deficiency of this model, the monotonous nature of the function once the tensions increase with the strain increase. Herrera et al. (2010), found this same deficiency observed by Chi and Kushawaha (1988), in three Cuban clay soils (Oxisol, Inceptisol, Vertisol). Another limitation is that it is not implemented in most of the commercial software used for computational simulation using the finite element method.
Despite these limitations, this model was greatly used in the simulation of the soil-farming tool interaction at the end of the last century as referred by Young & Hanna (1977); Bailey et al. (1984); Chi & Kushawaha (1989); Chi (1990); Chi & Kushawaha (1991); Kushawaha & Shen (1995) and Rosa & Wulfsohn (1999), since it meets the requirements for the selection of the constitutive models proposed by Chi (1993), that is, simplicity; possibility of determining the parameters and convenience of implementation.
Elasto-Plastic Model of Lade. It is based on a special creep criterion for low cohesive soils (Lade, 1977). Within this model, two theories of hardening work are used, the first one for the CAP type creep surface (Figure 5), and the other one for a conical creep surface (Lade, 1977; Lade and Boonyachut, 1982). This model is mainly applied to cohesive granular materials (Zhang et al., 1986; Fonseca et al., 1998).
In this theory, the total increase in tension is divided into the following components:
The component of elastic incremental strains, which are calculated by means of Hooke's generalized Law (Timoshenko and Goodier, 1970).
The component of incremental strains caused by plastic deformation. This deformation is not recoverable during discharge. The plastic collapse, according to the theory of plasticity, is governed by the function of the creep surface (Lade, 1977).
The incremental component of plastic expansive strains. They are unrecoverable because of the deviating stress action. The expansive behavior is governed by the creep surface of Lade (1977).
This model was later improved by Lade & Nelson (1984), they developed a procedure to establish an incremental matrix with intersection of multiple creep surfaces, making possible to consider the soil as a dilatant or non-dilatant material, from the implementation of a flow rule associated or not with respect to each creep surface. The possibility of predicting tension changes due to strain, softening or hardening was included. However, the research conducted by Chi et al. (1993), corroborates that the Lade equation does not accurately predict the mechanical response of cohesive soils, especially when the volumetric strains are higher than 10%.
Another disadvantage is that it is not implemented in the main commercially available software for simulation using the finite element method, in addition to needing more parameters as input data than other models (14 in total), which must be obtained with conventional tests in the laboratories of soil mechanics, but needing specialized instrumentation.
Bailey Model. It has been used in studies related to the compaction of agricultural soils, in which its great accuracy in predicting volumetric strain under hydrostatic compression has been shown (Bailey et al., 1984; Chi, 1993). It expresses the soil compaction by means of an exponential model that was modified by Bailey & Johnson (1989), to include the failure or rupture tension. Johnson & Bailey (1990), later proposed a new equation to include in the volumetric strains those strains caused by constant stress.
The disadvantages of this model are that it is not implemented in most of the commercially available software for the simulation by means of the finite element method, although it only needs six input parameters for the implementation of the models. They cannot be determined through conventional tests in soil mechanics laboratories, because they need specialized instrumentation.
CONCLUSIONS
Analyzing the models described above, the ones with greater use in the simulation of the mechanical response of agricultural soils are Drucker Prager Extended Model, Cam Clay Model and Duncan Chan Model. However, Cam Clay Model needs a high demand of computational resources and requires between 11 and 14 input parameters according to the way it is implemented, which determination demands specialized equipment. Duncan Chan Model is not implemented in the majority of commercially available software using the finite element method.
Finally, it is concluded that the Drucker Prager Extended Model is the most suitable one to simulate the mechanical response of an Oxisol, considering in the first place its simplicity, convenience at the time of determining its parameters, its accuracy in estimating the stress-strain relation of soil, and its inclusion in most commercial software.










 texto em
texto em