My SciELO
Services on Demand
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Cuban Journal of Agricultural Science
On-line version ISSN 2079-3480
Cuban J. Agric. Sci. vol.49 no.3 Mayabeque July.-Sept. 2015
ORIGINAL ARTICLE
Historical, mathematical and nutritional bases of Pearson Square as a fit method for ruminant rations
Bases matemático-nutricionales e históricas del Cuadro de Pearson como método de ajuste de raciones para rumiantes
A.A. Santana,I L.A Pernía,I D.A Santana,II
IUniversidad de Granma, Bayamo, Granma, Cuba.
IICentro Universitario Municipal de Campechuela, Granma, Cuba.
ABSTRACT
To analyze the historical evolution and the mathematical and nutritional bases of Pearson square, as fit method for ruminant rations, with the objective of proposing a faster and more professional substitute way, a documental research was performed and theoretical methods of research were also applied. It was possible to conclude that the method is old, simple in its procedure and, because of its mathematical basis, exact and adaptable to the rations formulation for ruminants, adjusting a nutrient and the dry matter required with two feeds, but it can be substituted by a simple equation stated at the end of the research, which allows to save time and steps with more professionalism.
Key words: Pearson square, method, rations, formulations, equations.
RESUMEN
Para analizar la evolución histórica y las bases matemáticas y nutricionales del Cuadro de Pearson, como método de ajuste para raciones destinadas a rumiantes, con el propósito de proponer una vía sustitutiva más rápida y profesional, se efectuó una investigación documental y se aplicaron además, métodos teóricos de investigación. Fue factible concluir que el método es antiguo, sencillo en su proceder y, por su basamento matemático, exacto y adaptable a la formulación de raciones para rumiantes, ajustando un nutriente y la materia seca requeridos con dos alimentos; pero que puede sustituirse por una ecuación simple que se propone al final del trabajo la cual permite ahorrar tiempo y pasos con más profesionalidad.
Palabras clave: Cuadro de Pearson, método, raciones, formulación, ecuaciones.
INTRODUCTION
The current situation of the tropical livestock forces professionals and technicians to optimize the use of all their resources. Today, it has been decreed that the implementation of reasoning and mathematical means in the biological sciences must transform them in next decades (NRC2005). In this process, the ration formulation for animals is very important, because the feeds represent the highest cost of the animal production.
The understanding and control of the calculation methods is very important for this end, since the knowledge level of those who formulate the rations may influence on the use efficiency of this material resource. The researches that have been carried out on nutritious valuation of feeds have made possible that, at present, ruminant rations adjusted on the basis of many nutrients and, mainly, from different divisions. As a consequence, there has been an evolution from the classic adjustments of dry mater intake (DMI), crude protein (CP), total of digestible nutrients (TDN), metabolizable energy (ME), until the most current adjustments of net energy (NE), metabolizable protein (MP), digestible protein in the intestine (DPI), essential amino acids (EAA) and neutral detergent fiber (NDF) (García and Cáceres 1984, Lanzas et al 2008 and van Amburgh et al. 2009).
In spite of it, regardless of which and how many nutrients are wanted to adjust, the calculation procedures will be the same, except that while more control you has of them, more easier, faster and with more precision and conveniently the rations formulas will be fitted.
Considering the above, the objective of this study was to analyzed the historical evolution of the mathematical and nutritional bases that allow to use necessarily and appropriately the Pearson Square (PS), as fit method of ruminants rations, so that allows to propose a substitute way more faster and professional.
MATERIALS AND METHODS
A methodological combination, consistent with the logical necessity of the subject matter was anticipated. A documentary research was firstly carried out, in which the current principles were considered (Denzin and Lincoln 2005 and Corbin and Strauss 2008) and the inquiry categories centered in Pearson Square and its homologous Cruz de Cobenze were checked, as search descriptors, in internet and in printed documents from scientific institution libraries (Universidad de Granma, Universidad de Oriente, Instituto de Ciencia Animal, Estación Experimental de Pastos y Forrajes “Indio Hatuey”, Instituto de Investigaciones “Jorge Dimitrov”), production entities (Complejo Agroindustrial “Enidio Díaz Machado”, located at Campechuela municipality, Granma province), and in others that belong to several specialists of the field.
The search of publications with more edition time was prioritized, because it is of interest to study the chronological evolution of methods. From the triangulation process and references convergence, the information was systematized and categorized, according to opinions that facilitated the sources contrast, allowing chronologically organizes and select documents of more scientific rigor. Join to it, there were also carried out some confirmation interviews to highlight the relevance criteria of the Pearson or Cruz de Cobenze method, so as to confirm that they were always important in the sectors and they are use for many years.
The documents editorials were also valued, as criteria to approach the documental sources authenticity.
As it was necessary, the research theoretical methods were also used (analytic- synthetic, inductive- deductive, historical- logical) to carry out the documental research phases, and to guarantee the propositions and recommendation novelty, according to Hernández-Sampier (2003).
RESULTS AND DISCUSSION
The Simple Pearson Square is one of the most used methods to formulate rations. This is because it is simple, it can mechanically learn by the less educated, without knowing their mathematic bases, and allows to adjust with two foods (or food mixtures) exactly the amount of dry matter and of a nutrient that requires an animal that, as is refers in the literature, and for what the practice has shown, it is preferred the energy or the protein, in expression form. Authors as Afolayan and Afolayan (2008) and Omidiora et al. (2013) showed this way, to mention some.
It is recognized in all consulted publications that if it is needed to adjust a ration so that it contains 10.5% of CP (need N) with a food “A”, that has 7.8%( concentration in A, CA) and one “B” of 16.0%(CB), then must take into account the requirements and carried out the steps and following calculation:
1. To verify that all units in which the composition and need (%) are expressed be equals.
2. To guarantee that one of the two foods contain a value higher to the need and lower in the other one. This is decisive to choose the two foods with those the nutrient will be adjusted or to notice if the available foods (or mixtures) can be used to adjust the need by means of this method.
3. To draw a square or rectangle, in which are written down in the left angles the values of the relative contributions (CA and CB) of the two foods and in the center, the wanted concentration (N). It can also make a cross.
4. To calculate the absolute differences (d1 and d2) of both contributions with the need
d1-|CB-N|; d2=|CA-N|
5. To add the two differences (d1 + d2).

From these two absolute differences (5.5 and 2.7) and the sum (8.2), the inferences that are bellow can be made. Also notice that CA-CB= d1 d2
• The ration DM consists on 5.5 (d1) parts of the food “A” and 2.7 (d2) of “B”.
• For each kg of the ration DM, should be use 0.6707 kg of DM of “A” (5.5/8.2) and 0.3293 kg of MS of “B” (2.7/8.2), which is the rest.
• The remaining DM of the ration will have 67.07 % of “A”
( [d1/d1+d2]x100 = [5.5x100/8.2] ) and 32.93 % of “B” ( [d2/d1+d2]x100 = [2.7x100/8.2] ).
With the calculations carried out in any of the three previous ways, it must obtain a combination of A and B, so CP is 10.5%.
For these reasons, Person square is simple, and assures that there is precision in a nutrient and in the dry matter of the ration. However, they are always imposed several logical questioning, when the method is described to beginners, students and to the onlookers or autodidacts: to explain that the difference between the food contribution and the need are written down in the square opposed diagonal, and it generate the proportion that should be used of the other food.
It is suppose that if a ration for cows of 500 kg weight is adjusted, in milk production (11 kg/d with 3.5 % of fat), and star grass (Cynodon nlemfuensis), of regular quality, with the possibility of also given, as average 1.506 kg of commercial concentrate per animal, as well as sugar molasses and leucaena foliage (Leucaena leucocephala).Of previous measures, it was obtained that the star grass availability was of 24.25 kg per animal.
It is necessary to explain that as PS allows to obtain two quantities of food that cannot vary, and if you has four foods, of which two are fixed (24.25 kg of star grass and 1.516 kg of concentrate),then with the other two is that is intended to adjust the ME or the CP. This explains one of the method limitations and, in turn, the need of always combine it with others, so, to exactly satisfy the need of the adjusted nutrient, the two proportions or obtained percentages are invariable, unique, and could happen that the achieved values are not convenient for physiological and economical reasons, as it can be the higher concentrate relation: forage. It is suggested, therefore, to calculate the nutrients contributions of the two first foods, to compare them with the nutritious requirements and to adjust the difference with the use of molasses and leucaena.
After knowing the nutritional benefits of the amounts of star grass and concentrated preparation, an adjustment to the difference in a nutrient (ME or CP) and DM was performed, with the two feeds available for it (molasses and leucaena), which is possible with PS. The difference obtained shows that there are still missing 51.18 MJ of ME and 399 g of CP to provide to the animal, at a maximum of 5.245 kg of DM, which is the remaining of the DMI. Then, these three values need to be adjusted.
As a preference of who formulates the diet, choosing between ME and CP could be subtracted to apply Pearson. But the needs (51.18 MJ and 399 g) are expressed in units, different to the contributions of ME (MJ/kg) and PB (%) of feed (table 1 and 2). And this is where emerges a big difference in the application of the method on rations for ruminants, regarding its use to formulate industrial mixtures, which is resolved by transforming the needs of units from quantity to density in the remaining DM (5.245 kg). Therefore, one of the demands to apply the square is fulfilled.
This calculation should be performed to know if the two feeds chosen to complete the difference (molasses and leucaena) meet the condition that one possesses higher density than necessity, and the other is lower (table 1), for the nutrient to be adjusted using the square or, what is the same, available feed that could be selected in case of having several of them. In addition, it is also useful for expressing the EM and PB of the square, and the needs in the same units, as required by the method.
Molasses and leucaena meet this requirement for both nutrients. Therefore, PS can be used to adjust the remaining ME or CP to complete the ration.
For feeding ruminants, the most logical aspect is to adjust ME because this is the nutrient that regulates the DMI (NRC 1987, Minson 1990 and Illius and Jessop 1996).
The ME of ration should be adjusted as follows:
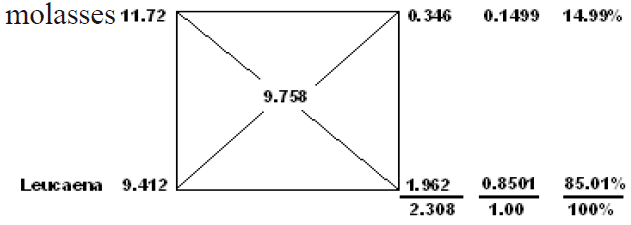
With this proportions, the remaining ME (9.758 MJ/kg or 51.18 MJ) should be adjusted, as it appears when the amounts DM of each feed are calculated, according to the previous proportions and later, the contributions of this nutrient. From the total amount of DM (5.245 kg), 0.786 kg came from molasses and 4.459 kg from leucaena.
Finally, the ME of the ration is adjusted with the two selected feeds for it, and the total ration is composed by 24.25 kg of star grass, 1.516 kg of concentrated, 14.86 kg of leucaena foliage and 1.064 kg sugar cane molasses (table 4).
During the historical evolution of ration formulation, it is known that, up to 1987, the original reference to PS has not been found, which name, according to Benson Institute (2005), comes from the author. However, important authors are cited, who referred its use since 1961 (Trujillo-Figueroa 1987), but, in 1948, the square method was used to mix dairy products up to the desired percentage of fat (Morrison 1948). Kellem and Church (1998), Jurgen and Bregendhal (2007) and Chiba (2014) also recognize the use of this method for this purpose. This way it was confirmed that, dates after 1961, the “last name” of Pearson could be added to this method.
There are reports about the existence of a former method, which is identical to the PS, called Cobenze Diagram, used for producing sugar since the end of 1800´s. To this end, it is used in the sugar cane factory because of the need to obtain a molasses, with certain purity, from two molasses of different purity, according to the findings of Spencer and Meade (1917), which is the eighth edition of the original text, edited for the first time in 1889 (it was also cited later in Spencer 1918, Meade 1963 and Clark and García-López 1963), and it is currently used (Domínguez 2001 and García et al. 2014).
Regarding the mathematical bases of the two methods, Trujillo-Figueroa (1987) stated that there were no answers regarding the procedures of the method, and needed to make his own approach, which could be or not in correspondence with those considered by Pearson. Before the questioning of why the differences are noted in the opposite corner or why they are added, this author proposes an explanation through the construction, in a coordinate axis, of a triangle that encloses the solution.
It is also true that if they are included in a numerical axis, as fragments, the values involved in the initial statement of PS, considering, as an example, the need of fitting (N) 9.758 MJ/kg DM with leucaena (A), with a concentration of 9.412 MJ/kg DM (CA) plus molasses (B) of 11.72 MJ/kg DM (CB), the origin of the method could be deduced (figure 1):
This representation also shows the need of a feed to contain a concentration of the nutrient under the level of necessity, and another over it. The value of N may range between CA and CB, without affecting the solution of the problem. However, if the need to fit is inferior to CA or superior to CB, there will be no possible solution.
Taking into account the calculations of A and B proportions, expressed in percentage, the following can be stated:
1. A= d1/d1+d2)x100 and B=(d2/d1+d2)x100
Demonstration:
From the nature of the problem, two equations can be stated:
2. [(CA/100)xA]+ [(CB/100)xB]=N (I)
3. A + B = 100 (II)
After multiplicating (I) by 100, the result is:
4. CA A + CB B = 100 N
5. A + B = 100
After multiplicating (I) by, the result is:
6.[(-CA/CB)xA-B=(-100/CB)xN
A + B = 100
If both equations are summed:
A-[(CA/CB)xA]+B-B-100-(100/CB) x N (III), are removed
Multiplying (III) by CB , the result is:
8. CBA-CAA=CB100-100N
The common factor in both sides is determined:
9. A (CB-CA) = 100 (CB -N)
10. A-[(CB-N)/(CB-CA)]x100
Knowing that CB-N=d1 and that CB-CA=d1+d2, then:
11. A=(d1/d1+d2)x100
This way, it was demonstrated that the original mathematic source of the ideas of Pearson square, or of the cited Cobenze Diagram, and that the square simply emerge as didactic resources to solve problems of this type in a mechanical way, without many mathematical abstractions.
Considering all the previous explanations on the functioning and mathematical basement of PS, as a mathematical method for adjusting rations for ruminants, the interpretation of the meaning of the two equations is interpreted and the information on the square is used, which, as an example, has been stated previously to adjust ME. Then, the following equation may be stated:
11.72 M + 9.412 L = 9.758 1
M + L = 1 2
Then:
L = 1 – M
1 is substituted in,
11.72 M + 9.412 (1 - M) = 9.758 (R)
11.72 M + 9.412 – 9.412 M = 9.758
2.308 M = 9.758 – 9.412
2.308 M = 0.356
M = (0.356/2.308) = 0.1499, so L= 0.8501
It is confirmed that the same proportions of Pearson are obtained. However, the most important practical recommendation is to establish directly this equation (R), because it allows to avoid all the Pearson procedure. In addition, it is more professional for those with superior levels of instruction.
This equation, which puts the calculation of the two in function of a single variable, can be stated directly, since it is known that the amount of the second feed is always the sum of both minus the first one. Then it can also be stated as 11.72 (1 - L) + 9.412 L = 9.412 L, which allows to calculate the amount of L instead of M.
It is faster if an equation (R)* is stated, which is works with the need expressed in quantity, because it is possible to obtain directly the amount of DM of both feeds to fit the desired nutrient, which is faster and advantageous for reaching the same final results reported in table 4 y 5.
Table 3 shows the need to adjust, in 5.245 kg DM, the 51.18 MJ remaining to complete with molasses (M) and leucaena (L).
11.72 M + 9.412 (5.245 - M) = 51.18 (R)*
11.72 M + 49.37 – 9.412 M = 51.18
2.308 M = 51.18 – 49.366
2.308 M = 1.814
M = (1.814/2.308) = 0.786 kg MS; then, L= 5.245 – 0.786 = 4.459 kg MS
A similar result to that of table 3 is obtained when stating “11.72 (5.245 - L) + 9.412 L= 51.18.
It can be concluded that PS is a method for formulating rations, which could have come from a similar method used in the sugar and/or dairy industry, exact to its mathematical basement, which can be adapted to ruminant rations expressed in quantity, but it can be replaced due to the highest speed and professionalism, simple equation (as those cited (R)* and (R)*) and obtain the same results.
In any of the previous cases, there is an inflexibility of the procedures of the methods, which limits them, and may give unacceptable amounts of feeds, from zoo-technical, economical and nutritional points of view.
This paper may help to increase the culture of professional ethics, precision, and creativity among those in charge of formulating rations for animals.
REFERENCES
Afolayan, M. O. & Afolayan, M. 2008. ‘‘Nigeria oriented poultry feed formulation software requirements’’. Journal of applied Science Research, 4 (11): 1596.
Chiba, L. I. 2014. ‘‘Diet Formulation & Feed Ingredients’’. In: Animal Nutrition Handbook, 2nd ed., Boca Raton, USA: CRC Press, pp. 575–633.
Clark, J. A. & García, L. F. 1963. ‘‘Empleo de la Cruz de Cobenze en los cálculos sobre mezclas de distintas purezas’’. In: El proceso de fabricación de azúcar crudo en los tachos, La Habana, Cuba: Ciencia y Técnica, Instituto Cubano del Libro, pp. 263–296.
Corbin, J. & Strauss, A. 2008. Basics of qualitative research. 3rd ed., CA, USA: Thousand Oaks, 25-48 p.
Denzin, N. K. & Lincoln, Y. S. 2005. The Sage handbook of qualitative research. 3rd ed., CA, USA: Thousand Oaks, 1-32 p.
Domínguez, F. J. 2001. Modelación, Simulación y Optimización del Proceso de Transferencia de Masa que ocurre en la cristalización de azúcar por enfriamiento a nivel industrial. Ph.D. Thesis, Universidad de Matanzas ‘Camilo Cienfuegos’, Matanzas, Cuba, 45-82 p.
García, T. R. & Cáceres, O. 1984. Nuevos sistemas para expresar el valor nutritivo de los alimentos y el requerimiento y racionamiento de los rumiantes. Matanzas, Cuba: EEPF ‘Indio Hatuey’, 44 p.
García, Y., López, Y. & Benítez, A. 2014. ‘‘Optimización del sistema energético de un central azucarero para maximizar el excedente de bagazo’’. Rev Avanzada Científica, 17 (1): 00–00.
Hernández, S. R. 2003. Metodología de la investigación. vol. 1–2, La Habana, Cuba: Félix Varela.
Illius, A. W. & Jessop, N. S. 1996. ‘‘Metabolic constraints on voluntary intake in ruminants’’. J Anim Sci., 74: 3052.
Instituto Benson. 2005. Formulación de raciones. , Available: <http://benson.byu.edu/Publication/Lessons/Spanish/Lessons/ Animal/Raciones.htm>, [Consulted: December 12, 2005].
Jurgens, M. H. & Bregendahl, K. 2007. Animal feeding and nutrition. 10th ed., Dubuque, IA, USA: Kendall/Hunt Publishing Co., 62-82 p.
Kellems, R. O. & Church, D. C. 1998. Livestock feeds and feeding. 4th ed., Upper Saddle River, NJ, USA: Prentice_Hall, Inc., 35-49 p.
Lanzas, C., Broderick, G. A. & Fox, D. G. 2008. ‘‘Improved feed protein fractionation schemes for formulating rations with the Cornell net carbohydrate and protein system’’. J Dairy Sci., 91: 4881.
Meade, G. P. 1963. Spencer-Meade Manual de fabricación de azúcar de caña y químicos especializados. Barcelona, España: Montaner y Simón S.A., 769-771 p., Traducido por Mario García Menocal.
Minson, J. D. 1990. Forage in ruminant nutrition. San Diego, CA, USA: Academic Press, 34-47 p.
Morrison, F. B. 1948. Feeds and Feeding: A handbook for the student and stockman. 21st ed., NY, USA: The Morrison Publishing Company, 238-239 p.
NRC. 1987. Predicting feed intake of food-producing animals. Subcommittee on Feed Intake, Committee on Animal Nutrition, National Research Council, USA, Available: <www.nap.edu/catalog/950.html>, [Consulted: December 12, 2012].
NRC. 2005. Mathematics and 21st Century Biology. Committee on Mathematical Sciences Research for DOE’s Computational Biology, USA, Available: <http://www.nap.edu/catalog/11315.html>, [Consulted: December 12, 2012].
Omidiora, E. O., Adegoke, B. O. & Aderounmu, G. A. 2013. ‘‘Review of livestock formulation techniques’’. Journal of Biology, Agriculture and Helathcare, 3 (4): 69.
Spencer, G. L. 1918. Manual de fabricación de azúcar de caña y químicos azucareros. 7th ed., New York: John Willey & Sons, Inc., 445-446 p.
Spencer, G. L. & Meade, G. P. 1917. Cane sugar handbook. A manual for cane sugar manufacturers and their chemists. 8th ed., New York: John Willey & Sons, Inc., 638-640 p.
Trujillo, F. V. 1987. Métodos matemáticos en la nutrición animal. McGraw-Hill, 240 p.
van Amburgh, M. E., Overton, T. R., Chase, L. E., Ross, D. A. & Recktenwald, E. B. 2009. ‘‘The Cornell Net Carbohydrate and Protein System: current and future approaches for balancing of amino acids’’. In: 71st Meeting, Proceedings of the Cornell Nutrition Conference for Feed Manufacturers, East Syracuse, New York, USA, pp. 28–37.
Received: January 13, 2015
Accepted: July 16, 2015
A.A. Santana, Universidad de Granma, Bayamo, Granma, Cuba. Email: santana@udg.co.cu














