My SciELO
Services on Demand
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Cuban Journal of Agricultural Science
On-line version ISSN 2079-3480
Cuban J. Agric. Sci. vol.50 no.1 Mayabeque Jan.-Mar. 2016
Cuban Journal of Agricultural Science, 50(1): 11-23, 2016, ISSN: 2079-3480
ORIGINAL ARTICLE
The bootstrap: a 35 years old young very useful for analyzing biological data
El bootstrap: un joven de 35 años muy útil para analizar datos biológicos
J. A. Navarro Alberto,I
IDepartamento de Ecología Tropical Campus de Ciencias Biológicas y Agropecuarias Universidad Autónoma de Yucatán Km 15.5 Carretera Mérida-Xmatkuil. CP 97315. Mérida, Yucatán, México.
ABSTRACT
In diverse scientific discussion forums and in specialized journals the word “bootstrap” has been mentioned or read. Will it be that for analyzing our data we must use boots with straps for its use as support points for jumping? (How odd…but this is the word for word translation!). In this paper the significance and development of the bootstrap is reviewed as rigorous statistical calculation method for data analysis. The diverse algorithms associated with the estimation by bootstrap intervals are shown and its application with the problem relative to mean estimation is explained. Finally mention is made of the implications and limitations of this method, as well as of the great usefulness it has in biological and agricultural sciences which have adopted it as analysis tool since its invention by Bradley Efron (U. of Stanford) since more than 35 years ago.
Key words: Bootstrap, interval of confidence, biological data, median.
RESUMEN
En diversos foros de discusión de científicos, en revistas especializadas hemos oído mencionar o leído la palabra “bootstrap”. ¿Será que para analizar nuestros datos debemos usar botas con cintillos y usar éstos como puntos de apoyo para saltar? (¡Que cosa más rara... pero esta es la traducción literal de la palabra!). En este trabajo revisaremos el significado y desarrollo del bootstrap como método estadístico de cómputo intensivo para el análisis de datos. Se mostrarán los diversos algoritmos asociados con la estimación por intervalos bootstrap y se ilustrará su aplicación con el problema relativo a la estimación de la mediana. Finalmente, se hará mención de los alcances y limitaciones de este método, así como la gran utilidad que tiene dentro de las ciencias biológicas y agropecuarias, que las han adoptado como herramienta de análisis desde su invención por Bradley Efron (U. de Stanford) hace más de 35 años.
Palabras clave: Bootstrap, intervalos de confianza, datos biológicos, mediana.
INTRODUCTION
In statistics it is customary to discuss about means and errors (standard) of variables in continuous scale: weights of seven months old steers, daily milk yield in dairy cows, etc. The strategy for the analysis of these variables for statistical inference is assuming that there is only statistical variation and that having a sufficient number of measurements is enough so as to calculate the mean and the standard error of the mean, knowing that the standard error decreases as the number of measurements increases. The artillery of statistical methods in these cases is vast and it is commanded by one of the most important theorems of Statistics: the Theorem of Central Limit: “If random size samples are taken n, y1, y2…yn of a population with finite mean µ and variance σ2, then for an n sufficiently large, the sampling mean distribution (sampling means) can be approximated with a function of normal density with mean µȳ=µ and standard deviation (standard error) σȳ=σ/√n. The error that will be committed due to the approximation of the distribution of the sampling means to the normal will decrease as n increases. For example, in figure 1, the sampling distributions generated on selecting the samples of normal random variables or uniform are approximately normal even for n as small as 10 (figures A1, B1). On the other hand, for biased distributions such as square ji the mean sampling distribution is not normal for n = 10 (figure C1), and only for n values as large as 100 is that this distribution is practically normal (figure C2).
In many cases, our variables of interest have unknown distribution and thus, it is not possible to know how large the sample must be in order to apply the result of the Theorem of Central Limit. If we rely on the results (asymptotic) of the Theorem of Central Limit these could not satisfy the level of accuracy with a relatively small sample. If the suppositions on the population are incorrect, then the sampling distribution can be quite inaccurate. In addition, it can be very difficult to deduce mathematically the sampling distribution of the statistical of interest. All these questions can be latent since with only one sample of particular size it seems to be impossible establishing which the sampling distribution is. The idea of the bootstrap focus on this situation: only one data set is available by hand of a certain size and questions if it is possible determining the sampling distribution of its data without using the Theorem of Central Limit. Bootstrapping is a general approach of statistical inference based on these ideas of creating the sampling distribution for a statistics through re-sampling of data close at hand.
The formalization of the bootstrap method is owed to Bradley Efron (Efron 1979 and Efron and Tibshirani 1993) who took ideas from various precursor statistical procedures: the random sampling of finite populations, the estimation of variances from various samplings, stratified semi-samplings and inference methods of intensive calculation, specially Monte Carlo and the jackknife. Efron describes in the above mentioned paper the difficult decision for choosing the name of the method, motivated by the audacity of Tukey (1958) for naming in a special way his methods (jackknife, stem and leaf diagram, box and mustache graphic). Tukey proposed the jackknife by analogy with those big pocket razors that have a great many different tools that are “pulled” so as the user will be capable of solving many small tasks without using some better tool. Statistically speaking, the jackknife is a general approach to prove hypotheses and calculate confidence intervals. It was originally introduced by Quenouille (1949, 1956) as a method of bias reduction, when there were no best methods to be used. This can happen when it is difficult the estimation of statistics, due to the fact that the sampling distributions cannot be exactly deduced or its bias is not known and thus, it is difficult to create confidence intervals. In the case of the bootstrap, the term invented by Efron he refers to someone that “pulls” himself upwards with the bands of its boots. With this strange expression, Efron wanted to reflect the use of the only sample available for giving rise to many others. In this paper the bootstrap will be reviewed as a statistical method of intensive calculation for data analysis. Diverse algorithms with be shown associated with the estimation by bootstrap intervals and its application will be presented with the problem relative to mean estimation. Finally, mention will be median of the scopes and limitations of this method.
MATERIALS AND METHODS
Procedure of the Bootstrap. It is assumed that a sample is taken M = {y1, y2,…,yn} of a population P= {y1+y2...yn}, that N is much larger than n, and that M is a simple random sample or an independent random sample of the P population. It is assumed that the elements of the population are scaled (although it can be considered as multivariate data) and that interests some statistics T = t (M) as an estimation of the corresponding population parameter (Ɵ = t(P). The decision of choosing the bootstrap method (specifically, the non-parametric bootstrap) is due to the fact that the exact T distribution cannot be deduced and neither is it possible using the alternative of asymptotic results because there is no accurate fulfillment in those cases in which there is only a relatively small sample.
For performing the non-parametric bootstrap, no suppositions are made on the population form, but a random sample is selected of the n size of the M sample (as the sample were from an estimation of the population, P), with replacement sampling (for avoiding that only the original M sample stays). The M sample play the role of P population, from which repeated samples are taken, the bootstrap samples. If it is called the first bootstrap sample M*j={y11,y21….y*n1}, then each selected element from M, y*il from M, will be part of the bootstrap sample, with l/n probability, that is, copying the selection of the M sample of the P population. Repeating this procedure many times for selecting many bootstrap samples, for example N times, it will be obtained, in general, the j-th bootstrap sample M*j={y1j,y2j….y*n1}. For finding the bootstrap estimation of the T statistics, the following steps are taken:
1. For each M*j bootstrap sample, calculate the statistical values T*j,j=1….n (If the T*j distribution is created around the original T estimation, then this distribution is similar to the sampling T distribution surrounding Ɵ).
2. Estimate the expected value of the T sampling distribution through the estimation of the expected value of the bootstrap estimations, using the mean of the calculated statistics in the bootstrap samples,
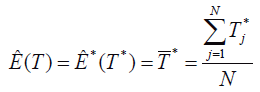
There is no guarantee that the Ȇ(T) estimator would be unbiased, so part of the bootstrap procedure is estimating the bias for Ȇ(T)=T*. On the other hand, the T, B=T-Ɵ bias can be estimated as B*=T*-T
3. If you wish to have an estimation of the standard error of the sampling T distribution, calculate the estimation of the standard error of the bootstrap estimations using the standard deviation of the statistics calculated in the bootstrap samples,

Similarly as it happens with Ȇ(T) there is no guarantee that the estimator of the standard error of T, calculated through the bootstrap samples is accurate. This step could be omitted as in the cases of the estimation of confidence intervals of bootstrap by the percentile methods described below.
If instead of selecting randomly bootstrap samples for obtaining the Ê*(T*) and ÊE*(T*)estimators, all possible bootstrap samples of n size are numbered for generating all the elements of the B(n)={Mj*Mj*set, it is a bootstrap sample of n size so that E*(T*) and EE*(T*) can be accurately calculated, this from the computational point of view would be prohibited. The number of possible bootstrap samples (B (n) cardinalship) is very large unless in case n is small. It can be demonstrated that such number is:
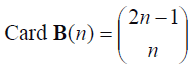
For example, Card B(15) = 7.8 x 107; Card B (20) = 6.9 x 1010.
In the bootstrap inference, combined to the mistake committed using a particular M sample for representing the population, a second mistake is made by not listing completely all bootstrap samples. This latter mistake can be controlled making a sufficiently large number of bootstrap repetitions.
At first the bootstrap method can be seen as an analogy in which the estimation method is based at times. If F is the distribution of the population that generated a random sample of size n, then the estimator T and its sampling distribution G (T) can be considered as F functions. Efron suggested that it is possible to substitute F by a consistent estimation Ȇ This estimated distribution Ȇ is a function of empirical distribution assigning the sample probability, l/n, to each observation in the random sample. Finally what Efron made was to estimate the sampling distribution G(T) with the bootstrap distribution of the statistical values G*(Ȇ) by Monte Carlo simulation.
Estimation by bootstrap confidence intervals. From its origin, one of the main research tasks in bootstrapping has been the development of methods for calculating valid confidence limits for population parameters (figure 2). These methods are of very diverse kinds and are mainly differentiated by the assumptions made on the estimators and simulation algorithms for obtaining bootstrap samples. Manly (2007) describes some of these methods. The most popular are:
-Standard bootstrap (normal method): It suppose that the bootstrap estimator has an approximately normal distribution and the bootstrap re-sampling gives a good approximation of the statistical standard error of interest.
-First percentile method (percentile method of Efron (l979). The limits of 100 (1 – α)% are determined with values of the bootstrap distribution of the statistics of interest occupied by the percentiles 100 (α/2)% and 100 (1 – α/2)%. In this procedure it is supposed that there is a monotonous transformation of estimator values distributed normally.
-Second percentile method (Hall’s method). It is based on generating the distribution of the difference between the bootstrap estimation and the estimation of the parameter calculated with the original sample.
-Percentile with corrected bias. It corrects any bias arising from applying the first percentile method, making the median of the estimator distribution be equal to the mean. The algorithm of the percentile method with corrected bias uses a more complex algorithm than the first percentile since in the confidence limits takes into account the proportion of times that the bootstrap estimation is higher than the estimation of the parameter using an original sample.
-Percentile with correction by accelerated bias. Proposed by Efron and Tibshirani (1986), it assumes that there is also a monotonous value transformation of the estimator normally distributed, but the mean and standard error of this distribution are linear functions of the transformation itself as could happen when the standard error of the distribution varies with the mean.
-Bootstrap-t. It uses a t pivotal statistic calculated for each bootstrap sample. The calculations in this algorithm are more intensive, requiring calculating the parameter estimators, as of its standard error, for each bootstrap sample (this standard error could be calculated by jacknife)
Bootstrap confidence limits for the mean. In some statistical texts (e.g. Sokal and Rohlf 2012) is presented the formula: EEsampling median= 1.253 σ/ √n,
where α is the population standard deviation of a continuous random variable, Y. If α is not known, then its substitution with the sampling standard deviation would only be valid for large samples and normal distributions. But it could occur that the distribution of variables of the random variable Y does not follow a normal one, making invalid the application of the estimator of the median standard error, and thus, the calculation of the confidence limits for this parameter. In the case of Y variables, positively biased, that follow a distribution log normal, an alternative method can be used involving taking Y, = log (Y) as variable approximately normal for calculating the conventional confidence interval based on the t of Student for Y, mean. The median parametric confidence interval will be obtained by applying the transformation backwards the interval for this mean. Given the restrictions for applying these parametric methods of median estimation, the use of non-parametric methods is generally chosen. The most common are:
1. Quantiles of binomial distribution with percentile p = 0.5. These quantiles are the same used for the median sign test (Hollander and Wolfe 2011). Given a confidence level (1 – α) x 100%, the binomial probabilities supply inferior (x’) and superior (x) critical values, corresponding to half the significance level, α/2. These critical values correspond to RInf=x’+1 and Rinf= n-x’=x ranges of the arranged sample so as the values of the variable occupying those places, yRinf and yRinfwill constitute the confidence limits of (l – α) x 100 % for the mean. This method is adequate for small samples, that is, n ≤ 20 (Helsel & Hirsch 2002).
2. Approximation of the method of binomial quantiles to the normal distribution. It is preferably applied for large samples (n > 20) and it is based on critical values of the standard normal zα/2. The confidence limits for the median yRinf and yRinf will be those values of the arranged sample occupying places offered by the following expressions, conveniently rounded off to the closer whole numbers:
Rinf=(n-zα/2√n)/2 y Rinf=(n+zα/2√n)/2+1
3. Method based on the range test with Wilcoxon sign. It is based on the equivalence of the statistics T+ of this test with the average number of Walsh positive. Walsh averages for a sample {y1, y2…,yn} constitute a set of n (n + 1)/2, numbers Wij=(yi+yj)/2,i<j. When Walsh averages are arranged from lesser to greater, W(1),W(2),……,W(n(n+1)/2) , the confidence limits can be calculated following the same procedure of the quantile method of the binomial distribution. The mean of the Walsh averages can be used as estimator (from Hodges-Lehmann) of the distribution median from where the sample was taken under the supposition that such distribution was symmetric. If the distribution is not symmetric, then the estimator will be denominated the pseudo-median.
4. Non-parametric bootstrap. This method is described with the following example: Figure 3 shows the values of DDT concentration, measured in 12 specimens of the American perch, sampled in the Tennessee River (Sincich 1993). In view of the positive bias observed in the sample of DDT concentrations, it is reasonable to use the median as summary measurement of the value distribution center of the variable Y = “DDT concentration” and presenting a confidence interval for the median for inference purposes.
In total, nine methods were applied. First, the backwards transformation of the confidence interval was utilized for the median of log (Y), under the supposition that Y is distributed log-normally. For avoiding the possibility of assuming any distribution, for the variable Y it was also estimated the confidence interval for the median based on non-parametric methods. Methods 1-3 were applied which were described in the previous section and also the bootstrap (4) was employed, according to the procedure illustrated in figure 2 for inferring the sampling distribution of the sampling median based on the examined sample. For this, the bootstrap distribution (empirical) of the median estimations was generated by simulation, in which each median was estimated from the random selection with substitution of the DDT values for obtaining later the median non-parametric bootstrap confidence limits. The estimation methods used were five: Standard or Normal, First Percentile Method, Second Percentile Method (also called “Ordinary”), Percentile of Correction by Accelerated Bias and Bootstrap-t. The calculations were made with functions of the R program (R Core Team 2015) and the “simpleboot” package (Peng 2008).
RESULTS AND DISCUSSION
Results from the estimations by intervals for the median concentration of DDT with the use of the nine methods described in the section “Confidence limits for the median”, are set out in table 1. It can be noticed that the normal bootstrap method, the second percentile method and the bootstrap-t produce confidence intervals whose lower limits are negative. However, the parametric space of the median is no-negative since the DDT concentration values are also no-negative. Therefore, such lower limits must be changed to 0. Under this criterion, the smallest confidence interval is generated by the second percentile method. A graphic summary of the estimated confidence limits with this method is shown in figure 4.
Which is the best method (parametric or non-parametric) for estimating confidence intervals for the median? From the set of data analyzed it can be discerned that the functioning of the different estimation methods by intervals for the median is very variable. Surprisingly, the parametric interval exceeds in its accuracy the non-parametric methods. In addition, the percentile methods and the percentile with correction by accelerated bias estimate bootstrap intervals for the median similar to those calculated with conventional non-parametric methods. It also attracts attention the bootstrap intervals producing negative limits, in spite that the parametric space is the set of real no-negative numbers. This brings about the need of modifying the result for obtaining sensible results. What has been observed with this small example of median estimation is recurrent in statistics: there is no clear “winner” as best estimator of some parameter especially when the sample is relatively small. This also applies, in particular, to the non-parametric bootstrap methods. As Manly (2007) indicates it is not possible anticipating in general which of the bootstrap methods allows obtaining better estimations of a parameter. The bright side regarding the use of the bootstrap is that it increases the options for obtaining sensible estimations by parameter intervals of interest in practically any area of applied sciences.
Bootstrap has been used for estimating standard errors and creating confidence intervals of parameters of only one sample, but the procedure can be extended for the estimation of parameters of two o more samples and for bootstrap hypothesis tests. For example, for median comparison of two samples a test statistics (based on the medians of each sample and the overall median) can be selected so as its value is comparable to a bootstrap distribution for which the null hypothesis is true. An alternative approach implies adjusting the sampling values through the residues (the difference between each datum and the sample median to which it belongs). A description of these two approaches of bootstrap tests for two samples can be seen in Manly (2007). In this same reference there is an extensive list of bootstrap application methods in biological sciences, especially in Ecology, Genetics, Evolution, Community Ecology and Environmental Studies.
In the field of agricultural sciences bootstrap is less used but not for that is less important. A recent example is the work of Cubayano et al. (2015) who assessed the accuracy of prediction models of reproductive values in beef cattle. These authors used bootstrap for comparing the prediction reliabilities of reproductive values of some complex traits. Another recent paper is that of Narinç et al. (2015) comparing two median estimations of three parameters characterizing the color of egg yolks: one was the conventional median estimation and the other the bootstrap estimation. This type of study, in which the conventional parametric methods and the bootstrap are applied and compared, is frequent in animal science. Hence, in the determination of reference intervals of physiological parameters in animals, the bootstrap confidence intervals seem to have better performance under conditions where the conventional parametric methods are not applicable. Examples of these studies of reference intervals are those carried out by Bennett et al. (2006) with physiological parameters in greyhounds and by Cooper et al. (2014) with biochemical and hematological parameters in pigs. In other estimation problems, as the determination of the sample size in studies searching for the optimization of the number of samples, the bootstrap method has shown to be a good alternative (see Bravo-Iglesias 2010 and Bravo-Iglesias et al. 2013).
The strategy of realizing statistical bootstrap tests for solving problems that have to do with the analysis of variance of one or various factors, the multiple regressions or the survival has been used in numerous agricultural and animal sciences investigations. In the majority of the cases, the bootstrap is utilized for proving the fit goodness of models or its selection (Casellas et al. 2006, Sahinler and Karakok 2008 and Tarrés et al. 2011, Faridi et al. 2014 and Rodríguez et al. 2013). Additionally, it has been employed for the control of error rates Type I in multiple tests (Meuwissen and Goddard 2004 on false discovery rates in the comparison of two treatments affecting the expressions of a considerable amount of genes).
Since the publication of the classical papers of Efron (1979), the use of bootstrap has been explosive since many persons have found in the method complete response to difficult questions. The most popular bootstrap method is the one having the simplest theoretical bases: Efron’s percentile. The users are more reluctant to use the other methods due to the sophistication of the supporting theory. For example, Manly and Navarro (2009) applied bootstrap-t for estimating the confidence interval for the difference of two medians when the variances are very different and distributions are very biased and these authors found very imprecise results. Therefore, the bootstrap must be utilized careful in situations in which it has not been thoroughly tested. Theory guarantees that the bootstrap will function well in certain situations with large samples, but with small samples it is not possible anticipating if it will operate better or worst (¡) than the parametric and conventional non-parametric methods. Prior suggesting the particular utilization of bootstrap for small samples, it is recommended testing the procedure with simulated samples. Undoubtedly the bootstrapping applications for confidence intervals and significance tests will continue developing in the future and only those methods with clear properties and with computer support for its operation in standard statistical packages will prevail.
REFERENCES
Bennett S., Abraham L., Anderson G., Holloway S. & Parry B. 2006. ‘‘Reference limits for urinary fractional excretion of electrolytes in adult non-racing Greyhound dogs’’. Australian Veterinary Journal, 84 (11), pp. 393–397, ISSN: 1751-0813, DOI: 10.1111/j.1751-0813.2006.00057.x.
Bravo I. J. A. 2010. Aplicación del método Bootstrap para la estimación de parámetros poblacionales en Parcelas Permanentes de Muestreo y en la modelación Matemática en plantaciones de Pinus cubensis Griseb. Ph.D. Thesis, Universidad Pinar del Río, Cuba.
Bravo J., Torres V., Rodríguez L., Montalvo J., Toirac W., Fuentes V. & Rodríguez P. 2011. ‘‘Determinación del tamaño de muestra en parcelas permanentes de muestreo mediante la aplicación del método bootstrap’’. Revista Forestal Baracoa, 32 (1), pp. 57–65, ISSN: 0138-6441.
Casellas J. 2006. ‘‘Parametric bootstrap for testing model fitting in the proportional hazards framework: An application to the survival analysis of Bruna dels Pirineus beef calves’’. Journal of Animal Science, 84 (10), pp. 2609–2616, ISSN: 0021-8812, 1525-3163, DOI: 10.2527/jas.2005-729.
Cooper C. A., Moraes L. E., Murray J. D. & Owens S. D. 2014. ‘‘Hematologic and biochemical reference intervals for specific pathogen free 6-week-old Hampshire-Yorkshire crossbred pigs’’. Journal of Animal Science and Biotechnology, 5, p. 5, ISSN: 2049-1891, DOI: 10.1186/2049-1891-5-5.
Cuyabano B. C. D., Su G., Rosa G. J. M., Lund M. S. & Gianola D. 2015. ‘‘Bootstrap study of genome-enabled prediction reliabilities using haplotype blocks across Nordic Red cattle breeds’’. Journal of Dairy Science, 98 (10), pp. 7351–7363, ISSN: 0022-0302, DOI: 10.3168/jds.2015-9360.
Efron B. 1979. ‘‘Bootstrap Methods: Another Look at the Jackknife’’. The Annals of Statistics, 7 (1), pp. 1–26, ISSN: 0090-5364, 2168-8966, DOI: 10.1214/aos/1176344552, MR: MR515681Zbl: 0406.62024.
Efron B. & Tibshirani R. J. 1994. An Introduction to the Bootstrap. CRC Press, 456 p., ISBN: 978-0-412-04231-7.
Faridi A., Golian A., Mousavi A. H. & France J. 2013. ‘‘Bootstrapped neural network models for analyzing the responses of broiler chicks to dietary protein and branched chain amino acids’’. Canadian Journal of Animal Science, 94 (1), pp. 79–85, ISSN: 0008-3984, DOI: 10.4141/cjas2013-078.
Manly B. F. J. 2006. Randomization, Bootstrap and Monte Carlo Methods in Biology. 3rd ed., Boca Raton, FL: Chapman and Hall/CRC, 480 p., ISBN: 978-1-58488-541-2.
Manly B. F. J. & Navarro J. 2009. ‘‘Bootstrap Tests and Confidence Intervals for Non-Normal Data’’. In: Ronja F. (ed.), Neue Methoden der Biometrie: Beiträge des 55. Biometrischen Kolloquiums an der Leibniz-Universität Hannover 2009, Hannover, Germany: Institut für Biostatistik, p. 76.
Meuwissen T. H. E. & Goddard M. E. 2004. ‘‘Bootstrapping of gene-expression data improves and controls the false discovery rate of differentially expressed genes’’. Genetics, selection, evolution: GSE, 36 (2), pp. 191–205, ISSN: 0999-193X, DOI: 10.1051/gse:2003058, PMID: 15040898PMCID: PMC2697185.
Narinç D., Aygün A., Küçükönder H., Aksoy T. & GÜRCAN E. K. 2015. ‘‘An Application of Bootstrap Technique in Animal Science: Egg Yolk Color Sample’’. Kafkas Üniversitesi Veteriner Fakültesi Dergisi, 21 (5), pp. 631–637, ISSN: 1300-6045, 1309-2251.
Peng R. D. 2008. Simpleboot: Simple Bootstrap Routines. R package. version 1.1-3, Available: <https://cran.itam.mx/bin/windows/contrib/3.2/simpleboot_1.1-3.zip> .
Quenouille M. H. 1949. ‘‘Approximate tests of correlation in time-series 3’’. Mathematical Proceedings of the Cambridge Philosophical Society, 45 (03), pp. 483–484, ISSN: 1469-8064, DOI: 10.1017/S0305004100025123.
Quenouille M. H. 1956. ‘‘Notes on Bias in Estimation’’. Biometrika, 43 (3/4), pp. 353–360, ISSN: 0006-3444, DOI: 10.2307/2332914.
Quinn G. P. & Keough M. J. 2002. Experimental Design and Data Analysis for Biologists. Cambridge, New York: Cambridge University Press, 560 p., ISBN: 978-0-521-00976-8.
R Core Team. 2015. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing, Available: <https://www.R-project.org/> .
Rodríguez L., Larduet R., Martínez R. O., Torres V., Herrera M., Medina Y. & Noda A. C. 2013. ‘‘Modelación de la dinámica de acumulación de biomasa en Pennisetum purpureum vc. king grass en el occidente de Cuba’’. Revista Cubana de Ciencia Agrícola, 47 (2), pp. 119–124, ISSN: 2079-3480.
Sahinler S. & Karakok S. G. 2008. ‘‘Bootstrap and Jackknife Parameter Estimation of the Models Fitting to Lactation Milk Yield (2x305) on Calving Age’’. Journal of Applied Animal Research, 34 (1), pp. 39–44, ISSN: 0971-2119, DOI: 10.1080/09712119.2008.9706937.
Sincich T. 1993. Statistics by Example. 5th ed., New York: Dellen Pub Co, 1024 p., ISBN: 978-0-02-410981-1.
Tarrés J., Fina M., Varona L. & Piedrafita J. 2011. ‘‘Carcass conformation and fat cover scores in beef cattle: A comparison of threshold linear models vs grouped data models’’. Genetics Selection Evolution, 43 (1), pp. 1–10, ISSN: 1297-9686, DOI: 10.1186/1297-9686-43-16.
Tukey J. W. 1958. ‘‘Bias and confidence in not quite large samples’’. The Annals of Mathematical Statistics, 29 (2), pp. 614–623, ISSN: 0003-4851, DOI: 10.1214/aoms/1177706647.
Received: November 25, 2015
Accepted: March 11, 2016
J. A. Navarro Alberto, Departamento de Ecología Tropical Campus de Ciencias Biológicas y Agropecuarias Universidad Autónoma de Yucatán Km 15.5 Carretera Mérida-Xmatkuil. CP 97315. Mérida, Yucatán, México. Email: jorge.navarro@correo.uady.mx














