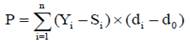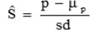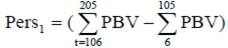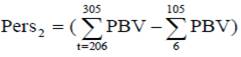My SciELO
Services on Demand
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Cuban Journal of Agricultural Science
On-line version ISSN 2079-3480
Cuban J. Agric. Sci. vol.52 no.2 Mayabeque Apr.-June 2018 Epub June 01, 2018
Biomatemática
Estudio de la persistencia del rendimiento de la leche utilizando las metodologías de predicción y regresión aleatoria en vacas lecheras Holstein iraníes
1Department of Animal Science, Mashhad Branch, Islamic Azad University, Mashhad, Iran
Los datos consintieron de 435 390 registros del rendimiento del día de pesaje de leche en vacas primíparas de 659 rebaños con partos de 2001 a 2011. La evaluación de la persistencia a través de la metodología de mejor predicción demostró que la correlación fenotípica de esta medida de persistencia y el rendimiento lechero total fue 0.450, mientras que el mejor día de referencia, la heredabilidad de la persistencia y el rendimiento lechero estimados a los 305 d por este método fueron el día 130, 0.11 y 0.305, respectivamente. Las heredabilidades de la persistencia del rendimiento lechero para Pers1 (valor genético predicho de 106 a 205 días en la leche, restado del valor genético predicho de 6 a105 días en la leche) y Pers2 (valor genético predicho de 206 a 305 días en la leche, restado del valor genético predicho de 6 a105 días en la leche), calculados por la metodología de regresión aleatoria, fueron de 0.09 a 0.185, respectivamente. Los resultados demostraron que el método de mejor predicción es potente y exacto para medir persistencia. Sin embargo, debido a la flexibilidad de la metodología de regresión aleatoria, algunas medidas de persistencia utilizadas en este método pueden tener alta heredabilidad y correlación genética comparado con el método de mejor predicción. Por lo tanto, se puede concluir que es preferible calcular la persistencia con la metodología de regresión aleatoria que con el método de mejor predicción.
Palabras-clave: efectos genéticos aditivos; curva de lactancia; persistencia; rendimiento total de la leche
La producción de leche y la persistencia son dos características económicas importantes en vacas lecheras. La persistencia se puede definir como la habilidad de la vaca de continuar produciendo leche a un alto nivel después de haber alcanzado el pico de lactancia (Jamrozik et al. 1997) o la habilidad de la vaca de mantener un rendimiento lechero relativamente constante durante la lactancia (Strabel et al. 2001). De este modo, los animales persistentes son aquellos que muestran las curvas de lactancia más estables (Togashi and Lin, 2004). Una alta persistencia o curva estable de lactancia tiene muchas ventajas. Esto permite mejor utilización de fibra barata (Solkner and Fuchs, 1987), reducción del estrés durante la producción pico y aumenta la ganancia (Weller et al. 2006) y, por último, una reducción en los costos reproductivos (Muir et al. 2004). Por lo tanto, animales persistentes generan más tasa de retorno. Grossman et al. (1999) dividieron las medidas de persistencia en tres grupos: 1. Medidas expresadas como proporción (o rango) de los rendimientos; 2. Medidas derivadas de la variación de los rendimientos en el día del pesaje; y 3. Medidas basadas en parámetros estimados de modelos matemáticos de curvas de lactancia. Sin embargo, ninguna de estas mediciones fue el método estándar para calcular persistencia. Las curvas de lactancia con bajos picos pueden ser más persistentes y el rendimiento lechero total puede, como consecuencia, ser mayor en lactancias más persistentes. En la cría de animales se ha utilizado extensivamente la metodología de regresión aleatoria (RRM) para la evaluación genética del ganado lechero (Schaeffer y Dekkers, 1994) y ovino (Kominakis et al. 2001) con los registros del dia de prueba. La metodología de regresión aleatoria del día de pesaje también posibilita la evaluación genética de la persistencia (Jensen 2001 y Mrode et al. 2002). En otras palabras, los valores genéticos para los rasgos de persistencia son derivados de la aplicación de modelos de regresión aleatoria en evaluaciones genéticas de rutina (Harder et al. 2006). Druet et al. (2005) y Togashi y Lin (2006) describieron la persistencia sobre la base de valores propios de las matrices genéticas aditivas de modelos de regresión aleatoria. La evaluación de diferentes medidas de persistencia con el uso del modelo del día de pesaje de Jamrozik et al. (1997) y Jakobsen et al. (2002) demostró que la correlación con rendimientos lecheros de lactancia osciló desde 0.10 a 0.55 mientras que Cobuci et al. (2004) reportaron que la correlación genética entre la persistencia y el rendimiento lechero a los 305 d variaron de 0.86 a 0.99, respectivamente. Cobuci et al. (2007) evaluaron seis medidas diferentes basadas en valores genéticos predichos (VGPs) para describir la persistencia con la metodología de regresión aleatoria solo con el uso de la función Wilmink para modelar la parte fija de la curva de lactancia, genético aditivo (ad) y los efectos ambientales permanentes (e) de los días de lactancia y demostraron que la diferencia de VGP290 - VGP90 y 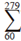 PBV-PBV280 son las más adecuadas para describir la persistencia del rendimiento lechero. Togashi y Lin, (2004) confirmaron que la selección de la proporción de VGP280 a VGP65 (r280/65) mejoró el rendimiento lechero de lactancia y la persistencia. En ese estudio se utilizó una función polinómica Legendre de quinto orden para ajustar la curva de lactancia en el marco de la RRM. La persistencia no se debe relacionar con el rendimiento lechero total y esto permite una selección más eficiente de la persistencia y el rendimiento lechero total simultáneamente (Togashi y Lin, 2004 y Appuhamy et al. 2007). Cole y VanRaden (2006) propusieron un método para calcular la persistencia que es fenotípicamente independiente del rendimiento lechero. En este método la persistencia se puede calcular como una función de la curva de lactancia estándar y una regresión lineal de la desviación del día de pesaje de la vaca, en los días de lactancia. Estos autores proponen que esta definición de persistencia puede ser más útil que los utilizados en modelos del día de prueba. Este estudio tiene el objetivo de evaluar y comparar la persistencia del rendimiento lechero mediante el uso de metodología día de pesaje de regresión aleatoria y la de mejor predicción con vacas primíparas Holstein iraníes.
PBV-PBV280 son las más adecuadas para describir la persistencia del rendimiento lechero. Togashi y Lin, (2004) confirmaron que la selección de la proporción de VGP280 a VGP65 (r280/65) mejoró el rendimiento lechero de lactancia y la persistencia. En ese estudio se utilizó una función polinómica Legendre de quinto orden para ajustar la curva de lactancia en el marco de la RRM. La persistencia no se debe relacionar con el rendimiento lechero total y esto permite una selección más eficiente de la persistencia y el rendimiento lechero total simultáneamente (Togashi y Lin, 2004 y Appuhamy et al. 2007). Cole y VanRaden (2006) propusieron un método para calcular la persistencia que es fenotípicamente independiente del rendimiento lechero. En este método la persistencia se puede calcular como una función de la curva de lactancia estándar y una regresión lineal de la desviación del día de pesaje de la vaca, en los días de lactancia. Estos autores proponen que esta definición de persistencia puede ser más útil que los utilizados en modelos del día de prueba. Este estudio tiene el objetivo de evaluar y comparar la persistencia del rendimiento lechero mediante el uso de metodología día de pesaje de regresión aleatoria y la de mejor predicción con vacas primíparas Holstein iraníes.
Materiales y Métodos
Los datos originales contenían 637 902 registros del rendimiento durante el día de pesaje de leche de 76 713 vacas lecheras primíparas Holstein iraníes con partos de 2001 a 2011. La función gamma incompleta de Wood se utilizó para ajustar las curvas de lactancia, descritas como Yt=atbexp(-ct) . El modelo de Wood y sus parámetros derivados han demostrado que son fuertes para ajustar los datos del día de pesaje en las regiones tropicales y sub-tropicales (Rekik et al. 2003). En esta descripción yt es el rendimiento diario del día t y a está aproximado a los rendimientos lecheros iniciales después del parto, b es el parámetro de pendiente en inclinación hasta el rendimiento máximo, y c es el parámetro de declinación de pendiente (Wood 1969). El rendimiento lechero máximo, los días del rendimiento lechero máximo, y la leche total de 305 d se calcularon como b/c, a(b/c)b exp-b, y 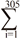 yi respectivamente (Appuhamy et al. 2007). Las curvas atípicas de lactancia, que tuvieron valores negativos de a, b o c no se utilizaron para predecir el rendimiento lechero diario. Los parámetros de cada curva individual se estimaron con el uso de procedimientos no lineales (PROC NLIN) de SAS (Ver. 9.1 SAS Institute, 2004 Cary, NC) a través del método iterativo Gauss-Newton. Por otra parte, la producción parcial desde los días 5-100 (Parte1), 101-200 (Parte2), 201-305 (Parte3) y la producción total desde el día 5-305 (milk305 d) se calcularon individualmente para cada vaca. VanRaden (1998) introdujo un método (mejor predicción) para calcular persistencia que es independiente del rendimiento. De acuerdo con este método, la persistencia es una función de la desviación del rendimiento del día de pesaje de la curva de lactancia estándar (Yi-Si) y la desviación de los días de lactancia del día de pesaje cercana a una fecha de referencia (di d0)
yi respectivamente (Appuhamy et al. 2007). Las curvas atípicas de lactancia, que tuvieron valores negativos de a, b o c no se utilizaron para predecir el rendimiento lechero diario. Los parámetros de cada curva individual se estimaron con el uso de procedimientos no lineales (PROC NLIN) de SAS (Ver. 9.1 SAS Institute, 2004 Cary, NC) a través del método iterativo Gauss-Newton. Por otra parte, la producción parcial desde los días 5-100 (Parte1), 101-200 (Parte2), 201-305 (Parte3) y la producción total desde el día 5-305 (milk305 d) se calcularon individualmente para cada vaca. VanRaden (1998) introdujo un método (mejor predicción) para calcular persistencia que es independiente del rendimiento. De acuerdo con este método, la persistencia es una función de la desviación del rendimiento del día de pesaje de la curva de lactancia estándar (Yi-Si) y la desviación de los días de lactancia del día de pesaje cercana a una fecha de referencia (di d0)
Donde,
P |
- persistencia de la lactancia |
Yi |
-rendimiento del i-ésimo día de pesaje |
Si |
- rendimiento estándar en el i-ésimo día de pesaje |
di |
- días de lactancia en el i-ésimo día de pesaje d0= días de lactancia en la fecha referenciada |
Yi-Si |
- desviación del rendimiento del i-ésimo día de pesaje del rendimiento estándar |
di-d0 |
- desviación de los días de lactancia del i-ésimo día de pesaje de la fecha referenciada |
n |
- número total de días de prueba del rendimiento lechero para calcular la persistencia |
Cole and VanRaden (2006) reportaron que una medida de persistencia que no está fenotípicamente correlacionada con el rendimiento de la lactancia se puede obtener definiendo d0 como el punto de equilibrio entre los rendimientos a inicios y final de la lactancia. Determinaron que d0 fuera 128 días de lactancia para el rendimiento lechero. Un estimado estandarizado de persistencia, Ŝ, se obtuvo entonces con la sustracción de la media de lactancia (μp) y dividiéndola entre la desviación estándar fenotípica de lactancia (sd) de la persistencia calculada:
Actualmente, los cálculos de persistencia se basan derivados del modelo de regresión aleatoria del día de pesaje (Jensen 2001 y Cobuci et al. 2007). La siguiente ecuación muestra el modelo utilizado para el análisis de regresión aleatoria:
donde,
Yjlm |
- observación del día de pesaje n de la vaca 1 obtenida en rebaño-año-estación i |
HYSi |
-efectos fijos de rebaño-año-estación de producción (8 597 clases) |
bj |
- coeficiente de regresión de edad al parto como covariable (en términos lineales y cuadráticos) |
ßm |
- el coeficiente de regresión fija para una curva de promedio de población (funciones Legendre polinomial o Ali y Schaeffer) |
Φm(tm1) |
- m-ésimo edad de lactancia del primer animal en días de lactancia (t= 5, … , 305) |
q |
- orden de la polinómica Legendre ortogonal |
aln |
- coeficiente de regresión aleatoria genético de aditivo para animal I |
pln |
- coeficiente de regresión aleatoria medioambiental permanente para animal I |
eijlmk |
- error residual aleatorio |
Las differente medidas de persistencia basadas en VGP se utilizaron en la literatura (Jakobsen et al. 2002; Cobuci et al. 2007 y Pereira et al. 2012). En este estudio se utilizaron dos medidas diferentes de persistencia (Pers1, Pers2):
Selección basada en la VGP parcial durante la lactancia (VGP de los días de lactancia 106-205 sustraído del VGP de los días de lactancia 6-105):
Selección basada en la VGP parcial durante la lactancia (VGP de los días de lactancia 206-305 sustraído del VGP de los días de lactancia 6-105):
Además, se calculó la predicción de un valor genético a los 305 días de todos los animales, que se obtuvo de la suma de los VGP para todos los días de lactancia, así como por los siguientes criterios: VGP5-100 (Parte1), VGP101-200 (Parte2) and VGP201-305 (Parte3). De acuerdo con las diferentes medidas de persistencia, los bajos valores de Pers1 o Pers2, indican una mayor persistencia porque están asociados a bajas tasas de disminución de la producción. El software PEST (2002) se utilizó para organizar los datos originales. El software VCE6 (Kovac and Groeneveld, 2008) se aplicó para la estimación de los componentes de covarianza, coeficientes de regresión aleatoria de los efectos genéticos aditivos y medioambientales permanentes de cada animal basados en la probabilidad máxima restringida (REML). Los demás parámetros para las matrices de covarianza de los coeficientes de regresión aleatoria (fenotípico, genético aditivo y varianza medioambiental permanente, correlaciones y heredabilidad) se calcularon con el procedimiento IML del software SAS 9.1. Finalmente, los cálculos de las diferentes medidas de persistencia para cada animal se realizaron y evaluaron con el uso de programación SAS.
Resultados y Discusión
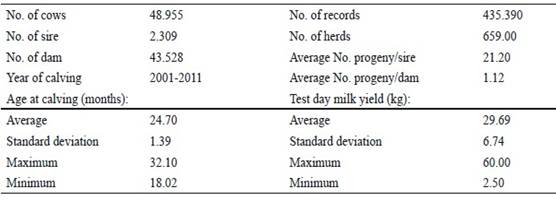
El número de días de prueba por vaca varió de 3 to 10. Todas las vacas se ordeñaron tres veces al día y se conocían a ambos progenitores. La edad de parto estuvo entre 18 y 32 meses, y el rendimiento lechero diario individual estuvo entre 2.5 y 60 kg. Después de editar, quedaron 435 390 registros de días de prueba de rendimiento lechero de 48 955 vacas lecheras. La estructura de los datos y el pedigrí después de editar se resumió en la tabla 1.
Los coeficientes de correlación de Pearson entre la persistencia (Ŝ) y el rendimiento lechero a los 305 d en los días de referencia desde 120 a 130 días se indican en la tabla 2. Esta tabla demuestra que es evidente que el día óptimo de referencia para utilizar en la fórmula de persistencia es 130 días porque la correlación entre el rendimiento lechero a los 305 d y la persistencia fue la más cercana a cero. VanRaden, (1998) propone al día 128 de lactancia como día de referencia en primíparas Holstein, mientras que Appuhamy et al. (2007) reportaron los 128 y 125 días de lactancia como primera y última lactancias en vacas Holstein Americano, respectivamente.
Table 2 Pearson correlation coefficients (r) between persistency and 305 d milk yield at different reference day (d0) in primiparous Iranian Holstein dairy cows

La tabla 3 presenta las heredabilidades por diferentes rendimientos lecheros parciales, parámetros de la curva de lactancia (tiempo máximo, rendimiento máximo y rendimiento lechero total a los 305 d) y Ŝ, que se obtuvo de modelos univariados de animales, así como correlaciones fenotípicas entre estas medidas.
Las tasas de heredabilidad para las diferentes partes de lactancia estuvieron entre 0.23 y 0.30. Esto indica que la mayor heredabilidad se obtuvo en medio de la lactancia y los valores más bajos se encontraron al inicio y al final de la lactancia, que concuerda con los resultados de Jakobsen et al. (2002). La heredabilidad estimada del rendimiento lechero a los 305 d en la primera lactancia fue 0.30. La heredabilidad del rendimiento lechero a los 305 d fue mayor que la informada por Santos et al. (2013) en vacas Guzerat. Estos autores demostraron una heredabilidad de 0.24, mientras que Yamazaki et al. (2014) y Farhangfar y Rowlinson (2007) encontraron heredabilidades de 0.42 y 0.29 en vacas Holstein japonesas e iraníes, respectivamente. En este estudio se estimó una heredabilidad de 0.08 para el tiempo máximo del rendimiento lechero, que fue similar a los reportados por Ferris et al. (1985) de 0.07 en ganado Holstein Americano de primera lactancia y por Muir (2004) de 0.09 en Holstein canadienses de primera lactancia. Los estimados de heredabilidad para el rendimiento máximo y persistencia fueron 0.30 and 0.11, respectivamente (tabla 3). Los estimados de heredabilidad de este estudio para el tiempo máximo, rendimiento máximo y rendimiento lechero a los 305 d son comparables con aquellos reportados por Farhangfar y Rowlinson, (2007) en vacas lecheras Holstein iraníes. Una heredabilidad estimada para la persistencia de la producción de leche de 0.11 indica que esta es un rasgo poco heredable. En general, los estimados de heredabilidad para la persistencia varían significativamente entre las medidas de persistencia. Shanks et al. (1981) informaron heredabilidad por persistencia de 0.02, con la utilización de una función gamma incompleta, pero Batra et al. (1987) encontró heredabilidad de 0.21 para este rasgo en Holstein canadiense, a través de la función gamma. En un estudio de Atashi et al. (2006) de heredabilidades basadas en modelos univariados, estos valores se encontraron entre 0.046 y 0.081, mientras que Pereira et al. (2012) constataron que la heredabilidad varió de 0.10 a 0.25 en ganado Gyr brasileño. En este último estudio las medidas de persistencia se calcularon con la función del valor genético estimado con modelos del día de pesaje de regresión aleatoria.
Table 3 Heritabilities and phenotypic correlations (±SE) between partial milk yields (Part1, Part2 and Part3), peak time (Ptime), peak yield (Pyield) and persistency measures (Ŝ)of primiparous Iranian Holstein dairy cows
Las correlaciones fenotípicas entre rendimientos parciales y el rendimiento lechero a los 305 d osciló entre 0.88 y 0.99 en este estudio. La mayor correlación se obtuvo entre Part2 y el rendimiento lechero a los 305 d. La correlación fenotípica entre el tiempo máximo y el rendimiento máximo es bajo (0.12), lo cual concuerda con lo encontrado por Boujenane y Hilal, (2012). Las correlaciones fenotípicas del rendimiento lechero a los 305 d con el tiempo máximo y el rendimiento máximo fueron 0.354 y 0.890, respectivamente. El rendimiento máximo tiene, por lo tanto, mayor importancia que el rendimiento lechero a los 305 d de lactancia. Esto significa que las vacas de mayor producción pico probablemente tendrán mayor rendimiento lechero a los 305 d y la selección de vacas por su alta producción de leche a los 305 d, basada en su rendimiento máximo, será entonces efectivo. La persistencia de la lactancia se considera una característica muy importante de la curva de lactancia (Farhangfar y Rowlinson, 2007). La correlación de las medidas de persistencia por el método de mejor predicción y Parte1, Parte2 y Parte3 de lactancia mostraron que las vacas con alta persistencia tienden a producir menos leche al inicio de la lactancia y más que al final de la lactancia (tabla 3). Además, la correlación fenotípica entre persistencia y el rendimiento lechero a los 305 d fue 0.45 en este estudio. Según Solkner y Fuchs, (1987), la relación entre rendimiento lechero total y la persistencia depende de las medidas de persistencia. De acuerdo con la definición de persistencia, algunos investigadores calcularon una correlación fenotípica positiva entre la persistencia y el rendimiento lechero a los 305 d, pero algunos otros encontraron que la persistencia se correlacionaba negativamente con el rendimiento lechero total. Farhangfar and Rowlinson, (2007) obtuvieron un estimado de 0.23 por esta relación en novillas Holstein iraníes con el uso de la función gamma incompleta, mientras que Boujenane and Hilal (2012) informaron que la correlación fenotípica entre la persistencia y la producción de leche a los 305 d en vacas lecheras marroquíes a través de la función Wood fue de -0.25.
la mayoría de los valores de Ŝ oscilaron entre -3.8 and +3.8 en esta base de datos. El histograma de frecuencia de la persistencia aparece en la figura 1. La distribución de la persistencia es normal y la persistencia promedio, basada en el método de mejor predicción, se encuentra cercana a cero. La media y la varianza de Ŝ son 0 y 1, respectivamente. El valor positivo de Ŝ indica aumento de la persistencia relacionado con el de la curva de lactancia estándar (el cual se ajustó basándose en la media del rendimiento lechero diario con el uso de la función gamma incompleta) y valores negativos de Ŝ indican disminución de la persistencia (figura 1). Estos resultados son similares a los encontrados por Appuhamy et al. (2007) en la evaluación de persistencia con la utilización del método de mejor predicción en vacas primíparas y multíparas.
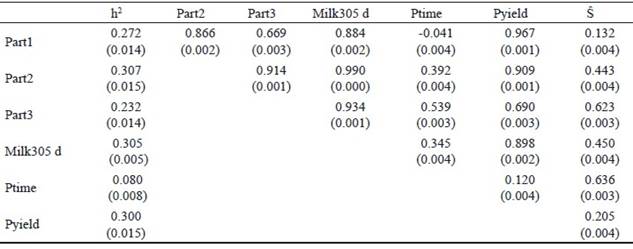
Las curvas de lactancia de vacas con la mayor (Ŝ>3) y menor (Ŝ<3) persistencia, como se define en la metodología de mejor predicción, aparecen en la figura 2. Como se esperaba, la forma de la curva de lactancia en vacas con mayor persistencia es completamente diferente a aquella de las vacas con menor persistencia. Pereira et al. (2012) informaron que la persistencia no depende del nivel de producción lechera ni del valor genético de la leche, pero si está relacionada con la forma de la curva de lactancia para el rendimiento lechero a los 305 d. Además, los cálculos de persistencia con la utilización de la metodología de mejor predicción condujeron a que la persistencia de lactancia fuera independiente del rendimiento lechero a los 305 d, y las vacas con alta persistencia tienen mayores rendimientos en lactancias prolongadas (Cole and VanRaden, 2006). El tiempo máximo de las vacas en este estudio con alta persistencia fue aproximadamente 120 días, pero en las vacas con baja persistencia fue de alrededor de 52 días (figura 2). La correlación fenotípica positiva (0.643) entre el tiempo máximo y la persistencia (tabla 3) sugiere que las vacas que alcanzan el rendimiento máximo atrasadas durante la primera lactancia podrían tener mayor persistencia. Esto concuerda con los resultados de Farhangfar y Rowlinson, (2007), Appuhamy et al. (2007) y Muir et al. (2004), quienes informaron que las lactancias con rendimientos máximos tardíos son más persistentes.
Los estimados de heredabilidad en rendimiento lechero y la proporción de medio ambiente permanente y varianza fenotípica residual como función de la etapa de lactancia se calcularon y se muestran en la figura 3. La heredabilidad del rendimiento lechero aumentó ligeramente a lo largo de la trayectoria de la lactancia, alcanzando el mayor estimado a los 200 a 250 días de lactancia, seguido de ligeras disminuciones hasta el final de la lactancia. La mayor y menor heredabilidad estimada se observa cerca del final (0.24) y a inicios (0.07) de la lactancia, respectivamente. Estos resultados confirman los encontrados por un estudio previo (Elahi Torshizi et al. 2012) y otros de diferentes investigadores (Muir et al. 2007 y Kheirabadi y Alijani 2014), que reportaron la mayor heredabilidad del rendimiento lechero del día de pesaje al final de la lactancia. De acuerdo con estos resultados, la varianza residual fue mayor a inicios de la lactancia y disminuyó gradualmente hasta el final de la lactancia. Sin embargo, la relación del medio ambiente permanente con la varianza fenotípica mostró una tendencia diferente. Takma y Akbas (2007) demostraron que la forma de esta proporción disminuyó al inicio de la lactancia y luego aumentó hasta el final de la lactancia.
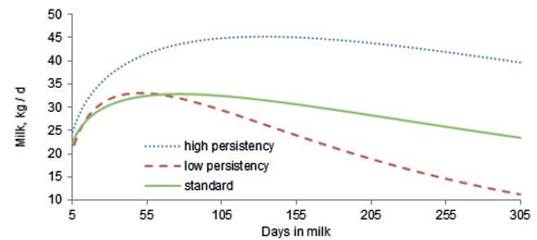
Figure 2 Comparison of lactation curves of cows with high persistency (Ŝ>3), low persistency (Ŝ < -3) and standard lactation curve for Iranian primiparous Holstein cows

Figure 3 Heritability of test day milk yield (solid line), the ratio of permanent environment to phenotypic variance (dashed line) and the ratio of residual to phenotypic variance (dotted line) during lactation by RRM for Iranian primiparous Holstein cows
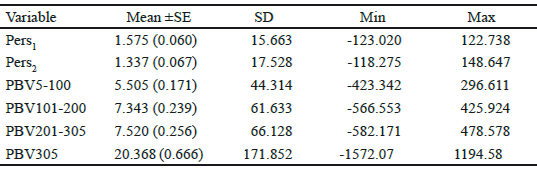
Van Vleck y Henderson (1961) encontraron que los rendimientos al inicio y final de la lactancia estuvieron sujetos a más variaciones del medio ambiente temporal que el rendimiento a mediados de lactancia, lo cual está más influido por diferencias genéticas y del medio ambiente permanente entre las vacas. Los estimados de correlación para efectos genéticos aditivos y del medio ambiente permanente a diferentes días de lactancia a través de la trayectoria de la lactancia, del modelo RRM, se muestran en la figura 4. Como en los resultados de otros investigadores (Jakobsen et al. 2002 y Biassus et al. 2010), con respecto a los resultados del modelo de regresión aleatoria, las correlaciones genéticas y medioambientales entre distintos días de prueba tienden a disminuir en los extremos del período de lactancia, pero cercanos a la unidad en días de prueba adyacentes. La tabla 4 muestra las estadísticas generales para los VGP para las diferentes medidas de persistencia (Pers1 and Pers2), para rendimientos lecheros parciales, así como el rendimiento lechero a los 305 d de vacas lecheras Holstein primíparas iraníes se muestra en la tabla 1. El valor genético promedio de Pers2 es menor que el de Pers1pero Pers2muestra más variación comparado con Pers1. Teniendo en cuenta diferentes medidas de persistencia, los valores bajos de Pers1 and Pers2 indican mejor persistencia porque están asociados con una lenta tasa de disminución en la producción después del valor máximo. Como se muestra en las tablas 4 y 5, parece que Pers2 pudiera describir la persistencia mejor que la medida de Pers1.
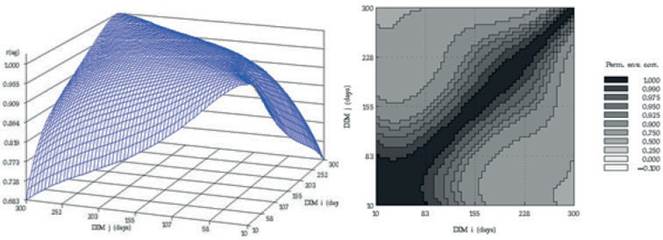
Figure 4 Additive genetic (left) and permanent environmental (right) correlations between days in milk over the trajectory of lactation using a RRM model for Iranian primiparous Holstein cows
Table 4 Mean (±SE), standard deviation (SD), minimum and maximum of PBV for different measures of persistency, partial milk yields and 305 d lactation milk yield of Iranian primiparous Holstein cows
El estimado de heredabilidad de las distintas medidas de persistencia (Pers1 and Pers2), rendimientos lecheros parciales, así como correlaciones genéticas entre los valores genéticos predichos de estas medidas se presentan en la tabla 5. Las heredabilidades para dos medidas de persistencia (Pers1 and Pers2) son 0.090 y 0.185, respectivamente.
Table 5 Heritabilities and genetic correlations (±SE) between the predicted breeding values for different persistency measures and partial milk yields in Iranian primiparous Holstein cows
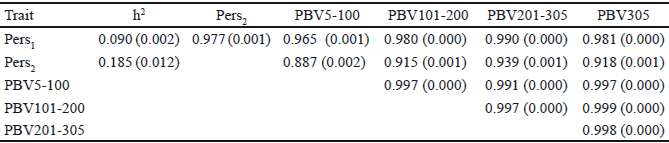
Las heredabilidades de Pers1 and Pers2 con comparables con los resultados de Kheirabadi y Alijani (2014), quienes evaluaron varias medidas de persistencia con la utilización de la metodología RRM multirasgo en vacas Holstein iraníes (0.08 and 0.22), pero fueron diferentes a lo encontrado por Jakobsen et al. (2002), quienes informaron heredabilidades de 0.24 y 0.20 para Pers1 y Pers2, respectivamente, en vacas primíparas danesas Holstein, con el uso de modelos de regresión aleatoria.
Las razones principales para las diferencias en los estimados de heredabilidad pueden atribuirse a las diferencias en el orden de las funciones polinómicas utilizadas en los modelos para la estimación de los efectos genéticos y medioambientales, y también debido a las diferencias en la estructura de las bases de datos. Las correlaciones genéticas entre los VGP de los rendimientos lecheros parciales, persistencia y rendimiento acumulado fueron positivos y altos (tabla 4). Las correlaciones entre Pers1 y Pers2 con los VGP del rendimiento lechero a los 305 d fueron 0.98 y 0.91, respectivamente. Una medida de persistencia con baja correlación con el rendimiento lechero a los 305 d es óptima. Los resultados de este estudio indican que Pers2 tiene mayor heredabilidad y menor correlación genética con el rendimiento lechero a los 305 d comparado con el de Pers1. Por lo tanto, se recomienda la utilización del RRM para medir la persistencia. Esto concuerda con los resultados de Kheirabadi y Alijani (2014), quienes informaron que Pers2 es la medida preferible de la persistencia del rendimiento de la leche en Irán. La heredabilidad de Pers2 es también mayor que la de Ŝ. Biassus et al. (2010) informaron que la heredabilidad de algunas medidas de persistencia (∑t-60EBV-EBV60) and (EBV290-EBV90) que se calcularon con RRM, fue baja. El cálculo de persistencia con los métodos de mejor predicción es simple y potente, este método es independiente del rendimiento con baja correlación con el rendimiento lechero a los 305 d y relativamente poca heredabilidad. Sin embargo, en el RRM se puede utilizar diferente orden de las funciones matemáticas y polinómica Legendre. Por otra parte, se pueden estimar los rendimientos genéticos de cada uno de los días de lactancia con este método y, debido a su flexibilidad, se pueden proponer diferentes medidas de persistencia con mayor heredabilidad y menor correlación fenotípica y genética con el rendimiento lechero total, comparado con el método de mejor predicción. Esto hace que el cálculo de persistencia tenga más ventajas basado en el RRM que los métodos de proporción e incluso mejor predicción de la persistencia de la lactancia.
Conclusiones
La persistencia del rendimiento lechero se evaluó en este estudio con el uso de dos metodologías (regresión aleatoria y mejor predicción). En la metodología de mejor predicción, la correlación fenotípica entre el tiempo máximo y la persistencia fue alta y la curva de lactancia de las vacas con mayor persistencia fue completamente diferente a la curva de lactancia estándar. La heredabilidad y la correlación genética entre varias medidas de persistencia dependen considerablemente de la manera en que se define la medida de persistencia. La alta correlación genética positiva entre las medidas de persistencia del RRM y el rendimiento lechero a los 305 d resultaron en un mejoramiento genético del rendimiento lechero total y, consecuentemente, de la persistencia. La heredabilidad de Pers2 es mayor que la de Pers1 y Ŝ. Por lo tanto, por el uso del modelo de regresión aleatoria, debido a su flexibilidad (funciones y ordenes polinómicas Legendre diferentes ajustadas en partes fijas y aleatorias del modelo y la posibilidad de definir varias medidas de persistencia basadas en los VGPt), podría ser el modelo preferible para la evaluación y selección de vacas por persistencia comparado con el de mejor predicción y otros métodos.
Agradecimientos
Se agradece al Center of Animal Breeding de Iran por proveer los datos utilizados en este estudio.
REFERENCIAS
Atashi, H., Moradi Shahrbabak, M. & Abdolmohammadi, A. 2006. Study of some suggested measures of milk yield persistency and their relationships. Inter. J. Agri . Bio. 3, 378-390. [ Links ]
Appuhamy, J. A., Cassell, B. G., Dechow, C. D. & Cole, J. B. 2007. Phenotypic relationships of common health disorders in dairy cows to lactation persistency estimated from daily milk weights. J. Dairy Sci. 90, 4424-4434. [ Links ]
Batra, T. B., Lin, C.Y., Mcallister, A. J., Lee, A. J., Roy, G. L., Vesseley, J. A., Wautly, J. M. & Winter, A. 1987. Multitrait estimation of genetic parameters of lactation curves Holstein heifers. J. Dairy Sci . 70, 2105-2111. [ Links ]
Biassus, I. O., Cobuci, J. A., Costa, J. A, Rorato, P. N., Neto, J. B. & Cardoso, L. L. 2010. Persistence in milk, fat and protein production of primiparous Holstein cows by random regression models. Revi. Brasil. de Zoote. 39, 2617-2624. [ Links ]
Boujenane, I. & Hilal, B. 2012. Genetic and non-genetic effects for lactation curve traits in Holstein Friesian cows. Arch.Tier. 55, 450-457. [ Links ]
Cobuci, J. A., Euclydes, R. F. & Costa, C. N. 2004. Análises da persistêncianalactação de vacas da raçaholandesa, usandoprodução no dia do controle e modelo de regressãoaleatória. Revi. Brasil. Zoote. 33, 546-555. [ Links ]
Cobuci, J. A., Euclydes, R. F., Costa, C. N., Torres, R. A. & Carmen, S. P. 2007. Genetic evaluation for persistency of lactation in Holstein cows using a random regression model. Gene. Mole. Bio. 30, 349-355. [ Links ]
Cole, J. B. & VanRaden, P. M., 2006. Genetic evaluation and best prediction of lactation persistency. J.Dairy Sci. 89, 2722-2728. [ Links ]
Druet, T., Jaffrezic, F. & Ducrocq, V. 2005. Estimation of genetic parameters for test day records of dairy traits for the first three lactations. Gene. Selec. Evol. 7, 257-271. [ Links ]
Elahi Torshizi, M., Aslamenejad, A., Nassiri, M., Farhangfar, H., Solkner, J., Kovac, M., Meszaros, G. & Malovrh, S. 2012. Evaluation of test day milk yield in Iranian primiparous Holstein using different random regression models. J. Anim. Sci. Adv. (2) 8, 664-667. [ Links ]
Farhangfar, H. & Rowilnson, P. 2007. Genetic analysis of wood's lactation curve for Iranian Holstein heifers. J. Biolo. Sci. 7, 127-135. [ Links ]
Ferris, T. A., Mao, I. L. & Anderson, C. R. 1985. Selecting for lactation curve and milk yield in dairy cattle. J. Dairy Sci . 68, 1438-1448. [ Links ]
Grossman, M., Hartz, S. M. & Koops, W. J. 1999. Persistency of lactation yield: A Novel Approach. J. Dairy Sci . 82, 2192-2197. [ Links ]
Groeneveld, E., Kovac, M. & Wang, T. 2002. PEST user’s guide and reference manual version 4. 2. 3. Department of animal science, University of Illinois. [ Links ]
Harder, B., Bennewitz, J., Hinrichs, D. & Kalm, E. 2006. Genetic parameters for health traits and their relationship to different persistency traits in German Holstein dairy cattle. J. Dairy Sci . 89, 3202-3212. [ Links ]
Jakobsen, J. H., Madsen, P., Jensen, J., Pedersen, J., Christensen, L. G. & Sorensen, D. A. 2002. Genetic parameters for milk production and persistency for Danish Holsteins estimated in random regression models using REML. J. Dairy Sci . 85, 1607-1616. [ Links ]
Jamrozik, J., Schaeffer, L. R. & Dekkers, J. C. M. 1997. Genetic evaluation of dairy cattle using test day yields and random regression model. J. Dairy Sci . 80, 1217-1226. [ Links ]
Jensen, J. 2001. Genetic evaluation of dairy cattle using test day models. J. Dairy. Sci. 84, 2803-2812. [ Links ]
Kheirabadi, A. & Alijani, S. 2014. Genetic parameters for milk production and persistency in Iranian Holstein population by multitrait random regression models. Arch Tier. 57, 12, 1-12. [ Links ]
Kominakis, A., Volanis, M. & Rogdakis, E. 2001. Genetic modeling of test day records in dairy sheep using orthogonal Legendre polynomials. Small. Rum Res. 39, 209-217. [ Links ]
Kovac, M. & Groeneveld, E. 2008. VCE-6 user’s guide and Reference Manual Version 6. Biotechnical Faculty, Department of Animal Science, University of Ljubljana, Slovenia. [ Links ]
Mrode, R. A., Swanson, G. T. & Lindberg, C. M. 2002. Efficiency of part lactation test day records for genetic evaluations using fixed and random regression models. J. Anim Sci. 74, 189-197. [ Links ]
Muir, B. L., Fatehi, J., Schaeffer, L. R. 2004. Genetic relationships between persistency and reproductive performance in first-lactation Canadian Holsteins. J. Dairy Sci . 87, 3029-3037. [ Links ]
Muir, B. L., Kistemaker, G., Jamrozik, J. & Canavesi, F. 2007. Genetic parameters for a multiple-trait multiple-lactation random regression test day model in Italian Holsteins. J. Dairy Sci . 90, 1564-1574. [ Links ]
Pereira, R. J., Verneque, R. S., Lopes, P. S., Santana, J. L. S., Lagrotta, M. R., Torres, A. E., VercesiFilho, A. E. & Machado, M. A. 2012. Milk yield persistency in Brazilian Gyr cattle based on random regression model. Gene. Mole. Res. 11, (2), 1599-1609. [ Links ]
Rekik, B., BenGara, A., Ben Hamouda, M. & Hammami, H. 2003 Fitting lactation curves of dairy cattle in different types of herds in Tunisia. Live Sci.83,309-15. [ Links ]
Santos, D. J. A., Peixoto, M. G. C. D., Borquis, R. R. A., Verneque, R. S., Panetto, J. C. C. & Tonhati, H. 2013. Genetic parameters for test day milk yield, 305 -day milk yield, and lactation length in Guzerat cows. Live Sci . 152, 114-119. [ Links ]
Schaeffer, L. R. & Dekkers, J. C. M. 1994. Random regressions in animal models for test day production in dairy cattle. The 5th World Congress of Genetics Applied to Livestock Production, Guelph, Canada. [ Links ]
Shanks, R. D., Berger, P. J., Freeman, A. E. & Dickensen, F. N., 1981. Genetic aspects of lactation curves. J. Dairy Sci . 641, 1852-1860. [ Links ]
Solkner, J. & Fuchs, W. A. 1987. Comparison of different measures of persistency with special respect to variation of test day milk yields. Lives Sci. 16, 305-319. [ Links ]
Strabel, T., Kopacki, W. & Szwaczkowski, T. 2001. Genetic evaluation of persistency in random regression test day models. Interbull Bulletin 27, 189-192. [ Links ]
SAS, 2004. Statistical Analysis Users’ Guide, Version 9.1. SAS Institute Inc., Cary, North Carolina, USA. [ Links ]
Takma, C. & Akbas, Y. 2007. Estimates of genetic parameters for test day milk yields of Holstein Friesian herd in Turkey with random regression models. Arch Tierz . 4, 327-336. [ Links ]
Togashi, K. & Lin, C. Y. 2004. Efficiency of different selection criteria for persistency and lactation milk yield. J. Dairy Sci . 87, 1528-1535. [ Links ]
Togashi, K. & Lin, C. Y. 2006. Selection for milk production and persistency using eigenvectors of the random regression coefficient matrix. J. Dairy Sci . 89, 4866-4873. [ Links ]
VanRaden, P. M. 1998. Best prediction of lactation yield and persistency. The 6th World Congress Genetic Applied to Livestock Production. Armidale, Australia. [ Links ]
VanVleck, L. D. & Henderson, C. R. 1961. Estimates of genetic parameters of some functions of part lactation milk records. J. Dairy Sci . 44, 1073-1084. [ Links ]
Weller, J. I., Ezra, E. & Leitner, G. 2006. Genetic analysis of persistency in Israel Holstein population by the multitrait animal model. J. Dairy Sci . 89, 2738-2746. [ Links ]
Wood, P. D. P. 1969. Factors affecting the shape of the lactation curve in cattle. Animal Production 11, 307-316. [ Links ]
Yamazaki, T., Hagiya, K., Takeda, H., Sasaki, O., Yamaguchi, S., Sogabe, M., Saito, Y., Nakagawa, S., Togashi, K., Suzuki, K. & Nagamine, Y. 2014. Genetic correlation between milk production traits somatic cell scores on test day within and across first and second lactations in Holstein cows. Lives Sci. 152, 120-126. [ Links ]
Recibido: 21 de Febrero de 2018; Aprobado: 17 de Mayo de 2018











 text in
text in