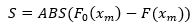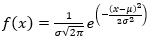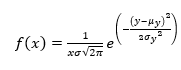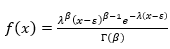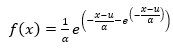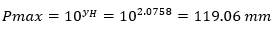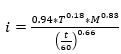Custom services
Spanish (pdf)
Article in xml format
Article references
Send this article by e-mail
Cited by SciELO 
Similars in
SciELO 
Permalink
Introducción
El análisis de los datos climatológicos cada día tiene más importancia ya que a partir del entendimiento del comportamiento de las variables relacionadas entre el clima y las actividades humanas a fin de aprovechar eventos como las precipitaciones, por ende evitar las consecuencias que pueden llevar las crecientes súbitas de los cauces y así, tal como lo afirman (Bazzano, et al., 2019) al hacer el análisis de datos de estaciones en períodos prolongados se puede evidenciar la tendencia al crecimiento en los fenómenos como la precipitación intensa lo cual presume un mayor riesgo de afectación a las rondas hídricas ocupadas desafortunadamente por asentamientos humanos.
Ahora bien, si es cierto e importante el análisis de datos basados en la cantidad de registros existentes en una zona y en la forma adecuada de la toma de datos, esto no significa que en todo el territorio nacional se den dichas condiciones, según el Instituto de Hidrología Meteorología y Estudios Ambientales en Colombia (2018), existen cerca de 4489 estaciones hidrometeorológicas de las cuales en su mayoría se encuentran en la región Andina, lo cual indicaría una alta presencia de mediciones en las diferentes fuentes de abastecimiento o cuencas a analizar, esto no se ve reflejado cuando se desea hacer estudios de precipitaciones en cuencas relativamente pequeñas o en las cuales no se encuentre alguna estación en la misma cuenca o se encuentren fuera de operación.
Una vez se entiende la realidad nacional y la distribución misma de las estaciones de medición, la forma en la cual se hacen los registros en ellas (automático o manual) es importante identificar la calidad de los datos, la continuidad de los mismos y la validez que puedan tener, en muchos casos de las estaciones no se conoce la información de registros en períodos de tiempo definidos por error en la toma o daños en los equipos lo cual puede llevar a registros nulos o incluso elevados, es allí donde es relevante el uso de herramientas de probabilidad y estadística como lo establecen que Barros & Turpo (2017); y Salazar Torres & Girón Cardenas (2021), donde emplean la identificación de las variables y definen algoritmos matemáticos programados para determinar y definir el comportamiento de dichas variables, esta aplicación es complementada por Lau, et al. (2021), donde emplean eficientemente el manejo de datos a través la gestión adecuada de la información por parte de los investigadores y permite un mayor compromiso con el seguimiento y gestión de los datos, el problema del proceso dentro de este producto fue el tiempo de ejecución del muestreo.
Partiendo de este último análisis es vital en todo manejo de información que los datos recopilados tengan un tiempo adecuado de registro porque de allí depende la precisión de los resultados obtenidos en el proceso de los mismos, en el caso de datos climatológicos como las precipitaciones o caudales los tiempos de registro de los datos dependen de la continuidad misma de los equipos y sitios de medición así por ejemplo (Jiao, et al., 2020) emplean series de datos de caudales del río Haihe entre los años 1960 a 1990 y de allí logran identificar un descenso en los niveles del río causado por actividades humanas en su rivera y también influenciado por el cambio climático.
Es claro que los datos pueden conseguirse con facilidad, el tema es el adecuado manejo dado a dicha información, usar estrategias matemáticas como la empleada por Hamdi, et al. (2015) , donde evalúan eventos climatológicos oceánicos extremos que pueden afectar a las plantas de producción de energía nuclear pero en el momento de hacer el análisis de los datos y determinar tanto los valores medios como la desviación estándar de los fenómenos encuentran datos demasiado alejados de las demás muestras de datos y por ende son retirados de la muestra y quedan únicamente como datos históricos poco repetidos o únicos, esto es comúnmente empleado en el análisis de datos debido a que dentro de la información sobre una variable pueden encontrarse valores los cuales difieren mucho de los valores medios y pueden afectar las predicciones al generar valores exagerados y puede conllevar a errores inducidos graves, la gestión y análisis debe incluir un detalle y comparación con varias fuentes de información o de criterios para poder retirar dichos datos desfasados sin afectar el proceso analítico de las variables.
Metodología
En el estudio desarrollado se obtiene una muestra de datos del Instituto de Hidrología Meteorología y Estudios Ambientales de la estación Páramo de Guerrero donde se tienen registros de precipitaciones máximas en 24 horas desde el período de 2005 a 2021, lo cual nos genera una muestra de datos continuos de 17 años de mediciones, una vez definida dicha estación de medición se encuentra un total de 6117 datos correspondientes desde el mes de enero de 2005 hasta el mes de septiembre de 2021, con estos datos de precipitaciones diarias se procede a definir las precipitaciones máximas por cada mes y luego por cada año para así reducir la muestra inicial a sólo 17 valores correspondientes a los datos de precipitaciones máximas mensuales en 24 horas anuales.
Una vez hecho este proceso se definen parámetros como la media, desviación estándar y varianza, es allí donde se evidencia la presencia de valores con desviaciones de la media muy grandes lo que indica posibles errores en la medición, a fin de hacer este manejo adecuadamente (Chow, et al., 1994) recomienda el método del Water Resources Council para los datos dudosos como se muestra:
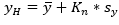para valores de datos dudosos altos
para valores de datos dudosos bajos
Donde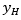 
es el valor del umbral máximo de los datos dados en la muestra y por ende 
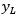es el valor del umbral mínimo, 
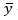es el valor de la media muestral, 
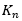corresponde al dato constante del método relacionado con la cantidad de valores dentro de la muestra y se usan en pruebas para detectar datos dudosos en el 10% de significancia en información normalmente distribuida y 
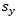corresponde a la desviación estándar, tanto el valor de 
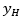como el de 
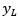con los exponentes correspondientes a una base 10 y con la expresión se define el valor máximo y mínimo de la muestra así (E1):
(E1)
Posterior a este proceso y una vez determinados los valores a trabajar dentro de la muestra para cada uno de los 17 años de registros, es necesario verificar los ajustes de distribuciones de probabilidad por diferentes funciones y hacer pruebas de bondad de ajuste de los datos así como Gálvez-Nieto, et al. (2017), se emplean en sus estudios la bondad de ajuste de Chi cuadrado mediante la expresión (E2):
(E2)
Donde m es el número de intervalos, es el valor de la frecuencia relativa en el intervalo i, es el valor teórico esperado y para determinar la bondad de ajuste es necesario definir la sumatoria de estas relaciones en cada uno de los intervalos a los cuales se ajustan los datos, esta cantidad de intervalos en los que se debe repartir la muestra se define mediante la expresión (E3):
(E3)
Donde NC es el número de intervalos y N es la cantidad de datos muestrales.
Para la validez de la prueba de Chi cuadrado es necesario que se contraste y verifique con los grados de libertad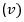 
y el nivel de confianza 
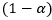mediante la expresión (E4):
(E4)
m es el número de intervalos, p es el número de parámetros empleados en la distribución y es el nivel de significancia donde generalmente se adopta como el 5% si se desea tener un grado alto de ajuste de los datos o valores porcentuales mayores acorde a las necesidades de cada estudio.
Otra prueba de bondad de ajuste empleada extensamente es la de Kolmogorov - Smirnov usada por Khrueasom & Pongpullponsak (2017); y Vargas, et al. (2019), a fin de establecer un mejor control en los procesos de mantenimientos y fabricación para la reducción de costos productivos, esta prueba de ajustes en los datos se define a partir de la hipótesis de validez que se plantea desde la diferencia absoluta entre la probabilidad de ocurrencia del dato medido 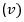y la probabilidad esperada 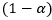acorde a la distribución de probabilidad elegida mediante la siguiente expresión (E5):
(E5)
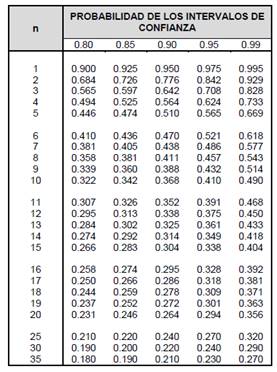
Para valorar entonces el nivel de ajuste es necesario también definir como en la prueba de bondad de ajuste de chi cuadrado el nivel de confianza esperado en la muestra y claramente determinar a su vez el número de intervalos, con este dato se establece con la siguiente tabla el valor a tomar como dato crítico (Figura 1):
Manual de drenaje para carreteras.
Con la representación anterior se establece el valor crítico y se compara con el valor de S calculado, si S<C el ajuste de este método es correcto, de ser de diferente manera se rechaza el ajuste de los datos a la distribución ensayada.
Complementando lo anteriormente mencionado las distribuciones de probabilidad que se pueden emplear en estudios de este tipo son Normal, Log Normal, Pearson lll, Log Pearson lll, Gumbel y Log Gumbel como se describen a continuación:
Su uso está dado ampliamente en la literatura con diferentes aplicaciones a variables continuas donde se permite evidenciar el comportamiento de dichas variables hacia una zona central y observar a los valores ubicarse allí y son simétricos a partir del valor medio tal como es analizado por Aljohani (2022), donde se valora la percepción del ruido y su comportamiento en forma de ondas y como la percepción del ruido se ajusta a dicha distribución en forma de campana concéntrica y que hacia sus laterales es simétrica y desciende de forma curva y emplea la expresión en su forma general (E6):
(E6)
Distribución Log Normal
Esta distribución es la que más se presenta en fenómenos de la naturaleza según Andersson, (2021) debido al ajuste adecuado para simular las condiciones de diferentes fenómenos en la naturaleza y su comportamiento, tal como las emisiones de CO2 y como pueden variar por su concentración en la atmósfera con la influencia de otros fenómenos, la modelación de dicha distribución de probabilidad se emplea la expresión (E7 ):
(E7)
Donde y= log x
Distribución Pearson lll
También conocida como gamma de tres parámetros es una función empleada para describir variables asimétricas sin el uso de una transformación logarítmica y, como lo describe Muñoz (2014), la distribución gamma debe su nombre a la función del mismo nombre y además se relaciona con la distribución de Poisson dentro de la expresión (E8):
(E8)
Distribución Log Pearson III
Así como la distribución log normal, la distribución log Pearson lo que hace es relacionar los datos al sacarle el logaritmo para mejorar la tendencia de los mismos, la expresión general de dicha distribución es (E9):
(E9)
Donde y= log x
Distribución de Gumbel
Esta distribución también tiene una forma curvada de forma asimétrica y es empleada comúnmente para caracterizar fenómenos naturales como lo establecen Wang, et al. (2021), al identificar el comportamiento de las tormentas que afectan a la zona de la península de Shandong en china y el cual se ajusta adecuadamente a dicha distribución, se modela con la siguiente ecuación (E10):
(E10)
Distribución Log Gumbel
Tal como las expresiones previas, lo que se busca con una distribución log gumbel es generar un mejor ajuste de los datos aplicando el logaritmo a los mismos para mejorar su comportamiento hacia la distribución de probabilidad y se establece de la siguiente manera (E11):
(E11)
Una vez verificado el ajuste de los datos se procede a determinar la curva intensidad - duración - frecuencia con la metodología empleada por Pérez Rodríguez (2019), donde se aplica una forma simple y de forma sintética la obtención de una ecuación con la cual se predice las posibles lluvias que puedan ocurrir con diferentes períodos de retorno mediante la expresión (E12):
(E12)
Donde:
I = |
intensidad de la lluvia o precipitación de diseño a, b, c y d son los coeficientes determinados por Díaz & Vargas (1997), para cada región en Colombia |
T= |
período de retorno de las lluvias bajo recomendación de diseño |
M = |
valor máximo anual de precipitación diaria |
t= |
duración de la lluvia en tiempo de concentración |
Así como existe esta expresión para Colombia existen muchas más expresiones como las mencionadas por Hadi Mahdi (2020); tales como la expresión de Talbot, Bernard, Sherman y Kimijima donde por medio de métodos de regresiones y con la cantidad de datos suficientes se pueden hacer los estimativos de sus parámetros de ajustes y como lo definió en su estudio se pueden aproximar cada una de las expresiones según el ajuste de probabilidad y generar comparaciones entre sí, cada expresión y cada ajuste otorga parámetros diferentes acorde al registro de datos y a la cantidad de los mismos.
Resultados y discusión
Para la estación denominada “Páramo de Guerrero” ubicada en el municipio de Zipaquirá, Cundinamarca, Colombia se procede a desarrollar el análisis de datos que según el Instituto de Hidrología, Meteorología y estudios ambientales (2018), en Colombia, en las estaciones las mediciones de precipitaciones son establecidas de manera continua a través de pluviómetros y pluviográfos, en el presente desarrollo se toman los datos de precipitaciones máximas en 24 horas durante un período de 17 años, de estos 6117 datos se empiezan a definir características de distribución de los datos como se muestra (Figura 2)
De la figura 2 se puede observar que el dato inicial en la medición como valor máximo de precipitación en el año 2005 es de 227.8 mm, dentro de la muestra se tiene también un valor medio de 44.435 mm lo cual evidencia a este dato con alta variación del valor medio, esto se refleja en la varianza al tener un valor de 2275.289 con una desviación estándar de 47.69 mm, ese dato corresponde al primer año y primer mes de operación de la estación del año y se encuentra por encima del valor máximo de precipitación estimado para el umbral superior dado por la expresión (E13):
(E13)
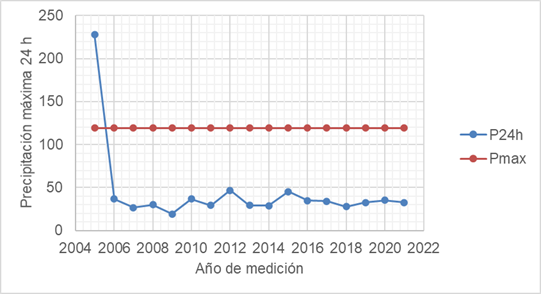
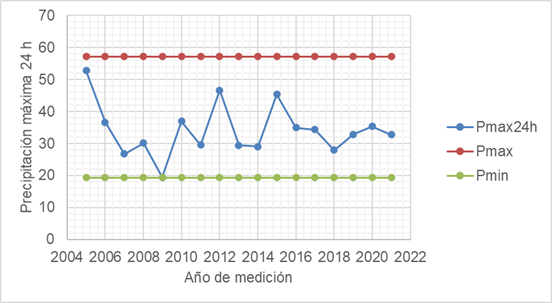
Con este valor de precipitación máxima esperada dentro de la muestra se procede a retirar la lluvia que se encuentre por encima de este valor y se recalculan los valores de media, varianza y desviación estándar hasta el momento en el cual los datos ajustados posteriores a la eliminación de cada dato estén por debajo del umbral máximo, es decir, se hace un reprocesamiento cada vez que se retira un valor dudoso y a consecuencia de esto cambia la media, la varianza y la desviación estándar de los datos, en este caso puntual se retiraron 25 datos los cuales se encontraban por encima del umbral máximo y se debió de hacer esa misma cantidad de veces el proceso para lograr definir un umbral máximo final Pmax de 57,1 mm de precipitación, con media de los datos de 34,14 mm, una varianza de 65.65 y una desviación estándar de 8.1 mm, resultado de este ajuste y manipulación de los datos se obtiene la figura 3:
Dentro de la aplicación de la bondad de ajuste por medio de Kolmogorov - Smirnov se hacen ajustes a distribuciones de probabilidad Normal, Log Normal, Pearson lll, Log Pearson lll, Gumbel y Log Gumbel a fin de verificar con dichas distribuciones de probabilidad el mejor ajuste posible a los datos medidos en la estación objeto de análisis, este proceso se hace mediante herramienta de Excel y los resultados se resumen en la siguiente tabla:
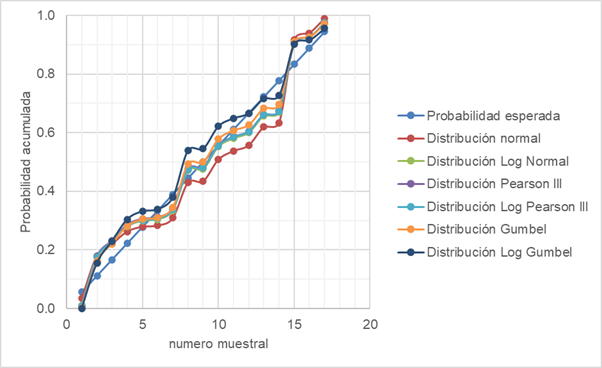
Fig. 4 - Validación gráfica de la bondad de ajuste de los datos por las 6 funciones de distribución de probabilidad.
De la figura 4 se puede inferir que cada una de las funciones de probabilidad analizadas tienen un ajuste adecuado hacia la tendencia de los datos al tener todo un valor de ajuste adecuado al satisfacer la condición de confianza en el ajuste de los datos cuyo valor debe ser siempre menor a 0.318, este valor no es superado en ninguna de las distribuciones analizadas así que la hipótesis de ajuste es válida para todas.
En la determinación de la curva de intensidad - duración - frecuencia sintética se parte desde el proceso mencionado previamente y al tomar los valores de las constantes a, b, c y d se obtiene la expresión final (E14):
(E14)
Con esta expresión definida se procede a determinar con diferentes períodos de retorno sus correspondientes duraciones de lluvias y las intensidades calculadas para la estación de Páramo de Guerrero (figura 5):
Fig. 5 - Curvas de intensidad - duración - frecuencia para diferentes períodos de retorno en años, duraciones de lluvia en minutos e intensidades de lluvia en mm/h.
Como resultado de este proceso de análisis de datos se obtienen tanto la expresión propia de la estación analizada así como su curva IDF con la cual se pueden hacer las estimaciones de lluvias esperadas en cualquier período de retorno con la duración que se pueda estimar consecuente con los tipos de análisis a desarrollarse en el municipio de Zipaquirá, Cundinamarca.
Conclusiones
El ajuste de datos dudosos es necesario para esta estación debido a que los valores medidos al inicio de su operación tienen valores superiores a los 57.19 mm de precipitación diaria y fue superado en 22 días seguidos con registros elevados de precipitación cercanos a 100 mm o incluso tiene un máximo valor de 227.8 mm lo cual es casi 4 veces mayor que ese valor de umbral máximo ajustado.
La distribución de Gumbel es la mejor ajustada a los datos una vez hecha la prueba donde se hace la diferencia entre la probabilidad de ocurrencia del dato medido y la probabilidad esperada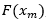 
, para este caso esta diferencia su valor máximo es de 0.0821, número muy por debajo del valor de 0.318 e indica que el ajuste es muy bueno bajo esta condición de distribución.
Una vez determinada la curva IDF de esta estación se pueden desarrollar diseños basados en precipitaciones en la zona de influencia de la estación al tener en cuenta que se puede estimar lluvias para hacer diseños de recolección de la misma, optimización del recurso en los períodos de sequía, prevención de inundaciones, etc. esto puede migrarse a cualquier estación del país al seguir la misma metodología y al corroborar la confiabilidad de los datos con el fin de mejorar la estimación de la precipitación calculada.
Una vez se tienen este proceso se continua con la investigación y se proyecta diseñar un sistema de predicción de lluvias donde los usuarios puedan hacer consultas puntuales sobre alguna fecha en específico y la probabilidad de ocurrencia de una precipitación; así como el valor estimado para dicha lluvia.
El potencial de aplicación de este proyecto dependerá también de la calidad de los datos y de los registros continuos que toma la estación, se puede mejorar este resultado con mejor precisión con el paso del tiempo y la estación Páramo de Guerrero registra más datos de precipitaciones a fin de tener una muestra más amplia y se puedan tomar las condiciones de climas variables en períodos más largos con lo cual se pueden hacer mejores estimaciones para períodos de retorno más prolongados en función de los diseños de obras civiles con tiempos de duración de 50 años o incluso más.
