Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Ciencias Informáticas
versión On-line ISSN 2227-1899
Rev cuba cienc informat vol.7 no.2 La Habana abr.-jun. 2013
ARTÍCULO DE REVISIÓN
Métodos clásicos de nicho para optimización multimodal: una breve revisión
Classical niching methods for multimodal optimization: a brief review
Ricardo Navarro 1*, Gonzalo Nápoles 2
1 Informatics Department. University of Hoguín, Avenue XX Aniversario, s/n, Reparto Piedra Blanca, Holguín, Cuba. CP.: 81000. *E-mail: rnavarro@facinf.uho.edu.cu
2 Computer Sciences Department. Universidad de Las Villas, Carretera a Camajuaní, km 5½, Santa Clara, Villa Clara, Cuba, CP:54830 E-mail: gnapoles@uclv.edu.cu
RESUMEN
En las últimas dos décadas los métodos poblacionales de optimización han sido muy usados por su capacidad para encontrar buenas soluciones con un esfuerzo bajo, convergiendo a un único óptimo global. En muchos problemas prácticos, multimodales por naturaleza, es importante hallar varias soluciones óptimas, sean locales o globales. Los métodos de nicho permiten ubicar múltiples soluciones al mantener diversidad entre los individuos de la población. En este trabajo son abordados los métodos clásicos de nicho para optimización multimodal. Además, se discuten las principales limitaciones de estas técnicas y se presentan aspectos a considerar cuando se analiza su comportamiento.
Palabras clave: algoritmo evolutivo, especiación, nicho, optimización multimodal.
ABSTRACT
In last two decades population based optimization methods has become widely used since their capability to find good solutions with a low effort by converging to a single global optimum. Many real-world problems are multimodal by nature, being very important to find all optimal solution, may it be local or global ones. Niching methods allow locating multiple solutions since they are capable to maintain the diversity among the individuals on the population. In this work an approach to classical niching methods for multimodal optimization is made. Main drawbacks in such strategies are also discussed while useful topics on the performance analysis of these techniques are presented.
Key words: evolutionary algorithm, niching, multimodal optimization, speciation.
INTRODUCCIÓN
Population based algorithms are an efficient alternative for solving hard optimization problems. Despite they are capable to find high quality solutions these algorithms typically converge to a single final solution due to their global selection scheme. However, problems from multiple domains such as structure recognition, economic modeling and engineering design, are highly multimodal. The main goal of multimodal optimization is to locate several optimal solutions, may them be global or local, and then to choose the most appropriate solution considering practical issues. When dealing with multimodal problems some modifications to standard population based algorithms are needed, in order to provoke the formation of stable subpopulations (also known as niches) at all peaks in the search space.
Niching methods appear from the analogy with natural ecosystems, which are often composed by different physical spaces (niches) that allow the formation and the maintenance of distinct types of life competing to survive (species). A species is then formed by agents biologically similar, which are able for interbreed, but not with any from other species. For each niche the physical resources are finite and must be shared among its individuals (Sareni, 1998).
By analogy, niching promotes genetic diversity by emerging different sub-populations (niches), each corresponding to an optimum (peak) of the domain. The fitness represents the resources (carrying capacity) of the niche, while species can be defined as similar individuals in terms of certain measures. Speciation methods have been introduced in evolutionary algorithms (EA) to save diversity among individuals by forming and maintaining stable subpopulations (Cedeño, 1999). It is required to conserve highly fit individuals and also those that are different enough from them to be worth keeping. The result is an algorithm that maintains solutions in multiple peaks while allowing a subset of individuals to explore other regions of the search space. Without niching strategies, a population based algorithm generally concentrates on the best peak found so far (Bird, 2006), while otherwise the algorithm searches for multiple solutions at a time. Even on problems with a single global solution, this has benefits as reducing the risk of the method sticking locally; some agent will exploit the optimum, but others will explore other areas of the search space.
In the next section a brief review on niching methods is given. Despite it is focused on the classical techniques, more recent ones are approached or mentioned as well. Section 3 summarizes main limitations of most niching methods while useful aspects on their performance analysis are detailed in section 4. Finally, conclusions are presented.
Briefly surveying niching methods
Many niching methods have been reported in the EA literature. One of the first was Cavicchio’s pre-selection (Mahfoud, 1992), later generalized in crowding (De Jong, 1975). The sharing concept, introduced in (Holland, 1975), was used (Goldberg, 1987) to ease the selection pressure caused by the fitness proportionate reproduction (FPR) rule (Holland, 1975). The deterministic crowding (Mahfoud, 1992) deals with it by letting agents to mate with any other, while in restricted tournament selection (RTS) (Harik, 1995) it is done by modifying the selection and replacement steps of the steady state genetic algorithm (SSGA). Fitness derating (Beasley, 1993) allows unimodal optimization methods deal with multimodality by using the knowledge gained in a run to avoid re-searching the same area.
Other illustrative examples are clearing (Pétrowski, 1996) and clustering (Kennedy, 2000). Niching principles have also been applied to Particle Swarm Optimization (PSO), such as NichePSO (Brits, 2002) and SPSO (Parrott, 2006), as well as to Differential Evolution (DE), including the species-based DE (SDE) (Li, 2005) and Differential Evolution with an ensemble of Restricted Tournament Selection (ERTS-DE) (Qu, 2010). Furthermore, they have addressed combinatorial optimization problems (Nagata, 2006 and Yang, 1998) and multi-objective ones as well (Chen, 2006 and Kowalczuk, 2006). Research community on niching methods has dedicated great efforts to devise niching techniques in absence of parameters derived from a priori knowledge about the fitness landscape, like the lbest PSO niching algorithms using a Ring Topology (Li, 2010) and the Adaptive Species Discovery (ASD) (Della Cioppa, 2011) as well. Other strategies have been devised to automatically estimate effective values for such parameters, for instance the Adaptive Niching PSO (ANPSO) (Bird, 2006) and the CMA-ES niching algorithm (Shir, 2006). Since their large variety, describing most niching methods is out of the scope of this work. Instead, basic principles of some of the ones mentioned above which are classical approaches and other relevant methods are presented below. Chart 1
Crowding
Crowding was first designed only to keep population diversity since it inserts new elements in the population by overwriting similar ones. In the basic scheme only a fraction of the global population (generation gap) reproduces and dies at each generation. It is, an offspring is compared to a small random sample taken from the current population and the most similar individual there is replaced. The crowding factor (CF) parameter is often used to determine the size of the sample. This CF model is analyzed in (Mahfoud, 1992) and attributed its inability to maintain more than two peaks of a multimodal landscape to stochastic errors in replacement which create genetic drift and fixation.
Deterministic crowding
Mahfoud made successive changes to crowding to reduce replacement errors, restore selection pressure and eliminate the crowding factor, resulting the deterministic crowding (Mahfoud, 1992), which is able to locate and maintain multiple peaks by competition between children and parents of equal niches. After crossover and mutation, each child replaces its nearest parent if it has a higher fitness. The procedure in Chart 2 is to be performed N/2 times (N is the population size) and the overall process is to be repeated g generations. d is the phenotypic distance between agents.
Probabilistic crowding
When a deterministic tournament is used crowding methods will always prefer higher fitness agents over lower fitness ones, thus leading to a loss of niches whenever the tournaments between global and local niches are played. To avoid this deterministic nature and hence to provide a restorative pressure in such cases, it was proposed the probabilistic crowding (Mengsheol, 1999). Here, a probabilistic replacement rule was used to permit higher fitness individuals to win over lower fitness individuals in proportion to their fitness. The method is essentially the deterministic crowding with a probabilistic replacement operator. Two similar individuals X and Y compete, being the probability of X to win:
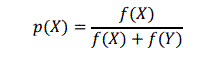 (1)
(1)
Multiniche crowding genetic algorithm
In a further approach, the multiniche crowding genetic algorithm (MNC GA) illustrated in Chart 3, both selection and replacement are modified by some kind of crowding to deal with the selection pressure caused by FPR and allow the population to keep diversity. No prior knowledge of the problem is needed and no restriction affects selection neither replacement. The MNC GA uses a replacement policy called worst among most similar (WAMS). Chart 4 shows a view of this replacement policy (Cedeño, 1999).
Fitness sharing
Fitness sharing (FS) is maybe the most common niching method (Sareni, 1998). It was moved by nature, where an individual has only limited resources to be shared with other ones in the same niche. Introduced in (Holland, 1975), it was used in (Goldberg, 1987) to part the population into various subpopulations by the similarity of the individuals.
Typically, the shared fitness fsh(i) of an individual i is its raw fitness f(i) divided by its niche count:
N denotes the population size and d(i,j) is a distance measure between the individuals i and j. The sharing function (sh) computes the similarity between two individuals. The most used is described above, where σsh (niche radius) is a threshold of dissimilarity and α (scaling factor) is a constant that regulates the shape of sh. Distance is based on a genotypic (Hamming’s) similarity metric or a phenotypic (Euclidean) one. Sharing based on phenotypic one may give slightly better results (Deb, 1989). Despite its proven value, it has several difficulties, being the main not to be easy to set proper values for σsh and α without prior knowledge of the problems.
Dynamic niche sharing
Beyond the classic sharing there are many tries, dynamic niche sharing (DNS) (Miller, 1996), to self detect niches by using this scheme. DNS adopts a dynamic species identification and partitions the population by assuming that the number of niches of the fitness landscape is a priori known. Thus, DNS defines a fixed number of dynamic niches with radius and centers determined by a full population sort. The individuals not belonging to any of the previously identified species are grouped into a unique nonspecies class.
Moreover, the fitness of the individuals is modified according to two different sharing mechanisms. The shared fitness of an individual belonging to a species is computed by dividing its raw fitness by the occupation number of the niche. However, for those individuals not in a niche, regular fixed sharing is used, in that the standard fitness sharing formula is used for individuals belonging to the nonspecies class. The authors motivate this choice in terms of computational cost, as the occupation number is computed only once for all the individuals of a species, while the niche count has to be computed for each individual in the population. It presents certain advantages over other nichers. However, as this method requires an estimate of the number of peaks in addition to the niche radius, its primary weakness is the use of fixed sharing outside the dynamic niches (Goldberg, 1997).
Implicit fitness sharing
In the implicit fitness sharing (Smith, 1993) each individual’s fitness is functionally dependent on the rest of the population. Sharing is done by inducing competition for limited and explicit environmental resources. For each resource, a set of individuals is randomly selected from the population and each one is matched against the resource.
The individual with the highest score is then rewarded. Such a procedure is repeated a given number of times, through which the score of individuals is updated. At each generation, the discovered niches are obtained by selecting the minimal set of individuals needed to match all the resources. Therefore, niching is implicit in that the number of peaks is determined dynamically and there is no specific limitation on the distance between peaks.
Hence, it is avoided the difficulty of appropriately choosing the niche radius and the method may to deal with problems in which the peaks are not equally spaced. This method introduces other parameters to be set; it is the size of the sample of individuals that compete, the number of competition cycles and the definition of a matching procedure. Moreover, it can be applied, at best, on problems in which explicit and finite resources are available.
Dynamic fitness sharing
Dynamic fitness sharing (DFS) (Della Cioppa, 2007) is another attempt to automatically identify the niches in the population during the evolution. As shown in Chart 5, it is based on a dynamic explicit identification of the species.
Coevolutionary sharing
The coevolutionary sharing model (Goldberg, 1997) attempts to avoid the estimation of niche radius. It uses two coevolving populations: customers and businessmen. Customers are served by the nearest businessman. By using a sharing function, customer fitness is derated in proportion to the total number of other customers served by the nearest businessman. Thus, there is pressure to find businessmen serving relatively few customers.
The customer evolves under a traditional GA. In contrast, the businessmen attempt to maximize the number of customers served, having more customers yields higher fitness. To prevent convergence of the businessmen to a single global optimum, they are separated at least by a distance dmin. This population evolves by a mechanism that converts the best customers into businessmen. For each businessman, n customers are randomly selected. The first customer that is both more fit than it and at dmin away from other businessmen, replaces the original businessman.
Sharing via niche identification techniques
A sharing scheme based on niche identification techniques (NIT) is proposed in (Lin, 2002). It is capable of determining the center location and the radius of each of existing niches based on fitness topographical information of designs in the population. Genetic algorithms with NIT were compared to GAs with traditional sharing scheme and sharing with cluster analysis methods. Results of numerical experiments showed that the sharing scheme with NIT improved both search stability and effectiveness of locating multiple optima.
Clearing
The clearing procedure (Pétrowski, 1996) is alike fitness sharing. If an individual belongs to a given subpopulation, then its dissimilarity with the dominant (individual with the best fitness) is less than a given threshold σ (the clearing radius). Instead of evenly sharing the resources among the individuals of a sub-population as in fitness sharing, clearing attributes them only to the best members (the winners) of each sub-population. Its reliability is similar to that of the sharing method with lower complexity but, like sharing, it requires a priori knowledge of the niche radius.
Pseudo code of a simplified version of the clearing procedure is presented in Chart 6, where population P is seen as an array of N agents, the capacity (κ) is the maximun number of winners that a niche can accept, while nbWinners is the number of winners of the subpopulation associated with the current niche. Clearing allows dosing the niching effect between the maximum capacity (κ = 1) and its absence (κ = N). Its major weakness is the need for estimate σ (Sareni, 1998), while a great assets is that its complexity is O(C N) (being C the number of peaks) instead of sharing’s O(N 2).
Fuzzy clearing
While in standard clearing an individual dominates those within a range σ, in a further approach (Sacco, 2004) the individuals were clusterized before submitting them to clearing, dominance is seen within a cluster. Each individual is allotted solely to a single cluster by the KMEAN adaptive algorithm. Since it classifies in a deterministic way, being far from ideal in functions with unknown behavior or several nearby optima, in real world problems it has a high degree of uncertainty. The use of fuzzy logic to clusterize the individuals naturally appears. Thus, they used as fuzzy class separation algorithm the fuzzy clustering means (FCM). It uses the concept of pertinence that denotes the degree of association of an individual to a given class. Authors made a combination of an efficient niching technique with a clustering method free of previous knowledge of the problem. A pseudo code to be applied after clustering is shown in Chart 6.
Genetic Algorithm with Sharing and Fuzzy Clustering
With fuzzy clustering, in the Genetic Algorithm with Sharing and Fuzzy Clustering (GASH-FC) (El Imrani, 2000), the number of niches is automatically determine by continuously updating the radius of each niche until finding an optimal solution. It is a three-layer strategy (Chart 7) that can be seen as a generalization of hard clustering, with the gain of efficiently dealing with overlapping clusters. Each cluster represents a niche while their centers correspond to the desired optima. As this method uses a self-learning procedure, the number of clusters (C) is computed by itself. Niches merge by using the center and the radius of each cluster while a GASH handles the evolution of each sub-population to identify a non-found niche in the previous iteration.
Sequential niching
Sequential niching (Beasley, 1993) works by iterating a simple GA and maintaining the best solution of each run off-line. To avoid converging to the same area of the search space multiple times whenever a solution is located it depresses the fitness landscape at all points within some radius of that solution. This ensures that on subsequent runs the same peak will not be rediscovered. This technique has many similarities with fitness sharing. However, instead of the fitness of an individual being reduced because of its proximity to other members of population (sharing), individuals have their fitness reduced because their proximity to peaks located in previous runs. This approach suffers similar limitations about choosing appropriate values for the niche parameters.
Species conserving genetic algorithms
The species conserving genetic algorithms (SCGA) (Li, 2002) evolve parallel subpopulations by using species conservation. According to their similarity, population is divided into several species, each of which is built around a dominating individual (the species seed). Species seeds found in the current generation are saved to the next one.
The definition of a species and the operation of the SCGA depend on the species distance (σs), the upper bound on the distance between two individuals for which they are considered to be similar. This parameter determines which individuals are worth preserving from one generation to the next. The distance between any two individuals in a species is less than σs while any two individuals within a distance less than σs are not forced to be in the same species.
The algorithm builds Xs (the set of species found in generation t) by successively considering each individual in t, in decreasing order of fitness. Considering an individual means it is compared to the current species seeds. If Xs does not contain any seed that is closer than half the species distance (σs/2) to the individual considered, then the individual will be added to Xs. Once all the species are found the new population is constructed by applying the typical genetic operators. Since some species might not survive after such operations, they are directly saved to the new population.
Relevant drawbacks of niching algorthims
Near all these methods depend on parameters usually hard to set as such prior knowledge is often unavailable in real-world problems. Many tries to deal with such drawback are reported (Bird, 2006 and Shir, 2006). In addition, most niching methods perform poorly when the dimensionality of the problem or the number of optima increases, while for some ones it is hard to maintain found solutions. Also, some niching techniques only play to find all global optima, while ignoring local ones.
Furthermore, a regular drawback is the high computational complexity. As regards this, sharing has a complexity of O(N 2), being N the population size. Clearing has a complexity of C x N, where C is the number of subpopulations. For RTS it is w x N,being w the window size (its niching parameter) and for DFS it is between O(N) and O(N 2). With O(N), both deterministic and probabilistic crowding are the less complex among methods included in this work.
On the performance evaluation of niching methods
The behavior of niching methods is assessed by analyzing specific measures over the optimization process of well known benchmark multimodal functions. Some topics on both functions and measures are presented next.
Test functions
While illustrative multimodal benchmark problems widely studied as M1, M2 and M6 are presented, further examples can be found in (Della Cioppa, 2011; El Imrani, 2000; Li, 2005; Qu, 2010 and Sareni, 1998). Chart 8
M1 and M2 were firstly proposed in (Goldberg, 1995) and are the simplest among the ones proposed in the literature for studying the behavior of a niching method. The aim in using such functions is particularly devoted to analyze the ability of the method to maintain the discovered niches rather than its searching ability. M1 is defined as follows:
![]()
It has five peaks at x=0.1, 0.3, 0.5, 0.7 and 0.9 all with a height equal to 1.0. M2 is the same than M1 regarding the optima values but the heights of the peaks are x=1.0, 0.917, 0.707, 0.459 and 0.250 respectively. It is defined as:
![]()
M6 (Shekel's Foxholes) was firstly introduced in (De Jong, 1975). Although not deceptive, it is more complex than the previous. The independent variables range in [-65.536,65.535] and its 25 equidistant peaks are located in correspondence of the coordinates [16i,16j], where i and j are integer variables ranging in the interval [-2,2]. The peaks heights range in [476.191,499.002] and the highest peak is located at (-32,32). Its analytical form is:
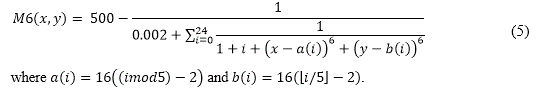
Performance criteria
When assessing niching methods, different criteria concerning with their ability to identify the optima might be used. Perhaps the most widely used criteria is the effective number of peaks maintained (in literature ENPM or EPM), that means the ability of a method to locate and maintain individuals at peaks for long periods of time. It is often just tracked the number of peaks maintained as a function of the number of evaluations run (Sareni, 1998). The maximum peaks ratio (MPR) is also commonly used. It gives both the quality and the number of the optima reached:
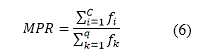
where Fi is the fitness of identified optimum i and fk is the fitness of the actual optimum k. C is the number of reached peaks, which contain the identified optima, and q is the number of real optima. An optimum is as detected if its fitness value is at least 80% of the actual. Besides, some authors (Sareni, 1998) also check that the optimum is within a niche radius of the real optimum. If not found, the local optimum value is set to zero. Hence, the top value for the MPR is 1.
Other criteria (Della Cioppa, 2011; El Imrani, 2000; Li, 2005 and Sareni, 1998) are the ENPM and MPR saturation values (GE and GM respectively), that reveal the generations after which the 99% of such saturation values are reached; the number of fitness function evaluations (NFE) required for the population convergence; the accuracy, which gives the proximity of fittest solutions to all actual optima; the convergence speed, that measures the number of evaluations needed to reach certain accuracy; the success rate, meaning the percentage of runs in which all optima are successfully located and the chi-square-like deviation, that reveals the method’s ability to evenly populate the niches.
CONCLUSIONES
Since the large the number of niching techniques is, after presented some relevant issues about basics of multimodal optimization, niching methods are briefly surveyed. It regards classical ones, including fitness sharing, crowding, clearing and clustering; extensions to previous methods are presented as well. It must be noted that there is still a need for devise methods out of niching parameters, which is maybe the most regular difficulty in such methods.
Moreover, nearly all niching techniques have a low performance when either the dimensionality of the search space or number of the optima increases. Besides, it is often hard to maintain found solutions along generations; whereas some niching approaches only search for locating all global optima, while ignoring local optima.
Conversely, some real domains demands to obtain both global and local optima at a time. Also, the frequent estimation of information from the whole population requires around O(N 2) computational complexity. All reported drawbacks define the current and future research lines on niching methods. Finally, they are presented some benchmark functions from multimodal problems test suite while main criteria used when assessing the performance of niching methods are also depicted.
REFERENCIAS BIBLIOGRÁFICAS
BEASLEY D., BULL D. R. and MARTIN R. R. A Sequential Technique for Multimodal Function Optimization. Evolutionary Computation, 1993, 1(2), 101-125.
BIRD S. and LI X. Adaptively Choosing Niching Parameters in a PSO. In Proceedings of the 8th Genetic and Evolutionary Computation Conference (GECCO’06). Seattle, Washington: 2006, p. 3-9.
BRITS R. and VAN DEN BERGH F. A Niching Particle Swarm Optimizer. In Proceedings of the 4th Asia-Pacific Conference on Simulated Evolution And Learning (SEAL’2002). Singapore: 2002, p. 692-696.
CEDEÑO W. and VEMURI V. R. Analysis of Speciation and Niching in the Multi-Niche Crowding GA. Theoretical Computer Science, 1999, 229, p. 177-197.
CHEN T. Y. and HSU Y. S. A Multiobjective Optimization Solver Using Rank-Niche Evolution Strategy. Advances in Engineering Software, 2006, 37, p. 68-699.
EB K. and GOLDBERG D. E. An Investigation of Niche and Species Formation in Genetic Function optimization. In Proceedings of the 3rd Internationl Conference on Genetic Algorithms. Ed. Morgan Kaufmann, 1989, p. 42-50.
DE JONG K.A. An Analysis of the Behaviour of a Class of Genetic Adaptive Systems. Doctoral dissertation, University of Michigan, Ann Arbor, MI, 1975.
DELLA CIOPPA A., DE STEFANO C. and MARCELLi, A. Where Are the Niches? Dynamic Fitness Sharing. IEEE Transactions on Evolutionary Computation, 2007, 11(4), p. 453-465.
DELLA CIOPPA A., MARCELLI A. and NAPOLI P. Speciation in Evolutionary Algorithms: Adaptive Species Discovery. In Proceedings of the 13th Genetic and Evolutionary Computation Conference (GECCO’11). Dublin, Ireland: 2011.
EL IMRANI A., BOUROUMI A., ZINE EL ABIDINE H., LIMOURI M. and ESSAÏD A. A Fuzzy Clustering-Based Niching Approach to Multimodal Function Optimization. Journal of Cognitive Systems Research, 2000, 1, p. 119-133.
GOLDBERG D. E. and RICHARDSON J. Genetic Algorithms With Sharing for Multimodal Function Optimization. In Proceedings of the 2nd International Conference on Genetic Algorithms. Hillsdale, NJ: L. Erlbaum Associates Inc., 1987, p. 41-49.
GOLDBERG D. E. and WANG L. Adaptative Niching via Coevolutionary Sharing. In Genetic Algorithms in Engineering and Computer Science. New York: Wiley, 1997, p. 21-38.
HARIK G. R. Finding Multimodal Solutions Using Restricted Tournament Selection. In Proceedings of the 6th International Conference on Genetic Algorithms. Eshelman L.J., Ed. Morgan Kaufmann, 1995, p. 24-31.
HOLLAND J. H. Adaptation in Natural and Artificial Systems. The University of Michigan Press, Ann Arbor, MI, 1975.
KENNEDY J. Stereotyping: Improving Particle Swarm Performance with Cluster Analysis. In Proceedings of the IEEE International Conference on Evolutionary Computation. 2000, p. 303-308.
KOWALCZUK Z. and BIAŁASZEWSKI T. Niching Mechanisms in Evolutionary Computations. International Journal of Applied Mathemathics and Computater Science, 2006, 16(1), p.59-84.
LI J. P., BALAZS M. E., PARKS G.T and CLARKSON P. J. A Species Conserving Genetic Algorithm for Multimodal Function Optimization. Evolutionary Computation, 2002, 10(3), p. 207-234.
LI X. Adaptively Choosing Neighbourhood Bests Using Species in a Particle Swarm optimizer for Multimodal Function Optimization. In Proceedings of 6th Genetic and Evolutionary Computation Conference (GECCO’04). 2004, p. 105-116.
LI X. Efficient Differential Evolution using Speciation for Multimodal Function Optimization. In Proceedings of 7th Genetic and Evolutionary Computation Conference (GECCO’05). Washington, DC: 2005, p. 873-880.
LI X. Niching Without Niching Parameters: Particle Swarm Optimization using a Ring Topology. IEEE Transactions on Evolutionary Computation, 2010, 14, p. 150-169.
LIN C.Y and WU W. H. Niche Identification Techniques in Multimodal Genetic Search with Sharing Scheme. Advances in Engineering Software, 2002, 33, p. 779-791.
MAHFOUD S. W. Crowding and Preselection Revisited. In Proceedings of the 2nd International Conference on Parallel Problems Solved form Nature. North-Holland, Amsterdam: 1992, p. 27-36.
MENGSHEOL O. and GOLDBERG D. Probabilistic Crowding: Deterministic Crowding with Probabilistic Replacement. In Proceedings of the 1st Genetic and Evolutionary Computation Conference (GECCO’99). 1999, p. 409-416.
MILLER B. L. and SHAW M. J. Genetic Algorithms with Dynamic Niche Sharing for Multimodal Function Optimization. In Proceedings of the IEEE International Conference on Evolutionary Computation. Piscataway, NJ: IEEE Press, 1996, p. 786-791.
NAGATA Y. Niching Method for Combinatorial Optimization Problems and Application to JSP. In Proceedings of the IEEE Congress on Evolutionary Computation. Vancouver, BC, Canada: 2006.
PÉTROWSKI A. A clearing procedure as a niching method for genetic algorithms. In Proceedings of the 3rd IEEE International Conference on Evolutionary Computation. Nagoya, Japan:1996, p. 798-803.
QU B.Y. and SUGANTHAN P. N. Novel Multimodal Problems and Differential Evolution with Ensemble of Restricted Tournament Selection. In Proceedings of the IEEE Congress on Evolutionary Computation. Barcelona, Spain: 2010, p. 3480-3486.
SACCO W. F., MACHADO M. D., PEREIRA C.M. and SCHIRRU R. The fuzzy clearing approach for a niching genetic algorithm applied to a nuclear reactor core design optimization problem. Annals of Nuclear Energy, 2004, 31, p. 55-69.
SARENI B. and KRÄHENBÜHL L. Fitness sharing and niching methods revisited. IEEE Transactions on Evolutionary Computation, 1998, 2(3), p. 97-106.
SHIR O.M. and BÄCK T. Niche radius adaptation in the cma-es niching algorithm. In Proceedings of the 9th International Conference on Parallel Problems Solved form Nature. Reykjavik: 2006, p. 142-151.
SMITH R., FORREST S. and PERELSON A. S. Searching for diverse, cooperative populations with genetic algorithms. Evolutionary Computation, 1993, 1(2), pp. 127-149.
YANG R. Line-breeding Schemes for Combinatorial Optimization. Lectures Notes in Computer Science 1498, Springer- Verlag Berlin, 1998, p. 448-457.
Recibido:22/04/2013
Aceptado:9/06/2013
















