ARTÍCULO DE REVISIÓN

 

Aprendizaje supervisado de funciones de distancia: estado del arte

 

Supervised distance metric learning: state of the art

 

 

Bac Nguyen Cong^1*, Jorge Luis Rivero Pérez², Carlos Morell¹

¹ Universidad Central “Marta Abreu” de las Villas. Carretera Camajuaní, km 5 ½. Santa Clara, Villa Clara, Cuba.
² Universidad de Cienfuegos “Carlos Rafael Rodríguez”. Carretera a Rodas. Km. 4. Cienfuegos, Cuba.

*Autor para la correspondencia: [e-mail]

 

 

---

RESUMEN

La selección de una función de distancia adecuada es fundamental para los algoritmos de aprendizaje basados en instancias. Tal función de distancia dicta el éxito o el fracaso de dichos algoritmos. Recientemente se ha demostrado que, incluso una simple transformación lineal de las características de entrada, puede conducir a mejoras significativas en la clasificación de los algoritmos como k vecinos más cercanos (k-NN). Una de las principales aplicaciones de estos algoritmos es su hibridación con algoritmos de aprendizaje basados en instancias, aprendiendo así una función de distancia para la aplicación específica y no utilizando una función de distancia general; lo que ha demostrado mejorar los resultados del aprendizaje. El presente artículo presenta una panorámica sobre el aprendizaje de funciones de distancia y su modelado como un problema de optimización. Luego aborda diferentes enfoques de aprendizaje a partir de la disponibilidad de información en forma de restricciones, enfocándose en el supervisado, y bajo este los enfoques globales y locales. Además se describen modelos y estrategias de los algoritmos más representativos de cada enfoque.

Palabras clave: aprendizaje de funciones de distancia, clasificación, k vecinos más cercanos.

---

ABSTRACT

The selection of a suitable distance function is fundamental to the instance-based learning algorithms. Such distance function influences the success or failure of these algorithms. Recently it has been shown that even a simple linear transformation of the input attributes can lead to significant improvements in classification algorithms as k-Nearest Neighbour (k-NN). One of the main applications of these algorithms is in the hybridization with instance-based  learning algorithms and in that sense learning a distance metric for the application at hand and not using a general distance function; which has been shown to improve the learning results. This article presents an overview of distance metric learning, and it is modeled as an optimization problem. It then discusses different approaches to learning from the availability of information in the form of restrictions, focusing on supervised approach, and under it the global and local ones. Further models and strategies of the most representative algorithms of each approach are described.

Key words: classification, distance metric learning, k-Nearest Neighbours.

---

 

 

INTRODUCCIÓN

Uno de los métodos clásicos y más simples para clasificación basado en instancias es el de los k vecinos más cercanos, del inglés k-Nearest Neighbour (k-NN) (Cover and Hart, 1967). La regla de k-NN clasifica cada instancia según la clase mayoritaria entre los vecinos más cercanos que se encuentran en el conjunto de entrenamiento utilizando una función de distancia o similitud. Por la propia naturaleza de su regla de decisión, la calidad de la clasificación del método depende de la manera en que se calculan las distancias entre las diferentes instancias. Cuando no hay ningún conocimiento previo disponible, o incluso cuando hay conocimiento previo, la mayoría de las implementaciones de k-NN utilizan la función de distancia Euclidiana (suponiendo que las instancias se representan como vectores de entrada). La selección de una función de distancia adecuada es fundamental para un buen comportamiento de cualquiera de los algoritmos de clasificación basados en instancias, tales como k-Means (Hartigan and Wong, 1979), el prototipo más cercano (Hastie, et al. 2009), y otros. Las funciones de distancia como la Euclidiana ignoran cualquier regularidad estadística que existe entre los atributos de las instancias del conjunto de entrenamiento (Bellet, et al. 2013; Kulis, 2012). Se puede adaptar la función de distancia en diversos campos como, clasificación (Davis, et al. 2007; Fu 2014; Luo, et al. 2015; Weinberger and Saul, 2009), visión por computadora (Fu, 2014; Guillaumin, et al. 2009; Hirzer, et al. 2012; Koestinger, et al. 2012), recuperación de información (Lee, et al. 2008; McFee and Lanckriet ,2010; Schultz and Joachims, 2004) o bioinformática (Kato and Nagano, 2010; Wang, et al. 2012a), según el problema que se quiere resolver. Por ejemplo, si se quisieran clasificar imágenes de rostros según su edad y según su género no sería óptimo utilizar la misma función de distancia para estos dos problemas, incluso si en ambas tareas, las distancias se calculan entre el mismo conjunto de características extraídas (por ejemplo, los píxeles, histogramas de color) (Kulis, 2012). Motivados por estas cuestiones, un número de investigadores han demostrado que se puede mejorar la efectividad de la clasificación del algoritmo k-NN mediante el aprendizaje de funciones de distancia a partir de un conjunto de entrenamiento (Friedman, 1994; Goldberger, et al. 2004; Martin, et al. 2012; Wang, et al. 2012b; Weinberger, et al. 2006; Weinberger, and Saul 2009; Xing, et al. 2003; Zhang, et al. 2003). Estos métodos funcionan mediante la explotación de información sobre las distancias entre las instancias que está intrínsecamente disponibles en las instancias de entrenamiento. Por ejemplo, en el problema de recuperación de información, restricciones del tipo “el documento q  es más similar al documento a  que al documento p” pueden ser escogidas mediante retroalimentación a partir del comportamiento del usuario. Estas restricciones contienen información importante para adaptar la función de distancia. En los casos supervisados, las restricciones se pueden inferir a partir de las instancias de entrenamiento partiendo del principio de que “la distancia entre instancias de la misma clase debe ser más pequeña que la distancia entre instancias de clases diferentes”.

En este trabajo, se abordan los aspectos generales del aprendizaje de funciones de distancia (en inglés Distance Metric Learning), específicamente el enfoque supervisado de aprendizaje, así como una revisión de algunos de los algoritmos más representativos para evaluar su aplicabilidad a problemas de clasificación basados en instancias.

 

DESARROLLO

En esencia, el objetivo del aprendizaje supervisado de funciones de distancia es aprender una función (métrica) de distancia, generalmente la distancia de Mahalanobis , entre dos instancias , y sus clases correspondientes  para una aplicación específica, usando para ello información del conjunto de entrenamiento. Para esto la mayoría de los algoritmos que aprenden una función de distancia tratan de resolver un problema de optimización con restricciones, cuyo modelo tiene la forma siguiente (Bellet, Habrard and Sebban 2013):

,

donde R  es un regularizador sobre el parámetro M, la función l_i(M, R_i) es la función costo que penaliza la violación de las restricciones R_i  y  es el parámetro de regularización. Mientras que las formulaciones son diferentes para cada modelo, las restricciones son uno de los dos tipos siguientes:

• Restricciones por pares:

S = {(X_i, X_j): x_i y x_j deben ser similares}

D = {(X_i, X_j): x_i y x_j deben ser disimilares}

•  Restricciones relativas:

T = {(X_i, X_j, X_k): x_i debe estar más cercano al x_{j que a} x_k}

Se trata de encontrar la matriz M que sea simétrica semidefinida positiva para garantizar que D_M (x_i y x_j) sea una métrica válida. Luego la matriz M  resultante se puede utilizar para mejorar el rendimiento de los algoritmos basados en instancias. Es necesario acotar que la distancia de Mahalanobis se puede considerar como una generalización de la distancia Euclidiana (ver figura 1). En particular, las distancias Euclidianas se recuperan haciendo que M  sea igual a la matriz identidad.

En la bibliografía suelen utilizarse los términos función, métrica y seudométrica, de ahí que a continuación se presentan algunos términos básicos y propiedades las cuales, de cumplirse, definen al término en cuestión.

Definición 1 (Métrica) La aplicación  sobre un espacio X  se denomina una métrica si  se satisfacen las propiedades (Bellet, Habrard and Sebban, 2013):

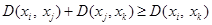1.  (desigualdad triangular).
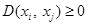2.  (no negatividad).
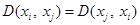3.  (simetría).
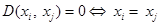4.  (distinguibilidad).

En un sentido estricto, una función que satisface las tres primeras propiedades pero no la cuarta, se denomina seudométrica. Visto esto se puede obtener una familia de métricas sobre el espacio X  calculando la distancia Euclidiana después de aplicar una transformación lineal L sobre las instancias de entrada x´ = Lx. Esta métrica calcula la distancia cuadrada sobre los datos transformados por L  (Bellet, Habrard and Sebban, 2013; Kulis, 2012):

La transformación lineal en la ecuación está parametrizada por la matriz L. Está demostrado que la ecuación (1) define una métrica válida si L  es una matriz de rango completo. La distancia cuadrada se puede expresar en el término de la matriz M=L^TL. Cualquier matriz M  formada por esta vía, se garantiza que es semidefinida positiva, es decir, no tiene valores propios negativos. Entonces, la distancia pudiera calcularse de la siguiente manera:

Coincidiendo con la distancia de Mahalanobis:

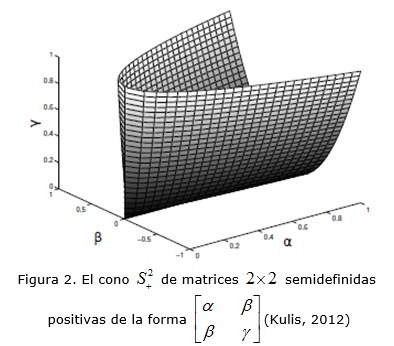
Originalmente, este término era utilizado para describir las formas cuadráticas en distribuciones gaussianas (Mahalanobis, 1936), donde la matriz M desempeñó el papel de la matriz de covarianza inversa. Aquí se usa , donde  es el cono de las matrices simétricas semidefinidas positivas d x d  de valores reales (ver la figura 2). Entonces, la distancia de Mahalanobis se puede parametrizar en función de la matriz L  o de la matriz M   aumentando así las posibilidades de modelación. Se debe tener en cuenta que la matriz L define de forma única a la matriz M, mientras que la matriz M define L hasta la rotación, es decir, que no afecta el cálculo de las distancias. Esta equivalencia sugiere dos enfoques diferentes de aprendizaje de funciones de distancia. En particular, se puede estimar una transformación lineal L  o estimar una matriz positiva semidefinida M. Nótese que en el primer enfoque, la optimización es sin restricciones, mientras que en el segundo enfoque, es importante para hacer cumplir la restricción de que la matriz M sea semidefinida positiva. Por lo general es más complicado resolver un problema de optimización con muchas restricciones, sin embargo, este segundo enfoque tiene ciertas ventajas que se exploran en las secciones posteriores. Muchos investigadores han propuesto formas de estimar la distancia de Mahalanobis con el propósito de calcular distancias en la clasificación k-NN (Bar-Hillel, et al. 2003; Chen and Sun, 2010; Hastie and Tibshirani, 1996; Semerci and Alpaydın, 2013; Weinberger, Blitzer and Saul, 2006; Weinberger and Saul, 2009). Para la clasificación k-NN, se busca una transformación lineal tal que los vecinos más cercanos calculados a partir de las distancias en la ecuación (2) compartan las mismas etiquetas de clase.

Existen varias categorizaciones para los algoritmos que aprenden una función de distancia (Bellet, Habrard and Sebban, 2013) pero, dependiendo de la disponibilidad de las instancias de entrenamiento, los algoritmos para el aprendizaje de funciones de distancia se pueden dividir en dos categorías: aprendizaje supervisado de funciones de distancia (en inglés supervised distance metric learning) y aprendizaje no supervisado de funciones de distancia (en inglés unsupervised distance metric learning). Este artículo se centra en la categoría de aprendizaje supervisado. A diferencia de la mayoría de los algoritmos de aprendizaje supervisado donde las instancias de entrenamiento son etiquetadas a partir de sus clases, en los algoritmos supervisados de aprendizaje de funciones de distancia, las instancias de entrenamiento se convierten en restricciones por parejas: restricciones de equivalencia, son los pares de instancias que pertenecen a las mismas clases, o sea los que conforman el conjunto S definido anteriormente y restricciones no equivalentes que son los pares de instancias que pertenecen a diferentes clases, definidos en el conjunto D. Otra dimensión que sirve para caracterizar el aprendizaje supervisado de funciones de distancia es el alcance de las restricciones. Si las restricciones se forman en la vecindad de cada ejemplo de aprendizaje entonces se denomina local, en otro caso se denomina global. A continuación, en las siguientes secciones, se detallan algunos aspectos del aprendizaje supervisado de funciones de distancia tanto global como local.

 

RESULTADOS Y DISCUSIÓN

Aprendizaje supervisado global de funciones de distancia.

Los algoritmos bajo esta categoría aprenden una función de distancia que garantiza la cercanía de todas las instancias de datos de la misma clase y que separa todas las instancias de datos de diferentes clases (Bar-Hillel, et al. 2005; Davis, Kulis, Sra and Dhillon, 2007; Fisher, 1936; Globerson and Roweis, 2005; Jolliffe, 2005; Koestinger, Hirzer, Wohlhart, Roth and Bischof, 2012; Shental, et al. 2002; Xing, Ng, Jordan and Russell, 2003). El método más representativo de esta categoría es el propuesto por (Xing, Ng, Jordan and Russell, 2003), que formula el aprendizaje de funciones de distancia como un problema de programación convexa restringida (en inglés constrained convex programming). Este método aprende una función de distancia globalmente que minimiza la distancia entre los pares que forman las restricciones de equivalencia sujetos a la restricción de que los pares no equivalentes están bien separados. A continuación se abordan especificidades de las restricciones por pares. Luego, se hace un estudio de los modelos de aprendizaje supervisado global de funciones de distancia propuestos en (Xing, Ng, Jordan and Russell, 2003) y (Davis, Kulis, Sra and Dhillon, 2007). Por último, se presentará un modelo probabilístico de aprendizaje de funciones de distancia.

Restricciones por pares

Como se ha abordado anteriormente, y a diferencia del aprendizaje supervisado típico donde cada instancia de entrenamiento se anota con su etiqueta de clase, la información de la clase en el aprendizaje de funciones de distancia se especifica generalmente en forma de restricciones por pares: (1) las restricciones de equivalencia, que establecen que los elementos de un par determinado son similares y deben estar cerca en el espacio métrico inducido por la función de distancia aprendida, y (2) las restricciones no equivalentes, que indican que dos instancias determinadas son diferentes y por tanto no deben estar cercanos en tal espacio. La mayor parte de los algoritmos de aprendizaje tratan de encontrar una función de distancia que mantiene juntos a todos los pares que forman parte de las restricciones de equivalencia, mientras que separa las instancias que forman parte de las restricciones no equivalentes. En (Domeniconi and Gunopulos, 2001), proponen un algoritmo que ajusta los pesos de los rasgos adaptativamente para cada instancia de prueba, reflejando así la importancia de las características en la determinación de la etiqueta de la clase de las instancias de prueba. En (Friedman, 1994), la función de distancia también se modifica en dependencia de la región donde se localiza la instancia a clasificar. En (Bar-Hillel, Hertz, Shental and Weinshall, 2003; Xing, Ng, Jordan and Russell, 2003), la función de distancia es explícitamente aprendida para reducir al mínimo la distancia entre instancias de datos dentro de las restricciones equivalentes y maximizar la distancia entre instancias de datos en las restricciones no equivalentes.

Aprendizaje supervisado global de funciones de distancia por programación convexa

Por lo general, y dadas las restricciones de equivalencia en S y las de no equivalencia en D esta categoría conduce a problemas de programación convexa, como en  (Xing, Ng, Jordan and Russell, 2003):
                                                
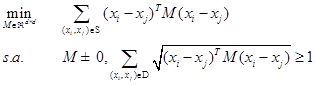
Debe tenerse en cuenta que la restricción como un problema semidefinido positivo  es necesaria para garantizar las propiedades de no negatividad y de desigualdad triangular entre dos instancias de datos. Aunque el problema cae en la categoría de programación convexa, no puede ser resuelto de manera eficiente debido a que no puede ser modelado como un problema de programación cuadrática ni programación semidefinida. En primer lugar, no cae en ninguna clase especial de programación de convexa, tales como la programación cuadrática (Gill, et al. 1981) y la programación semidefinida (Vandenberghe and Boyd, 1996). Como resultado, sólo puede ser resuelto por el enfoque genérico, que es incapaz para tomar ventaja de las características especiales del problema. En segundo lugar, como se señaló en (Zhang, Kwok and Yeung, 2003), el número de parámetros es casi cuadrático con respecto al número de rasgos. Esta propiedad es difícil de escalar a un gran número de rasgos. Otra desventaja es que es incapaz de estimar la probabilidad de que cualquiera de las instancias de datos comparta la misma clase (Bellet and Habrard, 2012). A continuación se describe un algoritmo representativo de este enfoque.

Information Theoretic Metric Learning (ITML)

En (Davis, Kulis, Sra and Dhillon, 2007) adoptaron un enfoque de teoría de la información para optimizar la matriz M bajo una amplia gama de posibles restricciones y el conocimiento previo de la distancia de Mahalanobis. Esto se realiza mediante la regularización de la matriz M tal que sea lo más cercana posible de una matriz M₀ conocida previamente. Esta cercanía se interpreta como una divergencia Kullback-Leibler (KL) entre las dos matrices gaussianas correspondientes a M y M₀ respectivamente. Típicamente, las otras restricciones son de la forma  para los pares positivos y  para los pares negativos. El equilibrio entre la satisfacción de las restricciones y la regularización se controla en la función objetivo utilizando un parámetro adicional Y. Los parámetros M₀, restricción superior u, restricción inferior l tienen que ser proporcionados:
                                             
La distancia KL proporciona una medida fundada de cercanía entre dos funciones de distancia de Mahalanobis y constituye la base problémica del modelo. Teniendo en cuenta las parejas de instancias similares S y parejas de diferentes clases D, el problema de aprendizaje de funciones de distancia resulta en:
                                                    

Se demostró en (Davis, Kulis, Sra and Dhillon, 2007) que la función objetivo se puede expresar como un tipo particular de la función Divergencia Bregman, que se permite adaptar al método de Bregman (Censor, 1997) para resolver el aprendizaje de funciones de distancia. También, se muestra una similitud con un problema propuesto del tipo low-rank kernel learning (Kulis, et al. 2006), lo que permite la kernelización del algoritmo.
                                         

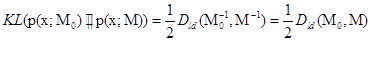
Donde las matrices M y M₀ son de tamaño d x d  y:

 

Se puede aprovechar la equivalencia para expresar el problema de aprendizaje de distancia de la siguiente manera:     
   
                                    

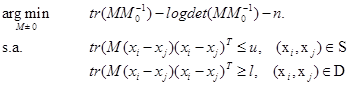
La optimización se basa en la proyección Bregman, que proyecta la solución actual en una única restricción a través de la regla de actualización:

                                                                    
Una limitación de ITML es que la selección de la matriz M₀ puede tener una influencia importante en la calidad de la función de distancia M.

Enfoque probabilístico para aprendizaje de funciones de distancia global

Dada la complejidad de cálculo del problema de optimización originalmente descrito en (Xing, Ng, Jordan and Russell, 2003; Ying and Li, 2012), para simplificar el cálculo, un método probabilístico de aprendizaje de funciones de distancia global puede ser establecido sobre la base de la fórmula. Siguiendo la idea de (Friedman, 1994), se asume un modelo de regresión logística en la estimación de la probabilidad de que cualquiera de las dos instancias de datos x_i y x_j compartan la misma clase, es decir:

                                                  

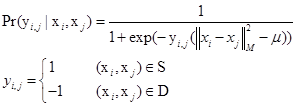
El parámetro u  representa el umbral y dos puntos de datos x_i y x_j tendrán la misma etiqueta de clase sólo cuando su distancia  sea menor que el umbral u. Entonces el logaritmo total de verosimilitud tanto de las restricciones equivalentes S como de las restricciones no equivalentes D se expresa como:
                                                           
Usando la estimación de máxima verosimilitud, se puede plantear el problema de aprendizaje de funciones de distancia en el siguiente problema de optimización:

La dificultad con la solución de la fórmula (3) se encuentra en la restricción  semidefinida positiva. Para simplificar los cálculos, se modela la matriz M, utilizando el espacio propio de instancias. Sea T = (x₁, x₂,...,x_n) el conjunto de vectores que incluye todas las instancias de conjuntos de entrenamiento usadas por las restricciones en S y D; luego, sea   los pares de la correlación entre dos rasgos cualesquiera y sean  los mejores K () vectores propios de la matriz M, siendo M  una combinación lineal de los K vectores propios:

Donde (Y₁,...Y_K) son los pesos no negativos para la combinación lineal, entonces usando la forma paramétrica (4), la ecuación (3) se escribe como:

                                

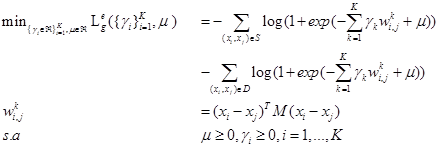
El problema de optimización anteriormente descrito es un problema de programación convexa que puede ser resuelto aplicando el método de Newton. Además, el método anterior permite el aprendizaje no supervisado. Esto es debido que la matriz M  puede ser construida utilizando tanto los datos etiquetados como los no etiquetados.

Aprendizaje supervisado local de funciones de distancia

Según (Hastie and Tibshirani, 1996) y (Friedman, 1994), el método k-NN depende de que las probabilidades condicionales de la clase del vecino más cercano local sean constantes. Este supuesto podrá atenuarse si se asume que la probabilidad condicional en la vecindad de instancias de prueba es suave o una función de cambio lento. Sin embargo, este supuesto no es necesariamente cierto, ya que por ejemplo, para el área cerca de la frontera de decisión entre las dos clases, se espera que las etiquetas de clase cambien drásticamente. En otras palabras, el objetivo de la adaptación de aprendizaje es obtener una vecindad de una instancia de prueba dado con una alta consistencia en la asignación de etiquetas de clase. Además de los algoritmos para el aprendizaje de funciones de distancia, varios artículos (Domeniconi and Gunopulos, 2001; Friedman, 1994; Zhang, Kwok and Yeung, 2003) presentan enfoques para aprender las funciones durante la etapa de clasificación. Este enfoque permite mejorar los resultados del algoritmo k-NN. En específico, estos enfoques modifican los pesos de rasgos basados en las instancias de prueba. Estos enfoques se conocen como algoritmos de aprendizaje adaptables. A continuación se presentan algunos algoritmos representativos de este enfoque (Yang and Jin, 2006).

Local Linear Discriminative Analysis
Este clasificador hace una transformación lineal del espacio de representación de los atributos y para ello encuentra los vectores propios de la matriz  . Aquí S_W denota la covarianza entre las clases, y S_b denota la covarianza inter-clase. La matriz  captura  la densidad de cada clase, y la matriz S_b representa la separación de la clase. Así, los vectores propios principales de T mantendrán las instancias de datos de la misma clase cerca y las instancias de datos de diferentes clases separados. Luego se forma una matriz de transformación S_T apilando los vectores propios de T junto a los rasgos discriminatorios y  se calcula como Y= S_WX, donde X es la entrada de instancias de prueba.
Basado en el método Linear Discriminant Analysis (LDA) (Fisher, 1936), (Hastie and Tibshirani, 1996) propone localizar tanto S_b como S_W a través de un procedimiento iterativo: inicializa la función de distancia como una matriz idéntica, es decir, se parte de una distancia Euclidiana. En el primer paso, se calcula S_b y S_W utilizando los puntos que se encuentran en las cercanías del punto de prueba X₀ medido por la . En el segundo paso, los estimados de S_b y S_W se utilizan para actualizar  de la siguiente manera:

                                                              

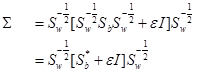
Neighborhood Components Analysis (NCA)

El algoritmo Neighborhood Components Analysis (NCA) propuesto en (Goldberger, Roweis, Hinton and Salakhutdinov, 2004) aprende una distancia de Mahalanobis para el clasificador k-NN maximizando la validación cruzada leave-one-out. A continuación se presenta la esencia del algoritmo.
El conjunto de datos etiquetados se denota por . Para garantizar que la matriz de distancia aprendida sea simétrica y semidefinida positiva (Goldberger, Roweis, Hinton and Salakhutdinov, 2004) asume que M tiene la forma M= L^TL donde L puede ser cualquier matriz. Esta forma paramétrica garantiza que la distancia entre dos instancias de datos u e v será positiva, dado el hecho de que                   

                           

Dado una instancia x_i, un vecino soft de x_i se define por P_ij, que es la probabilidad para seleccionar x_j como el vecino de x_i, que comparte la misma etiqueta de clase con x_i. La probabilidad P_ij se define como:
                                                                 
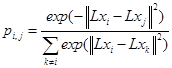
El conjunto de instancias que comparten la misma clase con x_i se denota por . Entonces, la  probabilidad de clasificar correctamente x_i se expresa , y el número esperado de puntos clasificados correctamente es . Tomando la derivada de  con respecto a primer orden, se obtiene:
                                    
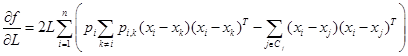
En lugar de utilizar la exactitud promedio de clasificación, (Goldberger, Roweis, Hinton and Salakhutdinov, 2004) sugiere el uso de la validación cruzada dejando uno fuera de la función objetivo , es decir:
                                                                    
NCA tiene los siguientes inconvenientes:

• NCA sufre del problema de escalabilidad ya que su función objetivo se diferencia de la matriz de distancia y el número de parámetros en L tiene una dependencia cuadrática del número de atributos. Por lo tanto, la actualización de la matriz de distancia alcanzará una dimensión intratable para problemas medianos.
• El algoritmo de ascenso del gradiente propuesto por NCA no garantiza la convergencia a máximos locales.
• NCA tiende a sobre-aprendizaje de los datos de entrenamiento si el número de instancias de entrenamiento es insuficiente. Esto ocurre a menudo cuando las instancias de datos están representadas en el espacio de alta dimensión.

Large Margin Nearest Neighbour Metrics (LMNN)

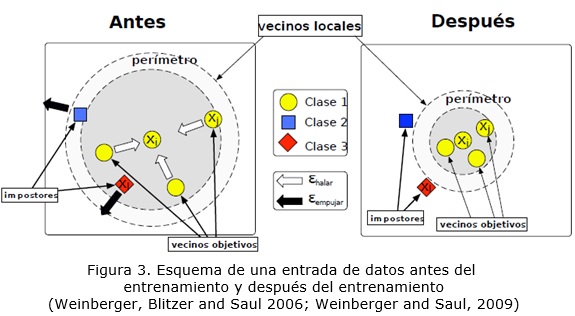
En  (Weinberger, Blitzer and Saul 2006; Weinberger and Saul, 2009) introdujeron un método que aprende una matriz de distancia M para mejorar los resultados de k-NN conocido por LMNN. La intuición es que para cada instancia la función de distancia debe hacer que sus k vecinos más cercanos de la misma clase ---vecinos objetivos--- estén más cerca entre sí que las instancias de clases diferentes. La función objetivo se compone de dos términos: el primer término minimiza las distancias entre los vecinos objetivos, mientras que el segundo término es una función de pérdida que penaliza la existencia de instancias de clases diferentes en la vecindad definida por los vecinos objetivos más un margen fijo. En lugar de usar las restricciones por pares, como en los casos anteriores, este algoritmo aprende a partir de  restricciones relativas (i,j,l). La métrica aprendida M tiene que cumplir que la distancia entre los vecinos x_i y x_j debe ser menor que la distancia entre x_i y x_i. Según las definiciones anteriores x_j sería un vecino objetivo y x_i un impostor, siempre relativo a la instancia x_i. Este tipo de restricciones permite tener en cuenta el comportamiento local del algoritmo de los vecinos más cercanos, realizándose a través de la siguiente función objetivo:
                                                  
El primer término de la ecuación minimiza la distancia entre los vecinos objetivos x_i, x_j, indicado por . El segundo término denota la cantidad de impostores que invaden el perímetro de i y j. Un impostor l  es una entrada de diferentes clases (Y_il=0) que tiene una variable de holgura positiva :
                                                          
En la figura 3 se ilustra la idea de la clasificación de LMNN. Antes del aprendizaje, una instancia cualquiera tiene tantos vecinos objetivos como impostores en su vecindad. Durante el aprendizaje, los impostores son empujados fuera del perímetro establecido por los vecinos objetivos. Después de aprender, se crea un margen finito entre el perímetro y los impostores. La figura 3 muestra la idea donde los errores de clasificación de k-NN en el espacio original son corregidos por el aprendizaje de una transformación lineal apropiada.

La función de pérdida es una función convexa de los elementos en la matriz M. En particular, el primer término de la función de pérdida (penalizando a las grandes distancias entre los vecinos objetivos) es lineal en los elementos de M, mientras que el segundo término (que penaliza a los impostores) se deriva de la pérdida de articulación convexa. Para formular la optimización de la ecuación de pérdida se puede utilizar un programa semidefinido (SDP por sus siglas en inglés: Semidefinite Program), sin embargo, para resolverla, hay que convertirla en una forma más estándar.
Un SDP se obtiene mediante la introducción de variables de holgura que imitan el efecto de la pérdida. En particular, se introducen las variables no negativas de holgura  para todas las ternas de vecinos objetivos  y los impostores x_l. La variable holgura  se utiliza para medir el margen en que se viola la desigualdad en la ecuación de pérdida. Se introducen las variables de holgura para controlar estas violaciones de margen y obtener el SDP:

                                    

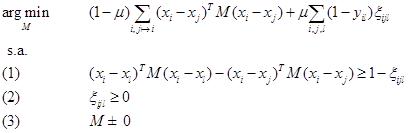
Mientras que los SDP en esta forma pueden ser resueltos por los paquetes de software estadísticos estándares, los solucionadores de propósito general tienden a decrecer notablemente la calidad de los resultados en cuanto aumenta el número de restricciones. Para este algoritmo, se implementó un método propio especial, aprovechando el hecho de que la mayoría de las variables de holgura  nunca alcanzan valores positivos. Las variables de holgura   son dispersas porque la mayoría de las entradas x_i y x_l están bien separadas con respecto a la distancia entre x_i y cualquiera de sus vecinos objetivos x_j. Estos resultan en muy pocas restricciones activas en el SDP, por lo tanto, se puede lograr un gran aumento de velocidad de procesamiento mediante la resolución de un SDP que sólo supervisa una fracción de las restricciones de margen. Luego se utiliza la solución resultante como punto de partida para el SDP.

 

CONCLUSIONES

El desarrollo de métodos para el aprendizaje de funciones de distancia a partir de los datos ha tenido un desarrollo imponente en los últimos años. En su mayoría los enfoques se caracterizan por formular un problema de optimización a partir de restricciones que se obtienen de las instancias de aprendizaje. El proceso de minimización o maximización de la función objetivo que codifica las restricciones se realiza mediante un costoso algoritmo iterativo. Estos métodos, cuando se utilizan de conjunto con un clasificador vago como el k-NN, permiten incrementar la calidad de la clasificación al costo de una complejidad computacional alta. En el estudio realizado se abordaron aspectos generales del aprendizaje de funciones de distancia así como su aplicabilidad a la mejora de algoritmos de clasificación basados en instancias. Dentro del enfoque supervisado se distinguieron dos categorías que dependen de la forma en que se obtienen las restricciones, esto es, en la vecindad de cada instancia (local) o en todo el espacio de representación (global). En cada categoría se detallaron las ideas detrás de las implementaciones de los algoritmos más representativos. Este trabajo resulta de utilidad para comprender la esencia del aprendizaje de funciones de distancia y facilita la selección de que algoritmos aplicar dada la disponibilidad de información en forma de restricciones. 

 

REFERENCIAS BIBLIOGRÁFICAS

BAR-HILLEL, A., T. HERTZ, N. SHENTAL AND D. WEINSHALL. Learning distance functions using equivalence relations. In ICML. 2003, vol. 3, p. 11-18.

BAR-HILLEL, A., T. HERTZ, N. SHENTAL AND D. WEINSHALL Learning a mahalanobis metric from equivalence constraints. Journal of Machine Learning Research,  2005, 6(6), 937-965.

BELLET, A. AND A. HABRARD Robustness and Generalization for Metric Learning. arXiv preprint arXiv:1209.1086,  2012.

BELLET, A., A. HABRARD AND M. SEBBAN A survey on metric learning for feature vectors and structured data. arXiv preprint arXiv:1306.6709,  2013.

CENSOR, Y. Parallel optimization: Theory, algorithms, and applications. Edtion ed.: Oxford University Press, 1997.

CHEN, Q. AND S. SUN. Hierarchical large margin nearest neighbor classification. In Pattern Recognition (ICPR), 2010 20th International Conference on. IEEE, 2010, p. 906-909.

COVER, T. AND P. HART Nearest neighbor pattern classification. Information Theory, IEEE Transactions on,  1967, 13(1), 21-27.

DAVIS, J., B. KULIS, S. SRA AND I. DHILLON. Information-theoretic metric learning. In in NIPS 2006 Workshop on Learning to Compare Examples. 2007.

DOMENICONI, C. AND D. GUNOPULOS. Adaptive nearest neighbor classification using support vector machines. In Advances in Neural Information Processing Systems. 2001, p. 665-672.

FISHER, R. A. The use of multiple measurements in taxonomic problems. Annals of eugenics,  1936, 7(2), 179-188.

FRIEDMAN, J. H. Flexible metric nearest neighbor classification. Unpublished manuscript available by anonymous FTP from playfair. stanford. edu (see pub/friedman/README),  1994.

FU, Y. Multi-view Metric Learning for Multi-view Video Summarization. arXiv preprint arXiv:1405.6434,  2014.

GILL, P. E., W. MURRAY AND M. H. WRIGHT Practical optimization  1981.

GLOBERSON, A. AND S. T. ROWEIS. Metric learning by collapsing classes. In Advances in neural information processing systems. 2005, p. 451-458.

GOLDBERGER, J., S. ROWEIS, G. HINTON AND R. SALAKHUTDINOV. Neighbourhood components analysis. In Advances in Neural Information Processing Systems 17. MIT Press, 2004, p. 513-520.

GUILLAUMIN, M., J. VERBEEK AND C. SCHMID. Is that you? Metric learning approaches for face identification. In Computer Vision, 2009 IEEE 12th International Conference on. IEEE, 2009, p. 498-505.

HARTIGAN, J. A. AND M. A. WONG A K-Means Clustering Algorithm. Applied Statistics,  1979, 28, 100-108.

HASTIE, T. AND R. TIBSHIRANI Discriminant adaptive nearest neighbor classification. Pattern Analysis and Machine Intelligence, IEEE Transactions on,  1996, 18(6), 607-616.

HASTIE, T., R. TIBSHIRANI, J. FRIEDMAN, T. HASTIE, et al. The elements of statistical learning. Edtion ed.: Springer, 2009.

HIRZER, M., P. M. ROTH, M. KÖSTINGER AND H. BISCHOF. Relaxed pairwise learned metric for person re-identification. In Computer Vision–ECCV 2012. Springer, 2012, p. 780-793.

JOLLIFFE, I. Principal component analysis. Edtion ed.: Wiley Online Library, 2005. ISBN 0470013192.

KATO, T. AND N. NAGANO Metric learning for enzyme active-site search. Bioinformatics,  2010, 26(21), 2698-2704.

KOESTINGER, M., M. HIRZER, P. WOHLHART, P. M. ROTH, et al. Large Scale Metric Learning from Equivalence Constraints. In Proc. IEEE Conf. on Computer Vision and Pattern Recognition. 2012.

KULIS, B. Metric learning: A survey. Foundations & Trends in Machine Learning,  2012, 5(4), 287-364.

KULIS, B., M. A. SUSTIK, TY\'A,S AND I. DHILLON. Learning low-rank kernel matrices. In Proceedings of the 23rd international conference on Machine learning. 2006, p. 505-512.

LEE, J.-E., R. JIN AND A. K. JAIN. Rank-based distance metric learning: An application to image retrieval. In Computer Vision and Pattern Recognition, 2008. CVPR 2008. IEEE Conference on. IEEE, 2008, p. 1-8.

LUO, C., M. LI, H. ZHANG, F. WANG, et al. Metric Learning with Relative Distance Constraints: A Modified SVM Approach. In Intelligent Computation in Big Data Era. Springer, 2015, p. 242-249.

MAHALANOBIS, P. C. On the generalized distance in statistics. Proceedings of the National Institute of Sciences (Calcutta),  1936, 2, 49-55.

MARTIN, M., M. HIRZER, P. WOHLHART, P. M. ROTH, et al. Large scale metric learning from equivalence constraints. In CVPR. IEEE, 2012, p. 2288-2295.

MCFEE, B. AND G. R. LANCKRIET. Metric learning to rank. In Proceedings of the 27th International Conference on Machine Learning (ICML-10). 2010, p. 775-782.

SCHULTZ, M. AND T. JOACHIMS Learning a distance metric from relative comparisons. Advances in neural information processing systems (NIPS),  2004, 41.

SEMERCI, M. AND E. ALPAYDıN. Mixtures of Large Margin Nearest Neighbor Classifiers. In Machine Learning and Knowledge Discovery in Databases. Springer, 2013, p. 675-688.

SHENTAL, N., T. HERTZ, D. WEINSHALL AND M. PAVEL. Adjustment learning and relevant component analysis. In Computer Vision—ECCV 2002. Springer, 2002, p. 776-790.

VANDENBERGHE, L. AND S. BOYD Semidefinite programming. SIAM review,  1996, 38(1), 49-95.

WANG, J., X. GAO, Q. WANG AND Y. LI ProDis-ContSHC: learning protein dissimilarity measures and hierarchical context coherently for protein-protein comparison in protein database retrieval. BMC bioinformatics,  2012a, 13(Suppl 7), S2.

WANG, J., A. WOZNICA AND A. KALOUSIS. Learning neighborhoods for metric learning. In Machine Learning and Knowledge Discovery in Databases. Springer, 2012b, p. 223-236.

WEINBERGER, K., J. BLITZER AND L. SAUL Distance metric learning for large margin nearest neighbor classification. Advances in neural information processing systems,  2006, 18, 1473.

WEINBERGER, K. Q. AND L. K. SAUL Distance metric learning for large margin nearest neighbor classification. The Journal of Machine Learning Research,  2009, 10, 207-244.

XING, E. P., A. Y. NG, M. I. JORDAN AND S. RUSSELL. Distance Metric Learning, With Application To Clustering With Side-Information. In ADVANCES IN NEURAL INFORMATION PROCESSING SYSTEMS 15. MIT Press, 2003, p. 505-512.

YANG, L. AND R. JIN Distance metric learning: A comprehensive survey. Michigan State Universiy,  2006, 2.

YING, Y. AND P. LI Distance metric learning with eigenvalue optimization. The Journal of Machine Learning Research,  2012, 13(1), 1-26.

ZHANG, Z., J. T. KWOK AND D.-Y. YEUNG. Parametric distance metric learning with label information. In IJCAI. 2003, p. 1450.

 

 

Recibido: 09/02/2015
Aceptado: 02/03/2015