ARTÍCULO ORIGINAL

 

Connected Permutations of Vertices for Canonical Form Detection in Graph Mining

 

Permutaciones conexas de vértices para la detección de formas canónicas en la minería de grafos

 

 

Andrés Gago-Alonso^1*

¹ Centro de Aplicaciones de Tecnologías Avanzadas. La Habana, Cuba.

* Autor para correspondencia: [e-mail]

 

 

---

ABSTRACT

Checking redundancies is one of the most significant tasks in graph mining. Canonical forms of graphs are widely used to guarantee and speed up this kind of task. In general, canonical form calculation requires to orderly check partial or complete prefixes of vertex permutations for picking up the codification to unambiguously represent a graph. In this paper, novel theoretical results are introduced for reducing the number of candidate prefixes to a specific subset associated with connected permutations. Furthermore, several interesting mathematical properties are also described and proved, including strong linkages among graph mining, discrete mathematics, and different kinds of canonical forms. Although this paper does not declare a scheme for directly reducing the complexity of finding canonical descriptions, our contributions can open novel opportunities for future improvements in graph mining by interrelating concepts from different existing approaches.

Key words: canonical form, graph isomorphism, connected permutation, adjacency matrix, spanning tree.

---

RESUMEN

La verificación de redundancias es una de las taras más influyentes en la minería de grafos. Las formas canónicas son ampliamente usadas para garantizar y acelerar este tipo de tarea. En general, el cómputo de una forma canónica requiere la verificación parcial o completa de todos los prefijos de permutaciones de vértices, para seleccionar aquellas que representa sin ambigüedad al grafo. En este artículo, se introducen nuevos resultados teóricos enfocados a reducir el número de candidatos prefijos a un subconjunto específico con las permutaciones conexas. Adicionalmente, varias propiedades son también descritas y probadas, incluyendo fuertes vínculos entre minería de grafos, matemática discreta, y diferentes tipos de formas canónicas. Aunque este artículo no declara un esquema para reducir directamente la complejidad computacional para detectar formas canónicas, nuestras contribuciones pueden abrir nuevas oportunidades para obtener futuras mejoras en la minería de grafos, interrelacionando conceptos provenientes de diferentes enfoques que hasta ahora han sido propuestos de manera aislada.

Palabras clave: formas canónicas, isomorfismo de grafos, permutaciones conexas, matriz de adyacencia, árbol de cobertura

---

 

 

INTRODUCTION

Graph mining is gaining more attention and significance, since advances in collecting and storing data have produced an explosive growth in the amount of available structured data (JIANG, 2013; MANSO, 2014; LI, 2015; VO, 2015). This situation has boosted the necessity to develop new algorithms, called graph miners, to transform this big amount of data into useful information for decision makers. The main idea of several graph miners is to grow subgraphs into the graph collection, adding a new edge or perhaps a new vertex at each step, calculating the quality of each grown subgraph, and rejecting those with low scores. Thus, the development of these miners requires techniques for dealing with the redundancy of candidates during mining process, since the same subgraph can be grown in several ways, adding vertices and edges in different orders. This redundancy can significantly increase the execution times in graph mining (GAGO-ALONSO, 2010a; VO, 2015).

One of the most widely used techniques, to avoid redundant search, consists in defining a canonical form of a graph and using it for representing subgraphs during the mining process (BORGELT, 2006). Some kinds of canonical forms have been defined as strings of labels, which are built by concatenating rows or columns of an adjacency matrix of a graph (INOKUCHI, 2000; KURAMOCHI, 2001; HUAN, 2003). Others are defined as codes of tuples, which are obtained from a spanning tree of a graph (YAN, 2002; NIJSSEN, 2004; BORGELT, 2006; LI, 2015, VO, 2015). All of these approaches are focused on calculating the canonical form of a graph, by traversing the set of vertex permutations.

In this paper, novel theoretical results for enacting the significance of a specific subset of vertex permutations, called connected ones, in canonical form calculation tasks are introduced. In fact, a theorem ensuring that only connected permutations need to be checked during these tasks is mathematically proved. In this sense, other propositions characterizing the cardinality of the connected permutation set of specific kind of graphs are presented. These results give distinction to the reduction achieved by this subset regarding the whole set. Thus, a basic framework for future improvements in graph mining is stated. Additionally, a linkage between graph mining and discrete mathematics is described, in one of these new properties.

Additionally, a new kind of code of tuples, called underlying code, is defined. This concept is strongly linked with adjacency matrices and spanning trees, by means of another theorem introduced and proved in this paper. Thus, this linkage opens new research chances in graph mining by mixing the skilled features of the above mentioned kind of canonical forms.
The rest of this paper is organized as follows. Firstly, the necessary background for understanding the proposed work is described, including basic graph definitions, previously reported propositions, and examples of canonical forms for graphs. Next, the novel framework for characterizing canonical forms using vertex connected permutations is presented, including the description of the underlying code and its relationship with other canonical forms. Finally, conclusions and future work are given.

 

METHODOLOGY

In this section, the necessary background (coming from the literature) for understanding the proposed theoretical framework and the rest of the paper is presented. Examples of canonical forms for labeled graphs are also included.

Graph definitions
This paper is focused on labeled simple undirected graphs. The formal definition of this kind of graph is a classical concept in graph theory, labeled graph (HARARY, 1969), and it is also given below.

The universe of labels is defined as a finite subset, , of positive integer numbers, called labels. Thus, 1 and  are the lowest and highest elements in the universe of labels, respectively.

A labeled graph is a 4-tuple, , where V is a set whose elements are called vertices,  is a set whose elements are called edges (undirected edges are implicitly assumed), each edge is a set with exactly two vertices, L  is a set of labels, , and  is a labeling function for assigning labels to vertices and edges. A vertex  such that , for all edge , is an isolated vertex. If for each pair of vertices and  there is  then G  is named as complete graph.

Let  and  be two graphs. It is said that  is a subgraph of  if , , , and the function  is a restriction of  to . In this case, the notation  is used.

A function f  is an isomorphism between  and , if  is a bijective function where  for each vertex  ,  and  for all edge . A subgraph isomorphism from  to  is an isomorphism from  to a subgraph of ; in such case, the notation  is used.

A path in G  is a sequence of vertices  with  for each ; in this case, it is said that  and  are connected. When , it is said that the path P  is a cycle. The graph G  is connected if for all , ,  and  are connected by at least one path. The proposition 1 offers a good characterization, already reported in the literature, for connected graphs.

Proposition 1. For each graph  with , the following statements are mutually equivalent:

1. G is a connected graph.
2. There is a permutation  of the vertices in V, such that for each 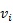, , 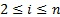there is at least on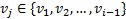e  where .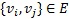

Proof. The proof of theses equivalences can be found in a book of graph theory (DIESTEL, 2000). 

Vertex permutations fulfilling the statement 1 of proposition 1 are called in the scope of this paper as connected permutation. A connected graph without cycles is known as simple tree. The proposition 2 provides relationships, already reported in the literature, among the above mentioned concepts. Moreover, it also supports the most commonly used canonical form definitions.

Proposition 2. For each graph  with , the following statements are mutually equivalent:

1. G is a simple tree.
2. There is a permutation  of the vertices in V, such that for each 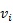, , 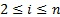there is only one  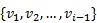where .
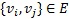3. G is connected with 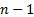 edges.

Proof. The proof of theses equivalences can be found in a book of graph theory (DIESTEL, 2000). 

The graph  is a spanning tree of G if , T  is a simple tree, and . Taking it for granted, let  be a permutation of  according to the statement 2 of proposition 2.

Let us suppose that the vertices u  and v have indices i and j, respectively, according to the permutation P. Let ,  and  be the labels of u, v and , respectively. Without loss of generality, it can be assumed that . The tuple of e  regarding T  is calculated as in (1).

Thus, each edge  can be coded as a tuple, , where . The set  is the vocabulary and it contains the available tuples in the graph G.
Let  and  be two tuple sequences, where  for  and  and  be a total order in . It is said that  according  if one of the following conditions is true

Canonical form based on string of labels

A graph can be represented by its canonical adjacency matrix. This kind of representation has been used in previously reported works for graph mining (INOKUCHI, 2000; KURAMOCHI, 2001; HUAN, 2001; LI, 2015). In this section, the string of labels is defined in a slightly different way regarding previously published works, see (4), giving priority to vertex labels over edge ones.

Let  be a labeled graph with  and let  be a permutation of the vertices in V. The adjacency matrix of G  regarding P  is a lower triangular matrix  where for each :

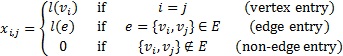
The adjacency matrix is not unique for G. Since each diagonal entry represents a vertex in the graph, each permutation of the set of vertices corresponds to a different adjacency matrix. There are  different adjacency matrices for G.
The string of labels of an adjacency matrix  is built concatenating lower triangular rows of X, see (4). This string is made up by labels in .

Let  be a connected graph and let us suppose that a DFS traversal in G  is performed. A DFS tree  of G is the rooted tree built as follow: the starting vertex in the traversal is the root of T, T is a spanning tree of G () and T contains the edges of G that were used for the DFS traversal ().
The graph G can have many different DFS trees because there is more than one DFS traversal. Each DFS tree T defines a unique order among all the vertices in V. Therefore, each vertex could be numbered according to this DFS order. Thus, a permutation of  according to statement 2 of proposition 2 is given. Assuming , the root of T is numbered with index 1  and the last vertex in the DFS traversal is numbered with index n. The last vertex is also called rightmost vertex of T.
Each edge  is coded as a tuple  according to the DFS tree T, see (1). In addition, a linear order  among the vocabulary  could be defined as follows. Let  and  be two tuples, it is said that  if and only if one of the following statements is true:

• ,
• ,
• ,
• ,
• .

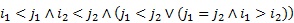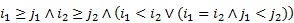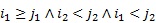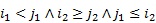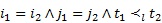The lexicographic order  is used to compare the tuples  and  regarding the last three components in each tuple. This order is determined by comparing the third component as first priority, next the fourth one, and finally the fifth one.
The DFS code of the graph G regarding the DFS tree T is a sequence in  built using . All the tuples obtained from the edges in E are sorted using  to build this sequence. Thus, a graph G can be coded as a sequence of tuples, denoted as , using one of its DFS trees. A canonical form code of a graph G is defined as the minimum tuple sequence according to  among all DFS codes of G.

Other example of ways for building a canonical form codes based on tuples were presented by (BORGELT, 2006), using BFS trees instead of DFS ones, and the proposal of (NIJSSEN, 2004), using graph backbone paths.

 

RESULTS AND DISCUSSION

In this section, results of our research are presented, including the novel framework for characterizing canonical forms using vertex connected permutations, the description of the underlying code and its relationship with other canonical forms.

Novel properties for canonical adjacency matrix

It is a fact that the number of vertex permutation to be checked does not determine the efficiency of canonical form calculations, since the most efficient algorithms, for example (MCKAY, 1981), employ topological properties and label occurrences for pruning partial permutation prefixes. However, there is a worst case where such algorithms require checking the n! Vertex permutations.

An interesting property for describing the set of permutations to be checked is stated in theorem 3. This statement only uses topological properties of graphs for giving distinction to the canonical permutation. Although the cardinality of this set can be irrelevant for graph mining, this property could be used in the future for enriching the already mentioned pruning strategies and speeding up canonical form calculations.

Theorem 3. The canonical permutation of a connected graph is a connected permutation.

Proof. Let us suppose that  is the canonical permutation of a connected graph G and P is non-connected. Thence, there is i, , such that  for all . It is easy to verify that , since G is connected and Vn  cannot be an isolated vertex; thus, . Moreover, there is k, , there is at least one  where , since G is connected.
Let  be the permutation obtained from P by swapping  and . It is easy to prove that . In fact, the substring corresponding to the i-th row ( ) in  is lexicographically lesser than the one in , since this substring in  is , where , whereas in  there is at least a non-zero element on the corresponding substring. Therefore, P cannot be the canonical permutation of G. This fact contradicts the initial assumption. Therefore, the theorem becomes true by reductio ad absurdum.

The following propositions illustrate the number of connected permutations in specifics kind of graphs. Proposition 4 describes the behavior of this number in paths, showing a strong and interesting linkage among graph mining, graph theory, and some special numbers (CONWAY, 1996) coming from discrete mathematics.

Proposition 4. Let  be a graph representing a path; that is, , , and . Then, the number of connected permutations of G.

Proof. Let  be the number of connected permutations of G starting from .

First of all, an interesting function sequence which will be used for counting the number of connected permutations in the graph G is defined. This sequence represents a strong linkage between graph theory and some special numbers.

Let , , be the sequence of functions defined for each , according the following recurrence formula:  for , and  for . In (5), the above mentioned function sequence is shown in expanded way:

where  represents a binomial coefficient or the number of combinations of r  items that can be selected from a set of n  items. Next, the following property of binomial coefficients is underlined:

which can be proved by mathematical induction. For the base case n=1, it is verified that . The inductive step is also achieved since .
After that, it is easy to prove that  using mathematical induction. For the base cases n=1, n=2, n=3, n=4, and n=5, the fact is already known (CONWAY, 1996), and it can be verified in (5). The inductive step is also checked, using (6), since .

Returning to the graph G, it can be seen that there is only one connected permutations starting from , since  must be the second permutation element, and so on. By symmetry, this fact is also true for . For , it can be checked manually that there are n-1  connected permutations starting from ; this fact is also true for -1 by symmetry. Thus, the symmetry , for each , can be proven easily. Besides, it is easy to prove that , for , and it can be calculated, by symmetry, for the remaining vertices. Thus, , for each . Finally, the number of connected permutations of G is , using properties of binomial coefficients.
The Proposition 4 is entirely irrelevant for graph mining, since there are  strategies (NIJSSEN, 2004) for detecting path canonical forms, taking into account the string of labels. Nevertheless, it is presented for illustrating the contrast between connected and non-connected permutation sets in a family of graphs (), without considering labels.
This fact emphasizes the usefulness of theorem 3 for distinguishing the canonical permutation in paths. Similar results can be stated for cycles, see proposition 5.

Proposition 5. Let  be a graph representing a cycle; that is, , , and . Then, the number of connected permutations of G  is .
Proof. For the first position in a permutation, there are n  possibilities. For the subsequent n-2  positions, there are only two possibilities that guarantee a connected permutation. For the last position, there is only one option for the last unselected vertex. Thus, the number of connected permutations of G is .
Until now, analytical formulae for more topologically complex graphs are not given. For example in complete graphs, every permutation is connected. However, even in barely complete graphs, a remarkable number of non-connected permutations (see proposition 6) can be detected.
Proposition 6. Let  be a complete graph with n vertices. The number of connected permutations of G and the number of vertex permutations, n!, are the same. Let  be an edge of G; then, the graph obtained from G by removing e  has  connected permutations.

Proof. The first statement is easy to check since any vertex permutation of G is connected due to completeness. Let us suppose that . Permutations starting with u  and v  are non-connected ones. There are 2(n-2)  permutations in this case. The remaining ones are connected. Therefore, the proof was concluded.
In this way, theorem 3 could be used, in the future, for speeding up algorithms for canonical form calculation. They only need to check connected permutation prefixes, diminishing somehow the number of iterations.

A linkage between Adjacency Matrices and Spanning Trees

The question of establishing connections between adjacency matrices and spanning trees has already been treated. In fact, several variants of constructing a code from an adjacency matrix preserving the equivalence to a spanning tree can be described (BAPAT, 1996). This section contains an example for illustrating the connection with a kind of code only based on tuples describing edges and structurally similar to the already known DFS code.

Let  be a connected graph with n vertices and  be a connected permutation of V. The first edge of , , in P  is defined by us as the edge  such that  and  for all k, . The spanning tree of G, made up by the first edges of any vertex of V  in P, is called by us the underlying spanning tree of G in P.

Let T  be the underlying spanning tree of G in P, coding each edge of G by means of , see (1). Now, a total order in  using P is defined. Let,  and  be two tuples. It is said that  if and only if one of the following statements is true:

• ,
• ,
• ,
• ,
• .
  
  

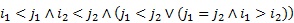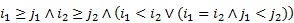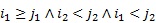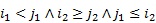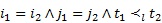The lexicographic order  is used to compare the tuples  and t2  regarding the last three components in each tuple. This order is determined comparing the third component as first priority, next the fifth one, and finally the fourth one.

The underlying code of G given P is defined as a sequence in  constructed using . All of the tuples  obtained from the edges  are sorted using  to build this sequence. Thus, a graph G can be coded asa sequence of tuples, denoted as , using one of its DFS trees. A canonical underlying code of a graph G is defined as the minimum underlying code according to  among all vertex permutations of G.

Underlying code becomes a novel kind of canonical form, preserving a semantics coming from adjacency matrices and showing syntax based on tuples like DFS codes. The following theorem boosts such affirmation.

Theorem 7. Let us suppose that P is the canonical permutation of G. Let  be a graph obtained from G by relabeling vertices and edges, according to , for each  and , where  is the highest element in the universe of labels . The tuple sequence  is the canonical underlying code of .

Proof. Let us suppose that  is a non-canonical underlying code of  and m is the number of edges in G. Thence, there is a permutation  such that , according to . Thus, there is natural number t, , such that , for all k, , and . Let us denote  and .

If t = 1  then . In this case, the string of labels of the matrices  and  starts with the labels of L, where . Therefore, P cannot be the canonical permutation of G. This fact contradicts the initial assumption. Therefore, the theorem becomes true by reductio ad absurdum in this case.

Now, let us assume that , and . Then, it is not difficult to check that the matrices  and  have the same (i - 1)-main minor, and the first difference between them takes place at the i-th row.

Taking into account the definition of , five cases where  are given. Each one of these cases will be individually analyzed.

The first subcase of the first case, ,  and , never takes place in connected permutations of the same graph. In fact, the tuple of the first edge of  in P is always located between  and .

Let us suppose the first case, but in the second subcase , ,  and . In this case,  and the i-th row of  has a non-zero element in a position lesser than the one the i-th row of . Therefore, P can not be the canonical permutation of . This fact contradicts the initial assumption. Therefore, the theorem becomes true by reductio ad absurdum in this case.

Now, let us assume that , and . Then, it is not difficult to check that the matrices  and  have the same (i - 1)-main minor, and the first difference between them takes place at the i-th row.

Taking into account the definition of , five cases where  are given. Each one of these cases will be individually analyzed.

The first subcase of the first case, ,  and , never takes place in connected permutations of the same graph. In fact, the tuple of the first edge of  in P is always located between  and .

Let us suppose the first case, but in the second subcase , ,  and . In this case,  and the i-th row of  has a non-zero element in a position lesser than the one the i-th row of . Therefore, P can not be the canonical permutation of G. This fact contradicts the initial assumption. Therefore, the theorem becomes true by reductio ad absurdum in this case.

The fourth case, , , and , never takes place in connected permutations of the same graph. In fact, the tuple of the first edge of  in P is always located between  and .

In the last case, , , and , the matrices  and  have the first difference between them at the same cell position. In addition, it is verified that , since both matrices have the same -main minor. Therefore, . Now, if , then P cannot be the canonical permutation of G. Otherwise, , it is verified that , and then P cannot be the canonical permutation of G. Thus, the theorem becomes true by reductio ad absurdum.

Theorem 2 enacts an interesting linkage between adjacency matrices and spanning trees. Additionally, a new kind of code of tuples is defined keeping the semantics of adjacency matrices. This fact opens new skylines for mixing graph mining results coming from algorithms based on string of labels, for example: FSG (KURAMOCHI, 2001), FFSM (HUAN, 2001), grCAM (GAGO-ALONSO, 2010b), VEAM (ACOSTA-MENDOZA, 2012) and REAFUM (LI, 2015), and other ones based on codes of tuples, for example: gSpan (YAN, 2002) Gaston (NIJSSEN, 2004), MoFa (BORGELT, 2006), and gdFil (GAGO-ALONSO, 2010a).

 

CONCLUSIONS

The main conclusion of this paper is that only connected permutations need to be checked for calculating a kind the canonical adjacency matrix. A theorem supporting such affirmation was stated and mathematically proved. In addition, a characterization of the cardinality of the connected permutation subset was given for specific kind of graphs; including: path, cycles, and complete graphs without only one edge. Thus, the reduction of the cardinality achieved by this subset regarding the whole set of permutations was emphasized. Additionally, the proof of this characterization for paths shows a relationship among graph mining, graph theory and k-tope numbers coming from discrete mathematics. These properties could be used, in future work, for speeding up the redundancy checking in graph mining, since a reduction of the number of iterations could be attained.

Additionally, the main idea of a previously published work (BORGELT, 2006), establishing connections between two existing kinds of canonical form based on tuple code, is expanded by including the link with canonical adjacency matrix. This fact was supported by a new theorem stated and proved in this paper. Moreover, the above linkage is achieved by means of the underlying code, a novel codification strategy for labeled graphs.

Future work will be devoted to implement computational algorithms for canonical form detection, taking advantage of the novel mathematical framework. In this sense, we are trying to enrich the already reported pruning strategies, for example the proposed one in the Nauty algorithm (MCKAY, 1981), by considering connected permutation prefixes. Besides, some hybrid approaches between string of labels and tuple codes will be designed and tested.

 

REFERENCES

ACOSTA-MENDOZA, N.; GAGO-ALONSO, A.; MEDINA-PAGOLA, J.E. Frequent approximate subgraphs as features for graph-based image classification. Knowledge-Based Systems, 2012, 27, 381-392.

BORGELT, C. Canonical forms for frequent graph mining. In: 30th Annual Conference of the German Classification Society, Universitat Berlin, Springer-Verlag, 2006, 337-349.
CONWAY, J.; GUY, R. The Book of  Numbers. New York, Copernicus, Springer-Verlag, 1996. 310 pages. BAPAT, R. Graphs and Matrices. New Delhi, Hindustan Book Agency, India, 2010. 171 pages

DIESTEL, R. Graph Theory. Electronic Edition, Springer-Verlag, New York, 2000.

GAGO-ALONSO, A.; MEDINA-PAGOLA, J.E.; CARRASCO-OCHOA, J.A.; MARTÍNEZ-TRINIDAD, J.F. Full duplicate candidate pruning for frequent connected subgraph mining. Integrated Computer-Aided Engineering, 2010a, 17(3): 211-225.

GAGO-ALONSO, A.; PUENTES-LUBERTA, A.; CARRASCO-OCHOA, J.A.; MEDINA-PAGOLA, J.E.; MARTÍNEZ-TRINIDAD, J.F. A new algorithm for mining frequent connected subgraphs based on adjacency matrices. Intelligence Data Analysis, 2010b, 14 (3), 385-403.

HARARY, F.: Graph Theory. Addison-Wesley, Reading, MA, 1969, 178-180.

HUAN, J.; WANG, W.; PRINS, J. Efficient mining of frequent subgraphs in the presence of isomorphism. In: 3rd IEEE International Conference on Data Mining, Melbourne, FL, IEEE Computer Society, 2003, 549-552.

INOKUCHI, A.; WASHIO, T.; MOTODA, H. An apriori-based algorithm for mining frequent substructures from graph data. In: 4th European Conference on Principles of Data Mining and Knowledge Discovery, Lyon, France, Springer-Verlag, 2000, 13-23.

JIANG, C.; COENEN, F.; ZITO, M. A survey of frequent subgraph mining algorithms, The Knowledge Engineering Review, 2013, 28: 75-105.

KURAMOCHI, M.; KARYPIS, G. Frequent Subgraph Discovery. In: 1st IEEE International Conference on Data Mining, San Jose, CA, IEEE Computer Society, 2001, 313-320.

LI, R.; WANG, W.: REAFUM: Representative Approximate Frequent Subgraph Mining. In: SIAM International Conference on Data Mining, Vancouver, BC, Canada, 2015. ISSN 2167‐0099.

MANSO, M.; PELLINO, S.; PETROSINO, A.; ROZZA, A. A Novel Graph Embedding Framework for Object Recognition.  In: Computer Vision - ECCV 2014 Workshops, 2014, 341-352.

MCKAY, B. D. Practical graph isomorphism. Congressus Numerantium, 1981, 30: 45-87.

NIJSSEN, S.; KOK, J.N. A quickstart in frequent structure mining can make a difference. In: 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, Washington, ACM, 2004, 647-652.

VO, B.; NGUYEN, D.; NGUYEN, T.L. A Parallel Algorithm for Frequent Subgraph Mining. In: International Conference on Computer Science, Applied Mathematics and Applications, Metz, France, 2015, 163-173.

 

Recibido: 19/09/2014
Aceptado: 15/06/2015