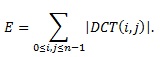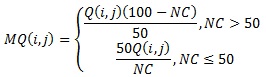Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Ciencias Informáticas
versión On-line ISSN 2227-1899
Rev cuba cienc informat vol.10 no.2 La Habana abr.-jun. 2016
ARTÍCULO ORIGINAL
Algoritmo esteganográfico de clave privada en el dominio de la transformada discreta del coseno
Steganographic algorithm of private key on the domain of the cosine discrete transform
Anier Soria Lorente1 , Ramiro A. Cumbrera González1, Yunior Fonseca Reyna1*
1 Departamento de Informática, Universidad de Granma, Km 18 ½ Carretera Manzanillo, Bayamo, Granma, Cuba,{asorial, rcumbrerag, fonseca} @udg.co.cu
*Autor para la correspondencia: fonseca@udg.co.cu
RESUMEN
La Esteganografía con clave privada, es un sistema similar a sistemas criptográficos de cifras simétricas. En este artículo es objetivo presentar un nuevo algoritmo esteganográfico que utiliza una clave privada, vinculado al domino de la frecuencia usando la transformada discreta del coseno, que permite generar una nueva secuencia binaria a partir del mensaje e indica las posiciones donde serán insertados los elementos de dicha secuencia. Con el algoritmo propuesto se mejora el nivel de imperceptibilidad del esteganograma analizado a través de los resultados obtenidos de los parámetros: Relación Señal a Ruido Pico, entropía relativa y coeficientes de correlación por pares de histogramas entre el esteganograma y la imagen que sirve de cubierta, en comparación con los resultados de métodos previamente propuestos en la literatura.
Palabras clave: Clave privada, esteganografía, imagen digital, seguridad de la información.
ABSTRACT
The private key steganography is a system similar to the cryptographic system of symmetric figure. In this paper, is objective to show a new steganographic algorithm, that use a private key, linked with frequency domain using discrete cosine transform, generate a new binary sequence from the message to hide and suggest the positions where will be inserted the binary sequence elements. The proposed algorithms improvement the imperceptibility, analyzed through obtained results of parameters: peak signal to-noise ratio, relative entropy (Er) and the correlation coefficients of histograms pairs of the steganogram and the cover image, comparing with the results of the methods proposed in the literature.
Key words: Steganography, DCT domain, digital image, information security, private key.
INTRODUCCIÓN
En la ciencia de la información, se definen la esteganografía como el conjunto de técnicas que permiten ocultar cualquier tipo de información dentro de otra, de forma tal que la presencia de un mensaje no puede ser detectada con técnicas convencionales. Es usada principalmente en la Seguridad de la Información y permite burlar la vigilancia electrónica en el Internet o simplemente, que terceras personas no tengan acceso a la información(Chang, et al., 2002; Fan, et al., 2011; Li y Wang, 2007; Wong, et al., 2007) .
La esteganografía utiliza medios digitales, tales como archivos de texto, audio, imagen y video, que son utilizados como transporte para ocultar la información, a este medio se le conoce como contenedor o cubierta (C). Cuando el mensaje secreto es ocultado en una cubierta, mediante una técnica esteganográfica, se obtiene un esteganograma que contendrá el mensaje ocultado(Ioannidou, et al., 2012; Noda, et al., 2006) , sin que levante alguna sospecha de su existencia. Una vez que los datos han sido encubiertos, la información puede ser transferida a través de medios de comunicación inseguros.
No hay que confundir la criptografía con la esteganografía: la primera modifica los datos para hacerlos incomprensibles, mientras que la segunda simplemente los oculta dentro de otros datos. A pesar del enfoque diferente de cada una, en muchas ocasiones se combinan ambas técnicas para lograr mejores resultados. Las razones para el uso de la esteganografía pueden ser muy variadas, dentro de ellas están: porque no existe soporte para encriptar los datos o una autoridad que no permite el paso de cierta información. Cuando se usa la esteganografía, la información transita en los medios sin que pueda ser detectado el contenido de lo que se oculta en su interior(Duric, et al., 2005; Lou y Liu, 2002; Song, et al., 2011; Wang, et al., 2010) .
Los métodos usados en la esteganografía se pueden dividir en dos categorías: los correspondientes al dominio espacial y los del dominio de frecuencias (Chan, et al., 2002). La aplicación de la esteganografía en el dominio espacial, radica en que los algoritmos son utilizados en la manipulación de los píxeles y en la inserción de la información secreta en los bits menos significativos o bien de mayor redundancia.
El dominio de la frecuencia está vinculado a los cambios de las altas y bajas frecuencias de la imagen, de forma tal que las altas frecuencias como los bordes, las líneas y ciertos tipos de ruidos son utilizados para ocultar información. Dentro de esta técnica se utilizan transformadas tales como la de Fourier(Cheddad, et al., 2010), la transformada discreta de los cosenos(Chang, et al., 2002; Li y Wang, 2007; Noda, et al., 2006; Velasco, et al., 2007; Wong, et al., 2007; Yu y Babaguchi, 2008) y el de wavelet (Zhiwei, et al., 2007).
En general, los métodos en el dominio espacial tienden a proporcionar mayor capacidad de inserción que los métodos en el dominio de la frecuencia, sin embargo, estos últimos son más robustos contra posibles ataques tales como: compresión, recorte o algún procesamiento de imagen (Soria-Lorente, et al., 2013; Soria-Lorente, et al., 2014).
Un método esteganográfico muy usado es la de modificación de los bits menos significativos(Fridrich, et al., 2002; Velasco, et al., 2007), lo cual constituye una manera fácil para insertar información, sin embargo, tiene como desventaja la de ser altamente vulnerable a pequeñas modificaciones en la cubierta. Un atacante puede simplemente aplicar técnicas de procesamiento de señales con el fin de destruir completamente el mensaje secreto y en muchos casos, usando un sistema de pérdida de compresión, produce el deterioro total de la información.
Recientemente se ha notado (Soria-Lorente, et al., 2014), en el sistema de desarrollo de la esteganografía, que fijar información en el dominio de frecuencia de una señal puede ser mucho más robusto que insertarla en el dominio del tiempo. Los sistemas esteganográficos robustos, conocidos en la actualidad, realmente operan en alguna clase del dominio de la transformada.
Una forma de aplicar la esteganografía, en el dominio de la transformada, es explotar el proceso de la compresión de JPEG, el cual incluye una cuantización de coeficientes a través de la DCT. La compresión de JPEG es acertada porque cambia drásticamente los coeficientes de alta frecuencia, para los cuales el ojo humano es en gran parte insensible, mientras que altera ligeramente los de frecuencia baja. Estos elementos han sido usados, por algunos autores, para aumentar el nivel de imperceptibilidad de la transformación en la imagen usada (Fan, et al., 2011; Li y Wang, 2007; Yu y Babaguchi, 2008) .
En el procesamiento de imágenes digitales, la DCT en dos dimensiones está definida de la siguiente manera: considerando un bloque de tamaño nxm de una imagen f, entonces la transformada discreta del coseno viene dada mediante la ecuación:
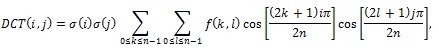
donde los coeficientes ![]() toman los valores:
toman los valores:
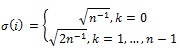
Mientras que su transformada inversa IDCT viene dada por:
![]()
donde, para ambas transformadas, tanto directa como inversa, se tiene que ![]() Además, los coeficientes de la DCT bidimensional de un bloque de imagen de 8x8 píxeles, están organizados de la siguiente manera: el primer coeficiente DCT corresponde al coeficiente DC o de frecuencia cero, mientras que el resto de los coeficientes pertenece a los coeficientes AC o de mayor frecuencia.
Además, los coeficientes de la DCT bidimensional de un bloque de imagen de 8x8 píxeles, están organizados de la siguiente manera: el primer coeficiente DCT corresponde al coeficiente DC o de frecuencia cero, mientras que el resto de los coeficientes pertenece a los coeficientes AC o de mayor frecuencia.
En el 2007, Wong y Tanaka, señalan que la DCT es muy utilizada en compresión de imágenes y presenta su modelo Mod4(Wong, et al., 2007). Esta transformada cuenta con una buena propiedad de compactación de energía y es muy similar a la transformada de Karhunen-Loève (Pajares y de la Cruz, 2001), que produce coeficientes no correlacionados, con la diferencia de que los vectores base de la DCT dependen sólo del orden de la transformada seleccionado y no de las propiedades estadísticas de los datos de entrada (Chang, et al., 2002).
En el presente artículo, los autores inspirados en un trabajo de Velasco y otros autores(Velasco, et al., 2007), proponen un nuevo algoritmo esteganográfico correspondiente al dominio de la frecuencia. La diferencia con el anterior, reside en que se hace uso de una clave privada, la cual propicia que el mensaje secreto sólo pueda ser descifrado por el receptor que porte de la misma.
En el 2002 Chang et al., han utilizado determinados elementos que se incluyen en el algoritmo que se explica más adelante, como son: recorrido en zigzag, la clave privada para cifrar el mensaje y la matriz de cuantificación para los coeficientes de la DCT(Chang, et al., 2002), con el fin de ocultar un mensaje en una cubierta constituida por una imagen JPEG en niveles de grises (8 bits). El algoritmo propuesto, enriquece la idea anterior, porque utiliza como cubierta una imagen con extensión BMP de 24 bits que contiene los planos R, G y B (Red, Green y Blue por sus siglas en inglés), y una clave privada.
MATERIALES Y MÉTODOS
La eficiencia en la protección de la información, mediante la esteganografía, radica precisamente en el uso de un algoritmo adecuado que posibilite de forma correcta la inserción de datos dentro de una cubierta. Para lograr un buen nivel de imperceptibilidad, un sistema esteganográfico tiene que generar un esteganograma lo suficientemente inocente y que no levante ninguna sospecha a simple vista. Una de las formas de conseguirlo es usando una clave privada.
En un sistema esteganográfico, la clave privada es similar al cifrado simétrico, en el que el remitente escoge una cubierta y oculta el mensaje mediante la clave seleccionada, de forma tal que, si esta es conocida por el receptor, él puede conseguir la información secreta del esteganograma mediante un proceso de extracción. Evidentemente, la esteganografía de clave privada requiere del intercambio de dicha clave, aquí es precisamente donde entra a jugar un papel fundamental, la criptografía asimétrica o de clave pública(Hideki, 2003; Yuan, et al., 2010).
La clave diseñada, genera una nueva secuencia binaria a partir del mensaje secreto e indica aquellos componentes AC donde serán insertados los elementos de dicha secuencia binaria.
Proceso de Inserción
A continuación, se expone el algoritmo para el proceso de inserción de datos dentro de una cubierta.
1. Solicitar una clave de 64 bits al usuario.
1.1 Particionar la secuencia binaria de la clave secreta facilitada por el usuario, en bloques de 16 bits.
2. Modificar la secuencia binaria del mensaje secreto del siguiente modo:
2.1 Particionar la secuencia binaria del mensaje secreto en bloques de 64 bits. En caso en que la longitud del mensaje secreto no sea divisible por 8, completar con cualquier valor hasta que se haya alcanzado dicha divisibilidad.
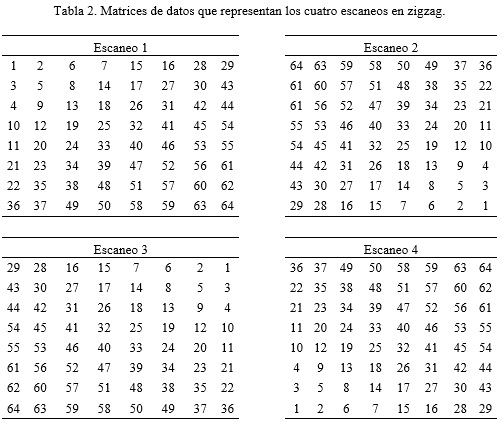
2.2 Realizar el correspondiente mod( i - 1,4) + 1 escaneo en zigzag (Tabla 1), al i-ésimo bloque de 64 bits conseguido en el paso anterior, obteniéndose de este modo un nuevo i-ésimo bloque de 64 bits, donde i varía desde 1 hasta n, suponiendo que representa la cantidad de bloques de 64 bits obtenidos en 2.1.
2.3 Aplicar la siguiente operación
entre cada uno de los 4 sub-bloques de 16 bits del i-ésimo bloque de 64 bits conseguido en el paso anterior y el mod( i - 1,4) + 1 bloque binario de 16 bits de la clave secreta, obteniéndose de este modo un nuevo i-ésimo bloque de 64 bits, donde i varía desde 1 hasta n.
2.4 Concatenar cada uno de los bloques de 64 bits conseguidos en el paso 2.3, para así conseguir una nueva secuencia binaria, la cual será ocultada en la cubierta, como se describirá en los pasos que siguen a continuación.
3. Segmentar la cubierta en bloques de 8x8 píxeles. Las imágenes RGB por cada píxel tienen 3 bytes, es decir, un byte para cada plano, por tal motivo, un bloque de 8x8 píxeles equivalente a 3 matrices cuadradas de orden 8.
4. Convertir al dominio de la frecuencia a través de la DCT, cada una de las 3 matrices cuadradas de orden 8correspondientes a cada uno de los bloques de 8x8 píxeles, conseguidos en el paso 3, siguiendo un recorrido de izquierda a derecha y de arriba hacia abajo.
5. Calcular la energía de cada una de las matrices cuadradas de orden 8 conseguidas en el paso anterior, mediante la ecuación
6. Seleccionar aquellas matrices cuadradas de orden 8 cuya energía sea mayor que un umbral dado (U).
7. Dividir cada elemento de las matrices seleccionadas, en el paso anterior, por cada elemento de la siguiente matriz de cuantificación, dada con relación al factor de calidad de compresión, por:
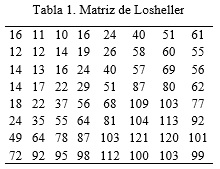
donde, Q(i , j) es la matriz siguiente que se muestra en la tabla 1, conocida como matriz de Losheller (Sourish, et al., 2015 ):
8. Realizar un escaneo según el primer movimiento en zigzag, a cada matriz resultante del paso anterior, obteniéndose de este modo un vector de longitud 64, cuyo primer elemento corresponde al coeficiente DC o de frecuencia cero, mientras que el resto de los elementos corresponde a los coeficientes AC de mayor frecuencia.
9. Insertar los elementos de la secuencia binaria, resultantes del paso 2.4, en los bits menos significativos de los primeros 8 elementos AC obtenidos en el paso 8, siempre y cuando el correspondiente elemento mod 64 de la secuencia binaria de la clave secreta sea igual a 1. Al mismo tiempo, se debe tener en cuenta el signo del elemento AC, en caso de que sea negativo se obtiene el valor absoluto y luego de la inserción se conserva el signo. De esta forma, se consigue una matriz cuadrada de orden 8 luego de reordenarse el vector de longitud 64 resultante de la inserción.
10. Multiplicar cada matriz resultante del paso anterior, por la matriz de cuantificación del paso 7 y luego aplicar la inversa de la DCT para así construir la imagen, obteniéndose de este modo el esteganograma. Ver tabla 2
Proceso de Extracción
A continuación, se expone el algoritmo para el proceso de extracción.
A continuación, se expone el algoritmo para el proceso de extracción.
-
Solicitar una clave de 64 bits al usuario.
-
Segmentar el esteganograma en bloques de 8x8 píxeles.
-
Convertir al dominio de la frecuencia a través de la DCT cada una de las 3 matrices cuadradas de orden 8, correspondientes a cada uno de los bloques de 8x8 píxeles obtenidos en el paso 2, siguiendo un recorrido de izquierda a derecha y de arriba hacia abajo.
-
Calcular la energía (ver paso 5 del proceso de inserción), de cada una de las matrices cuadradas de orden 8 conseguidas en el paso 3.
-
Seleccionar aquellas matrices cuadradas de orden 8 cuya energía sea mayor que un umbral dado.
-
Dividir cada elemento de las matrices seleccionadas en el paso anterior, por cada elemento de la matriz de cuantificación del paso 7 del proceso de inserción.
-
Realizar un escaneo según el primer movimiento en zigzag (Tabla 1 A), a cada matriz resultante del paso 6, obteniéndose un vector de longitud 64, cuyo primer elemento corresponde al coeficiente DC o de frecuencia cero, mientras que el resto de los elementos corresponde a los coeficientes AC de mayor frecuencia.
-
Extraer los bits menos significativos del valor absoluto de los primeros 8 elementos AC obtenidos en el paso 7, siempre y cuando el correspondiente elemento, mod 64 de la secuencia binaria de la clave secreta sea igual a 1.
-
Formar una secuencia binaria con los resultados del paso anterior. En el caso de que la longitud de esta secuencia binaria no sea divisible por 64, completar los bits con cero o uno hasta que se haya alcanzado la divisibilidad.
-
Particionar la secuencia binaria resultante del paso anterior en bloques de 64 bits.
-
Particionar la secuencia binaria de la clave secreta, facilitada por el usuario, en bloques de 16 bits.
-
Suponiendo que n representa la cantidad de bloques de 64 bits conseguidos en el paso 10, aplicar la siguiente operación
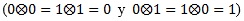 , entre cada uno de los 4 sub-bloques de 16 bits del
, entre cada uno de los 4 sub-bloques de 16 bits del  -ésimo bloque de 64 bits conseguido en el paso 10 y el entre cada uno de los 4 sub-bloques de 16 bits del i-ésimo bloque de 64 bits conseguido en el paso 10 y el mod( i - 1,4) + 1, bloque binario de 16 bits de la clave secreta, obteniéndose de este modo un nuevo i-ésimo bloque de 64 bits, donde i varía desde 1 hasta n.
-ésimo bloque de 64 bits conseguido en el paso 10 y el entre cada uno de los 4 sub-bloques de 16 bits del i-ésimo bloque de 64 bits conseguido en el paso 10 y el mod( i - 1,4) + 1, bloque binario de 16 bits de la clave secreta, obteniéndose de este modo un nuevo i-ésimo bloque de 64 bits, donde i varía desde 1 hasta n. -
Realizar el correspondiente mod( i - 1,4) + 1 escaneo en zigzag, al i-ésimo bloque de 64 bits conseguido en el paso anterior, obteniéndose de este modo un nuevo i-ésimo bloque de 64 bits, donde i varía desde 1 hasta n.
-
Particionar la secuencia binaria resultante, del paso 13, en bloques de 8 bits, los cuales representan cada uno de los bytes del mensaje secreto.
RESULTADOS Y DISCUSIÓN
Para las evaluaciones y resultados del algoritmo esteganográfico propuesto y el análisis de las ventajas con respecto al de Velasco y otros autores (Velasco, et al., 2007), se implementó la aplicación en MatLab ® 7.14 (MathWorks, 2012) STEGLAB 1.0 (no registrado), que permite calcular las magnitudes que más adelante se exponen.
Una medida de la distorsión es la PSNR, esta es muy común en el procesamiento de una imagen y su utilidad reside en dar una relación del grado de supresión de ruido entre la cubierta y el esteganograma, proporcionando de esta manera una medida de calidad. El PSNR, dado en decibelios (dB), se calcula por la ecuación:
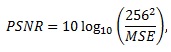
donde MSE es el error cuadrático medio:
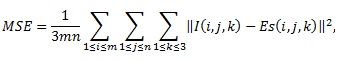
siendo I la cubierta y Es el esteganograma.
La seguridad de un sistema esteganográfico es evaluada tras examinar la distribución de la cubierta y del esteganograma. (Cachin, 1998), propuso una medida que cuantifica la seguridad del sistema esteganográfico llamada ![]() - seguro, la cual viene dada mediante la expresión:
- seguro, la cual viene dada mediante la expresión:

donde PE y PC son las probabilidades de distribución de los histogramas de la cubierta y del esteganograma respectivamente. La última expresión representa la entropía relativa entre las dos probabilidades de distribución PE y PC.
Cabe notar que un sistema esteganográfico se llama perfectamente seguro si ![]() sin embargo, conforme aumenta la cantidad de información que se oculta, aumenta al mismo tiempo la robustez, por lo cual la entropía también aumenta, de forma tal que la seguridad de un sistema esteganográfico es obtenida a través de un valor
sin embargo, conforme aumenta la cantidad de información que se oculta, aumenta al mismo tiempo la robustez, por lo cual la entropía también aumenta, de forma tal que la seguridad de un sistema esteganográfico es obtenida a través de un valor ![]() , para cualquier tipo de imagen (Cachin, 1998).
, para cualquier tipo de imagen (Cachin, 1998).
Los coeficientes de correlación fueron calculados dividiendo las cubiertas y los esteganogramas en sus matrices componentes R, G y B. La correlación se realizó con los pares de histogramas para el plano rojo (Rr), verde (Rg) y azul (Rb), utilizando las funciones de MatLab® 7. 14 e implementadas en la aplicación STEGLAB 1.0.
Se diseñaron dos experimentos para la validación del algoritmo y la comparación de los valores de las magnitudes del de clave privada, con los obtenidos por el método de Velasco (MV) y otros autores (Velasco, et al., 2007).
Primer experimento
Para el desarrollo del primer experimento, se tomó la imagen “Lenna” (ver Figura 1), en la aplicación STEGLAB 1.0 y usando el método de Velasco y otros autores (una de las opciones del sistema) y se ocultó el siguiente mensaje secreto: “Gauss es uno de los más importantes matemáticos de la historia. Los diarios de su juventud muestran que ya en sus primeros años había realizadograndes descubrimientos en teoría de números, un área en la que su libro Disquisitiones arithmeticae marca el comienzo de la era moderna”, obteniéndose así el esteganograma.
Posteriormente, utilizando la misma imagen, se encubrió el mensaje siguiendo el algoritmo de clave privada implementado en el software antes mencionado y se obtuvo nuevamente otro esteganograma. Para los esteganogramas obtenidos se calcularon el PSNR, los coeficientes de correlación por pares y la entropía relativa Er usando valores de U = 200, los niveles de calidad en 50, 55, 70, 75 y 77 y la clave “NQLK-7a$” de 64 bits.
Los valores obtenidos de las magnitudes mencionadas se muestran en la Tabla 3 Cuando se usó la clave privada, los valores de PSNR aumentaron para cada uno de los niveles de calidad y con respecto a los obtenidos para el modelo MV, lo que demostró que la imperceptibilidad se hizo mayor. Sin embargo, los valores de coeficientes de correlación disminuyeron ligeramente para los planos rojo y verde (Rr y Rg), manteniéndose constante en el azul (Rb), esto evidenció un mayor efecto de la clave los planos rojo y verde que es por donde comienza a distribuirse la información secreta.
Por otra parte, los valores de la entropía relativa (Er) para cada nivel de calidad, aumentaron cuando se usó la clave privada, lo cual pudo ser debido a la correspondencia de esta magnitud con la distribución de la información que realizó dicha clave, cuando generó la secuencia aleatoria para ubicar el mensaje secreto en la imagen. Los valores de Er, variaron de un nivel de calidad a otro y, en el caso de los planos, existieron diferencias porque se supone que a cada uno de ellos le correspondió diferente información del mensaje secreto. En todos los casos los valores obtenidos para Er, en cada uno de los planos, son cercanos a cero; por lo que se puede afirmar que el sistema esteganográfico con el algoritmo propuesto estuvo cercano al ideal.
Los valores de PSNR, utilizando un valor de umbral inferior (U= 200) al propuesto por (Velasco, et al., 2007), resultaron ser mayores para diferentes niveles de calidad; de esta forma se puede afirmar que el uso de la clave privada, con las funciones que tiene dentro del algoritmo, aumentó la imperceptibilidad en el esteganograma de la imagen de Lenna.
Segundo experimento
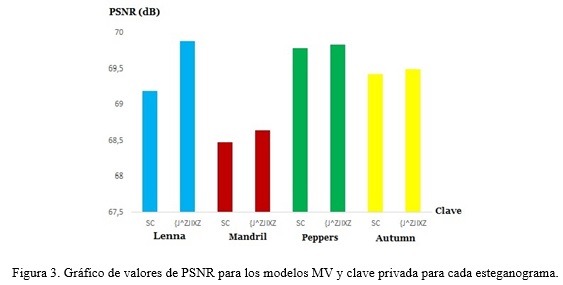
En el segundo experimento se utilizó la misma aplicación y se calcularon las magnitudes utilizadas en el experimento anterior para un umbral de 200 y un nivel de calidad de 77, para lograr los esteganogramas con el texto del mensaje usado anteriormente, correspondientes a las imágenes Lenna, Mandril, Peppers y Autumn, cada una con dimensiones 1120 x 784 (Figura 2). Los valores obtenidos por los dos métodos se compararon haciendo uso de los algoritmos: de Velasco y utilizando la clave “{J^ZJIXZ” de 64 bits.
La Tabla 4, muestra los valores de las magnitudes calculadas. Se observa, que para cada una de las imágenes utilizadas, existieron incrementos del PSNR con el uso del algoritmo propuesto comparado con el que no usa clave (SC) siendo mucho más acentuado en la imagen de Lenna (Figura 3), lo cual puede estar relacionado con la diferente ubicación de la información secreta cuando se usó la clave privada, es decir, en el esteganograma de Lenna quedó ocultado el mensaje con una mayor imperceptibilidad que en el resto de las imágenes usadas, por lo que se demostró que en este proceso, existe influencia de las imágenes utilizadas como cubiertas.
Por otra parte, fue significativo que los coeficientes de correlación para el plano B tuvieran valores igual a la unidad, lo que indica que hay plena correspondencia entre los histogramas de las cubiertas y los correspondientes a los esteganogramas, en el resto de los planos los coeficientes sufrieron sólo una ligera modificación para la imagen de Lenna y Autumn, no obstante, se mantuvieron cercanos a la unidad.
Por otra parte, la entropía relativa (Er) aumentó en todos los planos para las imágenes de Lenna, Mandril y Autumn, sin embargo, en la imagen Peppers disminuyeron los valores para los planos G y B. Este último fue un resultado lógico si se tiene en cuenta que existe un incremento de la información en cada una de las matrices y los movimientos internos a que fueron sometidas las cubiertas utilizadas.
Por último, se tomaron diferentes valores de umbral (superiores a 200) y un factor de calidad de 50, en todos los casos se coincidió con los propuestos por Velasco y otros autores (2007). El mensaje ocultado fue el mismo que en el primer experimento al igual que la clave. Los resultados obtenidos se muestran en la Figura 4.
Otra característica fue que dos de los esteganogramas obtenidos, “Peppers” y “Lenna”, no tuvieron variaciones del PSNR, cuando se incrementó el umbral, sin embargo, en “Autumn” existió un ligero incremento de 60,87 a 60,88 para los dos últimos valores, lo cual pudo ser debido a la forma diferente en que se distribuyó la información en la cubierta cuando se usó la clave privada, sin embargo, se puede pensar en que dicho incremento no debe influir notablemente en el aumento de la imperceptibilidad de la información oculta en dicha cubierta.
Finalmente, podemos decir que en este experimento, con el aumento del umbral no existen variaciones perceptibles del PSNR y no limita de ningún modo la aplicación efectiva del algoritmo propuesto.
CONCLUSIONES
Este artículo ha presentado un nuevo algoritmo esteganográfico con clave privada en el dominio de la DCT, cuya finalidad es ocultar textos secretos en una imagen RGB. El mismo es novedoso si se considera la secuencia binaria que se genera y que indica exactamente las posiciones donde se ubicará la información secreta en la cubierta.
Se realizaron dos experimentos que demostraron que para valores distintos de umbral y del nivel de calidad, los PSNR resultaron ser mayores que los obtenidos por Velasco y otros autores. Los esteganogramas son mucho más seguros usando el algoritmo propuesto en el dominio de la DCT. De acuerdo con los valores de entropía relativa, se puede afirmar que se acercan a los esteganogramas ideales o perfectos.
Los valores de PSNR dependen de las características de las imágenes que se escogieron como cubierta, del nivel de calidad y el valor de umbral usado. Finalmente, en la mayoría de los casos analizados los coeficientes de correlación fueron iguales a la unidad o muy cercanos a ella, también, los valores de entropía relativa tuvieron un ligero aumento con respecto al modelo MV, por lo que se puede decir que el algoritmo propuesto es factible de aplicar en la práctica.
REFERENCIAS BIBLIOGRÁFICAS
CACHIN, C. An Information-Theoretic Model for Steganography. En: Proceedings of 2nd Workshop on Information Hiding. USA: Springer, 1998, p. 1 -12.
CHANG, C. C., CHEN, T. S., Y CHUNG, L. Z. A steganographic method based upon JPEG and quantization table modification. Information Sciences, 2002, 141: p. 123-138.
CHEDDAD, A., CONDELL, J., CURRAN, K., Y MCKEVITT, P. A hash-based image encryption algorithm. Optics Communications, 2010, 283(6): p. 879-893.
DURIC, Z., JACOBS, M., Y JAJODIA, S. EN: E. J. W. C.R. RAO Y J. L. SOLKA. Handbook of Statistics. Elsevier, 2005. Volume 24, p. 171-187
FAN, L., GAO, T., YANG, Q., Y CAO, Y. An extended matrix encoding algorithm for steganography of high embedding efficiency. Computers & Electrical Engineering, 2011, 37(6): p. 973-981.
FRIDRICH, J., GOLJAN, M., Y DU, R. Lossless data embedding-new paradigm in digital watermarking. Special Issue on Emerging Applications of Multimedia Data Hiding, 2002, 1(2): p. 185-196.
HIDEKI, N. Fundamentos Matemáticos da Criptografia Quântica. Universidade Federal de Mato Grosso, Cuiabá, MT- Brasil, 2003.
IOANNIDOU, A., HALKIDIS, S. T., Y STEPHANIDES, G. A novel technique for image steganography based on a high payload method and edge detection. Expert Systems with Applications, 2012, 39(14): p. 11517-11524.
LI, X., Y WANG, J. A steganographic method based upon JPEG and particle swarm optimization algorithm. Information Sciences, 2007, 177(15): p. 3099-3109.
LOU, D.-C., Y LIU, J.-L. Steganographic Method for Secure Communications. Computers & Security, 2002, 21(5): p. 449-460.
NODA, H., NIIMI, M., Y KAWAGUCHI, E. High-performance JPEG steganography using quantization index modulation in DCT domain. Pattern Recognition Letters, 2006, 27(5): p. 455-461.
PAJARES , G., Y DE LA CRUZ, J. M. En: Visión por computador: imágenes digitales y aplicaciones. Madrid: In RA-MA 2001. p. 643-723
SONG, S., ZHANG, J., LIAO, X., DU, J., Y WEN, Q. A Novel Secure Communication Protocol Combining Steganography and Cryptography. Procedia Engineering, 2011, 15: p. 2767-2772.
SORIA-LORENTE, A., SÁNCHEZ, R., Y RAMÍREZ, A. Steganograohic algorithm of private key. Revista de Investigación G.I.E. Pensamiento Matemático, 2013, 3(2): p. 059-072.
SORIA-LORENTE, A., MECÍAS, R., PÉREZ, A., Y RODRÍGUEZ, D. Pseudo-asymmetric steganography algorithm. Lect. Mat., 2014, 35(2): p. 183-196.
SOURISH, M., MOLOY, D., ANKUR, M., NIRUPAM, S., Y RAFIQUL, I. DCT based Steganographic Evaluation parameter analysis in Frequency domain by using modified JPEG luminance Quantization Table. Journal of Computer Engineering, 2015, 17(1): p. 68-74.
VELASCO, C. L., LÓPEZ, J. C., NAKANO, M., Y PÉREZ, H. M. Esteganografía en una imagen digital en el dominio DCT. Científica, 2007, 11( 4): p. 169-176.
WANG, Y., LIU, J., ZHANG, W., Y LIAN, S. Reliable JPEG steganalysis based on multi-directional correlations. Signal Processing: Image Communication, 2010, 25(8): p. 577-587.
WONG, K., QI, X., Y TANAKA, K. A DCT-based Mod4 steganographic method. Signal Processing, 2007, 87(6): p. 1251-1263.
YU, X., Y BABAGUCHI, N. Breaking the YASS Algorithm via Pixel and DCT Coefficients Analysis. IEEE, 2008: p. 1-4.
YUAN, F., HU, Y.-P., WANG, Y., Y OU, H.-W. Cryptanalysis of dragon scheme The J. of China Universities of Posts and Telecommun., 2010, 17( 4): p. 80-87
ZHIWEI, K., JING, L., Y YIGANG, H. Steganography based on wavelet transform and modulus function. Journal of Systems Engineering and Electronics, 2007, 18(3): p. 628-632.
Recibido: 17/11/2014
Aceptado: 18/04/2016