My SciELO
Services on Demand
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista Cubana de Ciencias Informáticas
On-line version ISSN 2227-1899
Rev cuba cienc informat vol.12 no.3 La Habana July.-Sept. 2018
ARTÍCULO ORIGINAL
Desempeño de los métodos de detección de señales con modulación QPSK en sistema GFDM para 5G.
Performance of the detection method of signal with QPSK modulation in GFDM system for 5G.
Randy Verdecia Peña1*
1Departamento de Eléctrica, Centro de Telecomunicaciones (CETUC), Pontificia Universidad Católica de Rio de Janeiro, Brasil. randy.verdecia@cetuc.puc-rio.br
*Autor para la correspondencia: randy.verdecia@cetuc.puc-rio.br
RESUMEN
La demanda del mercado actual exige que las redes de comunicaciones móviles necesiten un aumento de su tasa de transmisión, así como, la calidad de los servicios. Debido a este hecho los investigadores del área trabajan sobre la tecnología que utilizarán en la capa física de la siguiente generación de la red celular 5G. El sistema de Multiplexación por División de Frecuencia Generalizada (GFDM) es una de las candidatas para la capa físicas de esta tecnología. El objetivo de esta investigación es evaluar el desempeño de una selección de métodos para la detección del sistema GFDM en 5G. En este trabajo fue descrito el sistema GFDM, así como, los métodos de detección Zero Forcing, Filtro Casado y Cancelación de Interferencia Paralela. Las curvas de desempeños resultantes de aplicar los métodos de detección son presentadas para canal Gaussiano y Fijo además son comparadas con el sistema Multiplexación por División de Frecuencias Ortogonales. Se tiene como resultado que, para los dos casos de canales, el desempeño del sistema GFDM para los detectores Zero Forcing y Filtro Casado con Cancelación Paralela de Interferencia, tienen el mismo comportamiento que el sistema Multiplexación por División de Frecuencias Ortogonales detectado con Zero Forcing. Se concluye que el mejor método de detección es el Filtro Casado con Cancelación Paralela de Interferencia porque presenta menos complejidad computacional para la recuperación de la señal enviada por el transmisor.
Palabras clave: canal de comunicación, comunicaciones móviles, sistema de transmisión GFDM, métodos de detección.
ABSTRACT
Current market demand requires that mobile communication networks need an increase in their transmission rate, as well as, the quality of services. Due to this fact, researchers in the area are working on the technology they will use in the physical layer of the next generation of the 5G cellular network. The Generalized Frequency Division Multiplexing (GFDM) system is one of the candidates for the physical layer of this technology. The objective of this research is to evaluate the performance of a selection of methods for the detection of the GFDM system in 5G. In this work, the GFDM system was described, as well as, the Zero Forcing, Matched Filter and Parallel Interference Cancellation methods. The performance curves resulting from applying the detection methods are presented for Gaussian and Fixed channels also they are compared with the Orthogonal Frequency Division Multiplexing system. As a result, for the two channels cases, the performance of the GFDM system for the Zero Forcing and Matched Filter detectors with Parallel Interference Cancellation have the same behavior as the Orthogonal Frequency Division Multiplexing system detected with Zero Forcing. It is concluded that the best detection method is the Matched Filter with Parallel Interference Cancellation because it has less computational complexity when it comes to recovering the signal sent by the transmitter.
Key words: communication channel, mobile communications, GFDM system of transmission, detection methods.
INTRODUCCIÓN
Las comunicaciones móviles se han convertido en una herramienta fundamental en nuestras vidas. Desde su inicio con la red de primera generación (1G) hasta la actualidad, el número de clientes, demanda de servicios y aplicaciones; se han incrementado de forma exponencial (Farhang-Boroujeny, 2011). Para satisfacer estas necesidades los estándares de tecnología móvil han migrado hacia la era digital haciendo una transformación general de sus sistemas (Öztürk, Basar, y Çırpan, 2017), ( Duangsuwan y Jamjareegulgarn, 2017).La primera generación tuvo como principal característica la transmisión de voz. Por otro lado, la segunda generación móvil (2G) aumentó su capacidad mediante la digitalización de la voz, así como, la duración de la batería de los dispositivos portátiles. Las principales características que introduce esta generación celular son: la mayor Calidad de Servicio (Quality of Service, QoS) y Servicios de Mensajería Corta (Short Menssage Service, SMS), provocando un revolucionario impacto para los clientes (Feryando , Suryani, y Endroyono, 2017). La tercera generación (3G) proporcionó un paso de avance debido al servicio de internet en el dispositivo portátil.
A medida que las aplicaciones necesitaban de mayores requerimientos y los clientes aumentaron sus demandas, fue necesario el incremento de la velocidad en las redes existentes, por tal motivo surge la cuarta generación (4G) (Michailow, et al., 2014). La tecnología 4G utiliza en la capa física la forma de onda de Multiplexación por División de Frecuencia Ortogonales (Orthogonal Frequency Division Multiplexing, OFDM) cumpliendo las espectativas del mercado para la que fue pensado en su inicio. La principal característica de OFDM es la utilización de Prefijo Cíclico (Cyclic Prefix, CP) (Browning, et al., 2017), constituyendo a la vez una desventaja significativa para los requerimientos de la siguiente generación celular. Debido a la ineficiencia espectral que provoca el CP entre cada paquete, se identifica como una mala elección para aplicaciones multiusuarios donde qualquier pérdida de sincronización entre los involucrados conduce a una reducción en el desempeño del sistema (Morelli , Kuo, y Pun, 2007), (Farhang-Boroujeny, 2011), (Farhang Boroujeny y Moradi, 2015).
Las nuevas capacidades demandadas por los clientes es un desafío para investigadores y desarrolladores de la tecnología móvil. Varias formas de ondas han sido propuestas para la quinta generación de la red móvil (5G), una de las tecnología candidata es la Multiplexación por División de Frecuencia Generalizada (Generalized Frequency Division Multiplexing, GFDM) (Melgarejo, Kumar, Fraidenraich, y Mendes, 2018). GFDM utiliza para realizar la transmisión un solo CP para varios time-slots (División en intervalo de tiempo), permitiendo una mayor eficiencia espectral comparada con otras tecnologías como OFDM. Este sistema es empleado para aplicaciones con baja latencia y prevee ser flexible para diferentes escenarios de 5G (Matthe, Zhang, y Fettweis, 2016).
La señal transmitida mediante GFDM es detectada en el receptor, quien se encarga de recuperar la información enviada. Los métodos de detección comunes en los sistemas de transmisión digital son: Zero-Forcing (ZF), Filtro Casado (Matched Filter, MF) y Mínimo Error Medio Cuadrático (Minimum Mean Square Error, MMSE). El análisis del desempeño de estos sistemas permiten brindar una evaluación de su eficiencia espectral (Melgarejo, Kumar, Fraidenraich, y Mendes, 2018). Estos métodos en conjunto con el Cancelamiento Paralelo de Interferencia (Pararell Interference Cancellation, PIC) logran obtener un mejor desempeño de los sistema digitales ( Zhang, Ahmed, y Kim, 2017), (Hama y Ochiai, 2016). Dado a la eficiencia espectral mediante el empleo de un solo CP por paquetes de datos el objetivo de esta investigación es la evaluación del desempeño de los métodos de detección ZF, MF, ZF-PIC y MF-PIC en un sistema GFDM con mudulación Quadrature Phase Shift Keying (QPSK) en canales gaussianos (AWGN) y fijos. Con la evaluación del desempeño se puede observar cual de los detectores presentan menor probabilidad de error con respecto a la relación señal a ruido.
Para la evaluación del desempeño en el sistema GFDM fueron realizados diferentes estudios. La caracterización de la modulación QPSK a utilizar fue el primer paso. En segundo lugar, se detalla el modelo matricial del sistema de transmisión GFDM, así como, las diferentes técnicas para la detección de la señal transmitida. Son caracterizados los canales a utilizar y presentado el desempeño en los diferentes ambientes, para determinar cuál presenta mayor rendimiento.
MATERIALES Y MÉTODOS
Modulación QPSK
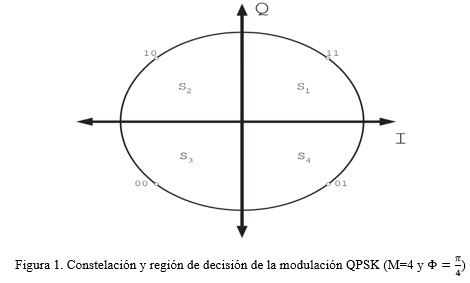
La modulación QPSK envuelve el uso de cuatro fases. Generalmente son equidistante entre sí y representan los dígitos 00, 01, 11, 10, cada fase transmite dos bits. La asignación de bits por cada símbolo transmitido es realizada mediante código de Gray (entre dos símbolos adyacentes, los símbolos solo se diferencian en 1 bit), permite lograr minimizar la tasa de bits erróneo. La modulación QPSK puede identificarse como la suma de dos señales Binary Phase Shift Keying (BPSK) con portadoras en cuadraturas desfasadas (Verdecia, 2018), estas dos señales son independientes. El diagrama de la constelación y región de decisión es mostrado en la figura 1:
La modulación QPSK emplea la mitad del ancho de banda en comparación con la modulación BPSK con la misma velocidad de transmisión o transmitir al doble de la velocidad, aprovechando todo el ancho de banda del sistema GFDM (Chirag, Lohith, y Prashantha, 2017). La probabilidad de error está dada por la ecuación (1):
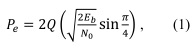
donde Q(.) representa la función que determina la probabilidad de error de una variable aleatoria gaussiana, Eb es la energía de bit y N0 caracteriza el nivel espectral de ruido en el receptor. El relacionamiento ![]() es conocido como relación señal a ruido.
es conocido como relación señal a ruido.
Transmisor GFDM
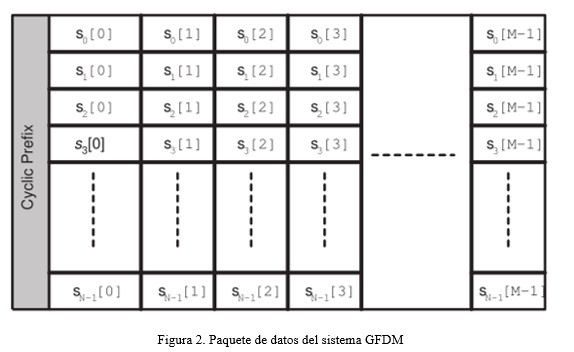
GFDM es un sistema multi-portadora que utiliza un solo CP para la transmisión de un bloque de símbolos, siendo su ecualización en el lado del receptor de baja complejidad (Fettweis, Krondorf, y Bittner, 2009). La estructura del paquete GFDM es presentado en la figura 2, donde los datos de los símbolos son extendidos en tiempo y frecuencia como en el sistema OFDM (Farhang-Boroujeny y Moradi, 2015). El paquete de datos GFDM como es ilustrado en la figura 2 está conformado por un único CP, cada columna representa la cantidad de subportadoras, mientras que las filas son los time slots, motivo por el cual el sistema de transmisión GFDM transmite M*N símbolos de datos por bloque de transmisión.
La figura 3 representa el modelo de transmisión y recepción del sistema GFDM. Su proceso de transmisión es descrito como sigue: para transmitir la información binaria, el primer paso es la codificación de la información. El segundo paso es la realización de la modulación en banda base, que este trabajo utiliza QPSK. Luego los símbolos modulados complejos son particionados en bloques que contienen elementos, donde es el número de time-slots y es el número de sub-portadoras (Fettweis, Krondorf, y Bittner, 2009), (Sendrei y Marchevsky, 2015).
Dado el desenvolvimiento realizado en Farhang-Boroujeny y Moradi, 2015) los símbolos de datos de entrada Sk [n] y la iFFT de salida son relacionada con la siguiente ecuación:
![]()
donde Se [n] puede ser expresado con la expresión (3),
![]()
donde ![]() es un vector fila de ceros y
es un vector fila de ceros y ![]() es una matriz circulante cuya primera columna está compuesta por la fórmula (4):
es una matriz circulante cuya primera columna está compuesta por la fórmula (4):
![]()
F-1 es la matriz de Transformada de Fourier Discreta Inversa (inverse Discrete Fourier Transform, iDFT) de dimensión MN x MN. La ecuación (2) puede ser reescrita con la siguiente ecuación:
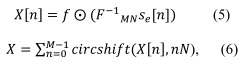
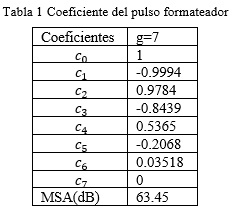
donde ![]() corresponde al espectro discreto del pulso formateador. La selección de los mismos es de gran importancia para el desempeño del sistema. En esta investigación fueron utilizados los coeficientes determinados en (Mirabbasi y Martin, 2003) y son mostrados en la tabla (1), donde g es la cantidad de coeficientes empleados.
corresponde al espectro discreto del pulso formateador. La selección de los mismos es de gran importancia para el desempeño del sistema. En esta investigación fueron utilizados los coeficientes determinados en (Mirabbasi y Martin, 2003) y son mostrados en la tabla (1), donde g es la cantidad de coeficientes empleados.
Alternativamente, X[n] puede ser calculado de forma matricial como en la ecuación (7):

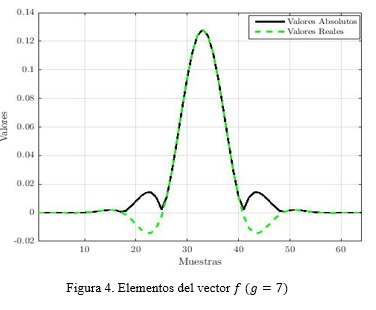
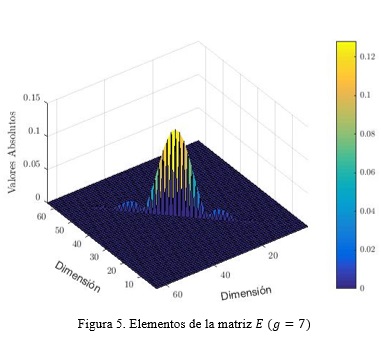
con E=diag(f), donde diag(f) es una matriz diagonal cuya diagonal principal está compuesta por el vector f. La figura 4 representa los valores reales y absolutos del vector f y la figura 5 ilustra la conformación de la matriz diagonal E, donde la diagonal está compuestas de los valores absolutos de la figura 4.
La ecuación (7) es posible porque ![]() puede ser obtenida apilando productos repetidos de
puede ser obtenida apilando productos repetidos de ![]() entonces (7) puede ser escrito con la expresión:
entonces (7) puede ser escrito con la expresión:
![]()
donde IN representa una matriz idéntica de tamaño N. Por su parte la matriz Z es dada por la expresión (9):
Siendo ![]() luego una forma alternativa de la ecuación (6) está dada por:
luego una forma alternativa de la ecuación (6) está dada por:
![]()
Donde la matriz CnN es tal que su multiplicación por un vector de tamaño N es equivalente a realizar la operación de desplazamiento circular de período nN en ese vector. Reescribiendo (10) en forma matricial y teniendo presente (8) como en ( Mayoral, Sampaio, y Pereira, 2017), se obtiene la ecuación (11):
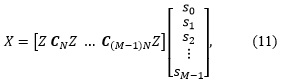
donde ![]() Una simplificada fórmula del vector de transmisión X, en el sistema GFDM puede ser representado como la multiplicación de la matriz por los símbolos del vector de datos, como la ecuación (12):
Una simplificada fórmula del vector de transmisión X, en el sistema GFDM puede ser representado como la multiplicación de la matriz por los símbolos del vector de datos, como la ecuación (12):
![]()
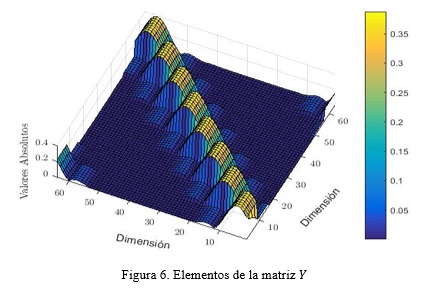
siendo Sa el vector que tiene los M vectores de símbolos de N elementos organizados en el paquete GFDM. La figura 6 ilustra los valores de la matriz Y de transmisión del sistema en cuestión.
Una vez obtenido el modelo matemático del sistema GFDM, es realizado la detección de la señal transmitidas utilizando diferentes técnicas. Con estos métodos es posible evaluar el desempeño del sistema GFDM. En las secciones siguientes son descritos cada uno de ellos.
Detector Zero Forzing en GFDM
Esta sub-sección describe el proceso de detección Zero Forcing al sistema GFDM. Una vez adicionado el CP en el transmisor, la información pasa por el canal de comunicación y al llegar al receptor este es removido, modelándose de la siguiente forma matricial:
![]()
donde ![]() es el vector ruido gaussiano blanco aditivo (Additive White Gaussian Noise, AWGN) con
es el vector ruido gaussiano blanco aditivo (Additive White Gaussian Noise, AWGN) con ![]() como la varianza (Jardak, Ahmed, y Alouini, 2012), la matriz H representa la matriz del canal de dimensión MN x MN y Y es la matriz de transmisión del sistema GFDM con dimensión MN x MN. La detección ZF es aplicada a la matriz A+ de dimensión MN x MN que representa el producto de A+= H * Y cómo se muestra en la expresión (14):
como la varianza (Jardak, Ahmed, y Alouini, 2012), la matriz H representa la matriz del canal de dimensión MN x MN y Y es la matriz de transmisión del sistema GFDM con dimensión MN x MN. La detección ZF es aplicada a la matriz A+ de dimensión MN x MN que representa el producto de A+= H * Y cómo se muestra en la expresión (14):
![]()
La matriz es dada por A+ZF= A+-1 y es multiplicada por el vector Rgfdm obteniendo la siguiente expresión:
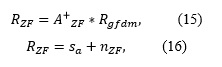
donde nFZ representa el ruido resultante que afecta a los símbolos recibidos. A partir de la ecuación (16) una estimativa de los símbolos puede ser obtenida por medio del siguiente algoritmo.
Detector Matched Filter en GFDM
A partir de la expresión (13) es realizada la detección de Filtro Casado (Matched Filter, MF) al sistema GFDM para recuperar los símbolos transmitidos. El método de detección MF en la matriz es aplicada a la matriz A+ . El resultado de la aplicación del método de detección al vector Rgfdm recibido, resulta la siguiente expresión:
![]()
A continuación, es detallado a partir de la expresión (17), el algoritmo de detección MF en el sistema GFDM.
Detector ZF-PIC en GFDM
Es importante en el desempeño del sistema GFDM escoger el pulso formateador dado que, de este depende la presencia de las interferencias tales como: Interferencia entre Símbolos (Interference Symbols, ISI) e Interferencia entre Sub-portadoras (Interference Carrier, ICI). Un método que es utilizado para realizar la cancelación de las interferencias generadas en este sistema es la Cancelación de Interferencia en Paralelo (Parallel Interference Cancellation, PIC).
La forma para la implementación del PIC puede ser expresado por la ecuación (18):
![]()
donde la estimativa es determinada por la expresión (19):
![]()
donde ![]() , representa nuevos vectores de los cuales pueden ser obtenidas nuevas estimativas de los símbolos transmitidos en el sistema GFDM a partir de la estimativa anterior. El término
, representa nuevos vectores de los cuales pueden ser obtenidas nuevas estimativas de los símbolos transmitidos en el sistema GFDM a partir de la estimativa anterior. El término ![]() representa la implementación del MF en el vector recibido. (A+HA+) 0 es la matriz resultante del producto del hermitiano de la matriz A+ versus ella y el resultado de esta con la diagonal principal de ceros. Para la implementación de este método de cancelación de interferencia es tomada la primera estimativa ZF y después por medio de recursiones del PIC se generan secuencialmente nuevas estimativas. Estas son sometida a la medida de máxima verosimilitud que en este caso corresponde a la Métrica de Menor Distancia metric of less distance, MD dada por la ecuación (20):
representa la implementación del MF en el vector recibido. (A+HA+) 0 es la matriz resultante del producto del hermitiano de la matriz A+ versus ella y el resultado de esta con la diagonal principal de ceros. Para la implementación de este método de cancelación de interferencia es tomada la primera estimativa ZF y después por medio de recursiones del PIC se generan secuencialmente nuevas estimativas. Estas son sometida a la medida de máxima verosimilitud que en este caso corresponde a la Métrica de Menor Distancia metric of less distance, MD dada por la ecuación (20):
![]()
Las estimativas son generadas y el proceso es interrumpido en la j-esimo iteración ![]() siempre que
siempre que ![]() , por tanto la estimativa final es
, por tanto la estimativa final es ![]() A continuación, es presentado un algoritmo que describe el proceso de detección ZF-PIC.
A continuación, es presentado un algoritmo que describe el proceso de detección ZF-PIC.
Detector Matched Filter-PIC en GFDM
Para la implementación del método de detección MF-PIC se pueden seguir los pasos de la sub-sección anterior, siendo la primera estimativa determinada por la aplicación del MF al vector recibido. A continuación, es ilustrado el algoritmo que describe el proceso de detección MF-PIC.
RESULTADOS Y DISCUSIÓN
En esta investigación es analizado el desempeño de la modulación QPSK utilizando diferentes detectores en sistema GFDM por medio de Tasa de Error de Bit (Bit Error Rate, BER). Las figuras que se muestran en esta sección muestran claramente que es posible realizar el relacionamiento entre Signal Noise Ratio (SNR) y BER, donde la (SNR) es definida de 0-10dB. Las curvas ilustran el desempeño del sistema GFDM descrito en la sección anterior cuando es aplicado ZF,MF,ZF-PIC y MF-PIC, con la realización de los 2 últimos de forma recursiva. Para realizar el análisis del desempeño fue realizado un script .m en la herramienta de simulación matemática Matlab. En la tabla 2 es presentado la respuesta al impulso de los canales de comunicación utilizados para evaluar el desempeño del sistema. Para realizar la simulación la respuesta al impulso del canal fue normalizada para energía unitaria.
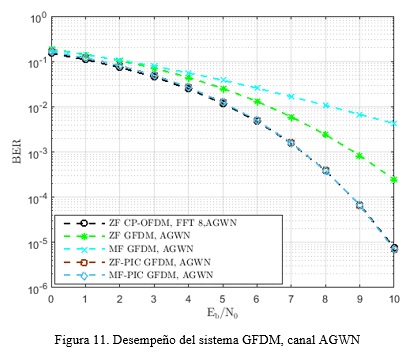
En la figura 11 son presentadas las curvas de desempeños en términos del BER para los diferentes detectores presentados en la sección anterior en presencia del canal AWGN. Para estas curvas se tomó como M=8, N=8, J=3 y A+ = I*Y , siendo I un canal AWGN con respuesta al impulso descrita en la tabla 2. El desempeño del sistema GFDM es comparado con el sistema CP-OFDM después de aplicarle en la detección, el método ZF. Se observa además que el desempeño BER de ZF-PIC y MF-PIC ambos están muy próximo al sistema CP-OFDM.
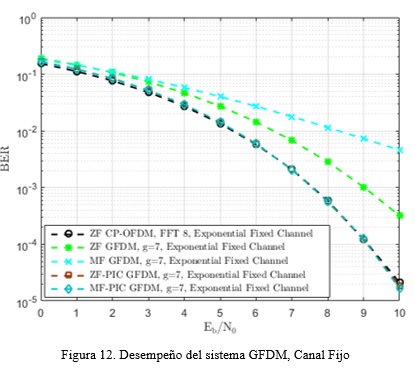
En la figura 12 son mostradas las curvas de desempeños para el caso del Canal Fijo que se describió en la tabla 2. Para estas curvas se toman como J=3 y A+ = H*Y en el sistema GFDM cuando son utilizados los métodos de detección ZF-PIC y MF-PIC. Para validar el comportamiento del desempeño fue comparado con ZF CP-OFDM obteniéndose como resultado que, ZF- OFDM y MF- OFDM tienen un comportamiento similar al ZF CP-OFDM.
Es importante señalar que entre ZF-PIC y MF PIC la segunda técnica tiene gran ventaja debido a su baja complejidad operacional. En el caso del primer método se necesita realizar inversión de matrices que pueden tener alta complejidad computacional. La tabla 3 ilustra la complejidad computacional de los algoritmos de la figura 7 y 8 con respectos a las multiplicaciones complejas, donde se demuestra que MF es menos complejos que ZF.
La baja complejidad de PIC con MF con respecto a ZF-PIC proviene del hecho de que el detector de PIC propuesto requiere el cálculo de la matriz de peso correspondiente a MF solo una vez y MF es presenta menor complejidad computacional que ZF.
CONCLUSIONES
Como resultado de la presente investigación se describieron diferentes algoritmos para la detección de señales en sistema GFDM obteniéndose un modelo teórico para la recuperación de la señal transmitida. Fueron ilustradas curvas de desempeños del sistema GFDM y se compararon con CP-OFDM. El resultado de la comparación demostró que dos de las curvas tienen un comportamiento similar al desempeño del sistema CP-OFDM detectado con ZF. Se concluye también que el método MF-PIC presenta una baja complejidad matemática a la hora de realizar la detección de la información, porque no necesita hacer la inversión de matrices de grandes dimensiones ni cuadradas. Se ha demostrado que el sistema GFDM puede alcanzar desempeños similares al OFDM, pero con una mayor eficiencia espectral debido a la utilización de un solo CP para transmitir la información. Es recomendado para trabajos futuros hacer un estudio para otras condiciones de canales, así como para otras configuraciones y técnicas de detección.
REFERENCIAS BIBLIOGRÁFICAS
Referencias
Browning, C., Farhang, A., Saljoghei, A., Marchetti, N., Vujicic, V., Doyle, L., y Barry, L. (2017). 5G wireless and wired convergence in a passive optical network using UF-OFDM and GFDM. 2017 IEEE International Conference on Communications Workshops (ICC Workshops), pp. 386-392.
Chirag, B., Lohith, A., y Prashantha, H. (2017). Comparative performance analysis of various digital modulation schemes in AWGN channel. 2017 Innovations in Power and Advanced Computing Technologies (i-PACT), pp. 1-5.
Duangsuwan, S., y Jamjareegulgarn, P. (2017). Detection of data symbol in a Massive MIMO systems for 5G wireless communication. 2017 International Electrical Engineering Congress (iEECON), pp.1-4.
Farhang Boroujeny, B., y Moradi, H. (2015). Derivation of GFDM based on OFDM principles. 2015 IEEE International Conference on Communications (ICC), pp. 2680-2685.
Farhang-Boroujeny, B. (2011). OFDM Versus Filter Bank Multicarrier. IEEE Signal Processing Magazine, vol. 28, no. 3, pp. 92-112.
Farhang-Boroujeny, B., y Moradi, H. (2015). Derivation of GFDM based on OFDM principles. 2015IEEE International Conference on Communications (ICC), pp. 2680-2685.
Feryando, D. A., Suryani, T. y Endroyono. (2017). Performance analysis of regularized channel inversion precoding in multiuser MIMO-GFDM downlink systems. 2017 IEEE Asia Pacific Conference on Wireless and Mobile (APWiMob), pp. 101-105.
Fettweis, G., Krondorf, M., y Bittner, S. (2009). GFDM - Generalized Frequency Division Multiplexing. VTC Spring 2009 - IEEE 69th Vehicular Technology Conference, pp.1-4.
Hama, Y., y Ochiai, H. (2016). A low-complexity matched filter detector with parallel interference cancellation for massive MIMO systems. 2016 IEEE 12th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), pp. 1-6.
Jardak, S., Ahmed, S., y Alouini, M. (2012). Generating correlated QPSK waveforms by exploiting real gaussian random variables. 2012 Conference Record of the Forty Sixth Asilomar Conference on Signals, Systems and Computers (ASILOMAR), pp. 1323-1327.
Mayoral, J., Sampaio, R., y Pereira, R. (2017). Detecção e Cancelamento Simultaneo de Interfere}ncia em Paralelo em Sistemas com Transmissão GFDM para 5G. Proc, XXXV Simposio de Telecomunicações e Processamento de Sinal.
Matthe, M., Zhang, D., y Fettweis, G. (2016). Iterative Detection using MMSE-PIC Demapping for MIMO-GFDM Systems. European Wireless 2016; 22th European Wireless Conference, pp. 1-7.
Melgarejo, D., Kumar, S., Fraidenraich, G., y Mendes, L. (2018). Bit Error Probability for MMSE Receiver in GFDM Systems. IEEE Communications Letters, vol. PP, no. 99, pp. 1-1.
Michailow, N., Matthe, M., Gaspar, I., Caldevilla, A., Mendes, L., Festag, A., y Fettweis, G. (2014). Generalized Frequency Division Multiplexing for 5th Generation Cellular Networks. IEEE Transactions on Communications, vol. 62, no. 9, pp. 3045-3061.
Mirabbasi, S., y Martin, K. (2003). Overlapped complex-modulated transmultiplexer filters with simplified design and superior stopbands. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, vol. 50, no.8, pp. 456-469.
Morelli , M., Kuo, C., y Pun, M. (2007). Synchronization Techniques for Orthogonal Frequency Division Multiple Access (OFDMA): A Tutorial Review. Proceedings of the IEEE, vo. 95, no.7, pp. 1394-1427.
Öztürk, E., Basar, E., y Çırpan, H. (2017). Generalized Frequency Division Multiplexing With Flexible Index Modulation. IEEE Access, pp. 24727-24746.
Sendrei, L., y Marchevsky, S. (2015). Nonlinear noise estimation and compensation in GFDM based communication systems for cognitive radio networks. 2015 25th International Conference Radioelektronika (RADIOELEKTRONIKA), pp.313-316.
Verdecia, R. (2018). Análisis del desempeño de los esquemas de modulación BPSK y QPSK para diferentes condiciones de canales en sistema GFDM. Maskay ISSN: 1390-6712, vo. 8, no.1, pp. 7-12.
Zhang, M., Ahmed, S., y Kim, S. (2017). Iterative MMSE-based soft MIMO detection with parallel interference cancellation. IET Communications, vol. 11, pp. 11, pp. 1775-1781.
Recibido: 31/04/2018
Aceptado: 09/07/2018