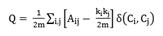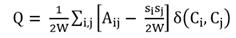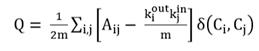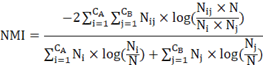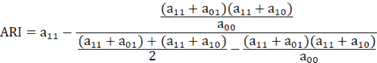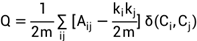INTRODUCTION
Social network represents a set of individuals with relationships among them. In network terms, individuals are represented as nodes and relationships represented with ties (edges) between these individuals. An edge can represent a friendship, or any type of relationship between the individuals linked (Wassernman and Faust.1994). Particularly important in information sciences and scientometrics are the relationship based on authors’ collaborations in a research paper (the collaboration networks) or based in the relationship between author collaboration networks and citation networks. Social network analysis is a method used in bibliometrics and scientometrics for the analysis of collaboration in scientific publications (Otte and Rousseau, 2002).
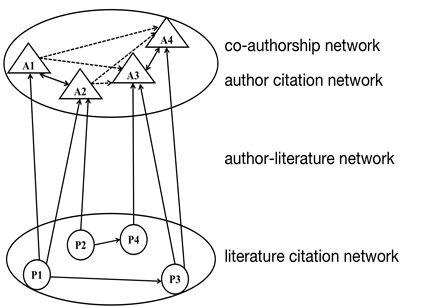
Hybrid network is a heterogeneous network which contains a variety of node types or a variety of relationship types. The concept of heterogeneous network emphasizes the complexity at the level of network structure, while the network formed by the integration of multiple nodes and multiple relationships emphasizes the richness of functions. The characteristics of the multi-node and multi-relationship hybrid network are mainly reflected in the following two aspects: first, the diversity of nodes, including a variety of node types. For example, in the academic network, nodes can be authors, literature, keywords, journals, etc., in the medical network, nodes can be doctors, drugs, patients, etc. Second, the richness of relationships. For example, in an academic network, relationships can include author collaboration, author citation, literature citation and author-literature relationship, etc. In a medical network, relationships can include relationships between doctors prescribing drugs, patients taking drugs and so on.
Mathematically, a social network is a graph (a set of nodes and edges). One common type of graph is a k-partite graph. If k = 2 it is a bipartite graph, in which the vertices are partitioned into k-disjoint subsets, and each edge connects vertices in distinct partitions. Hence a bipartite graph is one in which the nodes can be divided into two sets U and V so that every edge in the graph connects a node in V with a node in U. Studying scientific collaborations networks as well as how papers cite others (citation networks) has become increasingly important. Understanding these networks help us better understand how scientific discoveries and innovations are communicated within the scientific community (Divakarmurthy and Menezes, 2013). On the other hand, clustering (or mapping) of scientific articles is an important area in scientometric research. Clustering analysis is useful for detecting research topics and revealing scientific structure and dynamics, which can aid in systematic understanding of research fields (Wang et al., 2013; Zhang et al, 2016).
Community structure detection is a method used to identify clusters of nodes in a network. Community structure detection is the most widely studied structural features of complex networks. At present, the research on community detection methods of multi-node and multi-relationship hybrid network mainly focuses on the following two kinds: one is to extend the existing algorithm to deal with the hybrid network directly, the other is to reduce the dimension of hybrid network to homogeneous network and then conduct community detection (Shah and Zaman, 2010). Based on the above two ideas, the community detection methods of multi-node and multi-relationship hybrid network mainly fall into the following five categories: probabilistic model-based method, meta-path based method (Sun et al., 2011), seed nodes based method, extend modularity method, and homogeneous method of heterogeneous network (Shi et al, 2017). Probabilistic model-based method usually needs to specify the number of communities according to prior knowledge, which may lead to unstable results. Although the meta-path based method is relatively simple, the similarity obtained is usually a deviation measure. The extend modularity method is still unable to avoid the limitation of the maximization of modularity, which is the resolution limitation, so it cannot detect small communities in large-scale networks. For the method based on seed nodes, there are still some problems about how to select effective seed nodes efficiently. Although the homogeneous method of heterogeneous network is easy to understand, the derivation process of the model is complicated and the implementation complexity is too high. It can be seen that there is still a lot of room for further research on community detection methods of hybrid network.
Here, we present a review about the method of community detection in hybrid network, and the application to the academic network analysis. Our objective is to introduce to the reader in the most important concepts on the community detection topics, the most common techniques used and the future development of this emergent field. This paper is organized as follow: In Computational Methodology we present an overview about the construction of a hybrid academic network with several relationships. We also introduce the concept of modularity and its definition for different types of networks. In the Results and Discussion section we present some of the most relevant papers in the domain of Network Community Detection. Besides of the most popular techniques to perform network community detection are discussed. Finally, we briefly introduce examples of the literature in this field.
Computational Methodology
The source of the revised articles was de Web of Science database during the period 1980-2021. In our revision, we have prioritized the conceptual and theoretical papers on the field of network community detection, particularly the application to academic networks. Based on the Web of Science database, the retrieval formula was TS= ((hybrid network OR heterogeneous network) AND (community detection OR community discovery)). Up to April 29, 2021, 625 literatures were retrieved. We focus on the literatures related to community detection in multi-node and multi-relation hybrid networks. 228 of the recovered articles are proceedings paper and the rest are articles (original researches in periodical journals or books chapter).
Definition of hybrid networks
The definition of network has been emerging endlessly. Complex networks (Newman, 2003) refer to a network with some or all of the properties like self-organization (Watanabe et al., 2015), self-similarity (Song et al., 2005; Gallos et al., 2013), attractor, small world phenomenon (Gallos et al., 2012), and scale-free degree. Since general network diagram cannot reflect the network structure truly and effectively, Estrada et al. (2006) introduced super networks, which can more accurately describe complex network structures. A heterogeneous network is a special type of network (Sun et al., 2009), which contains a variety of node types and relationship types. The corresponding homogeneous networks refer to the network containing only one node type and relationship type (Wolfe et al., 1993). Based on the above definitions, the concept of a hybrid network is adopted in this study, that is, a network containing multiple node types or multiple relationship types. Both complex networks and super networks point to a wide range of networks, which refer to a network that exhibits a high degree of complexity. Hybrid networks essentially belong to the category of heterogeneous network, but heterogeneous networks emphasize the complexity of network topology. It pays more attention to heterogeneous relations and pays less attention to isomorphic relations between nodes of the same type (Ran et al., 2013), Hybrid networks emphasize the mixing of multiple nodes and multiple relationships, fully consider heterogeneous relationships and isomorphic relationships, and reflect the richness of functions. Therefore, the definition of "hybrid networks" is adopted in this study; researchers can focus on the improvement of function instead of just focusing on the construction of network topology, in the case that it is more consistent with the real network.
Constructing a hybrid network
First, we present an example of how two nodes of literature and author are selected to construct a hybrid network that includes four relationships among literature citation, author collaboration, author citation, and literature-author (as shown in Figure 1). Construct a co-authorship network based on the co-authors of literature, construct a literature citation network and author citation network based on the citation relationship between literature, and construct an author-literature bipartite network based on the affiliation between authors and literature (Figure 1). This network can not only reveal the vertical information in the time axis, but also present the "horizontal" correlation in the wide space, which shows the basis and internal dynamic mechanism of the author relationship construction.
RESULTS AND DISCUSSION
Relevant Community Detection Studies
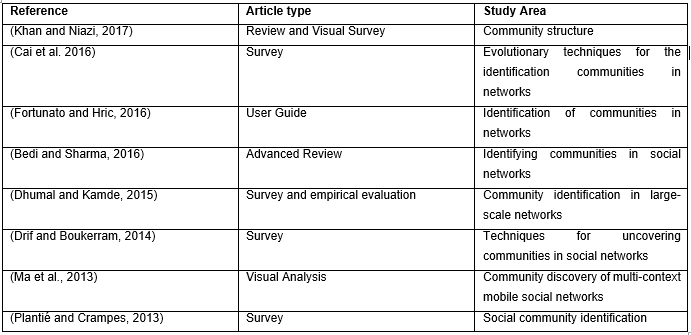
Community detection has involved an enormous consideration due to the growing availability of the data sets of the large-scale networks, particularly social and academic networks. To provide insightful information about community detection, much research has been conducted in the form of surveys, systematic literature reviews, and visual studies. But, only a few of them shows how the field advanced over time. To demonstrate the sense of details, information about existing literature is listed in Table 1 (Khan and Niazi, 2017).
Table 1 Some representative papers on the domain of “Network Community Detection”. Structure and some of the papers were selected from Ref. (Khan and Niazi, 2017).
Community Detection Techniques
Modularity
For the mathematical formulation of this subsection, we have followed (Khan and Niazi, 2017).
Usually, the techniques to find optimal communities in reasonably fast time are based on the optimization of objective functions. Modularity optimization is one of the most widely used techniques among them.
For unweighted networks, modularity Q can be defined as:
In Eq. 1:
m is the number of links, k is the degree of vertex i, k is the degree of vertex j, Ci is the community to vertex i, Cj is the community to vertex j, and if i and j belong to the same community, otherwise it equals to 0.
For weighted networks, modularity Q can be defined as:
In Eq. 2, W is total weight of all of the links in the network, Wij is the weight of the links between vertices i and j, si is the strength of vertex i, s is the strength of vertex j. Also, if i and j belong to the same community, otherwise it equals to 0 (Khan and Niazi, 2017).
If we consider now a weighted and direct network, the modularity is defined by (Arenas et al. 2007) as:
In overlapping communities (unweighted and directed networks and unweighted and undirected networks) Shen et al. introduce the formulas showed in Figure 2:
A new quantitative measure named as modularity density (D), which is based on the density of subgraphs has been defined to solve community structure of networks (Li et al., 2008). The modularity density is defined as:
Where, Vi is the subset of V i=1, …, m, such that and
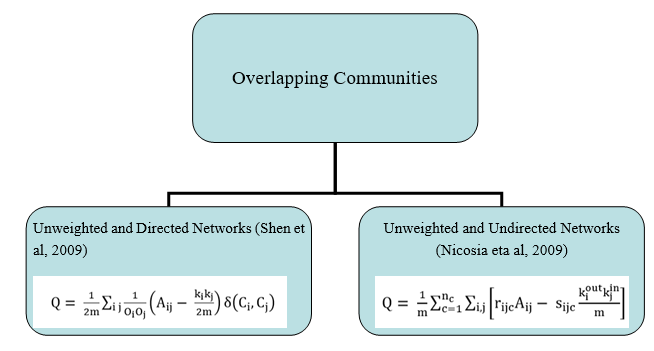
Fig. 2 Definition of modularity (Q) for unweighted and directed networks and unweighted and undirected networks.
Figure 2Other important issue is to know the most common used data set for identification of communities. A representative sample of these data set was reported in (Khan and Niazi, 2017). Thus, we only mention some examples: Southern women dataset (18 nodes), JAZZ musician network (198 nodes and 2742 links), Condense Matter collaboration network (Cond-Mat) (23133 nodes and 93497 links), ego-Facebook (4039 nodes and 88234 links), Lancichinetti-Fortunato-Radicchi, and DBLP (26950 nodes and 88742 links).
Overview about the Community Detection Techniques
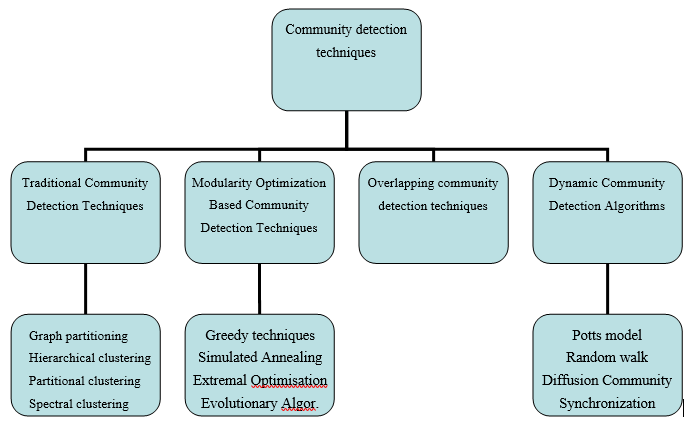
Knowledge of the community structure is critical to comprehend network functionality. Nevertheless, community detection is computationally intractable in large-scale networks. Thus, there are numerical algorithms and techniques to optimize this process. In this section we introduce some of the most relevant techniques. A resume of the most used techniques is presented in Figure 3.
Now, we present an overview of some of these techniques:
Traditional Community Detection Techniques
Graph partitioning: This technique divides the graph into g clusters of predefined size, such that the number of links in a cluster is denser than the number of edges between the clusters (Fortunato 2010).
Hierarchical clustering: These techniques are based on the vertex similarity measure. They do not need a predefined size and number of communities. They can be better represented by dendrograms (Papadopoulos, 2010).
Partitional clustering: It partitions a dataset into a predefined number of k non-overlapping clusters. The aim of this technique is to divide the data points into k clusters in order to optimize the cost function based on dissimilarity measure between nodes (Jin and Han, 2011; Fortunato, 2007, 2010; Dhumal and Kamde, 2015)
Spectral clustering: It includes all techniques which use eigenvectors of matrices to divide the set of data points based on the pairwise similarity between them (Fortunato 2010; Dhumal and Kamde 2015).
Divisive algorithms: It removes inter-cluster edges in a network based on low-similarity to separate communities from each other (Murata, 2010).
Modularity Optimization Based Community Detection Techniques
Greedy techniques: It is an agglomerative technique, where initially, each node belongs to a distinct module, then they are merged iteratively based on the modularity gain. It has a time complexity of O(n)3 on sparse networks.
Simulated Annealing: It has used simulated annealing-based modularity optimization approach and it is a discrete stochastic approach used for the global optimization of the given objective function (Guimera and Amaral, 2005).
Extremal Optimization: This technique is focused on the optimisation of local variables. Duch et al. in (Duch and Arenas 2005) have used it for modularity optimization.
Spectral Optimization: It refers to the use of eigenvectors and eigenvalues of the modularity matrix for
modularity optimization (Fortunato 2010).
Overlapping community detection techniques
One of the most intricate problem of the community detection occurs when an overlapping system is present (it is when most of the nodes simultaneously belong to multiple communities). At present, it is a very common situation. The most known technique used for the identification of overlapping communities in the network is the clique percolation. The motif of this technique is that cliques are more probable to be formed from internal edges which are densely connected than from external edges which are sparsely connected. The communities are made up of k-cliques which refer to the complete subgraphs with k vertices. Communities are formed of k-cliques (which states the complete subgraphs with k vertices). The he k-clique community is the giant component formed of all the adjacent k-cliques which are connected as a k-clique series (Macropol and Singh 2010).
Dynamic Community Detection Algorithms
Potts model: It is based in a generalization of the Ising model in statistical physics. Here, the Potts spin variables can be mapped to the nodes of the graph having community structure. From interactions between neighboring spins, it is plausible that community structure may be identified from like-valued spin clusters of the system, as there will be more interactions in the community and fewer interactions outside the community.
Random walk: The walker starts to walk inside a community from a node and at each time step it moves to the neighboring node selected randomly and uniformly (Hughes, 1996).
Synchronization: It is an emerging phenomenon which has received interest from different fields. It occurs in interacting units and is persuasive in nature, technology and society. In a synchronized state, the system units remain in same or alike states over time. Synchronization is also used in community detection in networks.
In large-scale complex networks, Leader-driven community detection algorithms (LdCD hereafter) is a new trend in devising algorithms. The main idea of this is to identify some particular nodes in the target network, called leader nodes, around which local communities can be computed. As it is based on local computations, they are particularly attractive to handle large-scale networks (Yakoubi and Kanawati, 2014).
Multi-node and multi-relationship hybrid networks community detection methods
At present, the research on community detection methods of multi-node and multi-relationship hybrid networks mainly focuses on the following two kinds: one is to extend the existing algorithm to deal with the hybrid networks directly, the other is to reduce the dimension of hybrid network to homogeneous network and then conduct community detection (Berlingerio et al., 2011; Suthers et al., 2013; Tang et al., 2010). Based on the above two ideas, the community detection methods of multi-node and multi-relationship hybrid networks mainly fall into the following five categories: probabilistic model-based methods, meta-path based methods, seed nodes based methods, extend modularity methods, and homogeneous methods of heterogeneous networks methods.
Probabilistic model-based methods
In the method based on the probabilistic model, some algorithms combine the ranking problem with the community detection problem, which is complementary to each other. RankClus (Sun et al., 2009) algorithm is the earliest proposed ranking clustering algorithm based on hybrid networks, but it is only applicable to two types of nodes. Sun and Han (2009) proposed a new algorithm, NetClus, based on RankClus algorithm, which uses Links between multiple nodes to generate high-quality network clusters. This algorithm has better clustering effects, but it is only applicable to the star network structure, and the representative objects in the data set need to be known in advance. In this regard, the RankClass (Ji et al., 2011) algorithm is improved to be suitable for hybrid networks of any network mode, and can make full use of the label information of any data object. In order to reveal the evolution process of each type of node, Gupta et al. (2011) proposed the EnetClus algorithm, which performs an evolutionary clustering and uses a time smoothing method to display clusters that change over time. Qiu et al. (2015) proposed the OcdRank algorithm, which has low time complexity and supports incremental data updating.
Since the ranking-based method needs to set the number of communities in advance, it is instability. To this end, Sengupta and Chen (2015) proposed a hybrid network spectral clustering method for random block models, and applied the variational EM algorithm for a posteriori reasoning suitable for large networks, allowing different types of nodes to have multiple membership relationships, but this algorithm does not solve the problem of overlapping communities.
Therefore, it can be seen that the methods based on probabilistic models include two methods: ranking-based method and probabilistic statistical model. Although it is developed comprehensively, it is difficult to be applied to large-scale networks due to its high complexity in time and space. In addition, most communities need to be specified according to prior knowledge. When the network is large, it is difficult to predict accurately. And the effectiveness of community detection depends on the estimated number of communities in advance, which leads to instability of the results.
Meta-path based methods
Multiple types of nodes are connected by multiple links. The links linking different nodes contain different semantics. Such links form meta-paths. A meta-path is a series of object types that represent A semantic relation between two nodes (Li et al., 2018), it is an effective semantic capture tool that can capture rich semantic information in hybrid networks (Sun et al., 2011; Shi et al., 2017).
PathSim (Shi et al., 2017) is the earliest proposed algorithm based on meta-path. This algorithm is proposed for homogeneous networks and performs well in measuring the similarity between nodes of the same type. Li et al. (2018) pointed out that most of the meta-path-based hybrid networks community detection methods have two problems. One is that the similarity directly obtained from the meta-path is usually a deviation measure, and the other is how to fuse the similarity of different meta-paths. Therefore, based on the standardization of PathSim to eliminate similarity deviations, they designed a flexible fusion mechanism to dynamically optimize the results, so that the results of community detection are better. Shi et al. (2012) proposed a similarity algorithm (HeteSim), that can measure the same or different types of nodes based on meta-paths. This algorithm calculates similarity through a two-way random walk, and performs better in query and clustering tasks than traditional algorithms, however, HeteSim is only applicable to a single meta-path environment, cannot capture multiple semantic information in a heterogeneous information network, and due to its high complexity, it’s not suitable for large-scale networks. Subsequently, Meng et al. (2014) proposed a double random walk process based on a given meta-path and a reverse meta-path to calculate the similarity of two objects (AvgSim), which can be applied in large-scale networks, and has better clustering effect.
Different meta-paths contain different information, and the selection of different meta-paths will lead to different community detection results. How to determine the number of selected meta-paths or the optimal meta-paths among multiple meta-paths is a difficult problem. Sun et al. (2013) proposed the Pathselclus algorithm, which can assign different weights to different meta paths in hybrid networks. Shi et al. (2017) introduced the random walk method HRank, which is based on meta-paths to evaluate the importance of nodes and meta-paths, and the experimental results showed the unique advantages of meta-paths.
From the above analysis, it can be seen that the meta-path-based community detection methods in hybrid networks are mostly improved by the homogeneous network PathSim method. The meta-path-based method is relatively simple and easy to understand, but the similarity obtained is usually a deviation measure (Li et al., 2018). Moreover, different meta-paths contain different information, so it is still a difficult problem how to accurately calculate the similarity between nodes to show rich semantic correlation, and how to select the optimal meta-path among multiple meta-paths to obtain the optimal partition effect.
Seed nodes based methods
Seed nodes-based methods have become an emerging trend in community detection methods (Hmimida and Kanawati, 2015). The basic idea of the method based on seed nodes is to identify certain specific nodes in the network, called seed nodes, and then build communities around these nodes (Kanawati, 2011; Papadopoulos et al., 2010; Shah and Zamn, 2010).
Yakoubi first proposed the seed node driven community detection algorithm (Licod). The basic idea is to select nodes with higher centrality than most direct neighbors as seed nodes, conduct local community calculation around these nodes, and then conduct community detection from local community sets (Yakoubi et al., 2014). However, this algorithm is only applicable to homogeneous networks. Hmimida and Kanawati (2015) extended the Licod algorithm to hybrid networks, called mux-Licod. This method considers the different types of relationships between nodes in different layers of hybrid networks, and the experimental results show that this method had good practicability.
Seed nodes-based method is a partial calculation method, which is easy to understand and suitable for processing large-scale networks and dynamic networks (Yakoubi et al., 2014). However, there is still no consensus on how to choose effective seed nodes efficiently. In addition, when merging non-seed node communities, there will be be problems of excessive merger of large communities and excessive number of small communities.
Extend modularity methods
Modularity was first used to evaluate the results of community detection. With the deepening of research, community detection algorithms based on modularity appeared (Newman and Girvan, 2004; Tang et al., 2009; Nicosia et al., 2009). Newman et al. first proposed the modularity optimization algorithm FN, which regards each node as a community and calculates the modularity value after the combination of two communities. The community combination methods of increasing the largest or decreasing the smallest in the modularity value is adopted, and the community detection is completed by iteration until the modularity does not increase any more (Newman and Girvan, 2004). However, this algorithm is only applicable to single-node networks.
Guimerà et al. (2007) proposed an extended modularity algorithm suitable for bipartite networks, which can independently identify nodes with similar output connections and nodes with similar input connections, but it is not universal. Murata proposed a modularity algorithm suitable for k-core networks (Murata and Ikeya, 2010). This algorithm has the resolution limitation problem that general modularity algorithms have, and it is not suitable for hybrid networks with general morphology. Liu et al. (2014) proposed a composite modularity method. Its core idea is to decompose a heterogeneous network into multiple sub-networks, integrate the modularity in each sub-network, and optimize the composite modularity based on Louvain algorithm to achieve community detection. The algorithm does not require prior knowledge, and is suitable for large-scale networks and general morphology networks.
Obviously, the extended modularity methods evolves from the algorithm in the homogeneous network, and has high stability. However, the method has high time complexity and cannot avoid the limitation of maximum modularity resolution, which makes it impossible to detect the small communities in the large-scale network (Fortunato, 2009; Lancichinetti et al., 2011; Fortunato and Barthélemy, 2007).
Homogeneous methods of heterogeneous networks methods
Since the community detection method of homogeneous networks is relatively mature, the dimensionality of heterogeneous networks can be reduced into homogeneous networks, and then homogeneous network community detection method can be used for it. The dimension-reduction methods of heterogeneous networks mainly include non-negative matrix factorization (NMF) (Lee et al., 1999), topic model (Blei et al., 2003), principal component analysis (PCA) (Jolliffe, 2002), linear discriminant analysis (LDA) (Scholkopft and Mullert, 1999), among other.
Non-negative matrix factorization methods
Non-negative matrix decomposition methods can decompose any given non-negative matrix into two non-negative matrices (Liu et al., 2016), which are the basis matrix and the coefficient matrix respectively. The coefficient matrix is used to replace the original matrix to achieve dimensionality reduction. Tafavogh proposed a heterogeneous network community detection method based on matrix decomposition and semantic paths (Tafavogh, 2014). Zhang proposed a non-negative matrix three-factor decomposition method, HMFClus, which calculates similarity and integrates the information between objects of the same type into HMFClus. This method can simultaneously cluster all types of objects in a hybrid network (Zhang et al., 2016). Liu et al. proposed a penalized alternating factorization (PAF) algorithm to solve the corresponding optimization problems from the perspective of matrix decomposition for multi-layer attribute network. PAF algorithm not only has good effect on community detection, but also has strong applicability to network morphology (Liu et al., 2020).
Topic model methods
The introduction of topic model can excavate the hidden topic information in text information, so as to improve the effect of community detection. Mei et al. (2008) combined topic model with social network analysis, made full use of the advantages of statistical topic model and discrete regularization, improved topic model through regularization, and realized community detection.
Principal component analysis (PCA) methods and linear discriminant analysis (LDA) methods
Both of these two methods are linear dimensionality reduction methods, and use linear projection methods to map high-dimensional data to low-dimensional space. The difference between the two methods lies in that the former ensures that the data after dimensionality reduction retains more original information, while the latter makes the data after dimensionality reduction easier to distinguish. Existing studies only apply these two methods in single-node type networks (Lin et al., 2014; Li et al., 2016; Yuan et al., 2016) or bipartite networks (Liu and Chen, 2013).
It can be seen that although homogeneous methods of heterogeneous networks methods are easy to understand, the process of dimension reduction of heterogeneous networks into homogeneous networks is complicated, which is easy to cause information distortion, and the implementation complexity is too high. Because some methods need to estimate the number of communities, this method cannot meet the community detection requirements of large-scale networks.
To sum up, the existing community detection methods of hybrid networks with multi-node and multi-relationship are mostly based on probabilistic model and meta-paths, while the methods based on seed nodes, extended modularity and homogeneous methods of heterogeneous networks are still in the exploratory stage. In addition, there are still many problems to be solved in various methods, which indicates that there is still a lot of room for further research on community detection methods of multi-node and multi-relationship hybrid networks.
Commonly used evaluation indicators of community detection effect
There are many kinds of evaluation indicators for the effect of community detection, and different evaluation indicators are used for different community detection methods and different experimental needs. Three commonly used indicators are mainly introduced here: Normalized Mutual Information (NMI) (Lancichinetti et al., 2009), Adjusted Rand Index(ARI) (Santos and Embrechts, 2009), and Modularity Q (Newman and Girvan, 2004). Among them, NMI and ARI are evaluation indicators for known real community detection results, while Modularity Q is for unknown.
Normalized Mutual Information (NMI) is a similarity measurement method based on information theory and probability theory to evaluate community detection results. It is usually used to detect the difference between real detection results and actual detection results, which can intuitively show the quality of community detection results. The NMI calculation formula is as follows:
A and B are the result sets divided from the network, N is the number of all nodes, CA and CB represent the number of communities in A and B respectively, Cij represents the number of nodes shared by the two communities, and Ci (Cj) is the sum of the elements in row i(j) in C. The value range of NMI is [0,1], and the larger the value is, the more accurate the result is.
In a broad sense, ARI measures the coincidence degree of two data distributions, that is, the similarity between real detection results and actual detection results is compared through whether each point pair is consistent under different community detection, which is defined as follows:
Among them, a11 represents the number of point pairs that belong to the same community in the real community and the actual community , a00 represents the number of point pairs that do not belong to the same community in the real community and the actual community, a10 represents the number of point pairs that belong to the same community in the real community but not belong to the same in the actual community, a01 represents the number of point pairs that do not belong to the same community in the real community but belong to the same in the actual community. The value range is [-1,1]. The larger the value is, the more consistent the actual result is with the real result. Compared with NMI, ARI has a higher degree of discrimination.
The modularity function Q was proposed by Newman and Girvan (2004). By optimizing the modularity Q, a better community division result can be obtained. The modularity Q can make the nodes within the community more closely connected, so it is an indicator to measure the strength of the community, which is defined as follows:
Among them, i and j are any two nodes, ki and kj are the degrees of nodes i and j respectively, and m is the total number of edges in the network. When two nodes are directly connected, Aij=1, otherwise it is 0; Ci and Cj are the communities to which nodes i and j belong respectively. If the two nodes belong to the same community, it is =1, otherwise it is 0. The value range is [0,1]. The larger the Q value, the more stable the community detection structure is and the better the effect is.
Examples of papers on the community detection in hybrid network
In this section we present relevant studies about the community detection, particularly in academic networks. One of the relevant a complete publication we have found is the book edited by Wasserman S, Galaskiewicz J. (Wasserman and Galaskiewicz, 1994). The book shows how social network analysis has been used to advance substantive research in the social and behavioral sciences. The editor introduced researches in several topics from the social psychology and diffusion research, to anthropology and communications, and to politics and organization studies, span the range of social network analysis applications. From the theoretical and basic point of view we highlight the delightful paper of Fortunato (Fortunato, 2010). Here, the author presents a thorough exposition of the topic, from the definition of the main elements of the problem, to the presentation of most methods developed, with a special focus on techniques designed by statistical physicists (as the Pott technique), from the discussion of crucial issues like the significance of clustering and how methods should be tested and compared against each other, to the description of applications to real network. Other basic research was the paper of Newman (Newman et al, 2004). They proposed a set of algorithms for discovering community structure in networks-natural divisions of network nodes into densely connected subgroups. In (Van den Besselaar and Heimeriks, 2006) introduced a method to a method in which title words are used as indicators for the content of a research topic, and cited references are used as the context in which words get their meaning. In that paper, research topics were represented by sets of papers that are similar in terms of these word-reference combinations.
Community detection in the more specific field of the professional network was studied by Suthers et al (Suthers et al., 2013). Also, interesting approximations on heterogeneous networks using a combination of techniques can be found in (Sun et al, 2009; Tang and Liu, 2010; Ji et al, 2011). Application of evolutionary clustering for analysis of bibliographic networks was reported by (Gupta et al., 2011). A relevant study using spectral clustering for heterogeneous networks was reported by Sengupta and Chen (Sengupta and Chen, 2015). On the other hand, Sun et al. (Sun et al, 2013) integrated meta-path selection with user-guided clustering to cluster objects in networks to generate clusters under the learned weights of meta-paths. Using Principal Component Analysis (Jolliffe, 2002) has been used to perform community detection in disease-gene network (Liu and Chen, 2013). A very interesting contribution in multiplex networks using a seed-centric approach was reported by (Hmimida, Kanawati, 2015)
More recently, the book “Heterogeneous Information Network Analysis and Applications” provides a comprehensive survey of current developments of heterogeneous information network. It also presents the newest research in applications of heterogeneous information networks to similarity search, ranking, clustering and recommendation (Shi and Yu, 2017). A very complete survey about this topic, including concept, techniques, algorithms and data was published by (Khan and Niazi, 2017). Also, the survey of heterogeneous information network analysis by (Chuang et al., 2017) introduce basic concepts of heterogeneous information network analysis, examine its developments on different data mining tasks, discuss some advanced topics, and point out some future research directions.
Recent developments
In the community detection field, new topics and techniques are emerging every day. Based on the extracted (Wang and Han, 2021) developed a novel attractive research community ranking (ARTRank) algorithm to rank the research communities. They are interested to answer the question: which is the most attractive research community in the academic social network? The main idea of the proposed algorithm lies in two measurements for each community: a positiveness score and a negativeness score, which measure the attractiveness of a community from the in-attention aspect and the out-attention aspect, respectively. New metrics as the collaboration score, to quantify the collaboration between collaborators, are introduced (Dilmaghani et al., 2019). Extensions of the meta-path approach with has new similarity measures been recently used to study heterogeneous information networks (Wang et al, 2020). Also, a model based on the community detection method allows to detect topic-oriented densely-connected communities in which community members have active interactions among each other (Das and Anwar, 2019). On the other hand, (Liu et al., 2020) studied the integrative community detection problem of a multi-layer attributed network from the perspective of matrix factorization. Authors proposed a penalized alternative factorization (PAF) algorithm to resolve the corresponding optimization problem, followed by the convergence analysis of the PAF algorithm. A new multiplex network embedding model with high-order node dependence has been recently developed estimate the local structural complementarity of nodes as an embedding constraint of interlayer dependence (Ning et al, 2021). At present, meta-graph is one of the most powerful tools for similarity search on heterogeneous information networks (meta-graph is a composition of meta-paths that captures the complex structural information). In this sense, some interesting developments including embedded meta-paths information have recently reported (Sun, L. et al., 2018). The use of deep learning techniques has been in the focus in recent years. Particularly, unsupervised deep learning models (e.g. stack autoencoders) have been successfully proposed for the problem of community detection, which can extract network features and use them in splitting the network into communities (Pinaya et al., 2020; Al‑Andoli et al., 2020)). A survey about this topic has been published recently (Al‑Andoli, 2021)
Finally, a novel community detection method based on the similarity of communication behavior between IP nodes allowed the accurate detection and analysis of the community structure in large-scale IP networks could be highly beneficial for their optimization and security management (Zhang, et al, 2020).
CONCLUSIONS
We present a revision about the methods of community detection in hybrid network, and its application to the network analysis. Both the main techniques and the methods used for community detection were presented. Also, a short description of the general features of this field was introduced. Traditional Community Detection Techniques, Modularity Optimization Based Community Detection Techniques, overlapping community detection techniques and Dynamic Community Detection Algorithms were described. Examples of application of these techniques were presented. Finally, relevant examples of the community detection in hybrid network applied to network analysis and recent developments in this field were discussed. Considering the revised literature, we propose a hybrid network community detection algorithm based on meta-path, seed nodes and extend modularity method to study the academic networks. Our idea is to construct a hybrid network community detection method with strong network applicability, low complexity, and the ability to combine network topology and text information simultaneously.