INTRODUCCIÓN
Las organizaciones buscan constantemente mejorar el control de la gestión de sus procesos, asignando recursos y conocimientos para alcanzar sus objetivos estratégicos dentro de la misión y visión que poseen, mediante un proceso de toma de decisiones adecuado.
Sin embargo, no todas las organizaciones logran tener éxito en esa búsqueda. Según Retiz (2018), existen deficiencias en los sistemas de control de gestión actuales, tanto a nivel operativo como estratégico. A partir de las deficiencias encontradas se plantea la necesidad de reconsiderar las concepciones del control y su aplicación eficaz.
Por lo tanto, es crucial orientar el control de la gestión hacia las estrategias, la estructura organizativa, así como fortalecer los sistemas de información con datos cualitativos y cuantitativos. Esto debe permitir la retroalimentación y la proyección proactiva basada en la información recopilada, para facilitar la toma de decisiones efectivas.
La finalidad primordial de establecer un adecuado control de gestión, es que la gerencia disponga de una herramienta operacional y proactiva de fácil acceso que facilite su incidencia, a través de la toma de decisiones, en el control de los gastos incurridos, por tanto de los costos en general de la organización, con el objetivo de obtener producciones de calidad con el mínimo de erogaciones posibles, en busca de mayores rendimientos productivos y financieros, con mayor competitividad en el mercado; los que deben constituir elementos culmen de cualquier estrategia empresarial.
Para que los costos sean una herramienta efectiva en la superación de obstáculos durante los procesos organizacionales, es esencial que se gestionen y controlen de manera adecuada. Como señala Lomelí (2018), es fundamental tener una comprensión precisa de los costos en cualquier entidad, ya que una gestión deficiente de los mismos puede tener consecuencias significativamente negativas. Por lo tanto, las industrias necesitan actualizar sus modelos de control de costos, como una estrategia para abordar estos desafíos y asegurar la administración eficiente de sus recursos disponibles.
Dentro de la gestión y control de costos en las organizaciones, existe una variedad de sistemas de acumulación, métodos y herramientas, siendo el costo estándar uno de los más destacados. Estos costos están diseñados para cumplir con las necesidades de planificación, organización, dirección y control en la toma de decisiones, mediante la predefinición de costos a través de métodos científicos.
Los costos estándar contribuyen a garantizar que las actividades productivas se desarrollen de acuerdo con las pautas establecidas y con eficiencia. Esto se logra mediante el análisis de las variaciones entre los costos reales de la empresa y los costos estándar, previamente establecidos para sus actividades o productos.
En Cuba, se reconoce la importancia de los costos estándar en la valoración de los costos de producción y servicios. Esto se refleja en la Norma específica de Contabilidad núm. 12, emitida por el Ministerio de Finanzas y Precios (MFP) en 2018, la cual presenta técnicas fundamentadas en el uso de Costos Predeterminados (MFP, 2018). En esta norma, se hace hincapié en la utilización de los costos estándar como una herramienta avanzada para el control de los mismos, destacándolos entre las técnicas basadas en costos predeterminados.
Según lo indicado por el MFP (2018), los costos estándar permiten realizar cálculos de eficiencia de manera rigurosa al basarse en normas y regulaciones científicamente fundamentadas, para evaluar materias primas, materiales y costos indirectos involucrados en el proceso de producción.
Los renglones económicos exportables de la actividad industrial en Cuba, además de la incertidumbre propia del mercado internacional, enfrentan un entorno altamente competitivo, con grandes limitaciones tecnológicas y de la economía nacional. La reducción de los costos productivos y el perfeccionamiento de su control, resultan indispensables en tales escenarios.
La industria siderúrgica cubana, en particular, asume mayores desafíos debido a la crisis internacional del sector, provocada por la desaceleración económica de naciones líderes en la producción de acero (Hossain, 2023).
Otro elemento a considerar es el aumento de los precios, en los mercados internacionales, de las principales materias primas necesarias para la producción de aceros. En el caso específico de las chatarras, estas sufren las variaciones de precio inherentes a su naturaleza económica de commoditie y a la globalización de una red comercial de metales de desechos, de escala libre y con una clara tendencia a la monopolización (Hu, Wang, Lim & Koh, 2020). Lo que genera mayores retos al control de los costos productivos del acero en Cuba y evidencia la necesidad de introducir nuevos instrumentos para sustentar los procesos de toma de decisiones asociados.
Todo lo anterior justifica que el objetivo general de esta investigación sea, diseñar un modelo de optimización de los costos de material directo en la elaboración de aceros al carbono, que permita sustentar matemáticamente la toma de decisiones respecto a la composición de las coladas y el requerimiento de materiales.
DESARROLLO
Los modelos matemáticos, el control de gestión y la toma de decisiones
Las organizaciones se encuentran en una búsqueda continua para mejorar el control de la gestión de sus procesos. Con tal fin se movilizan esfuerzos, recursos y conocimientos, en aras de lograr los objetivos estratégicos trazados, en el marco de la misión y visión organizacional, mediante un adecuado proceso de toma de decisiones.
No es tarea sencilla diseñar e implementar exitosamente en una organización un sistema de control de gestión, pues este tiene que responder a las características y particularidades de la empresa, e incluso de cada uno de sus procesos y actividades, para que realmente juegue el rol y encargo que desde el punto de vista operativo y estratégico la gerencia requiere y necesita para su uso eficaz. Es allí donde estudiosos y expertos del tema señalan sus mayores debilidades, deficiencias y carencias.
Lo anterior presupone la realización de un estudio pormenorizado de las actividades y procesos que efectúa la empresa, así como de un diagnóstico que levante desde sus diferentes áreas funcionales, con mayor fuerza en el caso de las productivas, los requerimientos de información cualitativa y cuantitativa de forma tal que logre enfocar el control de gestión hacia las estrategias y la estructura de la organización. Esto deberá aplicarse de manera que permita tanto la retroalimentación, como la proyección proactiva a partir de la información recopilada, para una toma de decisiones efectiva.
Mediante el control de gestión, se busca influir en resultados futuros de manera que aumente la probabilidad de que estos ocurran y tengan un comportamiento positivo, dicho de otra manera, el control de gestión es un sistema de dirección con el que se pretende impactar en el futuro de la organización en lugar de solo controlar su pasado.
La actividad industrial en Cuba, en los actuales entornos competitivos a los que se enfrentan sus producciones exportables, junto a la necesidad de responder de forma adecuada a los continuos cambios y constante incertidumbre que se generan en el mercado internacional, demanda una significativa modificación en lo que a la gestión empresarial se refiere. El control de gestión, como proceso vinculado a la toma de decisiones de la dirección empresarial, resulta esencial para tales propósitos, pues contribuye a mejorar la actuación de cualquier sistema productivo.
En el contexto cubano, la concepción del control de gestión influye en los nuevos enfoques gerenciales que asumen las empresas organizadas a partir de la gestión integrada. El clima competitivo del país se multiplica ante la dinámica del cambio, la apertura de la economía y la presencia de ciclos de negocios cada vez más cortos.
Esto plantea un reto para las empresas, tanto productivas como de servicios, por la necesidad de lograr y mantener determinados niveles de competitividad, así como alcanzar mejores resultados en su gestión.
El control de gestión como función especializada en lo económico, no puede encerrarse en las cuentas del plan contable; sino que es necesario que abarque todos los procesos y actividades. A la par, la eficiencia económica no puede obtenerse después de la acción, tiene que crearse antes; desde una planificación acertada, seguida de una ejecución eficiente y acompañada de un control permanente.
Esto deriva, a su vez, en la implementación de medidas oportunas para el establecimiento de una mejora continua. Por tanto, el control debe ser diseñado de acuerdo con las estrategias, objetivos y planes existentes.
Afirma Álvarez, Zaldívar, Moreira, Giler y Bonin (2020) que, en este contexto, resulta necesario el uso de modelos de control articulados con iniciativas y esfuerzos individuales, consistentes con las relaciones entre planificación y control.
En la contabilidad de gestión moderna, Hernández-Madrigal (2020) identifica el perfeccionamiento e introducción de sistemas y métodos de apoyo al análisis de los costos y la toma de decisiones, entre los que se señalan: los costos estándar y los métodos de investigación de operaciones.
En el ámbito de la aplicación de los costos estándar, es significativo el aporte de los modelos matemáticos a la toma de decisiones, a partir del desarrollo de la Investigación de Operaciones y sus modelos de optimización, como se puede apreciar en los trabajos de Alzate, 2016; Avenali, Boitani, Catalano, D’Alfonso y Matteucci, 2018; Nishimura, 2019; Tsai, Lan y Lee, 2020; Zhao, Grossmann y Tang, 2018.
Plantean Caicedo, Criado y Morales (2019), que la utilización de los modelos de optimización, contribuye a la reducción de los costos y al uso eficiente de los recursos, lo cual le confiere una mayor relevancia dentro de la comunidad científica internacional. Así mismo, Cevallos-Bravo (2021) afirma que, la implementación de sistemas con enfoque a la optimización en la gestión de costos, es fundamental para la implementación de las estrategias en el entorno empresarial actual y cada vez más necesario para las industrias a nivel mundial.
La industria siderúrgica y los modelos matemáticos de programación lineal
Uno de los modelos de optimización de mayor alcance y aplicación en la industria siderúrgica, es el Modelo general de programación lineal. Acerca de este modelo, Hillier y Lieberman (2021), afirman que “…el desarrollo de la programación lineal ha sido calificado como uno de los avances científicos más importantes de mediados del siglo XX” (p. 25). Según estos autores, este modelo se aplica al problema general de asignar, de manera óptima, recursos limitados, mediante la determinación del nivel de ciertas actividades que compiten entre sí, por estos recursos.
El marco de aplicación de la programación lineal a la industria siderúrgica alcanza, entre otras: la localización de instalaciones de producción, la selección de clientes y proveedores, la optimización logística, optimización de redes y la minimización de costos productivos, energéticos y ambientales.
Existen varios tipos de modelos especiales derivados del modelo general, entre los que se pueden mencionar los problemas de transporte, asignación y mezcla. Para los modelos de mezcla, se utiliza generalmente una función objetivo de minimización de costos y se incluyen restricciones de composición, además de las restricciones funcionales del proceso productivo que se desea optimizar.
Este tipo de modelo resulta útil para la optimización de la producción de acero, el cual se obtiene a partir de la fundición de una mezcla de materiales (chatarras, ferroaleaciones, material de carga, entre otros) y debe cumplir con requerimientos de composición química específicos por marca (Das & Ghosh, 2023).
Entre los modelos de optimización para la producción de acero registrados en la bibliografía, destacan algunos debido a su alcance y efectividad demostrada en la estandarización y reducción de costos productivos en la siderurgia.
El modelo de programación lineal entera mixta, formulado por Zhao et al. (2018), para la optimización del costo asociado al consumo energético del subproceso de laminación en la producción de perfiles y barras de acero, incluyó la consideración de la demanda y la optimización del consumo de energía bajo tarifas de electricidad en función del tiempo de uso.
El objetivo principal fue coordinar la producción y el consumo de electricidad para minimizar los costos de producción típicos en las secciones intensivas en energía de la industria del acero. Los resultados numéricos demostraron la eficiencia y solidez del modelo y se sugirió que este enfoque podría extenderse a otras industrias con estructuras similares de producción en múltiples etapas.
Para optimizar el proceso de desoxidación y aleación en la producción de acero (Zhao, Shijie Li, & Shuaikang Li, 2020), se utiliza un análisis de regresión de componentes principales para reducir la dimensionalidad de los factores influyentes y se establece un modelo de predicción confiable de rendimiento de elementos. Luego, se aplicó la programación lineal para diseñar un plan de mezcla de menor costo que cumpla con los estándares nacionales y los requisitos de producción. Los resultados proporcionaron un modelo de optimización confiable para el proceso de desoxidación y aleación en las acerías, que mejoró la competitividad en el mercado, pues permitió reducir los costos productivos y la generación de desechos.
Con el objetivo de estabilizar la red eléctrica mediante la producción de acero en momentos de menor demanda y aprovechar las variaciones en los precios de la electricidad, Castro, Dalle Ave, Engell, Grossmann y Harjunkoski (2020) abordan la gestión de la demanda energética industrial en una planta siderúrgica, mediante un modelo de programación lineal entera mixta (MILP).
Para la modelación, se tuvo en cuenta la eficiencia energética, la duración de las tareas de fusión y la degradación de los electrodos. Los resultados del estudio indicaron que se logró evitar el modo de alta potencia, además de permitir una ejecución más rápida en momentos de precios bajos de la electricidad. Esto destacó la importancia de la aplicación de la programación lineal en la planificación de la sustitución de electrodos y su efecto en la minimización de costos productivos totales.
En su investigación, Rosyidi, Hapsari y Jauhari (2021) desarrollan un modelo de planificación de producción integrado para una gran empresa de fabricación de acero. El objetivo fue maximizar la ganancia total a partir de restricciones como el programa de mantenimiento, la tasa de defectos, el inventario, la capacidad de cada unidad, y otros factores. El modelo de programación lineal generó una ganancia total equivalente a más de 283 millones de dólares estadounidenses (IDR 4.352.726.438.000,00).
Los resultados del análisis de sensibilidad mostraron que la función objetivo era sensible a cambios en el costo de mantenimiento, el precio de la materia prima y el precio de venta del producto. Los autores sugirieron que la empresa implementase la planificación de producción integrada para maximizar las ganancias e investigara la incertidumbre en aspectos como la demanda y la calidad de los productos intermedios y finales.
Para abordar el problema de corte de una dimensión (1D-CSP) en la industria del acero, Morillo-Torres et al. (2021), presentan un modelo de programación lineal entera mixta (MILP, por sus siglas en inglés). Se utiliza un estudio de caso en una empresa metalúrgica con el objetivo de minimizar el desperdicio en el proceso de corte de barras de acero, a partir de restricciones de inventario y del uso potencial de los remanentes resultantes.
Los resultados computacionales mostraron una solución óptima con una mejora promedio en la reducción de desperdicio del 80 %. No se encontraron diferencias significativas al comparar los resultados entre el modelo completo y el modelo sin restricciones de inventario. Este enfoque tiene aplicaciones industriales en la optimización de procesos de corte de barras de acero para la reducción de costos productivos.
En el estudio realizado por Zhou et al. (2022), se buscó optimizar la proporción de mineral de hierro en el proceso de sinterización para reducir costos sin comprometer la calidad. Mediante la programación lineal, se evaluaron las propiedades de siete tipos de minerales de hierro y se establecieron restricciones basadas en datos de una planta de sinterización.
El modelo optimizado resultó en una proporción específica de minerales que redujo los costos de mezcla en aproximadamente 12 CNY/ (t-mineral mezclado). Las pruebas de sinterización confirmaron que esta optimización apenas afectaba el rendimiento, lo que demuestra que, la programación lineal puede reducir significativamente los costos de mineral de hierro en el proceso de sinterización sin comprometer la calidad del producto.
Para optimizar la secuenciación y reducir el desperdicio en el proceso de corte de barras de acero, Figueredo-Tran et al. (2022), utilizaron dos enfoques principales: la Programación Lineal (PL) y la Modelización y Simulación para la gestión estratégica de la producción. Desarrollaron un modelo matemático de Programación Lineal para secuenciar la producción y minimizar los retrasos. Se emplearon parámetros, variables y restricciones para representar el proceso de producción y las capacidades de entrega.
La simulación de Redes de Petri se utiliza para identificar puntos de mejora en la eficiencia de producción. Los resultados mostraron que el modelo de Programación Lineal eliminó los retrasos y entregó materiales por adelantado. La simulación de Redes de Petri identificó mejoras para una mayor eficiencia de producción. Este estudio demuestra la complementariedad de la Programación Lineal y la Modelización y Simulación en la resolución de problemas estratégicos en la industria del acero, proporcionando una visión integral de la gestión de procesos.
Los modelos estudiados, aunque constituyen evidencias de las ventajas de incorporar modelos de programación lineal a la optimización de costos en la producción de acero, fueron diseñados para plantas siderúrgicas con características que no aplican a las condiciones de la producción de acero en Cuba.
Modelo de programación lineal para optimizar costos en la siderúrgica cubana
La obsolescencia tecnológica, la ausencia del uso de mineral de hierro y de altos hornos; además de restricciones energéticas excepcionales, de disponibilidad de recursos y de acceso al mercado internacional de materias primas, afectan al sector nacional. Por lo tanto, se requiere del diseño de un modelo propio para la optimización de los costos productivos en la industria siderúrgica cubana.
A partir de los modelos estudiados, para dar cumplimiento al objetivo trazado en la presente investigación, se diseñó un modelo de programación lineal (tipo mezcla), para la optimización del costo de material directo en la producción de aceros en Cuba. El modelo se implementó en la Empresa de Aceros Inoxidables de Las Tunas (ACINOX), para realizar los ajustes necesarios y valorar su pertinencia. Esta empresa constituye la mayor exportadora de aceros bajo y medio carbono, dentro del sector siderúrgico cubano, en los últimos años.
En la empresa ACINOX, se desarrolla la producción de aceros, mediante la tecnología de Horno de Arco Eléctrico (HAE), con la cual se transforma la carga metálica (chatarra) en metal líquido, con una composición química previamente especificada. Para lo cual se realizan los siguientes subprocesos principales:
Metalurgia primaria (fusión), el cual tiene lugar en un horno de arco eléctrico de piquera, con una capacidad operativa de 60 t y electrodos de 500 mm de diámetro para la generación del arco. Además de la fusión de la carga (chatarra), se realiza un ajuste primario del acero.
Metalurgia secundaria (ajuste y afino), se realiza en un Horno Cuchara (HC), tipo LF5060, con una capacidad de 60 t, en el que se utilizan electrodos de 300 mm. En este subproceso se obtiene la marca de acero especificada.
Vaciado, tiene lugar en la Instalación de Vaciado Continuo (IVC), agregado metalúrgico donde se lleva a cabo la transformación del acero líquido procedentes de la elaboración y afino, a palanquillas sólidas de diferentes medidas.
También deben mencionarse los talleres de producto terminado, en que se recepciona, organiza y controla la producción terminada; el taller de reverbería, encargado de brindar servicios de reparación y montaje de refractarios; la existencia de un grupo de plantas auxiliares y una subestación eléctrica. Esta última juega un rol decisivo, debido a los altos consumos de energía, propios del proceso productivo. Para esto cuenta con un sistema capaz de recepcionar y distribuir la energía eléctrica a cada uno de los talleres y plantas.
A partir de los datos económicos de la industria, planes productivos, fichas de costo y estimaciones de indicadores técnico-energéticos, se determinó el peso de los diferentes elementos de material directo, que intervienen en la formación del costo de producción.
Se decidió incluir en el modelo solo aquellos recursos que se pueden optimizar y que representan alrededor del 80 % de los costos directos de producción de acero líquido. Estos se listan a continuación:
1 Chatarra Ferrosa (t)
2 Chatarra Importada (t)
3 Chatarra desmantelamiento (t)
4 Recirculación (t)
5 Hierro Fundido (t)
6 Ferro Sílico Manganeso (t)
7 Ferro Silicio (t)
8 Carbón de Carga (t)
9 Carbón de Insuflado y Reducción (t)
10 Carbón Ajuste (t)
11 Sidox/Lugited Al (t)
12 CaF2 (t)
13 300 mm (t)
14 500 mm (t)
15 O2 (Nm3)
16 Electricidad Horno de Arco Eléctrico (MWh)
17 Electricidad Horno Cuchara (MWh)
18 Cal (t)
El número a la izquierda de cada recurso constituye el índice que se utilizará para referirse al mismo en la definición de las variables del modelo. De donde se declara:
Variables de decisión
Xij: cantidad de recurso j a utilizar en la producción del acero marca i
Función objetivo
Donde m: cantidad de marcas de acero a planificar; Cj: Costo unitario del recurso j.
Mediante análisis documental y consulta a especialistas, se identificaron como principales elementos restrictivos los que a continuación se muestran:
1. Disponibilidad de recursos
2. Productivas y de rendimiento
3. Composición química según parámetros de calidad
4. Composición de residuales
5. Relaciones de consumo
6. Restricciones técnicas y energéticas
Por lo que se declara el siguiente sistema de restricciones funcionales a las que está sujeta la función objetivo, en el que se presenta solo un extracto representativo del centenar de restricciones modeladas.
1. Rendimiento
Donde rj: Índice de rendimiento de la materia prima j; Pj: Plan de producción del acero marca i.
2. Disponibilidad de recursos
Donde Dj: Disponibilidad del recurso j.
3. Limitación del uso de Hierro fundido (limitación técnica)
4. Limitación del contenido Fe
Donde CFej: Índice de contenido de hierro en la materia prima j.
Requerimientos de marca
5. Requerimiento mínimo de contenido de carbono (C)
Donde CCj: Índice de contenido de carbón en el recurso j; CMinCi: Contenido mínimo de carbón requerido en el acero marca i.
6. Limitación del contenido de carbono (C)
Donde CMaxCi: contenido máximo admisible de carbono en el acero marca i
7. Limitación del contenido de Fósforo (P)
Donde CPj: Índice de contenido de fósforo; CMaxPi: Contenido máximo de fósforo en el acero marca i
8. Limitación del contenido de Azufre(S)
Donde CSj: Índice de contenido de azufre; CMaxSi: Contenido máximo de azufre en el acero marca i.
9. Limitación del contenido de Cr+Ni+Cu
Donde CMaxCrNiCui: Contenido máximo de cromo, niquel y cobre en el acero marca i.
10. Limitación del contenido de Cr+Ni+Cu+Sn
Donde CmaxCrNiCuSni: Contenido máximo de cromo, niquel, cobre y estaño en el acero marca i.
11. Relación Oxígeno-Carbono (requisito técnico)
12. Requerimiento energético en el HAE
Donde Iej: Índice energético de la chatarra j (MWh/t); Rej: Rendimiento energético de la chatarra j (%); Xi15: Consumo de oxígeno en la producción del acerco marca i; Xi16: Consumo eléctrico en el HAE en la producción del acerco marca i
13. Requerimiento energético en el HC
Condición de no negatividad
Recopilación y tratamiento de la información
Para la estimación de los coeficientes del modelo, se utilizaron las bases de datos del grupo técnico y el departamento contable, correspondientes al periodo comprendido entre enero 2019 y diciembre 2021. Se utilizaron estimaciones de costos y precios de compra a partir de los reales observados por cada elemento en las fichas de costo.
La estimación puntual de las medias poblacionales, se realizó a partir del cálculo de medias muestrales acotadas. Para esto se utilizaron los valores muestrales que se ubican entre los percentiles 5 y 95, con el objetivo de eliminar las observaciones derivadas de situaciones irregulares o atípicas, que constituyen valores extremos y pueden sesgar la estimación puntual de los promedios y sus desviaciones.
El modelo descrito fue transformado en ecuaciones según la sintaxis de Microsoft Excel para su implementación y solución mediante su herramienta complementaria. Esta resulta eficiente para realizar los cálculos necesarios pues, como afirma Majumdar (2022), “…Microsoft Excel encapsula todas las matemáticas que hay detrás de la resolución de problemas de programación lineal en su herramienta complementaria llamada Solver” (p. 116).
El libro Excel resultante, fue concebido de manera que el usuario pueda introducir los parámetros necesarios para la producción de cualquier marca de acero, con sus coeficientes específicos. El mismo se compone de tres hojas de cálculo fundamentales; Hoja Entrada de datos, Hoja Solver y Hoja Reporte; las cuales se describen a continuación.
Hoja entrada de datos
El planificador puede introducir los valores requeridos en la hoja de entrada de datos de manera organizada y sencilla (Fig.1). La hoja tiene implementadas reglas de validación con el objetivo de reducir los errores humanos asociados a este proceso.
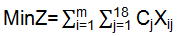 Fuente: Elaboración propia (hoja de cálculo en Libro Excel utilizando la herramienta Solver)
Fuente: Elaboración propia (hoja de cálculo en Libro Excel utilizando la herramienta Solver)Fig.1 Hoja entrada de datos
Los datos incluyen los valores de los planes de producción de acero líquido por marca de acero y sus especificaciones relacionadas con su composición química. En cuanto a los recursos deberá introducir los valores relacionados con los precios, las disponibilidades o existencias, los rendimientos productivos y energéticos; composición química; elementos restrictivos e índices energéticos. El botón resolver, permite realizar los cálculos para la solución del modelo.
Hoja Solver
Esta hoja contiene todas las variables y ecuaciones del modelo; función objetivo y restricciones (Fig. 2). La misma se actualizará automáticamente a partir de los datos introducidos en la hoja de entrada, por lo que el usuario solo requiere acceder a la hoja Solver, para realizar actualizaciones al modelo.
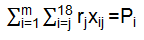 Fuente: Elaboración propia (hoja de cálculo en Libro Excel utilizando la herramienta Solver)
Fuente: Elaboración propia (hoja de cálculo en Libro Excel utilizando la herramienta Solver)Fig.2. Hoja Solver
En esta aparecerán las soluciones del modelo de programación lineal pero expresadas según el formato matemático del mismo.
Hoja Reporte
En la hoja reporte, se muestran automáticamente las salidas o soluciones obtenidas en un formato acorde con los modelos de reporte implementados en ACINOX (Fig.3). El usuario puede consultar los consumos por recurso para cada marca de acero, los subtotales, totales e índices de consumo esperados según la planificación aportada.
Igualmente muestra los costos totales y específicos por marca de acero y el costo unitario por tonelada total. El botón imprimir reporte, genera un archivo PDF (Formato de documento portátil) con la tabla resultante.
Validación del modelo
Para la validación del modelo, se procedió a identificar los ocho meses de mayor estabilidad productiva en lo referido a disponibilidad tecnológica, energética y de materias primas. Bajo las condiciones reales y los pedidos producidos en cada uno de estos períodos, se aplicó el modelo propuesto para comparar los valores modelados con los reales observados.
Es importante destacar que los valores de los índices de consumo de los conceptos genéricos de costo de materiales modelados (chatarra, ferroaleaciones y material de carga), no difieren significativamente de los valores técnicos establecidos en ACINOX. Una vez comprobado el supuesto de normalidad para cada uno de estos conceptos, mediante la prueba no paramétrica de Kolmogorov-Smirnov (con valores de significatividad superiores a 0,12 en los tres casos); la prueba T-Student de diferencia de medias, se aplicó con resultados favorables a la igualdad entre los valores medios teóricos y los modelados, con significatividades respectivas de 0,07; 0,12 y 0.06 para las chatarras, las ferroaleaciones y el material de carga. En todas las pruebas se asumió un nivel de significación de 0,05.
El análisis comparativo relacionado con los costos de material directo de producción, permitió evidenciar una reducción significativa en los conceptos de chatarras, consumo eléctrico y, en consecuencia, en el costo total de material directo; toda vez que el consumo eléctrico y de chatarras, constituyen más del 60% de los costos productivos de material directo. En la Tabla 1 se muestran las reducciones porcentuales del costo para cada uno de los 8 meses comparados.
Tabla 1 Disminución porcentual de los costos mensuales (%)
| CONCEPTO | mes 1 | mes 2 | mes 3 | mes 4 | mes 5 | mes 6 | mes 7 | mes 8 |
| Chatarras | 10.5 | 7.5 | 2.9 | 4.4 | 7.4 | 5.4 | 9.8 | 12.1 |
| Electricidad HAE | 14.6 | 12.4 | 9.9 | 11.4 | 12.3 | 11.7 | 13.1 | 13.1 |
| Electricidad HC | 19.8 | 16.8 | 14.4 | 20.5 | 16.0 | 20.1 | 19.5 | 19.1 |
| Electricidad Total | 14.7 | 12.5 | 10.2 | 13.0 | 12.2 | 13.1 | 13.7 | 13.6 |
| COSTO DIRECTO ACERO LÍQUIDO | 13.93 | 10.59 | 15.15 | 14.94 | 10.39 | 12.37 | 18.62 | 12.69 |
Fuente: Elaboración propia a partir de los resultados obtenidos en la investigación.
Aunque los índices de consumo modelados de las chatarras no difieren significativamente de los consumos históricos, el costo unitario se ve reducido debido a la combinación óptima de los diferentes tipos de chatarras que aporta el modelo, para la producción mensual de las diferentes marcas. Se aprecia una posible reducción mínima del 2,9 %, aunque en 5 de los meses comparados se registran ahorros superiores al 7,3 %.
Las disminuciones porcentuales del costo de electricidad alcanzan sus mayores cifras para el caso del consumo en el HC, con valores superiores al 14 %. Sin embargo, en términos del impacto en el costo directo total, la disminución del costo de electricidad en el HAE (de más del 10 % en los meses comparados), tienen una mayor relevancia, ya que el consumo energético de la siderurgia primaria, equivale a seis veces el consumo eléctrico del ajuste y afino, según el comportamiento de los datos mensuales del periodo enero 2019-diciembre 2021.
A pesar de que los resultados del modelo sugieren un incremento en el costo unitario del material de carga y el oxígeno, esto no afecta la disminución del costo directo total, debido al bajo peso de estos conceptos en la formación del costo de material directo. De ahí que se observen costos directos totales modelados, inferiores a los observados en la producción. Para todos los meses comparados, el modelo ofrece costos directos inferiores en más de un 10 % a los reales. Para tres de los meses, esta reducción del costo alcanza valores superiores al 14,9 %.
CONCLUSIONES
La reducción de los costos productivos es una de las metas permanentes en la industria siderúrgica, dado el entorno internacional altamente competitivo del sector. Debido a la complejidad del proceso productivo del acero, muchos investigadores recurren a la modelación matemática para hacer frente al reto de la minimización de los costos de material directo, asociados a la producción de este renglón económico.
El modelo de programación lineal diseñado, aporta una estructura adecuada para el tratamiento matemático de las variables, parámetros y elementos restrictivos asociados a la optimización de los costos de material directo en la producción de aceros.
Las pruebas comparativas realizadas, permiten verificar la pertinencia de la implementación del modelo propuesto, para la optimización de los costos productivos en la industria siderúrgica cubana; con especial impacto en la disminución de costos directos asociados al uso de las chatarras y al consumo eléctrico, los cuales representan más del 60 % del costo directo total.