Nuclear Sciences
β+ decay properties of A=100 isobars
Propiedades de la desintegración β+ de isóbaros con A = 100
Fatima Benrachi
1
*
, Nadjet Laouet
1
1Laboratoire Physique Mathématique et Subatomique, Université Frères Mentouri Constantine 1 (Algeria).
Abstract
The estimation of spectroscopic properties of neutron-deficient nuclei in the A=100 tin mass region is needed for the understanding of the rp-process path and the experimental exploration of the nuclear landscape. In order to evaluate some spectroscopic properties of the Gamow-Teller
β+
decay of neutron deficient isobars of A=100, we have performed shell model calculations by means of Oxbash nuclear structure code. The jj45pn valence space used consists of nine proton and neutron orbitals. The calculations included few valence hole-proton and particle-neutronin
π
g9/2 and vg7/2 orbitals respectively, in 100Sn doubly magic core. Effective interaction deduced from CD-Bonn one is introduced taking into account the nuclear monopole effect in this mass region. The results are then compared with the available experimental data.
Key words: nuclear structure; strontium 100; monopoles; 0 codes; beta-plus decay; neutron-deficient isotopes
Resumen
La estimación de las propiedadesespectroscópicas de los núcleosdeficientes en neutrones en la región de masas de estaño A = 100 es necesaria para la comprensióndelcaminodelproceso rp y la exploraciónexperimental de laestructura interna de los núcleos. Con el fin de evaluar algunas propiedades espectroscópicas de la desintegración
β
+de Gamow-Teller en los isótopos de estañodeficientes en neutrones con A = 100, hemosrealizadocálculosdelmodelo de capas mediante el código de estructuranuclear de Oxbash. El espacio de valencia jj45pn utilizado consiste en nueve orbitales de protones y neutrones. Los cálculosincluyeronpocoshueco-protóny partícula-neutrón de valencia en orbitales
π
g9/2 y vg7/2respectivamente, en un núcleo100Sn doblementemágico. La interacciónefectivadeducida de CD-Bonn se introduceteniendo en cuenta el efectomonopolarnuclear en estaregión de masa. Los resultados se comparanluego con los datosexperimentales disponibles.
Palabras-clave: estructura nuclear; estroncio 100; monopolos; códigos 0; desintegración beta positiva; isótopos deficientes en neutrones
INTRODUCTION
The study of the nuclei with few hole protons and particle neutrons near the heaviest nucleus 100Sn (N=Z) was the main of several theoretical and experimental works that aimed to give a global description of nuclear structure. These isobars are some of the best candidates for giving us opportunity to develop our understanding of nuclear structure due to the proximity of the magic numbers, the proton drip-line and the end of the rp-process.One of the most interesting aspects of the proton-rich nuclei is show in some of the unusual features of their Gamow-Teller beta decays. Very scarce experimental informationin this region are available [1]. The nuclear shape changes rapidly in this region and gives rise to long-lived isomers with small excitation energies [2,3]. With the development of advanced experimental tools such as isotope-separation on-line (ISOL) and in-beam spectroscopy with large
γ
-arrays including ancillary particle detectors and by exploiting spallation and heavy ion induced fusion-evaporation reactions,many of the nuclei along the Z, N = 48-50 isotonic and isotopic chains were be produced with relatively high rates [2,4,5]. Investigations of testing effective interaction, exploring the evolution of the shell structure and beta decays have been performed in some works [3,6-10].
The present analysis deals with three neutron-deficient nuclei 100In, 100Cd and 100Ag neighbours of 100Sn core. Shell model calculations are been performed in the full model space that include the proton and neutron orbits below and above the closed shells Z= N = 50 respectively. This model space enables one to reproduce the shape of the GT strength distribution. In these nuclei, protonspartly fill the g9/2 orbit and the spin-flip transformation
π
g9/2 → vg7/2 allowed by Pauli principle forms the Gamow-Teller (GT+) states in the daughter nucleus. The main part of the strength turns out to lie within the QEC window, thus becoming accessible to the β+ decay [10].
The shell model calculations of the hole-particlemultiplets in these nuclei were performed with code OXBASH [11] supplementing available experimental data.
THEORETICAL FRAMEWORK
Nowadays, studies of radioactive decays are an integral part of investigations atomic nucleus in order to better understand the physical phenomena governing its behavior. The β decay process plays a major role in determining fundamental quantities such as the period, the mass or the energy of the excited levels helping to understand nuclear interaction and the characterization of populated states. Beta decay is a weak interaction process mediated by the well understood
τ
and
σ
τ
operators that govern the observed Fermi (F) and Gamow-Teller (GT) transitions, respectively. Under some experimental conditions, Charge Exchange (CE) reactions proceed by F and GT transitions, although mediated by the strong interaction. Consequently,
β
decay and CE processes can be very similar. The main advantage is that
β
decay provides absolute B(GT) strength values, whilst the CE reactions extend our knowledge to excitation energy regions above the Qβ value. Also, CE reactions can only be studied readily on stable target nuclei, whereas by definition
β
decay is from unstable nuclei. Beta decays of nuclei “southeast" of 100Sn are characterized by large decay energies (QEC) and pure Gamow-Teller (GT) transitions transforming a g9/2 proton to a g7/2 neutron. These features make studies of these decays especially important to test the nuclear shell model in general and its predictions of the GT strength in particular. The experimentally derived quantity which can be directly compared to the theoretical predictions, is the
β
strength function. Gamow-Teller beta-decay strengths provide relatively clear information about the structure of nuclear wave functions because the associated operators are simple and selective, coupling only a few single-nucleon orbits to each other. In addition, these operators do not couple to the first-order admixtures of "excluded" configurations into the "active" space [12].
The theoretically predicted GT strength is defined as the squared matrix element of the free
σ
τ
operator acting between the wave functions of the initial │i>and the final │f> states:
B(GT)=gA22Ji+1|〈f|GT^|i〉|2
(1)
GT±^=∑nσ^τ^±
The factor
gA=1.26
is the axial-vector coupling constant of the weak interaction and Ji is the angular momentum of the initial state.
The quantity ft1/2 value of an allowed beta-decay transition isrelated to Gamow-Teller force B(GT) (1). f is a phase-space integral that contains the lepton kinematics [13] and t1/2 is the half-life.
The focus on the evolution of shell structure in nuclei was increased, in order to understand the appearance of new magic numbers. The effect of the addition of nucleons on the single particle states can lead tospectroscopic properties nuclei that the realistic interactions derived from the N-N force fail to reproduce. The interactions between the supposed inert core and the adding nucleons were be solved by the consideration of the monopole effect introduced by Poves and Zuker [14]. Those were assumed to need drastic revisions of the realistic two-body potentials and proposed to separate the Hamiltonian of the system into two parts:
H=Hm+HM
(2)
where HM denote the multipolepart of the Hamiltonian and
Hm
the monopole one.
Hm
is expressed in term of the average energies over the configurations of s and t orbits with T = 1 for proton-proton and neutron-neutron, and T = 0; 1 for proton-neutron parts, see [15-16] for more details.
VstT=∑J(2J+1)〈jsjt|Vst|jsjt〉JT[1−(−1)J+Tδst]∑J(2J+1)[1−(−1)J+Tδst]
(3)
The two body matrix element
〈jsjt|Vst|jsjt〉J
arisen from the interaction between the particles in the orbits s and t. Itcan be extracted from the proton and/or the neutron separating energies of neighbouring nuclei [17]. The
VstT
(3) defined the diagonal 2b part of the monopole Hamiltonianis associated to a function of the average two body matrix elements (TBMEs).
The main aim of this paper is to present some calculations on nuclear properties of 100In, 100Cd and 100Ag isobars, focusing attention on the levels schemes and the
β
+ decay properties. This study isrealized in the framework of the nuclear shell model by means of Oxbash nuclear structure code [11].
SPECTROSCOPIC CALCULATIONS AND DISCUSSION
We have used the 100Sn core and the full model space where proton holes are allowed to occupy the
π
(0f5/2
-1, 1p3/2
-1, 1p1/2
-1 and0g9/2
-1
)
Z-28orbitals and the neutron particles occupy the v(0g7/2, 1d5/2, 1d3/2,2s1/2 and 1h11/2) N-50 orbitals.The experimental single particle energy (pSHE and nSPE) values are takenfrom 99In for protons and 101Sn for neutrons [18], respectively.
Considered the dependence mass factor (78/100)0.3, the two body matrix elements (TBMEs) of the original interaction jj45apn from
78
Ni mass region [19,20] are scaled. The resulting TBMEs are used in order to calculate the monopole terms. Therefore
V1g9/22d5/20≈−430 keV
;
V1g9/21g9/21≈−110 keV
and
V2d5/22d5/21≈−20 keV
are used to modify
πυ(1g9/22d5/2)J=2,7T=0
;
ππ(1g9/21g9/2)J=0,8T=1
;
υυ(2d5/22d5/2)J=0,4T=1
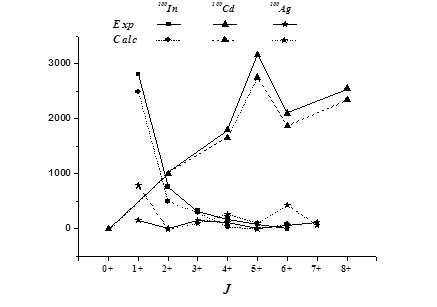
TBMEs, respectively. These TBMEs are chosen basing on the energetic sequence of the single particle space. Using thenew interaction jj45m, some calculations are carried out in order to reproduce the nuclear properties of the three A=100 isobars cited above. The obtained levels schemes are showing on figure 1. The jj45m interaction reproduce the sequence of levels for even-even 100Cd nucleus. A good agreement between calculated energies and experiment ones are observed. This interaction cannot reproduce the spin of the experimental ground state for 100In(6+) and 100Ag(5+) isobars, it gives 5+ and 2+ for this state, respectively. Also, it can’t reproduce the sequence of levels for 100Ag nucleus.
We concentrate on some Gamow-Teller(GT)
β
+ decayproperties between the states (
Δ
J =1) of these nucleiin the vicinity of 100Sn, from (6+) of 100In to (7+ or 5+) of 100Cd and from (0+) of 100Cd to (1+) of 100Ag.
We have evaluated B(GT+) strengths (Figure 2), half-lives (Table 1) and theoretical occupancy changes (Figure 3) related to the
β
decays of 100In into 100Cd and 100In into 100Ag, with the standard quenching factor of 0.77 for
σ
τ
operator measuring the occupancy of the active particles (model space) in the exact wavefunctions.
The shape of the GT strength distribution (fig. 2(a)) up 9400 keV of excitation energyin 100Cd is located in a large QE.C window (9880 keV value) and presented a broad symmetric peak centered around 6 MeV. In addition, a small peak at about 9 MeVcan be seen. The calculations were performed over thirty states. Then, the complete distribution of B(GT) up 3586 keV of excitation energy of the (1+) first ten states in 100Ag is located in two narrow peaks centered at about 800 and 2800 MeV and limited by 3963 keV QE.C.small value.The total GT strengths 8.64 and 9.93are practically the same in both decays.While, the experimental value of 100In is 3.9(9) [10]. But, the calculated T1/2 values are far from the experiment onesby a factor ten.
Table l T1/2 β+ decay calculated of 100In and 100Cd nuclei andthe experimental ones
| Nucleus |
T1/2 (s) Exp |
T1/2 (s) Cal |
Q
β+
(MeV) |
∑B(GT)
|
|
100
In
|
5,8 ± 0,2 |
0,57 |
8,86 |
8,64061 |
|
100
Cd
|
49,1 ± 0,5 |
2,61 |
2,921 |
9,9277 |
Figure 3 shows that theoretical occupancy changes (with
Δ
J =1) of valence nucleons in the states of parent and daughter nuclei are maximum of proton hole-1g9/2 and neutron particle-1g7/2 orbitals respectively. A small contribution of the proton orbitals 2p3/2 and 2p1/2 is obtained in the case of 100Cd decay. The GT decay towards 100Cd will populate the two quasi particle (2qp) configuration vg7/2².
SUMMARY
This study is based on the energetic spectra and Gamow-Teller
β
+ decay properties calculations for nuclei near 100Sn, with few hole protons and particle neutrons in their valence spaces. The calculations are realized in the framework of the nuclear shell model, by means of Oxbash nuclear structure code. Using the jj45apn original interaction of the code, we carried out some modifications based on the monopole effect to get jj45m new interaction.This interaction reproduce the energetic spectrum for 100Cd nucleus, it can’t reproduce theground statefor odd-odd 100In and 100Ag isobars and the sequence of levels for 100Ag nucleus.The complete distributions of B(GT) strengths of excitation states in daughter nuclei are located in centered peaks and limited by QE.C. values.Their values are practically the same in both decaysand different from experimental value for100In. The calculated T1/2 valuesobtained with the standard quenching factor of 0.77 for
σ
τ
operator related to the
β
+ decay of 100In and 100Cd are far from the experiment ones by a factor tenand depend substantially on the model used.
Acknowledgement
Authors would like to thank the organizers of LASNPA&WONP-NURT 2017 for the organization and the support provided during the symposium.
Special thanks are owed to B. A. Brown, for his help in providing us the Oxbash code (Windows Version), and to M. H. Jensen, for the documents and the information provided about the interaction jj45apn.
References
1.
[1] KANKAINEN A, NOVIKOS YuN, SCHATZ H & WEBER C. Mass measurements of neutron-deficient nuclei and their implications for astrophysics. Eur. Phys. J. A. 2012; 48: 50-69. [ Links ]
2.
[2] BLOCK M, ACKERMANN D, BLAUM K, CHAUDHURI A, et. al. Mass measurements in the endpoint region of the rp-process at SHIPTRAP. Hyperfine Interact. 2006; 173: 133-142. [ Links ]
3.
[3] BATIST L, GORSKA M, GRAWE H, JANAS Z, et. al. Systematics of Gamow-Teller beta decay “Southeast” of 1003.
Sn. Eur. Phys. J. A . 2010; 46: 45-53. [ Links ]
4.
[4] FAESTERMANN T, GORSKA M , GRAWE H. The structure of 1004.
Sn and neighbouring nuclei. Progress in Part. And Nuc. Phys. 2013; 69: 85-130. [ Links ]
5.
[5] GIERLIK M, PLOCHOCKI A, KARNY M, URBAN Z, et. al. Gamow-Teller strength distribution near 1005.
Sn. The beta decay of 1025.
In. Nuc. Phys. A. 2003; 724: 313-332. [ Links ]
6.
[6] CORRAGIO L, COVELLO A, GARGANO A, AND ITACO N. Structure of particle-hole around 1006.
Sn. Phys. Rev. C. 2004; 70: 034310. [ Links ]
7.
[7] BROWN BA, AND RYKACZEWSKI K. Gamow-Tellar strength in the region of 1007.
Sn. Phys. Rev. C . 1994; 50(5): R2270-R2273. [ Links ]
8.
[8] KARNY M , BATIST L , BANU A, BECKER F, et. al. Beta decay of the proton-rich nuclei 1028.
Sn and 1048.
Sn. Eur. Phys. J. A . 2006; 27: 129-136. [ Links ]
9.
[9] HINKE CB, BOHMER M, BOUTACHKOV P, FAESTERMANN T , et. al. Superallowed Gamow-Teller decay of the doubly magic nucleus 1009.
Sn. Nature. 2012; 486:341-345. [ Links ]
10.
[10] PLETTNER C, BATIST L , ORING J, BLAZHEV A, et. al. <math> <mi>β</mi></math> decay of 10010.
In. Phys. Rev. C . 2002; 66: 044319. [ Links ]
11.
[11] BROWN BA . Oxbash for Windows. MSU-NSCL Report 1289. 2004. [ Links ]
12.
[12] BROWN BA & WILDENTHAL BH. Status of the nuclear shell model. Ann. Rev. Nucl. Part. Sci. 1988; 38: 29-66. [ Links ]
13.
[13] SUHONEN J. Theoretical and mathematical physics from nucleons to nucleus. Springer, 2007. [ Links ]
14.
[14] POVES A & ZUKER AP. Theoretical spectroscopy and the fp shell. Phys. Rep. 1981; 70(4): 235-314. [ Links ]
15.
[15] ZUKER AP . Three-body monopole corrections to realistic interactions. Phys. Rev. Lett. 2003; 90(4): 042502. [ Links ]
16.
[16] ZUKER AP. Shell formation and three-body forces. Int. J. Modern Phys. E. 2004; 13: 53-61. [ Links ]
17.
[17] SORLIN O & PORQUET MG. Nuclear magic numbers: new features far from stability. Prog. Part. Nucl. Phys. 2008; 61: 602-673. [ Links ]
18.
[18] GRAWE H , LANGANKE K & MARTINEZ-PINEDO G. Nuclear structure and astrophysics. Rep. Prog. Phys. 2007; 70: 1525-1582. [ Links ]
19.
[19] HJORTH-JENSEN M, KUO TTS & OSNES E. Realistic effective interactions for nuclear systems. Phys. Rep. 1995; 261: 125-270. [ Links ]
20.
[20] REJMUND M, NAVIN A, BHATTACHARYYA S, CAAMANO M, et. al. Structural changes at large angular momentum in neutron-rich 121,12320.
Cd. Phys. Rev. C . 2016; 93: 024312. [ Links ]
21.
[21] National Nuclear Data Center (NNDC). Disponible en: http://www.nndc.bnl.gov21.
. [ Links ]