My SciELO
Services on Demand
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
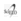 Similars in
SciELO
Similars in
SciELO
Share
Ingeniería Hidráulica y Ambiental
Print version ISSN 1680-0338
riha vol.38 no.1 La Habana Jan.-Apr. 2017
ARTÍCULO ORIGINAL
Cinética de la remoción de DBO5 en humedales con flujo sub-superficial horizontal
Kinetics of BOD5 removal in constructed wetlands with horizontal subsurface flow
Josué Bernardo Larriva Vásquez,I Orestes Arsenio González Díaz,II
I ETAPA EP, Empresa de telecomunicaciones, agua potable y saneamiento de Cuenca, Ecuador.
II Centro de Investigaciones Hidráulicas (CIH). Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae). Habana.
RESUMEN
En el presente trabajo se presentan los estudios realizados en humedales artificiales de flujo sub-superficial horizontal para el tratamiento de aguas residuales en los Andes Ecuatorianos, usando diferentes tiempos de retención hidráulica y diferentes plantas emergentes. La aplicación de los modelos de flujo disperso y tanques en serie para el estudio de la remoción de la Demanda Bioquímica de Oxigeno con esta tecnología mostró la importancia de incluir los elementos geométricos e hidráulicos de los reactores en las metodologías de diseño de humedales de flujo sub-superficial horizontal.
Palabras clave: humedales artificiales, modelo de flujo disperso, modelo de flujo pistón, modelo de tanques en serie, remoción de DBO5.
ABSTRACT
In the present work, studies are presented about horizontal subsurface flow in constructed wetlands for wastewater treatment in the Ecuatorian Andes, using different hydraulic retention times and different emerging plants. The application of the dispersion axial models and series tanks model to study the removal of Biochemical Oxygen Demand shows the importance of including geometric and hydraulic elements of the reactors in the design methodologies for horizontal subsurface flow in constructed wetlands.
Key words: constructed wetlands, dispersion axial model, plug flow model, series tank model, BOD5 removal.
INTRODUCCIÓN
Los tratamientos llamados no convencionales o tecnologías blandas se muestran como una alternativa para la depuración de las aguas residuales para comunidades pequeñas o sistemas rurales, ya que no son costosos ni requieren altos consumos energéticos, además de que su operación y mantenimiento no requieren de personal especializado ni procesos complicados.
A nivel mundial se ha extendido cada vez más el uso de los humedales artificiales o wetlands, los cuales funcionan a partir de los mecanismos propios que usa la naturaleza para la depuración de las aguas residuales, en donde se combinan procesos físicos, químicos y biológicos entre el suelo, las plantas, los microorganismos y la atmósfera, dando lugar a la ocurrencia de procesos de sedimentación, filtración, absorción, degradación biológica, fotosíntesis, foto-oxidación y toma de nutrientes por parte de la vegetación mediante el metabolismo (González 2011).
Existen 2 tipos de humedales artificiales, de acuerdo con el tipo de flujo: los de flujo superficial, en los que el agua fluye expuesta a la atmósfera, y los de flujo sub-superficial, en los que el agua fluye a través de un material de soporte, generalmente grava.
De estos últimos a partir de la última década se los distingue entre los de flujo vertical y los de flujo horizontal, debido a que el funcionamiento hidráulico difiere entre uno u otro (Stefanakis et al. 2014). Estudios publicados sobre experiencias en Latinoamérica demuestran la capacidad de los humedales de flujo sub-superficial para remover cantidades significativas de materia orgánica, nitrógeno, fósforo, sólidos suspendidos, bacterias y metales pesados del agua residual (Rivas y Paredes 2014).
Sin embargo, para la adaptación de cualquier tecnología a las condiciones de un lugar se requiere de estudios que conduzcan a la obtención de coeficientes propios de diseño o adaptaciones a la metodología de diseño utilizada en lugares en donde estos procesos ya han sido estudiados. En los últimos años ya se reportan, en Latinoamérica, experiencias de valoración del funcionamiento de este tipo de tecnología para las condiciones propias de cada lugar, o con variaciones en el tipo de vegetación, o material de soporte (Díaz y Romero 2013).
Con estos antecedentes y con el fin de encontrar parámetros de diseño, en cuanto a remoción de carga orgánica, para el uso de humedales artificiales de flujo sub-superficial en el tratamiento de aguas residuales para las condiciones de los sistemas rurales ubicados en los Andes Ecuatorianos de la provincia del Azuay, se realizaron pruebas tanto hidráulicas como biológicas en reactores prototipo, con el fin de encontrar el modelo que mejor represente el funcionamiento de dichos reactores y las constantes cinéticas para remoción de DBO5 de dichos reactores.
Finalmente se indica que las poblaciones, hacia quienes van enfocados los estudios, se asientan sobre los 2.500 m.s.n.m., el clima durante el año va de templado a frío y por las condiciones de funcionamiento del sistema de alcantarillado, cuentan con cargas orgánicas bajas debido a que los sistemas de recolección son de tipo combinado, y por tanto requieren de tiempos de retención hidráulica mayores para llegar a eficiencias altas.
MODELOS APLICABLES A LA REMOCION DE DBO5 EN HUMEDALES ARTIFICIALES DE FLUJO SUB-SUPRFICIAL HORIZONTAL.
Modelo de flujo pistón
Los principales criterios de diseño usados para el dimensionamiento de este tipo de humedales son: la profundidad de los mismos, en función de la vegetación emergente a utilizar, el área de la sección transversal, para lo cual es muy importante la conductividad hidráulica del material de soporte (Kadlec and Wallace 2009), y el área superficial a utilizarse, que es sin duda el parámetro más importante, ya que la mayoría de las metodologías modernas de diseño se basan en limitar la carga orgánica y la carga hidráulica por unidad de área que debe aplicarse a un humedal artificial para lograr efluentes de 20 mg/L de DBO y 30 mg/L de SS, de acuerdo con las normas de vertimiento a cuerpos receptores en cada país, y que para el Ecuador se describen en el «Texto Unificado de Legislación Ambiental: Norma de calidad ambiental y de descarga de efluentes recurso Agua» .
De acuerdo con lo planteado en la EPA (2000), se recomienda la siguiente ecuación (1) para el cálculo del área superficial en Humedales de flujo sub-superficial horizontal.
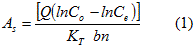
Esta se deriva del modelo aplicado para flujo pistón, que relaciona la eficiencia de remoción con el tiempo de retención, ecuación (2).
![]()
donde:
Ce: concentración de DBO5 del efluente (mg/L)
Co: concentración de DBO5 del afluente (mg/L)
KT: constante de velocidad de reacción del sistema (d-1)
θ: es el tiempo de retención (d)
b: es la profundidad del lecho (m)
n: es la porosidad del medio (como fracción)
As: es el área superficial del sistema (m2)
De acuerdo con este método el valor de KT de cada sistema depende de la temperatura (T en oC), recomendándose para el cálculo la siguiente ecuación (3).
![]()
Para la cual K20 es la constante de velocidad de reacción del sistema a 20oC y tiene el valor de 1,104 d-1. Esta formulación, para condiciones de flujo pistón, supone una cinética de primer orden, condiciones estables y falta de perdidas debido a la evapotranspiración y la infiltración, sin embargo consideran condiciones de flujo teóricas, las cuales no se cumplen por completo en la práctica. Estudios presentados respecto al funcionamiento hidráulico de los humedales artificiales (González 2014) indican que los mismos no operan como reactores 100% de flujo pistón, y por tanto podrían aplicarse otros métodos que consideren las condiciones reales del flujo.
Modelo de flujo disperso
El modelo de flujo disperso describe el transporte de un contaminante en un reactor tipo alargado, el cual está afectado por la dispersión convectiva en la dirección del flujo y por la dispersión molecular axial en el sentido transversal. La ecuación general de este modelo es la ecuación (4).
![]()
donde:
C: concentración del contaminante (mg/L)
X: coordenada en la dirección del flujo (m)
U: velocidad longitudinal promedio del reactor (m/día)
D: coeficiente de dispersión longitudinal o axial (m2/día)
t: tiempo (d)
KT: constante de velocidad de reacción del sistema (d-1)
En la ecuación anterior el primer término de la derecha es la dispersión por difusión molecular, en la práctica se usa el término dispersión, y el segundo término es la dispersión convectiva, llamado también transporte convectivo y el tercero es el decaimiento del contaminante. La ecuación anterior es conocida como modelo de flujo pistón con dispersión axial o modelo de flujo disperso.
La solución a la ecuación diferencial anterior (Sáenz 1987) fue desarrollada por Wehner y Wilhem con el criterio de continuidad en la entrada y salida del reactor, ubicando adecuadamente el sub-modelo hidráulico de un reactor entre los límites de mezcla completa y flujo tipo pistón. Esta solución se expresa en las siguientes ecuaciones (5) y (6).
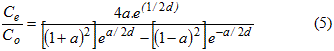
![]()
En donde: d es el valor de la dispersión, que puede ser evaluada en función de las características geométricas del reactor y θ el tiempo de retención hidráulica. Este modelo es usado para diseñar otros sistemas naturales como el lagunaje, ya que representa de mejor manera el fenómeno que ocurre dentro de este tipo de reactores. Para los sistemas de humedales artificiales de flujo sub-superficial, el valor de d puede valorarse (González 2011) con la siguiente ecuación (7).
![]()
donde:
R: radio hidráulico del canal equivalente = 2h+b (m).
h: altura del agua (m).
b: ancho (m).
L: longitud (m).
u: velocidad aparente del flujo (m/s).
KD: conductividad hidráulica Darciana (m/s).
d: coeficiente de dispersión
Modelo de tanques en serie
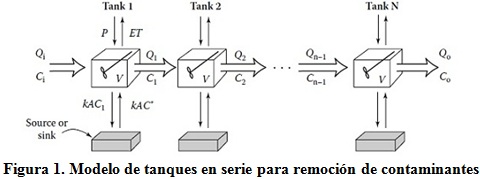
El modelo de tanques en serie supone que el reactor puede representarse dividido en varios tanques de mezcla completa ideal, del mismo tamaño y en serie, siendo la cantidad de tanques el único parámetro a determinar en la valoración hidráulica del reactor (Levenspiel 1997). La ecuación (8) de la curva adimensional C para N tanques en serie tiene la siguiente forma:
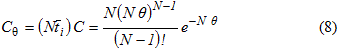
Siendo: t-i: tiempo medio de residencia por cada tanque; t- = Nt-i tiempo medio de residencia en el conjunto de N tanques; θi = t / t-i = N t / t- y θ = t / t- = t / Nt-i . Obsérvese que, lógicamente, mientras mayor es N más se acerca el comportamiento al flujo pistón. El valor del parámetro N puede calcularse mediante la varianza de la curva C, y la representación gráfica de la cinética del proceso puede verse en la figura 1 (Kadlec and Wallace 2009).
El agua pasa a través de N tanques en serie y disminuye la concentración del contaminante en cada uno. Para el caso en que no existan pérdidas o ganancias de agua, y considerando una constante de remoción KN que no varía con el tiempo de residencia en el humedal, la concentración del contaminante en el tanque j es:
![]()
donde:
Cj: concentración de DBO5 en el tanque j (mg/L)
Para la secuencia de N tanques, y siendo q=Q/A, el balance de masas es el siguiente:
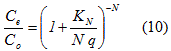
donde:
KN: constante de reacción de primer orden base área para N tanques en serie (m/año)
N: es el número de tanques de mezcla completa en serie supuesto.
q: es la carga hidráulica por unidad de área (m/año).
Adicionalmente se debe indicar que la expresión (2) es un modelo de reacción base volumen, mientras que al utilizar la valoración del número de tanques en serie, como se puede ver, pueden aplicarse modelos de reacción base área y cargas hidráulicas para el análisis de estos reactores (Kadlec and Wallace 2009). Este modelo, según estos investigadores, es el que mejor representa el comportamiento del flujo en humedales artificiales de flujo sub-superficial horizontal. Los términos KT θ de la expresión (2) y KN /q de la expresión (10) son conocidos como el número de Damköhler (Da), para los modelos base volumen y base área respectivamente.
MATERIALES Y METODOS
Para el desarrollo de este trabajo se utilizaron las instalaciones de la planta de tratamiento de aguas residuales de Ucubamba pertenecientes a la Empresa ETAPA EP de la ciudad de Cuenca, Ecuador, ubicando los pilotos junto a la salida del desarenador de la planta desde donde se alimenta a los mismos.
Se utilizaron tres reactores (tanques de acero inoxidable) de sección transversal trapezoidal de 2,80 m de largo, 0,60 m de profundidad, 1,30 m de ancho superior y 1,20 m de ancho inferior como se muestra en la figura 2. Como material de soporte se utilizó grava de 18 a 25 mm, con una porosidad del 38% hasta una altura de 0,45 m. Su colocación fue aleatoria ocupando un volumen efectivo de aproximadamente 0,60 m3.
Se colocaron pozos de muestreo en el primer y segundo tercio del reactor con el fin de evaluar también estos puntos, los que están colocados de forma vertical, desde el fondo del reactor hasta 0,05 m por encima de la grava, en el medio soporte. Consisten en 4 tubos de 150 mm de diámetro y 0,65 m de longitud perforados en toda su área lateral para permitir que el flujo pase a través de ellos sin que se originen perturbaciones. Están espaciados a 1 m y separados 0,90 m de la entrada y salida en sentido longitudinal, con el objetivo de obtener mediciones por tercios del reactor. Los pozos están espaciados a 0,60 m y separados 0,40 m de los laterales en la parte superior del reactor en sentido transversal, con el fin de evitar la influencia de las condiciones de contorno.
Los reactores fueron diseñados considerando una pendiente de 1% (EPA 2000) para garantizar un gradiente hidráulico suficiente. Como estructura de entrada se colocó piedra de 18 a 25 cm de diámetro para evitar obstrucciones en el sistema y sobre esta zona se colocó un tubo de PVC de 25 mm de diámetro perforado con 10 agujeros de 9 mm de diámetro a cada lado. Adicionalmente como estructura de entrada se colocó un baffle de acero inoxidable en los 30 centímetros superiores del área de entrada lo que obliga a que el agua salga por la parte inferior y así minimizar las zonas muertas. Para recoger el agua se utilizó otro tubo de PVC de 50 mm de diámetro perforado con 10 agujeros de 9 mm de diámetro, precedido así mismo de otro baffle de acero inoxidable mediante el cual se asegura la utilización de todo el volumen del reactor. En la figura 3 se pueden observar las estructuras de entrada y salida. El efluente de los tres reactores se vierte hacia el drenaje de la planta de tratamiento.
En la figura 4 se observa la vegetación emergente, uno de los tanques funcionó sin plantas mientras que en los otros dos se usaron variedades de Totora (Scirpus californicus) y Carrizo (Phragmities australis) propias de la sierra ecuatoriana, y se utilizó la recomendación de la EPA (2000) de 4 plantas por m2 para la ubicación de las plantas.
Para la toma de muestras se utilizaron 3 equipos automáticos para muestras compuestas, el intervalo de muestras fue de 1 hora y puede verse uno de los equipos en la figura 3. Se realizaron 16 pruebas para cada uno de los reactores, 3 pruebas con muestras compuestas para cada uno de los 5 tiempos de retención hidráulica ensayados y una muestra puntual adicional al final del experimento. La toma de muestras se realizó en la semana posterior a estabilizar cada uno de los tiempos de retención ensayados. El método para determinar la DBO5 fue el Standard Methods 5220 D, en el laboratorio de la planta de Ucubamba, el cual está acreditado desde el año 2005 por el OAE, organismo ecuatoriano competente para realizar esta prueba.
Para el material de soporte se realizaron las pruebas de granulometría, peso específico, porosidad y valoración de la conductividad hidráulica, previo a la realización de pruebas de trazadores para tiempos de retención hidráulica de 24 y 36 horas. Al tabularse los resultados obtenidos se encontraron los valores del coeficiente de dispersión d de la ecuación (6) para las pruebas realizadas. Si se consideran los términos que intervienen en (6) se puede observar que si se realizan diferentes pruebas en un mismo reactor, para el cual no cambian las características geométricas (b, L, h, R), ni las del medio de soporte (KD), y tampoco las de las condiciones ambientales (temperatura) la variación del valor del coeficiente de dispersión dependerá de la variación de la velocidad aparente del flujo afectada por el coeficiente 0,386.
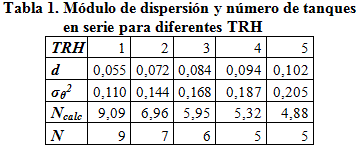
Con este criterio, y sabiendo que la velocidad aparente en el reactor varia proporcionalmente al tiempo de retención hidráulica (TRH), se calcularon los valores de d para los diferentes TRH con los que iban a realizarse las pruebas, con el fin de usar dicho valor en el ajuste por el modelo de flujo disperso. Adicionalmente en función de d pueden calcularse el valor de la varianza dimensional (σθ2) y el número teórico de tanques en serie, para el ajuste por este método. Finalmente se muestra el valor entero asumido de N para el ajuste por el modelo de tanques en serie más adelante en el apartado de resultados. Los valores obtenidos se muestran en la tabla 1.
RESULTADOS Y DISCUSIÓN
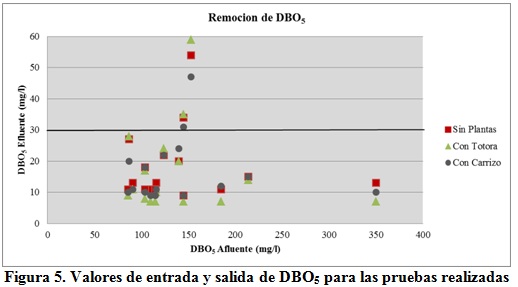
Se realizaron 16 pruebas entre marzo y septiembre del 2014 para tiempos de retención hidráulica de 1 a 5 días y para los 3 reactores. Dichos valores representados por los puntos entrada/salida de DBO5 se muestran gráficamente en la figura 5.
Como se puede observar en la figura 5, el uso de esta tecnología da muy buenos resultados, en el gráfico se comparan todos los resultados obtenidos con el valor de 30 mg/L, valor de descarga ampliamente utilizado en normativas internacionales, observándose que la mayoría de los casos cumplirían con ese límite.
Eficiencia en la remoción en función del TRH
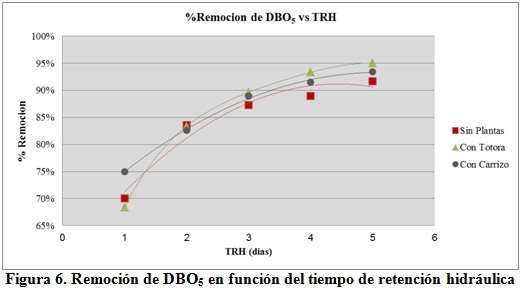
En la figura 6 se muestra los valores promedios de las remociones alcanzadas, expresadas como porcentaje, para diferentes TRH en los tres reactores utilizados.
Al analizar la eficiencia de remoción de DBO5 contra el TRH se puede observar que es necesario entre 3,5 y 4 días para asegurar eficiencias del 90%, valores que son comparables a las experiencias reportadas por la bibliografía (Vymazal and Kröpfelová 2008, Maltby and Barker 2009) y que son mayores que los que pueden obtenerse en zonas de clima cálido como en la costa ecuatoriana o países tropicales. Por otra parte el reactor con Totora es el que mayor eficacia alcanza, y en general los humedales con plantas obtienen entre 2 y 6 % mayor remoción que el que no tiene plantas para TRH entre 3 y 5 días.
Eficiencia en la remoción en función de la distancia
En las pruebas realizadas se tomaron datos en el primer y segundo tercio de cada reactor, además de en la salida del mismo, con el fin de valorar la remoción de DBO5 a lo largo de los reactores. En la figura 7 aparecen representados los porcentajes promedios de remoción contra distancia para los TRH de 3 y 5 días, observándose que, de manera similar a lo mostrado en la figura 5, los reactores con plantas son más eficientes que el que no las tiene. Adicionalmente se puede señalar que el reactor con Totora tiene siempre mejores resultados. Este fenómeno se debe a que esta planta es la que se encuentra en los pantanos naturales de la zona en la que se realizaron las pruebas, con lo que se concluye que para lograr un buen funcionamiento es necesario el uso de plantas propias de cada región. Los resultados obtenidos muestran que el mayor porcentaje de eliminación ocurre en el primer tercio del reactor, para cualquier TRH.
Análisis con el modelo de flujo pistón
Con el fin de determinar cuál es la constante de velocidad de reacción del sistema KT, de acuerdo con el modelo de flujo pistón, se realizaron los gráficos que se muestran en la figura 8, los cuales muestran las eficiencias obtenidas en términos de Ce/Co contra el TRH de las pruebas realizadas y una gráfica de ajuste dibujada de manera manual. Adicionalmente se ha graficado en azul el ajuste mediante este modelo.
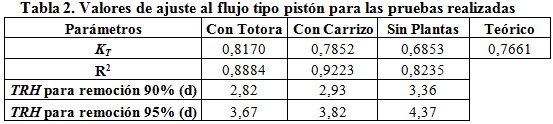
En la tabla 2 se muestran los valores de KT, de la ecuación (2), para cada reactor y se compara contra el valor, en función de la temperatura media (14,64oC) de los ensayos, recomendado por la ecuación (3). Los valores R2 de ajuste a este modelo pueden considerarse buenos y los valores obtenidos de KT para los tres reactores, en comparación con el valor propuesto por la ecuación (3), guardan cierta correspondencia. Sin embargo comparando los resultados entre ellos se puede observar una diferencia significativa entre las constantes obtenidas.
Además, al tratar de proyectar valores usando este ajuste para obtener, por ejemplo, una remoción del 90% o 95% de DBO5, se obtienen tiempos inferiores a los observados y como se ve en los gráficos de la figura 8 este modelo tiende a sobreestimar los resultados para valores de TRH mayores que 3 días.
Análisis con el modelo de flujo disperso
En la figura 9, al igual que en el acápite anterior, se muestra el ajuste de los valores de las eficiencias de remoción en términos de Ce/Co contra TRH, con la diferencia de que en azul se muestran los valores de ajuste obtenidos por el modelo de flujo disperso.
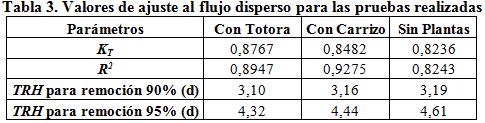
En la tabla 3 se muestran los valores de ajuste a las ecuaciones (5) y (6) del flujo disperso, incluyendo además los tiempos proyectados por este método para una remoción del 90% o 95% de DBO5. Para el ajuste de la ecuación se consideró los valores de la dispersión y tiempos de retención hidráulica que constan en la tabla 1 y los valores de KT se obtuvieron por el método de ajuste por mínimos cuadrados.
Los valores R2 de ajuste obtenido por este modelo son mejores que los obtenidos por el modelo de flujo pistón y además se puede observar que las constantes de reducción KT obtenidas, si bien muestran que los reactores con plantas son más eficientes, los valores tienen un orden de magnitud muy parecido, de manera similar con los resultados obtenidos. Por otro lado, al realizar el mismo ejercicio de calcular ´por este método el número de días necesarios para una disminución de un 90% y 95% de la DBO, se obtuvieron valores semejantes a los observados, y en general un mejor ajuste, el cual se evidencia en los gráficos de la figura 9.
Análisis con el modelo de tanques en serie
En la figura 10, al igual que en los casos anteriores se muestra el ajuste de los valores de las eficiencias de remoción en términos de Ce/Co contra TRH, en esta ocasión en azul se muestran los valores de ajuste obtenidos por el modelo de tanques en serie.
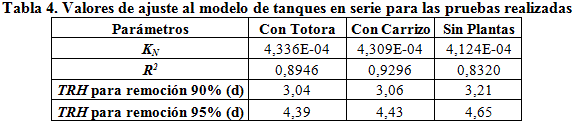
En la tabla 4 se muestran los valores de ajuste a la ecuación (10) del modelo de tanques en serie, incluyendo además los tiempos proyectados por este método para una remoción del 90% o 95% de DBO5. Para el ajuste de la ecuación se consideró los valores del número de tanques en serie y tiempos de retención hidráulica que constan en la tabla 1.
El valor q se calculó en cada caso con el caudal del sistema correspondiente a cada tiempo de retención y dividido para el área útil del humedal y expresado en metros por año. Los valores de KN se obtuvieron por el método de ajuste por mínimos cuadrados.
Los valores R2 de ajuste obtenido son muy similares a los del flujo disperso. De igual forma las constantes de reducción KN obtenidas, muestran el mejor comportamiento de los humedales con plantas pero tienen un orden de magnitud muy parecido, lo que concuerda con los resultados obtenidos. Finalmente al realizar el cálculo por este método del número de días necesarios para una disminución de un 90% y 95% de la DBO, obteniéndose valores semejantes a los observados, de manera similar a lo ocurrido con el análisis con el flujo disperso.
En la tabla 5 se muestran los promedios de los errores absolutos entre los TRH observados y proyectados por los diferentes modelos de ajuste para remociones del 90 y 95% de DBO5. Se puede ver cómo los modelos que consideran la dispersión del flujo representan de mejor forma el comportamiento real de las pruebas realizadas.
Este análisis muestra que el modelo de flujo disperso y el de tanques en serie tienen mejores resultados para el cálculo de la remoción de DBO en humedales de flujo sub-superficial, pues consideran la dispersión del flujo, con la ventaja en el modelo de tanques en serie que incorpora el concepto de carga hidráulica muy utilizado en otros procesos unitarios de plantas de tratamiento.
Se podría decir que cuando la remoción de DBO necesaria, requiere de pocos días, 1 o 2 días, como sucede para climas tropicales, puede ser razonablemente aproximada una relación de flujo a pistón de primer orden. Sin embargo para cuando se requieran TRH mayores o iguales a 3 días, como el caso de los Andes Ecuatorianos, al bajar la velocidad de circulación crece la influencia de la dispersión del flujo y por tanto deben considerarse modelos que incluyan este parámetro. Por esta razón y considerando que el modelo de tanques en serie considera adicionalmente el valor de la carga hidráulica, podría concluirse que este modelo es el que describe, de manera más completa, el comportamiento de este tipo de reactores.
Finalmente, el análisis realizado, evidencia la importancia de considerar en las metodologías de diseño de humedales de flujo sub-superficial horizontal, los factores que influyen en el valor de la dispersión del flujo como son la relación largo/ancho, la profundidad de raíces, la conductividad hidráulica, la temperatura del agua, la velocidad aparente del flujo además de la carga hidráulica, con el fin de valorar de forma más acabada la eficiencia en la remoción de carga orgánica esperada.
CONCLUSIONES
Se muestra, mediante la aplicación de diferentes modelos de flujo a los datos obtenidos en pruebas de funcionamiento biológico en humedales de flujo sub-superficial, que el modelo de tanques en serie es el que mejor representa la remoción de DBO5 para tiempos de retención hidráulica mayores que 3 días en este tipo de tratamientos. La experiencia realizada muestra la validez de usar esta tecnología para el tratamiento de aguas residuales de zonas rurales de los Andes del Ecuador, y se calcularon las constantes cinéticas para remoción de DBO5, que pueden ser utilizadas para el diseño de reactores en condiciones de funcionamiento similares como tiempos de retención hidráulica y cargas superficiales.
De los resultados obtenidos se puede ver la importancia de considerar el funcionamiento hidráulico de un reactor a la hora de valorar su eficiencia en la remoción de contaminantes, y que para obtener resultados similares en escala real, de manera posterior, se debe realizar un correcto diseño hidráulico que considere estructuras de entrada, salida, relaciones largo/ancho, velocidades aparentes de flujo y otros, ya que como se observó el grado de dispersión del flujo incide en los resultados biológicos que puedan obtenerse.
REFERENCIAS BIBLIOGRÁFICAS
1. Díaz C. y Romero J., «Evaluación de la remoción de DBO, DQO, SST, NTK, PT y CF en un humedal de flujo subsuperficial construido con carbón mineral y cultivado con Zantedeschia aethiopica». Revista Escuela Colombiana de Ingeniería, (2013), v. 1 No. 89 pp.29-37 ISSN: 0121-5132. Editorial Escuela Colombiana de Ingeniería, Colombia.
2. EPA «Constructed Weatlands Treatment of Municipal Wastewater». Office of Research and Development, U.S. Enviromental Protection Agency, EPA/625/R-99/010, Cincinnati, Ohio. (2000).
3. González O. «Metodología para el diseño de humedales de flujo sub-superficial» Ingeniería Hidráulica y Ambiental, (2011), vol. 32, no. 1, pp 61-70, ISSN 1815-591X, CIH, Inst. Superior Politécnico José Antonio Echeverría (Cujae), La Habana, Cuba.
4. González O. «Modelación matemática del fenómeno de la dispersión en humedales de flujo sub-superficial horizontal». 17 Convención Científica de Ingeniería y Arquitectura, Inst. Superior Politécnico José Antonio Echeverría (Cujae), La Habana, Cuba. (2014).
5. Kadlec R. H. and Wallace S. «Treatment wetlands». Taylor & Francis Group, ISBN 978-1-56670-526-4, Boca Raton, Florida. (2009)
6. Levenspiel O. «Ingeniería de las reacciones químicas». Editorial Reverté S.A., Sexta edición, ISBN 64291-73250, Barcelona, España. (1997).
7. Maltby E. and Barker T. «The Wetlands Handbook». Editorial John Wiley & Sons, 1 edición, ISBN: 9781444315820, USA. (2009)
8. Rivas A. y Paredes D. «Sistemas de humedales para el manejo, tratamiento y mejoramiento de la calidad del agua: memorias de la Segunda Conferencia Panamericana en Sistemas de Humedales para el Manejo, Tratamiento y Mejoramiento de la Calidad del Agua» Instituto Instituto Mexicano de Tecnología del Agua, ISBN 97895872231909, Morelia, Michoacán, México. (2014)
9. Sáenz R. «Predicción de la calidad de efluentes de lagunas de estabilización». Hoja de divulgación técnica No 3, CEPIS/OPS, Lima, Perú. (1987).
10. Stefanakis A., Akratos C. and Tsihrintzis V. «Vertical Flow Constructed Wetlands: Eco-engineering Systems for Wastewater and Sludge Treatment», Editorial Elsevier Science, primera edición ISBN: 9780124046122, USA. (2014)
11. Vymazal J. and Kröpfelová L. «Wastewater Treatment in Constructed Wetlands with Horizontal Sub-Surface Flow», Editorial Springer Netherlands, primera edición, ISBN: 9781402085796, Holanda. (2008)
Recibido: 3 de octubre de 2015.
Aprobado: 27 de octubre de 2016.
Josué Bernardo Larriva Vásquez, Orestes Arsenio González Díaz. ETAPA EP, Empresa de telecomunicaciones, agua potable y saneamiento de Cuenca, Ecuador. Centro de Investigaciones Hidráulicas (CIH). Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae). Habana. e-mail: jlarriva@etapa.net.ec, e-mail: orestes@cih.cujae.edu.cu